鲁教版(五四制)七上 6.1函数(课件)(39ppt))
文档属性
| 名称 | 鲁教版(五四制)七上 6.1函数(课件)(39ppt)) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-02 14:55:45 | ||
图片预览




文档简介
(共39张PPT)
我们生活在一个变化的世界中,在我们的周围充满着许许多多变化的量。
你能从生活中举出
一些发生变化的
量吗?
你了解这些变量之间的关系吗?
创设情境
温故探新
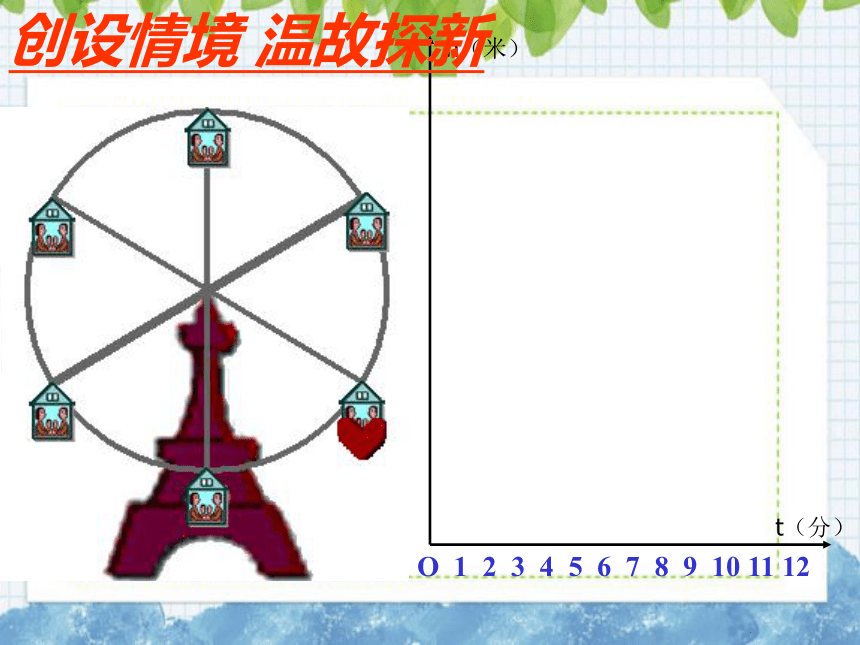
问题一:你坐过摩天轮吗?想一想,如果你坐在摩天轮上时,随着时间的变化,你离开地面的高度是如何变化的?
创设情境
温故探新
O
1
2
3
4
5
6
7
8
9
10
11
12
h(米)
t(分)
创设情境
温故探新
O
1
2
3
4
5
6
7
8
9
10
11
12
3
h(米)
t(分)
创设情境
温故探新
O
1
2
3
4
5
6
7
8
9
10
11
12
3
14
h(米)
t(分)
创设情境
温故探新
O
1
2
3
4
5
6
7
8
9
10
11
12
3
14
36
h(米)
t(分)
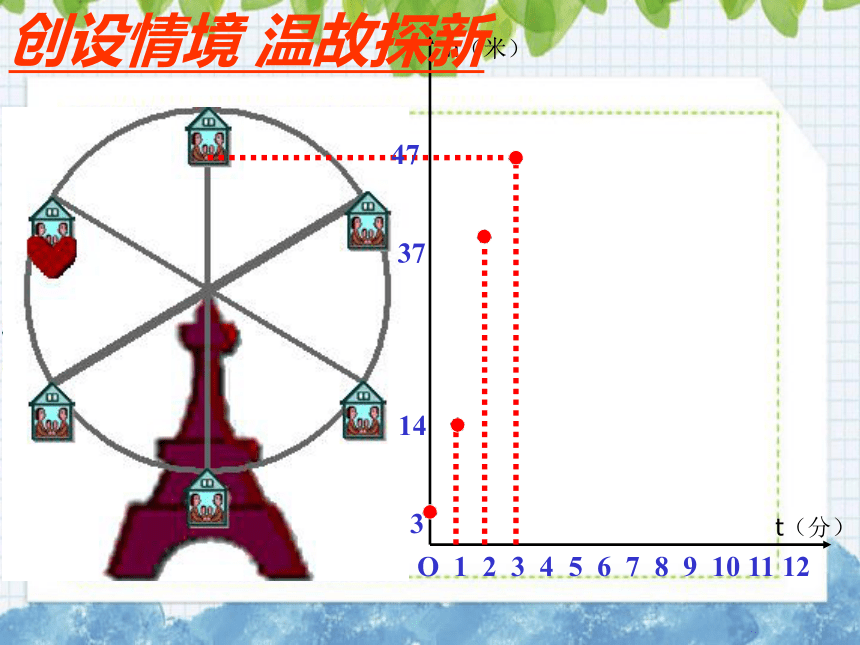
创设情境
温故探新
O
1
2
3
4
5
6
7
8
9
10
11
12
3
14
37
47
h(米)
t(分)
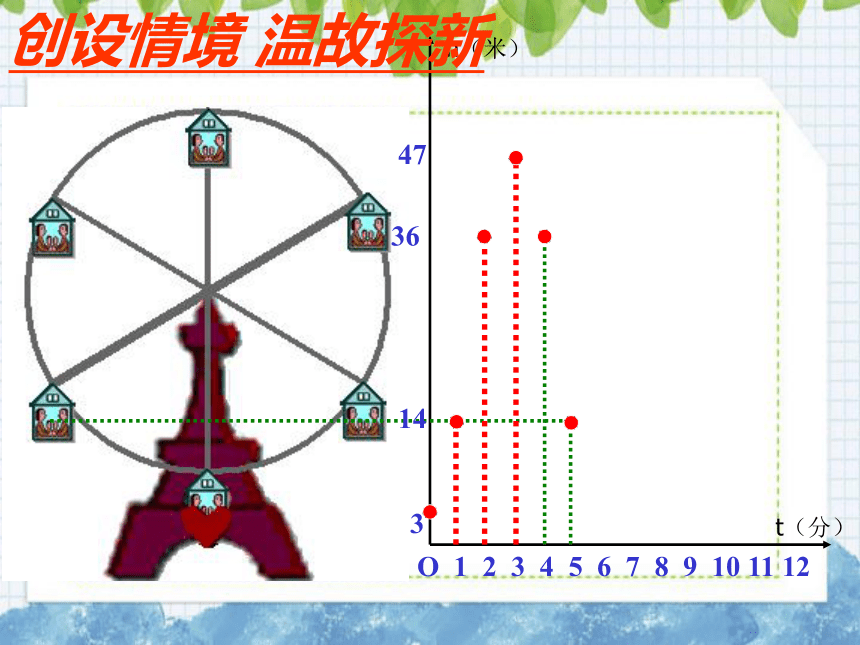
创设情境
温故探新
O
1
2
3
4
5
6
7
8
9
10
11
12
3
14
36
47
h(米)
t(分)
创设情境
温故探新
O
1
2
3
4
5
6
7
8
9
10
11
12
3
14
36
47
h(米)
t(分)
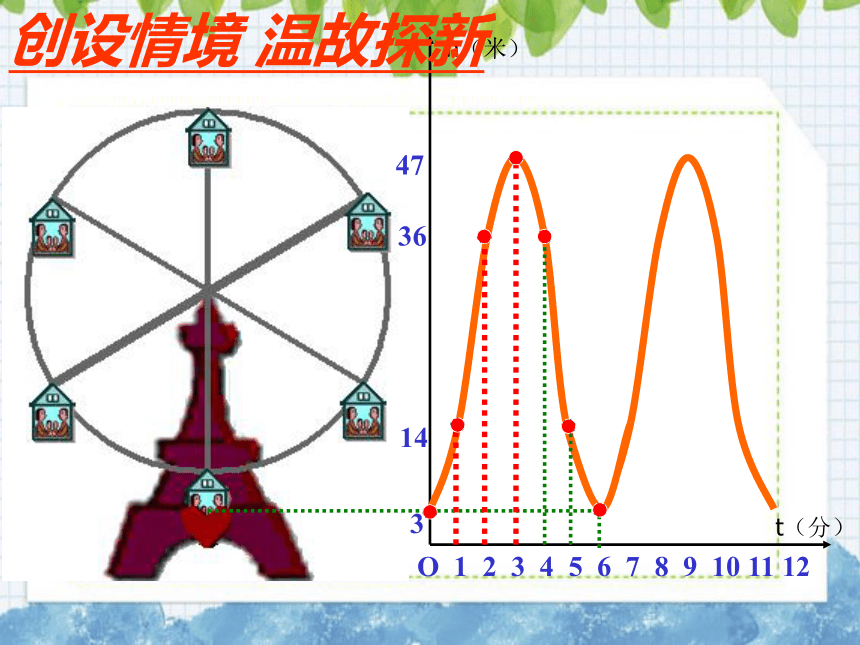
创设情境
温故探新
O
1
2
3
4
5
6
7
8
9
10
11
12
3
14
36
47
h(米)
t(分)
创设情境
温故探新
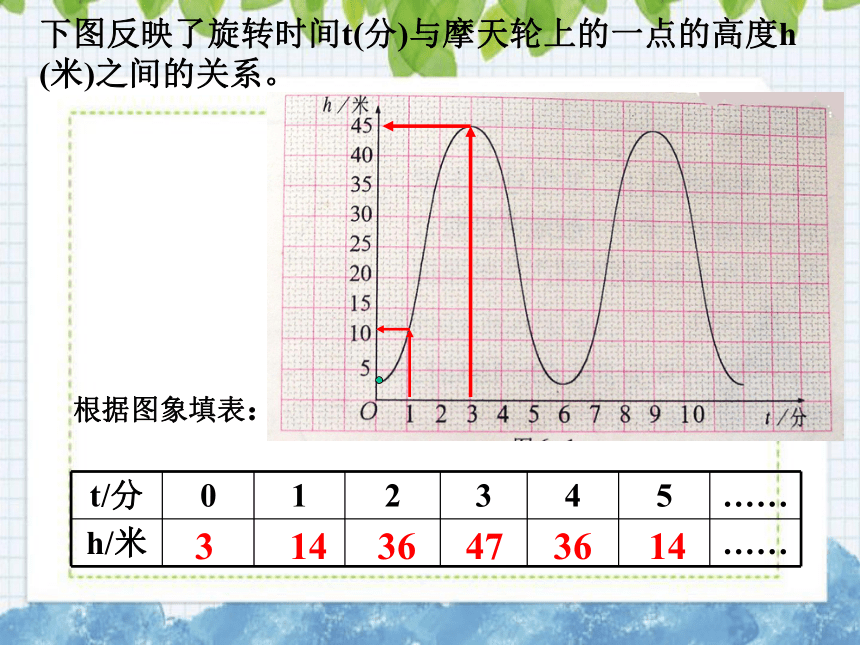
根据图象填表:
t/分
0
1
2
3
4
5
……
h/米
……
14
36
47
36
3
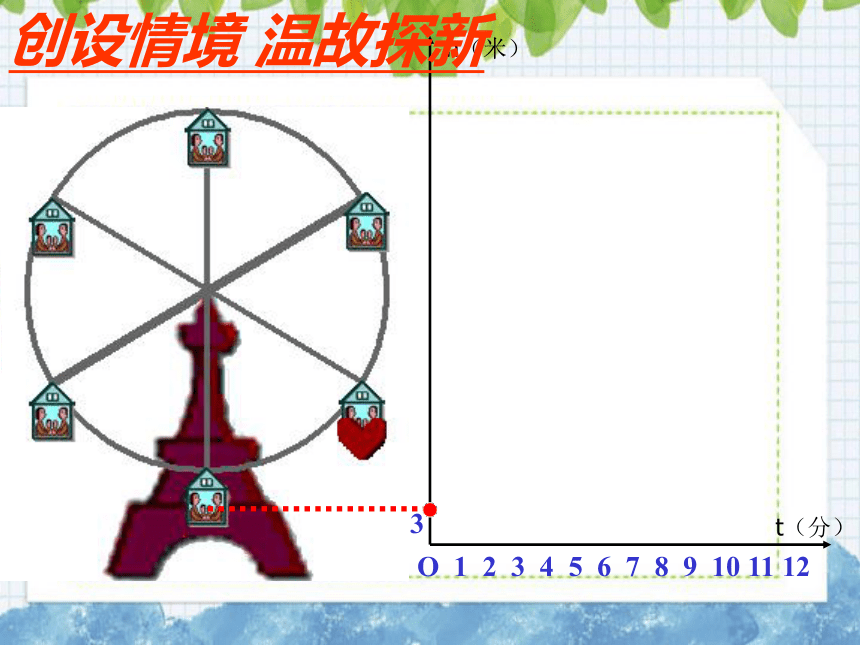
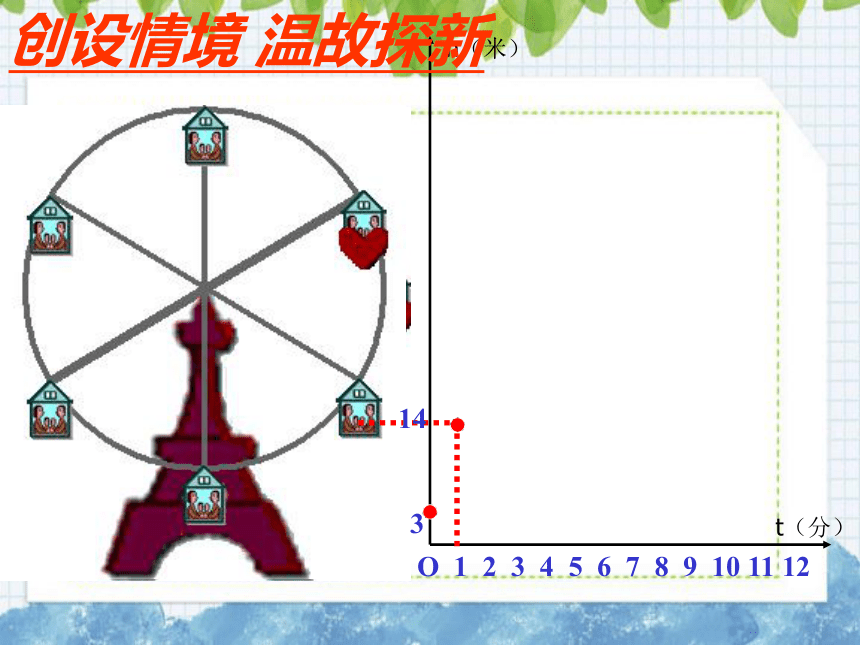
下图反映了旋转时间t(分)与摩天轮上的一点的高度h
(米)之间的关系。
14
对于给定的时间
t
,相应的高度
h
确定吗?
本题中反应了哪两个变量之间的关系?
旋转时间t(分)与摩天轮上的一点的高度h
对于给定的时间
t
,相应的高度
h随之确定。
创设情境
温故探新
瓶子或罐头盒等圆柱形的物体,常常如图摆放。
1、随着层数的增加,物体的总数将如何变化?
2、请填写下表:
层数n
1
2
3
4
5
……
物体总数y
……
3
6
10
15
1
合作交流探究新知
对于给定的层数
n
,相应的物体总数
y
确定吗?
想一想
本题中反应了哪两个变量之间的关系?
层数
n与物体总数
y
对于给定的层数
n
,相应的物体总数
y随之确定。
合作交流探究新知
问题3:一定质量的气体在体积不变时,假若温度降低到-273℃,则气体的压强为零.因此,物理学把-273℃作为热力学温度的零度.热力学温度T(K)与摄氏温度t(℃)之间有如下数量关系:T=t+273,T≥0.
(1)当t分别等于-43
℃
,-27
℃
,0
℃
,18
℃时,相应的热力学温度T是多少?
(2)给定一个大于-273
℃的t值,你能求出相应的T值吗?
230k,
246k,
273k,
291k
合作交流探究新知
本题中反应了哪两个变量之间的关系?
摄氏温度t(
℃)与热力学温度T(K)。
对于给定的一个t值,你能求出相应的T值吗?这个T值确定吗?唯一吗?
合作交流探究新知
上面的三个问题中,有什么共同特点?
①时间
t
、高度
h
;
②层数n、物体总数y;
③摄氏温度t、热力学温度T。
都有两个变量。
注意:给定其中某一个变量的值,相应地就确定了另一个变量的值。
合作交流探究新知
在某一变化过程中,有两个变量x、和y,并且对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们就称y是x的函数,其中x是自变量,y
是因变量。
一个x值
一个y值
y就是x的函数
对应
函数的概念:
即:
合作交流探究新知
回顾摩天轮,h是t的函数吗
引伸:t是h的函数吗?
每个时间t都只有一个h
和它对应,h就是t的
函数
当高度h为30时,
对应的时间t多个。
所以t不是h的函数
判断甲变量是否是乙变量的函数,就看乙变量取一个值时,
甲变量是否只有唯一值和它对应。
合作交流探究新知
1、y与x
的图象如图所示,问y是x的函数吗?
x
y
o
1
2
-2
判断甲变量是否是乙变量的函数,就看乙变量取一个值时,
甲变量是否只有唯一值和它对应。
合作交流探究新知
那么,以上三个问题,都用到了什么方法来表示函数呢?
合作交流探究新知
根据图象填表:
t/分
0
1
2
3
4
5
……
h/米
……
11
11
37
45
37
3
问题一:下图反映了旋转时间t(分)与摩天轮上的一点的高度h
(米)之间的关系。
图象法、
列表法
函数的表示法:
合作交流探究新知
问题二:罐头盒等圆柱形的物体常常如下图那样堆放。随着层数的增加,物体的总数是如何变化的?
填写下表:
层数n
1
2
3
4
5
……
物体总数y
……
6
10
15
1
3
合作交流探究新知
问题三:一定质量的气体在体积不变时,假若温度降低到-273℃,则气体的压强为零.因此,物理学把-273℃作为热力学温度的零度.热力学温度T(K)与摄氏温度t(℃)之间有如下数量关系:T=t+273,T≥0.
函数的表示法:
关系式法(解析式法)
合作交流探究新知
函数的表示法
(1)图象法
(2)列表法
(3)关系式法
思考:
对于问题二,你能用关系式法来表示吗?
三种表达形式都
可以相互转化
合作交流探究新知
1、上述的三个问题中,自变量能取哪些值?
合作交流探究新知
下图反映了摩天轮上的一点的高度h
(m)与旋转时间t(min)
之间的关系。
t/分
0
1
2
3
4
5
……
h/米
……
11
37
45
37
3
10
(1)根据上图填表:
t≥0
自变量t的取值范围
。
问题二:罐头盒等圆柱形的物体常常如下图那样堆放。
随着层数的增加,物体的总数是如何变化的?
填写下表:
层数n
1
2
3
4
5
……
物体总数y
……
6
10
15
1
3
自变量n的取值范围
。
n取正整数
问题三:一定质量的气体在体积不变时,假若温度降低到-273℃,则气体的压强为零.因此,物理学把-273℃作为热力学温度的零度.热力学温度T(K)与摄氏温度t(℃)之间有如下数量关系:T=t+273,T≥0.
自变量t的取值范围
。
t≥-273℃
1、上述的三个问题中,自变量能取哪些值?
注意:对于实际问题中,自变量的取值应使实际问题有意义。
2、什么叫函数值?如何求函数值?
合作交流探究新知
下图反映了摩天轮上的一点的高度h
(m)与旋转时间t(min)
之间的关系。
t/分
0
1
2
3
4
5
……
h/米
……
11
37
45
37
3
10
(1)根据上图填表:
问题二:罐头盒等圆柱形的物体常常如下图那样堆放。
随着层数的增加,物体的总数是如何变化的?
填写下表:
层数n
1
2
3
4
5
……
物体总数y
……
6
10
15
1
3
自变量n的取值范围
。
n取正整数
问题三:一定质量的气体在体积不变时,假若温度降低到-273℃,则气体的压强为零.因此,物理学把-273℃作为热力学温度的零度.热力学温度T(K)与摄氏温度t(℃)之间有如下数量关系:T=t+273,T≥0.
(1)当t分别等于-43,-27,0,18时,相应的热力学温度T是多少?
230,246,
273,291
(2)给定一个大于-273
℃的t值,你能求出相应的T值吗?
2、什么叫函数值?如何求函数值?
对于自变量在可取值范围内的一个确定的值a,函数有唯一确定的对应值,这个对应值称为当自变量等于a时的函数值。
合作交流探究新知
2.课本第77页
反馈练习巩固新知
1、指出下列变化关系中,哪些y是x的函数?那些不是?
①xy=2;②x2+y2=10;③x+y=5;④∣y∣=3x+1;⑤y=x2-4x+5
1、函数的概念:
2、函数的表示方法:
3、函数的自变量的取值范围:
4、函数值的求法:
(1)图象法
(2)列表法
(3)关系式法
课堂小结布置作业
习题6.1:
第1题
第2题
课堂小结布置作业
人生的价值,并不是用时间,而是用深度去衡量的。
——列夫·托尔斯泰
我们生活在一个变化的世界中,在我们的周围充满着许许多多变化的量。
你能从生活中举出
一些发生变化的
量吗?
你了解这些变量之间的关系吗?
创设情境
温故探新
问题一:你坐过摩天轮吗?想一想,如果你坐在摩天轮上时,随着时间的变化,你离开地面的高度是如何变化的?
创设情境
温故探新
O
1
2
3
4
5
6
7
8
9
10
11
12
h(米)
t(分)
创设情境
温故探新
O
1
2
3
4
5
6
7
8
9
10
11
12
3
h(米)
t(分)
创设情境
温故探新
O
1
2
3
4
5
6
7
8
9
10
11
12
3
14
h(米)
t(分)
创设情境
温故探新
O
1
2
3
4
5
6
7
8
9
10
11
12
3
14
36
h(米)
t(分)
创设情境
温故探新
O
1
2
3
4
5
6
7
8
9
10
11
12
3
14
37
47
h(米)
t(分)
创设情境
温故探新
O
1
2
3
4
5
6
7
8
9
10
11
12
3
14
36
47
h(米)
t(分)
创设情境
温故探新
O
1
2
3
4
5
6
7
8
9
10
11
12
3
14
36
47
h(米)
t(分)
创设情境
温故探新
O
1
2
3
4
5
6
7
8
9
10
11
12
3
14
36
47
h(米)
t(分)
创设情境
温故探新
根据图象填表:
t/分
0
1
2
3
4
5
……
h/米
……
14
36
47
36
3
下图反映了旋转时间t(分)与摩天轮上的一点的高度h
(米)之间的关系。
14
对于给定的时间
t
,相应的高度
h
确定吗?
本题中反应了哪两个变量之间的关系?
旋转时间t(分)与摩天轮上的一点的高度h
对于给定的时间
t
,相应的高度
h随之确定。
创设情境
温故探新
瓶子或罐头盒等圆柱形的物体,常常如图摆放。
1、随着层数的增加,物体的总数将如何变化?
2、请填写下表:
层数n
1
2
3
4
5
……
物体总数y
……
3
6
10
15
1
合作交流探究新知
对于给定的层数
n
,相应的物体总数
y
确定吗?
想一想
本题中反应了哪两个变量之间的关系?
层数
n与物体总数
y
对于给定的层数
n
,相应的物体总数
y随之确定。
合作交流探究新知
问题3:一定质量的气体在体积不变时,假若温度降低到-273℃,则气体的压强为零.因此,物理学把-273℃作为热力学温度的零度.热力学温度T(K)与摄氏温度t(℃)之间有如下数量关系:T=t+273,T≥0.
(1)当t分别等于-43
℃
,-27
℃
,0
℃
,18
℃时,相应的热力学温度T是多少?
(2)给定一个大于-273
℃的t值,你能求出相应的T值吗?
230k,
246k,
273k,
291k
合作交流探究新知
本题中反应了哪两个变量之间的关系?
摄氏温度t(
℃)与热力学温度T(K)。
对于给定的一个t值,你能求出相应的T值吗?这个T值确定吗?唯一吗?
合作交流探究新知
上面的三个问题中,有什么共同特点?
①时间
t
、高度
h
;
②层数n、物体总数y;
③摄氏温度t、热力学温度T。
都有两个变量。
注意:给定其中某一个变量的值,相应地就确定了另一个变量的值。
合作交流探究新知
在某一变化过程中,有两个变量x、和y,并且对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们就称y是x的函数,其中x是自变量,y
是因变量。
一个x值
一个y值
y就是x的函数
对应
函数的概念:
即:
合作交流探究新知
回顾摩天轮,h是t的函数吗
引伸:t是h的函数吗?
每个时间t都只有一个h
和它对应,h就是t的
函数
当高度h为30时,
对应的时间t多个。
所以t不是h的函数
判断甲变量是否是乙变量的函数,就看乙变量取一个值时,
甲变量是否只有唯一值和它对应。
合作交流探究新知
1、y与x
的图象如图所示,问y是x的函数吗?
x
y
o
1
2
-2
判断甲变量是否是乙变量的函数,就看乙变量取一个值时,
甲变量是否只有唯一值和它对应。
合作交流探究新知
那么,以上三个问题,都用到了什么方法来表示函数呢?
合作交流探究新知
根据图象填表:
t/分
0
1
2
3
4
5
……
h/米
……
11
11
37
45
37
3
问题一:下图反映了旋转时间t(分)与摩天轮上的一点的高度h
(米)之间的关系。
图象法、
列表法
函数的表示法:
合作交流探究新知
问题二:罐头盒等圆柱形的物体常常如下图那样堆放。随着层数的增加,物体的总数是如何变化的?
填写下表:
层数n
1
2
3
4
5
……
物体总数y
……
6
10
15
1
3
合作交流探究新知
问题三:一定质量的气体在体积不变时,假若温度降低到-273℃,则气体的压强为零.因此,物理学把-273℃作为热力学温度的零度.热力学温度T(K)与摄氏温度t(℃)之间有如下数量关系:T=t+273,T≥0.
函数的表示法:
关系式法(解析式法)
合作交流探究新知
函数的表示法
(1)图象法
(2)列表法
(3)关系式法
思考:
对于问题二,你能用关系式法来表示吗?
三种表达形式都
可以相互转化
合作交流探究新知
1、上述的三个问题中,自变量能取哪些值?
合作交流探究新知
下图反映了摩天轮上的一点的高度h
(m)与旋转时间t(min)
之间的关系。
t/分
0
1
2
3
4
5
……
h/米
……
11
37
45
37
3
10
(1)根据上图填表:
t≥0
自变量t的取值范围
。
问题二:罐头盒等圆柱形的物体常常如下图那样堆放。
随着层数的增加,物体的总数是如何变化的?
填写下表:
层数n
1
2
3
4
5
……
物体总数y
……
6
10
15
1
3
自变量n的取值范围
。
n取正整数
问题三:一定质量的气体在体积不变时,假若温度降低到-273℃,则气体的压强为零.因此,物理学把-273℃作为热力学温度的零度.热力学温度T(K)与摄氏温度t(℃)之间有如下数量关系:T=t+273,T≥0.
自变量t的取值范围
。
t≥-273℃
1、上述的三个问题中,自变量能取哪些值?
注意:对于实际问题中,自变量的取值应使实际问题有意义。
2、什么叫函数值?如何求函数值?
合作交流探究新知
下图反映了摩天轮上的一点的高度h
(m)与旋转时间t(min)
之间的关系。
t/分
0
1
2
3
4
5
……
h/米
……
11
37
45
37
3
10
(1)根据上图填表:
问题二:罐头盒等圆柱形的物体常常如下图那样堆放。
随着层数的增加,物体的总数是如何变化的?
填写下表:
层数n
1
2
3
4
5
……
物体总数y
……
6
10
15
1
3
自变量n的取值范围
。
n取正整数
问题三:一定质量的气体在体积不变时,假若温度降低到-273℃,则气体的压强为零.因此,物理学把-273℃作为热力学温度的零度.热力学温度T(K)与摄氏温度t(℃)之间有如下数量关系:T=t+273,T≥0.
(1)当t分别等于-43,-27,0,18时,相应的热力学温度T是多少?
230,246,
273,291
(2)给定一个大于-273
℃的t值,你能求出相应的T值吗?
2、什么叫函数值?如何求函数值?
对于自变量在可取值范围内的一个确定的值a,函数有唯一确定的对应值,这个对应值称为当自变量等于a时的函数值。
合作交流探究新知
2.课本第77页
反馈练习巩固新知
1、指出下列变化关系中,哪些y是x的函数?那些不是?
①xy=2;②x2+y2=10;③x+y=5;④∣y∣=3x+1;⑤y=x2-4x+5
1、函数的概念:
2、函数的表示方法:
3、函数的自变量的取值范围:
4、函数值的求法:
(1)图象法
(2)列表法
(3)关系式法
课堂小结布置作业
习题6.1:
第1题
第2题
课堂小结布置作业
人生的价值,并不是用时间,而是用深度去衡量的。
——列夫·托尔斯泰
