鲁教版(五四制)七上 6.5《一次函数的应用》课件(31张PPT)
文档属性
| 名称 | 鲁教版(五四制)七上 6.5《一次函数的应用》课件(31张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-02 14:55:45 | ||
图片预览





文档简介
(共31张PPT)
《一次函数的应用》
01
02
03
04
问题情境
例题讲解
课堂小结
反馈练习
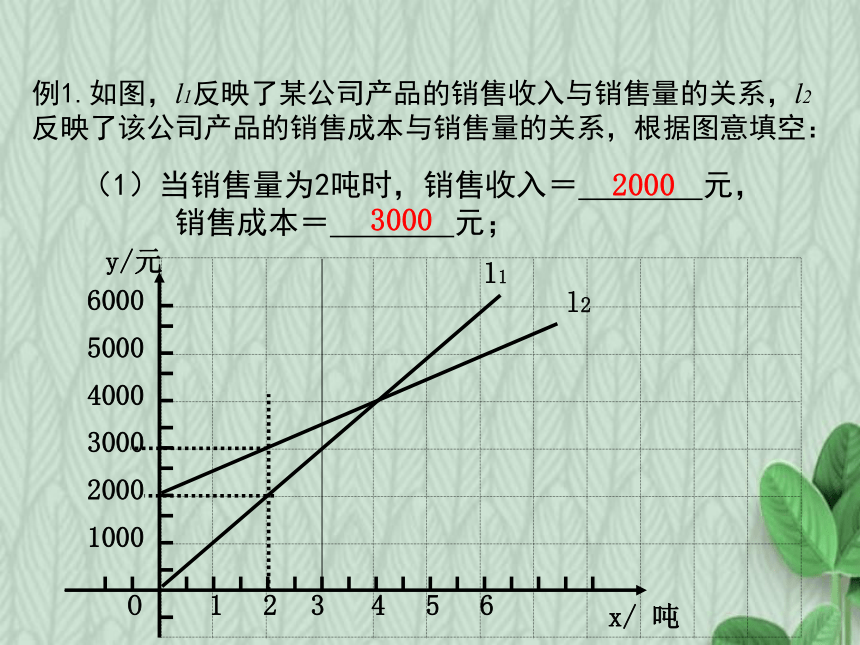
例1.如图,l1反映了某公司产品的销售收入与销售量的关系,l2反映了该公司产品的销售成本与销售量的关系,根据图意填空:
(1)当销售量为2吨时,销售收入= 元,
销售成本= 元;
2000
x/
吨
y/元
O
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
3000
l2
l1
⑵当销售量为6吨时,销售收入= 元,
销售成本= 元;
6000
5000
⑶当销售量为 时,销售收入等于销售成本;
4吨
x/
吨
y/元
O
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
l2
l1
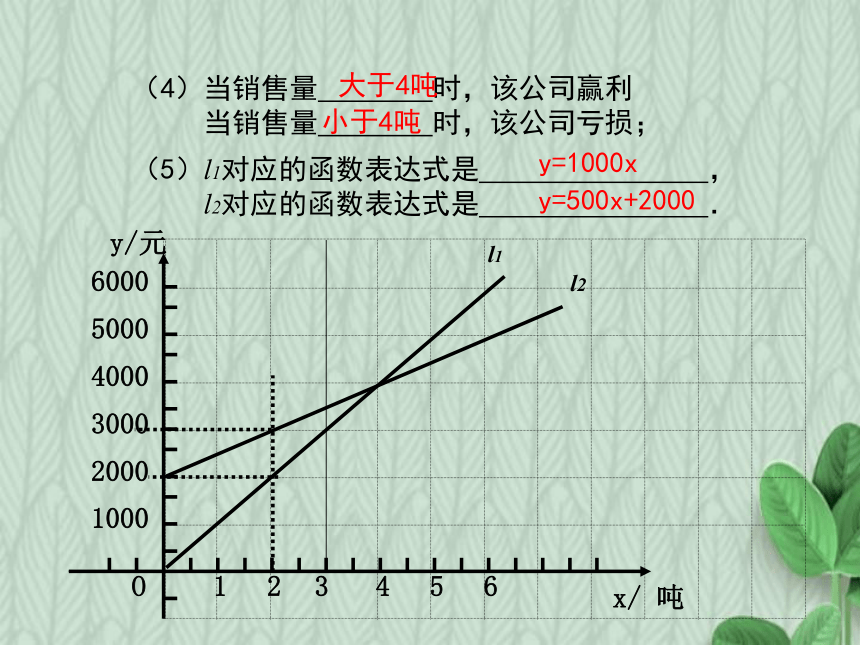
(4)当销售量 时,该公司赢利
当销售量 时,该公司亏损;
大于4吨
小于4吨
(5)l1对应的函数表达式是 ,
l2对应的函数表达式是 .
y=1000x
y=500x+2000
x/
吨
y/元
O
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
l2
l1
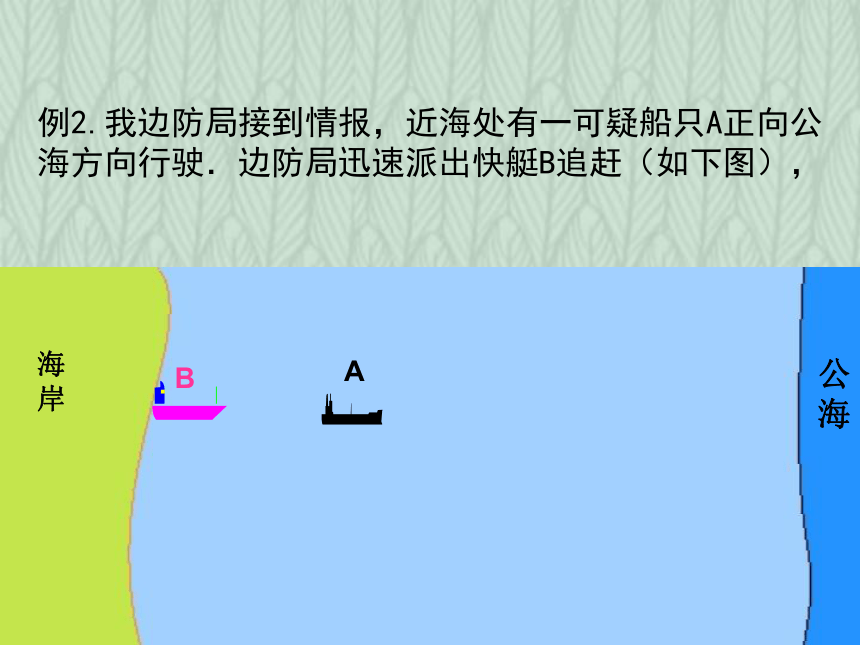
例2.我边防局接到情报,近海处有一可疑船只A正向公海方向行驶.边防局迅速派出快艇B追赶(如下图),
海
岸
公
海
A
B
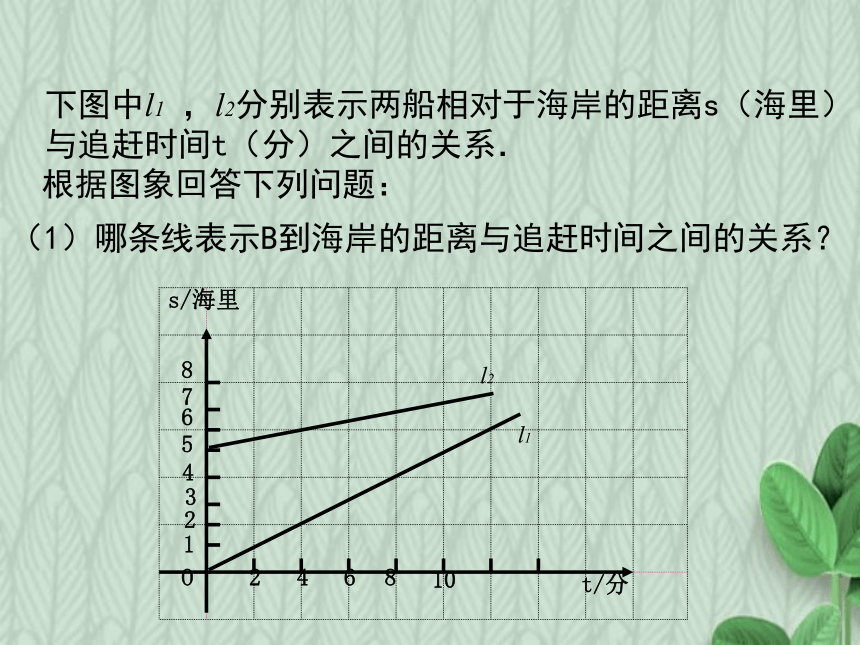
下图中l1
,l2分别表示两船相对于海岸的距离s(海里)与追赶时间t(分)之间的关系.
根据图象回答下列问题:
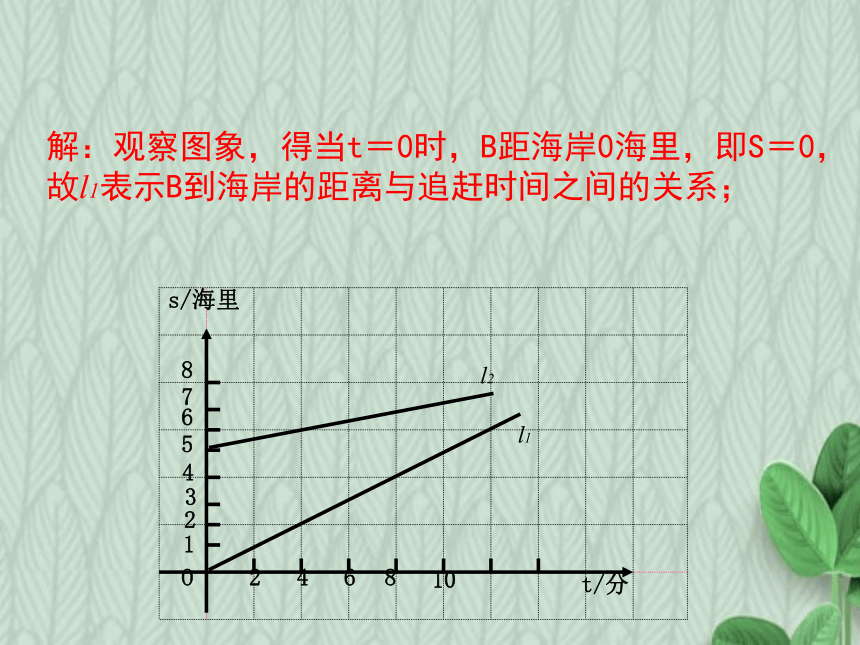
(1)哪条线表示B到海岸的距离与追赶时间之间的关系?
2
4
6
8
10
O
1
2
3
4
5
6
7
8
t/分
s/海里
l1
l2
解:观察图象,得当t=0时,B距海岸0海里,即S=0,故l1表示B到海岸的距离与追赶时间之间的关系;
2
4
6
8
10
O
1
2
3
4
5
6
7
8
t/分
s/海里
l1
l2
2
4
6
8
10
O
1
2
3
4
5
6
7
8
t/分
s/海里
l1
l2
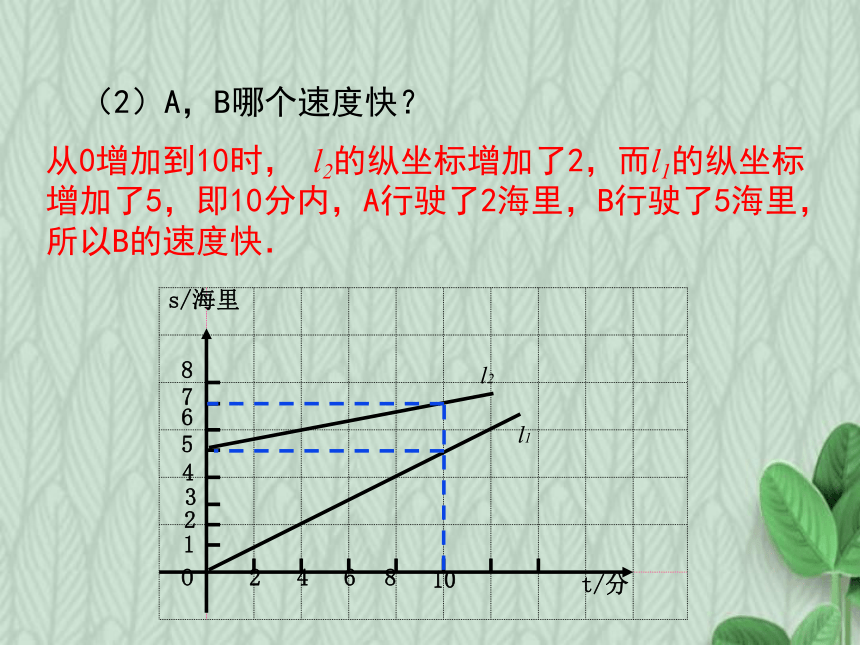
(2)A,B哪个速度快?
从0增加到10时,
l2的纵坐标增加了2,而l1的纵坐标增加了5,即10分内,A行驶了2海里,B行驶了5海里,所以B的速度快.
2
4
6
8
10
O
1
2
3
4
5
6
7
8
t/分
s/海里
l1
l2
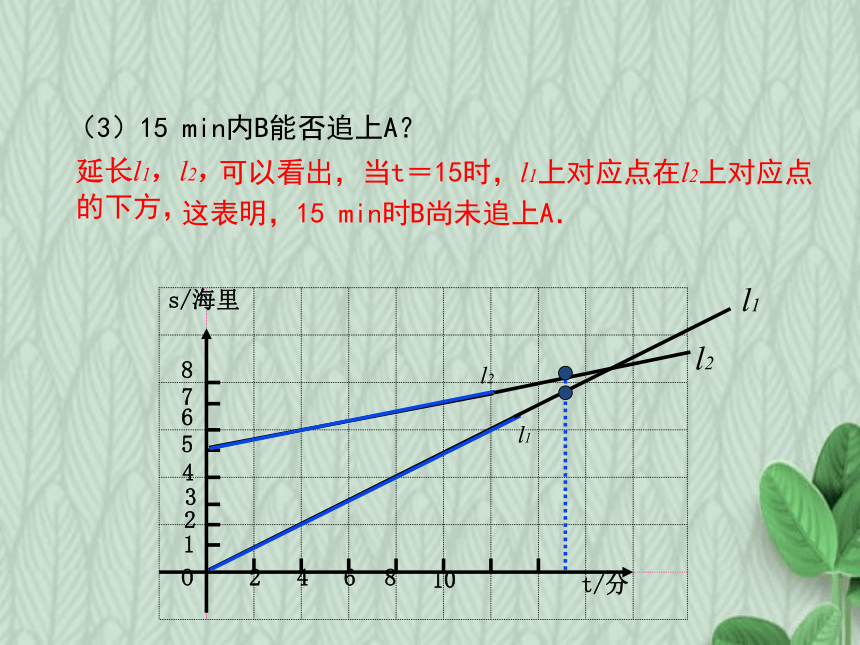
(3)15
min内B能否追上A?
l1
l2
延长l1,l2,
可以看出,当t=15时,l1上对应点在l2上对应点的下方,
这表明,15
min时B尚未追上A.
如图l1
,l2相交于点P.
(4)如果一直追下去,那么B能否追上A?
因此,如果一直追下去,那么B一定能追上A.
2
4
6
8
10
O
1
2
3
4
5
6
7
8
t/分
s/海里
l1
l2
l1
l2
P
(5)当A逃到离海岸12海里的公海时,B将无法对其进行检查.照此速度,B能否在A逃入公海前将其拦截?
2
4
6
8
10
O
1
2
3
4
5
6
7
8
t/分
s/海里
l1
l2
l1
l2
P
从图中可以看出,l1与l2交点P的纵坐标小于12
,
这说明在A逃入公海前,我边防快艇B能够追上A.
从图中可以看出,l1与l2交点P的纵坐标小于12,这说明在A逃入公海前,我边防快艇B能够追上A.
想一想你能用其他方法解决上述问题吗?
2
4
6
8
10
O
1
2
3
4
5
6
7
8
t/分
s/海里
l1
l2
l1
l2
P
一农民带上若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系,如图所示,结合图象回答下列问题.
(4)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,试问他一共带了多少千克土豆?
(1)农民自带的零钱是多少?
(2)试求降价前y与x之间的关系式.
(3)由表达式你能求出降价前每千克的土豆价格是多少?
例.
小聪和小慧去某风景区游览,约好在“飞瀑”见面,上午7:00小聪乘电动汽车从“古刹”出发,沿景区公路去“飞瀑”,车速为36km/h,小慧也于上午7:00从“塔林”出发,骑电动自行车沿景区公路去“飞瀑”,车速为26km/h.
10km
10km
25km
(1)当小聪追上小慧时,他们是否已经过了“草甸”?
(2)当小聪到达“飞瀑”时,小慧离“飞瀑”还有多少km?
分析:⑴两个人是否同时起步?
⑶这个问题中的两个变量是什么?它们涉及的是什么函数关系?
⑵在两个人到达之前所用时间是否相同?所行驶的路程是否相同?出发地点是否相同?两个人的速度各是多少?
⑷如果用S表示路程,t表示时间,那么他们的函数解析式是一样的吗?
他们各自的解析式分别是什么?
小聪的解析式为________________
小慧的解析式为________________
S1=36t
S2=26t+10
当小聪追上小慧时,说明他们两个人的什么量是相同的?
是否已经过了“草甸”该用什么量来表示?
你会选择用哪种方式来解决?图象法?还是解析法?
解:设经过t时,小聪与小慧离“古刹”的路程分别为S1、S2,
由题意得:S1=36t,
S2=26t+10
将这两个函数解析式画在同一个直角坐标系上,观察图象,得
36
5
10
20
30
40
50
60
15
25
35
45
55
0.25
0
0.5
0.75
1
1.25
1.5
1.75
S1=36t
S2=26t+10
t(时)
S(km)
⑴两条直线S1=36t,
S2=26t+10的交点坐标为
(1,36)
这说明当小聪追上小慧时,S1=S2=36
km,即离“古刹”36km,已超过35km,也就是说,他们已经过了“草甸”
36
5
10
20
30
40
50
60
15
25
35
45
55
0.25
0
0.5
0.75
1
1.25
1.5
1.75
S1=36t
S2=26t+10
t(时)
S(km)
42.5
⑵当小聪到达“飞瀑”时,即S1=45km,
此时S2=42.5km。
所以小慧离“飞瀑”还有45-42.5=2.5(km)
思考:用解析法如何求得这两个问题的结果?
5
10
20
30
40
50
60
15
25
35
45
55
0.25
0
0.5
0.75
1
1.25
1.5
1.75
S1=36t
S2=26t+10
t(时)
S(km)
观察甲、乙两图,解答下列问题
1.填空:两图中的
(____)图比较符合传统寓言故事《龟免赛跑》中所描述的情节.
2.
根据1中所填答案的图象填写下表:
绿
线
红
线
平均速度
(米/分)
最快速度
(米/分)
到达
时间(分)
主人公
(龟或免)
项目
线型
3.
根据1中所填答案的图象求:
(1)龟免赛跑过程中的函数关系式(要注明各函数的自变量的取值范围);
(2)乌龟经过多长时间追上了免子,追及地距起点有多远的路程?
4.
请你根据另一幅图表,充分发挥你的想象,自编一则新的“龟免赛跑”的寓言故事,要求如下:
(1)用简洁明快的语言概括大意,不能超过200字;
(2)图表中能确定的数值,在故事叙述中不得少于3个,且要分别涉及时间、路和速度这三个量.
5、如图,lA与
lB分别表示A步行与B骑车同一路上行驶的路程S与时间t的关系.
(1)B出发时与A相距多少千米?
(2)走了一段路后,自行车发生故障,进行修理,所用的时间是多少小时?
(3)B出发后经过多少小时与A相遇?
S(千米)
t(时)
O
10
22.5
7.5
0.5
3
1.5
lB
lA
(4)若B的自行车不发生故障,保持出发时的速度前进,那么经过多少时间与A相遇?相遇点离B的出发点多远?你能用哪些方法解决这个问题?在图中表示出这个相遇点C.
S(千米)
t(时)
O
10
22.5
7.5
0.5
3
1.5
lB
lA
6.甲、乙两班参加植树活动,乙班先植树30棵,然后甲班才开始与乙班一起植树.设甲班植树的总量为y甲(棵),乙班植树的总量为y乙(棵),两班一起植树所用的时间(从甲班开始植树时计时)为x(时),
y甲、
y乙与
x之间的部分函数图象如图所示.
O
y(棵)
x(时)
3
6
8
120
30
(1)当0≤x≤6时,分别求y甲、
y乙与x之间的函数关系式.
(2)如果甲、乙两班均保持前6个小时的工作效率,通过计算说明,当x=8时,甲、乙两班植树的总量之和能否超过260棵.
(3)如果6个小时后,甲班保持前6个小时的工作效率,乙班通过增加人数,提高了工作效率,这样继续植树2小时,活动结束.当x=8时,两班之间植树的总量相差20棵,求乙班增加人数后平均每小时植树多少棵.
在运用一次函数解决实际问题时,首先判断问题中的两个变量之间是不是一次函数关系,当确定是一次函数关系时,可求出函数解析式,并运用一次函数的图象和性质进一步求得我们所需要的结果.
复习、回顾
《一次函数的应用》
01
02
03
04
问题情境
例题讲解
课堂小结
反馈练习
例1.如图,l1反映了某公司产品的销售收入与销售量的关系,l2反映了该公司产品的销售成本与销售量的关系,根据图意填空:
(1)当销售量为2吨时,销售收入= 元,
销售成本= 元;
2000
x/
吨
y/元
O
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
3000
l2
l1
⑵当销售量为6吨时,销售收入= 元,
销售成本= 元;
6000
5000
⑶当销售量为 时,销售收入等于销售成本;
4吨
x/
吨
y/元
O
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
l2
l1
(4)当销售量 时,该公司赢利
当销售量 时,该公司亏损;
大于4吨
小于4吨
(5)l1对应的函数表达式是 ,
l2对应的函数表达式是 .
y=1000x
y=500x+2000
x/
吨
y/元
O
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
l2
l1
例2.我边防局接到情报,近海处有一可疑船只A正向公海方向行驶.边防局迅速派出快艇B追赶(如下图),
海
岸
公
海
A
B
下图中l1
,l2分别表示两船相对于海岸的距离s(海里)与追赶时间t(分)之间的关系.
根据图象回答下列问题:
(1)哪条线表示B到海岸的距离与追赶时间之间的关系?
2
4
6
8
10
O
1
2
3
4
5
6
7
8
t/分
s/海里
l1
l2
解:观察图象,得当t=0时,B距海岸0海里,即S=0,故l1表示B到海岸的距离与追赶时间之间的关系;
2
4
6
8
10
O
1
2
3
4
5
6
7
8
t/分
s/海里
l1
l2
2
4
6
8
10
O
1
2
3
4
5
6
7
8
t/分
s/海里
l1
l2
(2)A,B哪个速度快?
从0增加到10时,
l2的纵坐标增加了2,而l1的纵坐标增加了5,即10分内,A行驶了2海里,B行驶了5海里,所以B的速度快.
2
4
6
8
10
O
1
2
3
4
5
6
7
8
t/分
s/海里
l1
l2
(3)15
min内B能否追上A?
l1
l2
延长l1,l2,
可以看出,当t=15时,l1上对应点在l2上对应点的下方,
这表明,15
min时B尚未追上A.
如图l1
,l2相交于点P.
(4)如果一直追下去,那么B能否追上A?
因此,如果一直追下去,那么B一定能追上A.
2
4
6
8
10
O
1
2
3
4
5
6
7
8
t/分
s/海里
l1
l2
l1
l2
P
(5)当A逃到离海岸12海里的公海时,B将无法对其进行检查.照此速度,B能否在A逃入公海前将其拦截?
2
4
6
8
10
O
1
2
3
4
5
6
7
8
t/分
s/海里
l1
l2
l1
l2
P
从图中可以看出,l1与l2交点P的纵坐标小于12
,
这说明在A逃入公海前,我边防快艇B能够追上A.
从图中可以看出,l1与l2交点P的纵坐标小于12,这说明在A逃入公海前,我边防快艇B能够追上A.
想一想你能用其他方法解决上述问题吗?
2
4
6
8
10
O
1
2
3
4
5
6
7
8
t/分
s/海里
l1
l2
l1
l2
P
一农民带上若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系,如图所示,结合图象回答下列问题.
(4)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,试问他一共带了多少千克土豆?
(1)农民自带的零钱是多少?
(2)试求降价前y与x之间的关系式.
(3)由表达式你能求出降价前每千克的土豆价格是多少?
例.
小聪和小慧去某风景区游览,约好在“飞瀑”见面,上午7:00小聪乘电动汽车从“古刹”出发,沿景区公路去“飞瀑”,车速为36km/h,小慧也于上午7:00从“塔林”出发,骑电动自行车沿景区公路去“飞瀑”,车速为26km/h.
10km
10km
25km
(1)当小聪追上小慧时,他们是否已经过了“草甸”?
(2)当小聪到达“飞瀑”时,小慧离“飞瀑”还有多少km?
分析:⑴两个人是否同时起步?
⑶这个问题中的两个变量是什么?它们涉及的是什么函数关系?
⑵在两个人到达之前所用时间是否相同?所行驶的路程是否相同?出发地点是否相同?两个人的速度各是多少?
⑷如果用S表示路程,t表示时间,那么他们的函数解析式是一样的吗?
他们各自的解析式分别是什么?
小聪的解析式为________________
小慧的解析式为________________
S1=36t
S2=26t+10
当小聪追上小慧时,说明他们两个人的什么量是相同的?
是否已经过了“草甸”该用什么量来表示?
你会选择用哪种方式来解决?图象法?还是解析法?
解:设经过t时,小聪与小慧离“古刹”的路程分别为S1、S2,
由题意得:S1=36t,
S2=26t+10
将这两个函数解析式画在同一个直角坐标系上,观察图象,得
36
5
10
20
30
40
50
60
15
25
35
45
55
0.25
0
0.5
0.75
1
1.25
1.5
1.75
S1=36t
S2=26t+10
t(时)
S(km)
⑴两条直线S1=36t,
S2=26t+10的交点坐标为
(1,36)
这说明当小聪追上小慧时,S1=S2=36
km,即离“古刹”36km,已超过35km,也就是说,他们已经过了“草甸”
36
5
10
20
30
40
50
60
15
25
35
45
55
0.25
0
0.5
0.75
1
1.25
1.5
1.75
S1=36t
S2=26t+10
t(时)
S(km)
42.5
⑵当小聪到达“飞瀑”时,即S1=45km,
此时S2=42.5km。
所以小慧离“飞瀑”还有45-42.5=2.5(km)
思考:用解析法如何求得这两个问题的结果?
5
10
20
30
40
50
60
15
25
35
45
55
0.25
0
0.5
0.75
1
1.25
1.5
1.75
S1=36t
S2=26t+10
t(时)
S(km)
观察甲、乙两图,解答下列问题
1.填空:两图中的
(____)图比较符合传统寓言故事《龟免赛跑》中所描述的情节.
2.
根据1中所填答案的图象填写下表:
绿
线
红
线
平均速度
(米/分)
最快速度
(米/分)
到达
时间(分)
主人公
(龟或免)
项目
线型
3.
根据1中所填答案的图象求:
(1)龟免赛跑过程中的函数关系式(要注明各函数的自变量的取值范围);
(2)乌龟经过多长时间追上了免子,追及地距起点有多远的路程?
4.
请你根据另一幅图表,充分发挥你的想象,自编一则新的“龟免赛跑”的寓言故事,要求如下:
(1)用简洁明快的语言概括大意,不能超过200字;
(2)图表中能确定的数值,在故事叙述中不得少于3个,且要分别涉及时间、路和速度这三个量.
5、如图,lA与
lB分别表示A步行与B骑车同一路上行驶的路程S与时间t的关系.
(1)B出发时与A相距多少千米?
(2)走了一段路后,自行车发生故障,进行修理,所用的时间是多少小时?
(3)B出发后经过多少小时与A相遇?
S(千米)
t(时)
O
10
22.5
7.5
0.5
3
1.5
lB
lA
(4)若B的自行车不发生故障,保持出发时的速度前进,那么经过多少时间与A相遇?相遇点离B的出发点多远?你能用哪些方法解决这个问题?在图中表示出这个相遇点C.
S(千米)
t(时)
O
10
22.5
7.5
0.5
3
1.5
lB
lA
6.甲、乙两班参加植树活动,乙班先植树30棵,然后甲班才开始与乙班一起植树.设甲班植树的总量为y甲(棵),乙班植树的总量为y乙(棵),两班一起植树所用的时间(从甲班开始植树时计时)为x(时),
y甲、
y乙与
x之间的部分函数图象如图所示.
O
y(棵)
x(时)
3
6
8
120
30
(1)当0≤x≤6时,分别求y甲、
y乙与x之间的函数关系式.
(2)如果甲、乙两班均保持前6个小时的工作效率,通过计算说明,当x=8时,甲、乙两班植树的总量之和能否超过260棵.
(3)如果6个小时后,甲班保持前6个小时的工作效率,乙班通过增加人数,提高了工作效率,这样继续植树2小时,活动结束.当x=8时,两班之间植树的总量相差20棵,求乙班增加人数后平均每小时植树多少棵.
在运用一次函数解决实际问题时,首先判断问题中的两个变量之间是不是一次函数关系,当确定是一次函数关系时,可求出函数解析式,并运用一次函数的图象和性质进一步求得我们所需要的结果.
复习、回顾
