鲁科版(2019)高中物理 必修第一册 2.2 位移变化规律 课件(共52张PPT)
文档属性
| 名称 | 鲁科版(2019)高中物理 必修第一册 2.2 位移变化规律 课件(共52张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-09-02 17:49:59 | ||
图片预览










文档简介
(共52张PPT)
位移变化规律
一、匀变速直线运动位移—时间关系
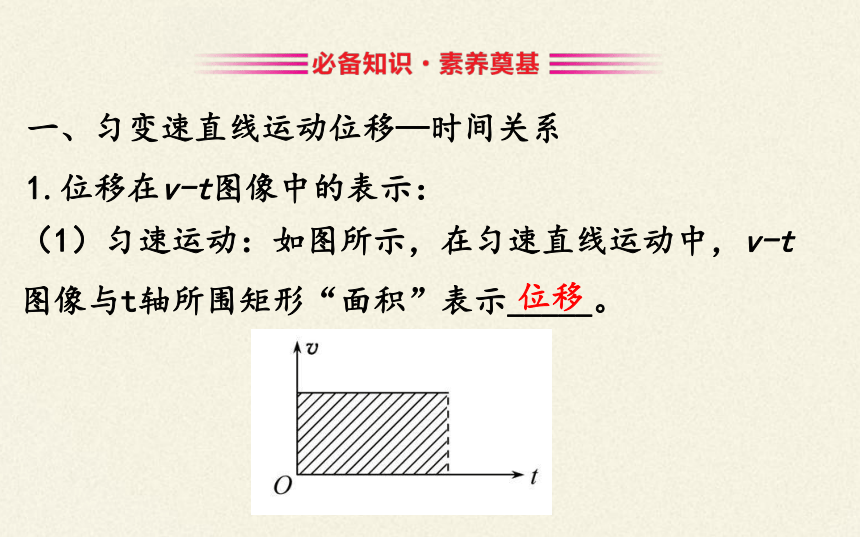
1.位移在v-t图像中的表示:
(1)匀速运动:如图所示,在匀速直线运动中,v-t图像与t轴所围矩形“面积”表示_____。
位移
(2)匀变速直线运动:
①微元法推导。
a.把物体的运动分成几个小段,如图甲,每段位移≈
每段起始时刻速度×每段的时间=对应矩形面积。所
以,整个过程的位移≈各个小矩形面积_____。
之和
b.把运动过程分为更多的小段,如图乙,各小矩形的
_________可以更精确地表示物体在整个过程的位移。
面积之和
c.把整个过程分得非常非常细,如图丙,小矩形合在
一起成了一个梯形,___________就代表物体在相应时
间间隔内的位移。
梯形的面积
②结论:做匀变速直线运动的物体的位移对应着v-t图
像中的___________________所包围的梯形面积。
图线与对应的时间轴
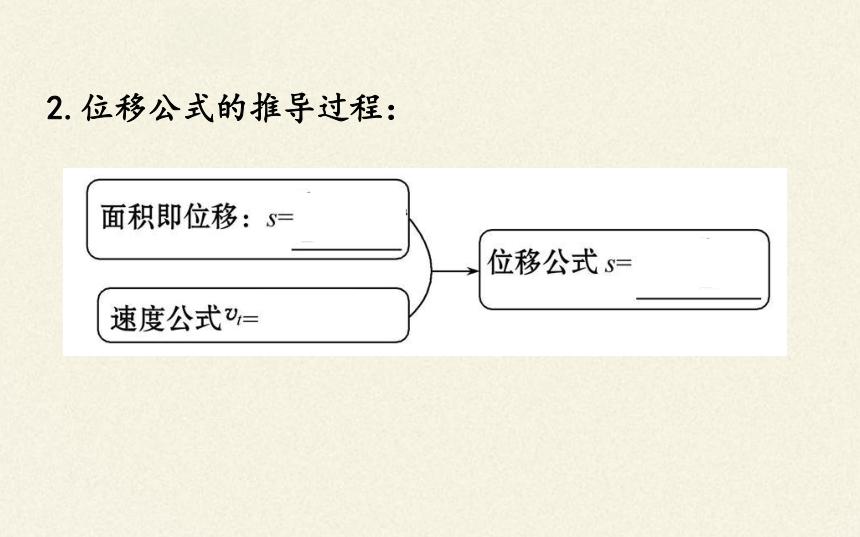
2.位移公式的推导过程:
3.位移—时间图像(s-t图像):
(1)画法:以横轴表示_____、纵轴表示_____,根据实
际数据选单位、定标度、描点,用平滑曲线连接各点
便得到s-t图像。
时间
位移
(2)图像性质:对于匀变速直线运动来说,位移是时间
的_________,其图像是一条二次函数的部分曲线,如
图。
二次函数
二、匀变速直线运动的位移—速度关系
一、公式s=v0t+
at2的应用
1.各物理量的意义:公式中s表示时间t内物体运动的位移,单位是m;v0表示初速度,单位是m/s;a表示加速度,单位是m/s2;t表示运动时间,单位是s。
2.适用条件:公式反映了位移随时间的变化规律,公式仅适用于匀变速直线运动位移的求解。
3.符号规定:公式中s、v0、a都是矢量,应用时必须选取统一的正方向,一般选取初速度v0的方向为正方向。
(1)若a与v0同向,a取正值,物体做匀加速直线运动。
(2)若a与v0反向,a取负值,物体做匀减速直线运动。
(3)若位移的计算结果为正值,说明这段时间内位移的
方向与规定的正方向相同。
(4)若位移的计算结果为负值,说明这段时间内位移的
方向与规定的正方向相反。
4.若v0=0,则s=
at2,位移与时间的二次方成正比。
【思考·讨论】
利用公式s=v0t+
at2求出的位移大小等于物体运动的
路程吗?(科学思维)
提示:不一定,当物体匀减速运动到速度为零再反向
以等大的加速度匀加速运动时,位移的大小小于路程。
【典例示范】
(2019·福州高一检测)一辆卡车初速度为v0=10m/s,以a=2m/s2的加速度行驶,求:
(1)卡车在3s末的速度大小v3。
(2)卡车在6s内的位移大小s6。
(3)卡车在第6s内的位移大小sⅥ。
【解题探究】
(1)3s末是时刻还是时间?
提示:3s末是一个瞬时,是时刻。
(2)“第6s内”是多长时间?“第6s内”的位移是6s内的总位移吗?
提示:“第6s内”是指1s的时间,其位移为第六个1s内的位移,不是6s内的总位移。
【解析】(1)卡车在3s末的速度为v3=v0+at3=(10+2×
3)m/s=16m/s。
(2)卡车在6s内的位移为s6=v0t6+
=(10×6+
×
2×36)m=96m。
(3)卡车在第6s内的位移为sⅥ=s6-s5=s6-(v0t5+
)
=96m-(10×5+
×2×25)m=21m。
答案:(1)16m/s (2)96m (3)21m
【误区警示】应用位移公式的两点注意
(1)公式s=v0t+
at2仅适用于匀变速直线运动。
(2)应用位移公式解题时常选初速度的方向为正方向,
物体若加速则加速度为正值,减速则加速度为负值。
【素养训练】
1.(多选)(2019·厦门高一检测)物体从静止开始做匀加速直线运动,第3s内通过的位移是3m,则( )
A.前3s的位移是6m
B.3s末的速度是3.6m/s
C.3s内的平均速度是2m/s
D.第5s内的平均速度是5.4m/s
【解析】选B、D。由位移公式s=
at2知,第3s内的
位移为
a×32m-a×
22m=3m,故加速度a=1.2m/s2,
所以前3s的位移s=
×1.2×32m=5.4m,A错误;
第3s末的速度v=at=1.2×3m/s=3.6m/s,B正确;
3s内的平均速度
=1.8m/s,C错误;
第5s内的平均速度等于第4.5s末的瞬时速度,
故v′=at′=1.2×4.5m/s=5.4m/s,D正确。
2.从静止开始做匀加速直线运动的汽车,经过t=10s,走过位移s=30m。求:
(1)汽车运动的加速度大小。
(2)汽车10s末的速度。
【解析】(1)根据匀变速直线运动位移公式得,
s=
at2,代入数据解得a=
=0.6m/s2。
(2)根据匀变速直线运动速度公式得汽车10s末的速
度v=at=6m/s。
答案:(1)0.6m/s2 (2)6m/s
【补偿训练】
1.以10m/s的速度行驶的列车,在下坡路上的加速度为0.2m/s2,经过30s到达坡底。求:
(1)到达坡底的速度。
(2)坡路的长度。
【解析】(1)根据速度公式,得列车到达坡底的速度为
vt=v0+at=10m/s+0.2×30m/s=16m/s
(2)根据位移公式得坡路的长度为
s=v0t+
at2=10×30m+
×0.2×302m=390m
答案:(1)16m/s (2)390m
2.一辆汽车在平直公路上做匀变速直线运动,公路边每隔15m有一棵树,如图所示,汽车通过A、B两相邻的树用了3s,通过B、C两相邻的树用了2s,求汽车运动的加速度大小和通过树B时的速度大小。
【解析】设汽车经过树A时速度为vA,加速度为a。对AB段运动,由s=v0t+
at2有:15m=vA×3s+a×
(3s)2
同理,对AC段运动,有:30m=vA×5s+a×
(5s)2
两式联立解得:vA=3.5m/s,a=1m/s2
再由速度公式vt=v0+at得:vB=3.5m/s+1m/s2×3s=6.5m/s
答案:1m/s2 6.5m/s
二、用v-t图像求位移
1.匀速直线运动的位移:
(1)做匀速直线运动的物体在时间t内的位移s=vt。
(2)做匀速直线运动的物体,其v-t图像是一条平行于时间轴的直线,其位移在数值上等于v-t图线与对应的时间轴所包围的矩形的面积。如图所示。
2.匀变速直线运动的位移:
(1)如图所示,图线与时间轴所围的梯形的面积就代表
物体在时间t内的位移,梯形的上底为v0,下底为v,
对应的时间为t,则有:s=(v0+v)t。
(2)因为t时刻的速度v=v0+at,所以位移与时间的关系
为s=
(v0+v0+at)t=v0t+
at2。
【典例示范】
(多选)(2019·龙岩高一检测)某物体运动的v-t图像如图所示,根据图像可知,该物体( )
A.在0到2s末的时间内,加速度为1m/s2
B.在0到5s末的时间内,位移为10m
C.在0到6s末的时间内,位移为7.5m
D.在0到6s末的时间内,位移为6.5m
【解题探究】
(1)v-t图像中可利用图像斜率求_______。
(2)v-t图像中可利用面积求_____。
加速度
位移
【解析】选A、D。在0到2s末的时间内物体做匀加速
直线运动,加速度a=
m/s2=1m/s2,故A正确;
0~5s内物体的位移等于梯形面积s1=
×2×2m+2
×2m+
×1×2m=7m,故B错误;在5~6s内物体
的位移等于t轴下面三角形面积s2=-(
×1×1)m=
-0.5m,故0~6s内物体的位移s=s1+s2=6.5m,D正
确,C错误。
【误区警示】分析v-t图像的两大误区
(1)把v-t图像和s-t图像混淆不清。例如:把v-t图像中两条直线的交点误认为相遇,在s-t图像中根据直线向上倾斜、向下倾斜判断运动方向等等。
(2)把v-t图像误认为是质点的运动轨迹。v-t图像与坐标轴围成的图形的“面积”在横轴上方为“正”,在横轴下方为“负”;这“面积”的代数和表示对应时间内发生的位移,这“面积”的绝对值之和表示对应时间内的路程。
【素养训练】
1.(多选)甲、乙两个物体在同一地点,沿同一方向做直线运动的速度—时间图像如图所示,关于6s内甲、乙的运动说法正确的是( )
A.两物体相遇的时间是2s和6s
B.0~1s内甲在乙前面,1~4s内乙在甲前面
C.两个物体相距最远的时刻是4s末
D.4s时乙的加速度为-1m/s2
【解析】选A、C、D。在2s和6s时,甲、乙两物体图线与时间轴围成的面积相等,则位移相等,两物体相遇,故A正确;0~1s内甲的位移大于乙,则甲在乙前面,1~2s内甲仍在乙的前面,第2s时两者相遇;2~4内乙在甲前面,选项B错误;在0~2s内,两物体的距离先增大后减小,在1s时,速度相等,相距最远,最远距离Δs1=
×1×2m=1m,在2~6s内,两物体之间的距离先增大后减小,在4s时,速度相等,相距最远,最远距离Δs2=
×2×2m=2m,知4s末相距最远,故C正确;4s时乙的加速度为a=
m/s2=-1m/s2,选项D正确。
2.(多选)(2019·三明高一检测)甲、乙两个物体沿同一直线运动,它们的速度图像如图所示。由图像可知( )
A.甲运动时的加速度为-1m/s2
B.乙运动时的加速度为4m/s2
C.从开始计时到甲、乙速度相同的过程中,甲的位移为250m,乙的位移为50m
D.甲、乙沿相反方向运动
【解析】选A、B、C。在v-t图像中,图线的斜率表示
物体运动的加速度,故a甲=-1m/s2,故A正确;a乙=
m/s2=4m/s2,故B正确;图线与坐标轴围成的面
积表示物体运动的位移,速度相同时,s甲=
×(20+
30)×10m=250m,s乙=
×5×20m=50m,故C正确;
甲、乙两物体的速度都为正值,故运动方向相同,故D
错误。
【补偿训练】
1.甲、乙两个质点同时同地向同一方向做直线运动,它们的v-t图像如图所示,则( )
A.甲、乙运动方向相反
B.2s末乙追上甲
C.前4s内乙的平均速度大于甲的平均速度
D.乙追上甲时距出发点40m远
【解析】选D。甲、乙速度方向相同,二者运动方向相
同,选项A错误;2s末两质点的速度相等,但甲质点
的位移s甲=20m,乙质点的位移s乙=
m/s×2s=10m,选项B错误;在前4s内,甲的平均速度v甲=10m/s,乙的平均速度v乙=
m/s=10m/s,选项C错误;乙与甲的位移相等时,乙追上甲,此时两者发生的位移均为s=40m,选项D正确。
2.如图所示,A、B分别是甲、乙两小球从同一地点沿同一直线运动的v-t图像,根据图像可以判断( )
A.甲、乙两小球做初速度方向相反的匀减速直线运动,加速度大小相同,方向相反
B.两小球在t=8s时相距最远
C.两小球在t=2s时速度相同
D.两小球在t=8s时相遇
【解析】选D。甲、乙两球的初速度方向相反,加速度
与其初速度方向相反,甲小球的加速度为a甲=-10m/s2,乙小球的加速度为a乙=
m/s2,选项A错误;在t=8s
内,甲小球的位移s甲=0,8s时回到了初始位置,乙小
球的位移s乙=0,也在8s时回到了初始位置,因此,
在8s时两小球相遇,选项B错误,选项D正确;在t=2s时两小球的速度大小相等,但方向相反,两小球速度不相同,选项C错误。
三、位移、速度关系的应用
1.适用条件:
公式
=2as表述的是匀变速直线运动的速度与位移的关系,适用于匀变速直线运动。
2.意义:公式
=2as反映了初速度v0、末速度vt、加速度a、位移s之间的关系,当其中三个物理量已知时,可求另一个未知量。
3.公式的矢量性:
公式中v0、vt、a、s都是矢量,应用时必须选取统一的正方向,一般选v0方向为正方向。
(1)物体做加速运动时,a取正值,做减速运动时,a取负值。
(2)s>0,说明物体通过的位移方向与初速度方向相同;s<0,说明位移的方向与初速度的方向相反。
4.两种特殊形式:
(1)当v0=0时,
=2as(初速度为零的匀加速直线运动)
(2)当vt=0时,-
=2as(末速度为零的匀减速直线
运动)
【思考·讨论】
情境:
如图所示,狙击步枪射击时,若把子弹在枪筒中的运动看作是匀加速直线运动,假设枪筒长s,子弹的加速度为a。
讨论:(1)根据速度公式和位移公式求子弹射出枪口时
的速度。(科学思维)
提示:由s=
at2,vt=at得vt=
。
(2)在上面问题中,已知条件和所求的结果都不涉及时间t,它只是一个中间量,能否将两个公式联立,消去t,只用一个关系式表示位移s与速度vt的关系呢?(科学思维)
提示:vt=v0+at,把t=
代入
s=v0t+
at2得
=2as。
【典例示范】
如图是歼-15战机在“辽宁”号航母甲板上起飞的情形。假设“辽宁”号起飞甲板的长度为200m,降落甲板的长度为90m,歼-15战机起飞的最小速度为80m/s,战机在航母上的平均加速度为15m/s2。如果战机从静止开始做匀加速直线运动,战机在航母上能否正常起飞?
【解析】战机初速度为零,由位移与速度关系式得战机滑离甲板时的速度v=
m/s=20
m/s由于
20
m/s<80m/s所以战机不能正常起飞。
答案:战机不能正常起飞。
【规律方法】公式
=2as的应用技巧
(1)当物体做匀变速直线运动时,如果不涉及时间一般用速度位移公式较方便。
(2)刹车问题由于末速度为零,应用此公式往往较方便。
【母题追问】
1.在【典例示范】中,战机如果要在甲板上正常起飞,航母和战机要有一定的初速度,航母的初速度是多少?战机在航母上的运动时间是多少?(科学思维)
【解析】由位移与速度关系式v2-
=2as可得:
v0=
=20m/s,即航母以20m/s的速度航行。由速度公式v=v0+at可得运动时间t=
=4s。
答案:20m/s 4s
2.在【典例示范】中,战机在航母甲板上降落时的速度达到60m/s,为了使战机安全降落,航母上装有阻拦索,可以使战机在短距离内停止运动。如果航母静止,降落时在甲板上滑行的距离为90m。战机要安全降落,阻拦索对战机产生的加速度大小是多少?(科学思维)
【解析】战机的初速度v=60m/s,末速度为零,即v′=0,由位移与速度关系式得:a=
=
m/s2=-20m/s2。
答案:20m/s2
【拓展例题】机动车刹车类问题的处理
【典题示范】一辆汽车刹车前速度为90km/h,刹车时获得的加速度大小为10m/s2,求:
(1)汽车开始刹车后10s内滑行的距离s0。
(2)从开始刹车到汽车位移为30m所经历的时间t。
(3)汽车静止前1s内滑行的距离s′。
【解析】(1)先算出汽车刹车经历的总时间。
由题意可知,初速度v0=90km/h=25m/s,末速度vt=0
根据vt=v0+at0及a=-10m/s2得
t0=
=2.5s<10s
汽车刹车后经过2.5s停下来,因此汽车刹车后10s内
的位移等于2.5s内的位移,可用以下两种解法。
解法一:根据位移公式得
s0=v0t0+
=(25×2.5-
×10×2.52)m=31.25m
解法二:根据
=2as0得
s0=
m=31.25m。
(2)根据s=v0t+
at2得
解得t1=2s,t2=3s,t2表示汽车经t1后继续前进到达最远点后,再反向加速运动重新到达位移为30m处时所经历的时间,由于汽车刹车是单向运动,很显然,t2不合题意,应舍去。
(3)把汽车减速到速度为零的过程逆向看作初速度为零的匀加速运动,求出汽车以10m/s2的加速度经过1s的位移,
即s′=
a′t′2=
×10×12m=5m。
答案:(1)31.25m (2)2s (3)5m
【课堂回眸】
谢
谢
位移变化规律
一、匀变速直线运动位移—时间关系
1.位移在v-t图像中的表示:
(1)匀速运动:如图所示,在匀速直线运动中,v-t图像与t轴所围矩形“面积”表示_____。
位移
(2)匀变速直线运动:
①微元法推导。
a.把物体的运动分成几个小段,如图甲,每段位移≈
每段起始时刻速度×每段的时间=对应矩形面积。所
以,整个过程的位移≈各个小矩形面积_____。
之和
b.把运动过程分为更多的小段,如图乙,各小矩形的
_________可以更精确地表示物体在整个过程的位移。
面积之和
c.把整个过程分得非常非常细,如图丙,小矩形合在
一起成了一个梯形,___________就代表物体在相应时
间间隔内的位移。
梯形的面积
②结论:做匀变速直线运动的物体的位移对应着v-t图
像中的___________________所包围的梯形面积。
图线与对应的时间轴
2.位移公式的推导过程:
3.位移—时间图像(s-t图像):
(1)画法:以横轴表示_____、纵轴表示_____,根据实
际数据选单位、定标度、描点,用平滑曲线连接各点
便得到s-t图像。
时间
位移
(2)图像性质:对于匀变速直线运动来说,位移是时间
的_________,其图像是一条二次函数的部分曲线,如
图。
二次函数
二、匀变速直线运动的位移—速度关系
一、公式s=v0t+
at2的应用
1.各物理量的意义:公式中s表示时间t内物体运动的位移,单位是m;v0表示初速度,单位是m/s;a表示加速度,单位是m/s2;t表示运动时间,单位是s。
2.适用条件:公式反映了位移随时间的变化规律,公式仅适用于匀变速直线运动位移的求解。
3.符号规定:公式中s、v0、a都是矢量,应用时必须选取统一的正方向,一般选取初速度v0的方向为正方向。
(1)若a与v0同向,a取正值,物体做匀加速直线运动。
(2)若a与v0反向,a取负值,物体做匀减速直线运动。
(3)若位移的计算结果为正值,说明这段时间内位移的
方向与规定的正方向相同。
(4)若位移的计算结果为负值,说明这段时间内位移的
方向与规定的正方向相反。
4.若v0=0,则s=
at2,位移与时间的二次方成正比。
【思考·讨论】
利用公式s=v0t+
at2求出的位移大小等于物体运动的
路程吗?(科学思维)
提示:不一定,当物体匀减速运动到速度为零再反向
以等大的加速度匀加速运动时,位移的大小小于路程。
【典例示范】
(2019·福州高一检测)一辆卡车初速度为v0=10m/s,以a=2m/s2的加速度行驶,求:
(1)卡车在3s末的速度大小v3。
(2)卡车在6s内的位移大小s6。
(3)卡车在第6s内的位移大小sⅥ。
【解题探究】
(1)3s末是时刻还是时间?
提示:3s末是一个瞬时,是时刻。
(2)“第6s内”是多长时间?“第6s内”的位移是6s内的总位移吗?
提示:“第6s内”是指1s的时间,其位移为第六个1s内的位移,不是6s内的总位移。
【解析】(1)卡车在3s末的速度为v3=v0+at3=(10+2×
3)m/s=16m/s。
(2)卡车在6s内的位移为s6=v0t6+
=(10×6+
×
2×36)m=96m。
(3)卡车在第6s内的位移为sⅥ=s6-s5=s6-(v0t5+
)
=96m-(10×5+
×2×25)m=21m。
答案:(1)16m/s (2)96m (3)21m
【误区警示】应用位移公式的两点注意
(1)公式s=v0t+
at2仅适用于匀变速直线运动。
(2)应用位移公式解题时常选初速度的方向为正方向,
物体若加速则加速度为正值,减速则加速度为负值。
【素养训练】
1.(多选)(2019·厦门高一检测)物体从静止开始做匀加速直线运动,第3s内通过的位移是3m,则( )
A.前3s的位移是6m
B.3s末的速度是3.6m/s
C.3s内的平均速度是2m/s
D.第5s内的平均速度是5.4m/s
【解析】选B、D。由位移公式s=
at2知,第3s内的
位移为
a×32m-a×
22m=3m,故加速度a=1.2m/s2,
所以前3s的位移s=
×1.2×32m=5.4m,A错误;
第3s末的速度v=at=1.2×3m/s=3.6m/s,B正确;
3s内的平均速度
=1.8m/s,C错误;
第5s内的平均速度等于第4.5s末的瞬时速度,
故v′=at′=1.2×4.5m/s=5.4m/s,D正确。
2.从静止开始做匀加速直线运动的汽车,经过t=10s,走过位移s=30m。求:
(1)汽车运动的加速度大小。
(2)汽车10s末的速度。
【解析】(1)根据匀变速直线运动位移公式得,
s=
at2,代入数据解得a=
=0.6m/s2。
(2)根据匀变速直线运动速度公式得汽车10s末的速
度v=at=6m/s。
答案:(1)0.6m/s2 (2)6m/s
【补偿训练】
1.以10m/s的速度行驶的列车,在下坡路上的加速度为0.2m/s2,经过30s到达坡底。求:
(1)到达坡底的速度。
(2)坡路的长度。
【解析】(1)根据速度公式,得列车到达坡底的速度为
vt=v0+at=10m/s+0.2×30m/s=16m/s
(2)根据位移公式得坡路的长度为
s=v0t+
at2=10×30m+
×0.2×302m=390m
答案:(1)16m/s (2)390m
2.一辆汽车在平直公路上做匀变速直线运动,公路边每隔15m有一棵树,如图所示,汽车通过A、B两相邻的树用了3s,通过B、C两相邻的树用了2s,求汽车运动的加速度大小和通过树B时的速度大小。
【解析】设汽车经过树A时速度为vA,加速度为a。对AB段运动,由s=v0t+
at2有:15m=vA×3s+a×
(3s)2
同理,对AC段运动,有:30m=vA×5s+a×
(5s)2
两式联立解得:vA=3.5m/s,a=1m/s2
再由速度公式vt=v0+at得:vB=3.5m/s+1m/s2×3s=6.5m/s
答案:1m/s2 6.5m/s
二、用v-t图像求位移
1.匀速直线运动的位移:
(1)做匀速直线运动的物体在时间t内的位移s=vt。
(2)做匀速直线运动的物体,其v-t图像是一条平行于时间轴的直线,其位移在数值上等于v-t图线与对应的时间轴所包围的矩形的面积。如图所示。
2.匀变速直线运动的位移:
(1)如图所示,图线与时间轴所围的梯形的面积就代表
物体在时间t内的位移,梯形的上底为v0,下底为v,
对应的时间为t,则有:s=(v0+v)t。
(2)因为t时刻的速度v=v0+at,所以位移与时间的关系
为s=
(v0+v0+at)t=v0t+
at2。
【典例示范】
(多选)(2019·龙岩高一检测)某物体运动的v-t图像如图所示,根据图像可知,该物体( )
A.在0到2s末的时间内,加速度为1m/s2
B.在0到5s末的时间内,位移为10m
C.在0到6s末的时间内,位移为7.5m
D.在0到6s末的时间内,位移为6.5m
【解题探究】
(1)v-t图像中可利用图像斜率求_______。
(2)v-t图像中可利用面积求_____。
加速度
位移
【解析】选A、D。在0到2s末的时间内物体做匀加速
直线运动,加速度a=
m/s2=1m/s2,故A正确;
0~5s内物体的位移等于梯形面积s1=
×2×2m+2
×2m+
×1×2m=7m,故B错误;在5~6s内物体
的位移等于t轴下面三角形面积s2=-(
×1×1)m=
-0.5m,故0~6s内物体的位移s=s1+s2=6.5m,D正
确,C错误。
【误区警示】分析v-t图像的两大误区
(1)把v-t图像和s-t图像混淆不清。例如:把v-t图像中两条直线的交点误认为相遇,在s-t图像中根据直线向上倾斜、向下倾斜判断运动方向等等。
(2)把v-t图像误认为是质点的运动轨迹。v-t图像与坐标轴围成的图形的“面积”在横轴上方为“正”,在横轴下方为“负”;这“面积”的代数和表示对应时间内发生的位移,这“面积”的绝对值之和表示对应时间内的路程。
【素养训练】
1.(多选)甲、乙两个物体在同一地点,沿同一方向做直线运动的速度—时间图像如图所示,关于6s内甲、乙的运动说法正确的是( )
A.两物体相遇的时间是2s和6s
B.0~1s内甲在乙前面,1~4s内乙在甲前面
C.两个物体相距最远的时刻是4s末
D.4s时乙的加速度为-1m/s2
【解析】选A、C、D。在2s和6s时,甲、乙两物体图线与时间轴围成的面积相等,则位移相等,两物体相遇,故A正确;0~1s内甲的位移大于乙,则甲在乙前面,1~2s内甲仍在乙的前面,第2s时两者相遇;2~4内乙在甲前面,选项B错误;在0~2s内,两物体的距离先增大后减小,在1s时,速度相等,相距最远,最远距离Δs1=
×1×2m=1m,在2~6s内,两物体之间的距离先增大后减小,在4s时,速度相等,相距最远,最远距离Δs2=
×2×2m=2m,知4s末相距最远,故C正确;4s时乙的加速度为a=
m/s2=-1m/s2,选项D正确。
2.(多选)(2019·三明高一检测)甲、乙两个物体沿同一直线运动,它们的速度图像如图所示。由图像可知( )
A.甲运动时的加速度为-1m/s2
B.乙运动时的加速度为4m/s2
C.从开始计时到甲、乙速度相同的过程中,甲的位移为250m,乙的位移为50m
D.甲、乙沿相反方向运动
【解析】选A、B、C。在v-t图像中,图线的斜率表示
物体运动的加速度,故a甲=-1m/s2,故A正确;a乙=
m/s2=4m/s2,故B正确;图线与坐标轴围成的面
积表示物体运动的位移,速度相同时,s甲=
×(20+
30)×10m=250m,s乙=
×5×20m=50m,故C正确;
甲、乙两物体的速度都为正值,故运动方向相同,故D
错误。
【补偿训练】
1.甲、乙两个质点同时同地向同一方向做直线运动,它们的v-t图像如图所示,则( )
A.甲、乙运动方向相反
B.2s末乙追上甲
C.前4s内乙的平均速度大于甲的平均速度
D.乙追上甲时距出发点40m远
【解析】选D。甲、乙速度方向相同,二者运动方向相
同,选项A错误;2s末两质点的速度相等,但甲质点
的位移s甲=20m,乙质点的位移s乙=
m/s×2s=10m,选项B错误;在前4s内,甲的平均速度v甲=10m/s,乙的平均速度v乙=
m/s=10m/s,选项C错误;乙与甲的位移相等时,乙追上甲,此时两者发生的位移均为s=40m,选项D正确。
2.如图所示,A、B分别是甲、乙两小球从同一地点沿同一直线运动的v-t图像,根据图像可以判断( )
A.甲、乙两小球做初速度方向相反的匀减速直线运动,加速度大小相同,方向相反
B.两小球在t=8s时相距最远
C.两小球在t=2s时速度相同
D.两小球在t=8s时相遇
【解析】选D。甲、乙两球的初速度方向相反,加速度
与其初速度方向相反,甲小球的加速度为a甲=-10m/s2,乙小球的加速度为a乙=
m/s2,选项A错误;在t=8s
内,甲小球的位移s甲=0,8s时回到了初始位置,乙小
球的位移s乙=0,也在8s时回到了初始位置,因此,
在8s时两小球相遇,选项B错误,选项D正确;在t=2s时两小球的速度大小相等,但方向相反,两小球速度不相同,选项C错误。
三、位移、速度关系的应用
1.适用条件:
公式
=2as表述的是匀变速直线运动的速度与位移的关系,适用于匀变速直线运动。
2.意义:公式
=2as反映了初速度v0、末速度vt、加速度a、位移s之间的关系,当其中三个物理量已知时,可求另一个未知量。
3.公式的矢量性:
公式中v0、vt、a、s都是矢量,应用时必须选取统一的正方向,一般选v0方向为正方向。
(1)物体做加速运动时,a取正值,做减速运动时,a取负值。
(2)s>0,说明物体通过的位移方向与初速度方向相同;s<0,说明位移的方向与初速度的方向相反。
4.两种特殊形式:
(1)当v0=0时,
=2as(初速度为零的匀加速直线运动)
(2)当vt=0时,-
=2as(末速度为零的匀减速直线
运动)
【思考·讨论】
情境:
如图所示,狙击步枪射击时,若把子弹在枪筒中的运动看作是匀加速直线运动,假设枪筒长s,子弹的加速度为a。
讨论:(1)根据速度公式和位移公式求子弹射出枪口时
的速度。(科学思维)
提示:由s=
at2,vt=at得vt=
。
(2)在上面问题中,已知条件和所求的结果都不涉及时间t,它只是一个中间量,能否将两个公式联立,消去t,只用一个关系式表示位移s与速度vt的关系呢?(科学思维)
提示:vt=v0+at,把t=
代入
s=v0t+
at2得
=2as。
【典例示范】
如图是歼-15战机在“辽宁”号航母甲板上起飞的情形。假设“辽宁”号起飞甲板的长度为200m,降落甲板的长度为90m,歼-15战机起飞的最小速度为80m/s,战机在航母上的平均加速度为15m/s2。如果战机从静止开始做匀加速直线运动,战机在航母上能否正常起飞?
【解析】战机初速度为零,由位移与速度关系式得战机滑离甲板时的速度v=
m/s=20
m/s由于
20
m/s<80m/s所以战机不能正常起飞。
答案:战机不能正常起飞。
【规律方法】公式
=2as的应用技巧
(1)当物体做匀变速直线运动时,如果不涉及时间一般用速度位移公式较方便。
(2)刹车问题由于末速度为零,应用此公式往往较方便。
【母题追问】
1.在【典例示范】中,战机如果要在甲板上正常起飞,航母和战机要有一定的初速度,航母的初速度是多少?战机在航母上的运动时间是多少?(科学思维)
【解析】由位移与速度关系式v2-
=2as可得:
v0=
=20m/s,即航母以20m/s的速度航行。由速度公式v=v0+at可得运动时间t=
=4s。
答案:20m/s 4s
2.在【典例示范】中,战机在航母甲板上降落时的速度达到60m/s,为了使战机安全降落,航母上装有阻拦索,可以使战机在短距离内停止运动。如果航母静止,降落时在甲板上滑行的距离为90m。战机要安全降落,阻拦索对战机产生的加速度大小是多少?(科学思维)
【解析】战机的初速度v=60m/s,末速度为零,即v′=0,由位移与速度关系式得:a=
=
m/s2=-20m/s2。
答案:20m/s2
【拓展例题】机动车刹车类问题的处理
【典题示范】一辆汽车刹车前速度为90km/h,刹车时获得的加速度大小为10m/s2,求:
(1)汽车开始刹车后10s内滑行的距离s0。
(2)从开始刹车到汽车位移为30m所经历的时间t。
(3)汽车静止前1s内滑行的距离s′。
【解析】(1)先算出汽车刹车经历的总时间。
由题意可知,初速度v0=90km/h=25m/s,末速度vt=0
根据vt=v0+at0及a=-10m/s2得
t0=
=2.5s<10s
汽车刹车后经过2.5s停下来,因此汽车刹车后10s内
的位移等于2.5s内的位移,可用以下两种解法。
解法一:根据位移公式得
s0=v0t0+
=(25×2.5-
×10×2.52)m=31.25m
解法二:根据
=2as0得
s0=
m=31.25m。
(2)根据s=v0t+
at2得
解得t1=2s,t2=3s,t2表示汽车经t1后继续前进到达最远点后,再反向加速运动重新到达位移为30m处时所经历的时间,由于汽车刹车是单向运动,很显然,t2不合题意,应舍去。
(3)把汽车减速到速度为零的过程逆向看作初速度为零的匀加速运动,求出汽车以10m/s2的加速度经过1s的位移,
即s′=
a′t′2=
×10×12m=5m。
答案:(1)31.25m (2)2s (3)5m
【课堂回眸】
谢
谢
同课章节目录
- 绪论 撩开物理学的神秘面纱
- 一、源自然之问
- 二、探万物之秘
- 三、采科学之益
- 四、启智慧之迪
- 第1章 运动的描述
- 第1节 空间和时间
- 第2节 质点和位移
- 第3节 速度
- 第4节 加速度
- 第2章 匀变速直线运动
- 第1节 速度变化规律
- 第2节 位移变化规律
- 第3节 实验中的误差和有效数字
- 第4节 科学测量:做直线运动物体的瞬时速度
- 第5节 自由落体运动
- 第3章 相互作用
- 第1节 重力与重心
- 第2节 科学探究:弹力
- 第3节 摩擦力
- 第4章 力与平衡
- 第1节 科学探究:力的合成
- 第2节 力的分解
- 第3节 共点力的平衡
- 第5章 牛顿运动定律
- 第1节 牛顿第一运动定律
- 第2节 科学探究:加速度与力、质量的关系
- 第3节 牛顿第二运动定律
- 第4节 牛顿第三运动定律
- 第5节 超重与失重
