鲁教版(五四制)七上 4.1无理数 (28张PPT)
文档属性
| 名称 | 鲁教版(五四制)七上 4.1无理数 (28张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 715.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-02 00:00:00 | ||
图片预览






文档简介
(共28张PPT)
4.1无理数
整数
正整数:如:1,2,3,…
零:0
负整数:如-1,-2,-3,…
分数
正分数:如
,
,
5.2,
…
负分数如
,
,-3.5,
…
有理数
回顾
&
思考
?
什么叫有理数?
3.除了有理数外还有没有其他的数呢?
返
回
1.回顾从小学到现在我们都学过哪些数?
统称有理数
请大家把下列各数表示成小数.
3=
=
=
=
总结:上面这些数都是有理数,它们总可以用
.
小数或
小数表示.反过来,任何有限小数或无限循环小数都是有理数.
3.0
0.8
有限
无限循环
【温故知新】
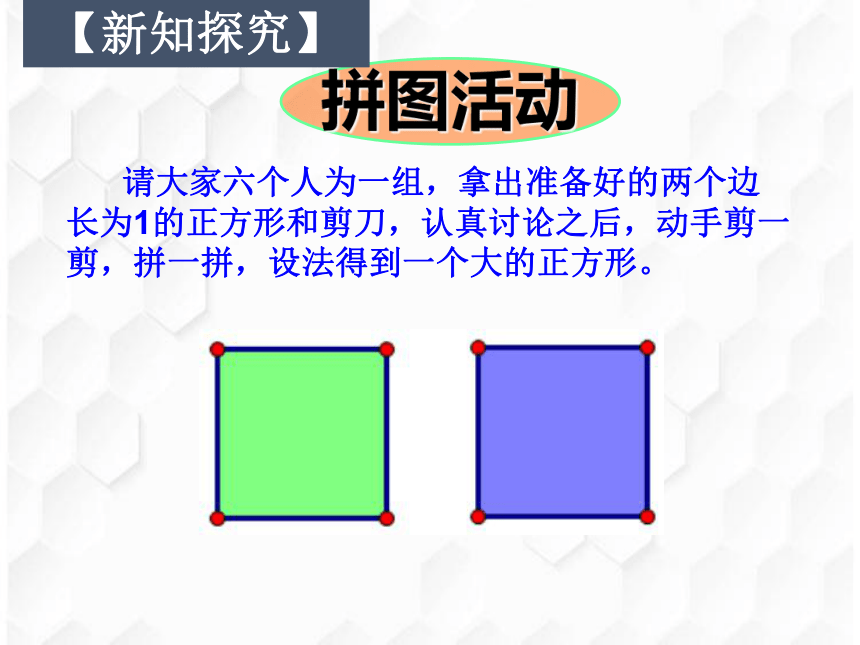
拼图活动
请大家六个人为一组,拿出准备好的两个边长为1的正方形和剪刀,认真讨论之后,动手剪一剪,拼一拼,设法得到一个大的正方形。
【新知探究】
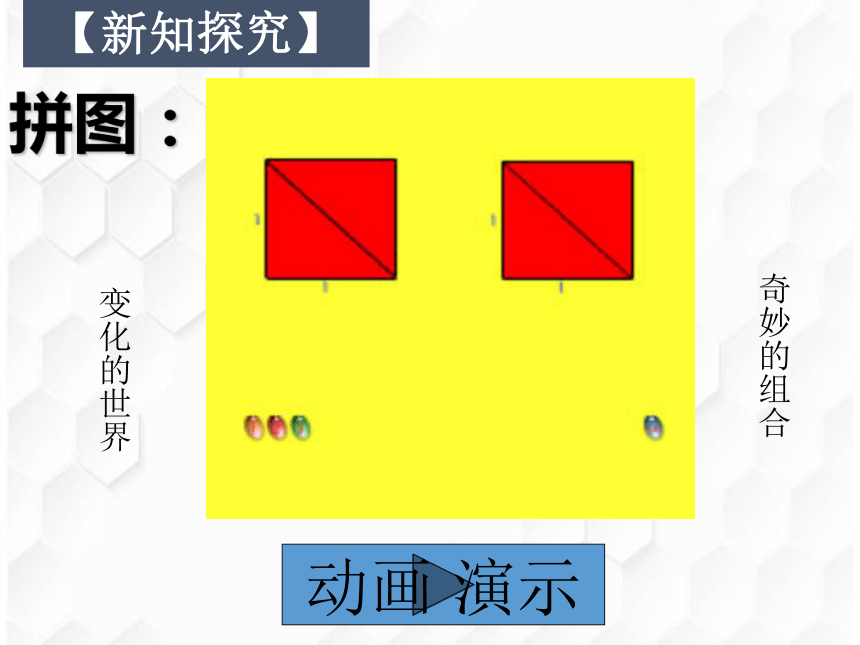
1
1
变化的世界
奇妙的组合
拼图:
动画
演示
【新知探究】
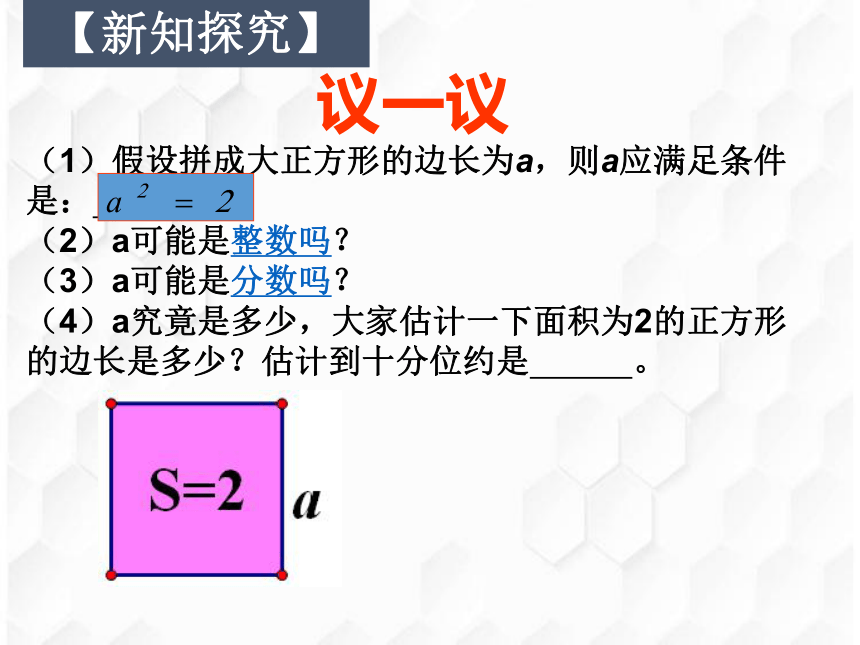
议一议
(1)假设拼成大正方形的边长为a,则a应满足条件是:
。
(2)a可能是整数吗?
(3)a可能是分数吗?
(4)a究竟是多少,大家估计一下面积为2的正方形的边长是多少?估计到十分位约是
。
【新知探究】
越来越大,
所以a不可能是整数
(2)a可能是整数吗?
【新知探究】
(3)a可能是以2为分母的分数吗?
结果都为分数,所以a不可能是以2为分母的分数。
【新知探究】
(3)a可能是以3为分母的分数吗?
结果都为分数,所以a不可能是以3为分母的分数。
【新知探究】
(3)a可能是分数吗?
试说出原因。
两个相同的最简分数的乘积仍然是分数,所以a不可能是分数。
【新知探究】
a既不是整数又不是分数,所以a一定不是
。
有理数
【新知探究】
(4)a究竟是多少,大家估计一下面积为2的正方形的边长是多少?估计到十分位约是
。
1.4
【新知探究】
想一想
在下图中,以直角三角形的斜边为边的正方形的面积是
,设该正方形的边长为b,b应满足的条件是
,b是有理数吗?
5
b2=5
b既不是整数又不是分数,所以b一定不是有理数。
b是什么数呢?
有理数已经不够用了!
【新知探究】
利用计算器(电脑)探究:以上问题中的a、b到底是什么数呢?
我们借助计算机进行探究
【引入新数】
边长a
面积s
111.41.961.411.98811.4141.9993961.41421.99996164还可以继续算下去吗?a可能是有限小数吗?
事实上,a=1.41421356……,是一个无限不循环小数
事实上,b=2.236067978…,也是一个无限不循环小数
【引入新数】
像1.41421356…,2.2360679…等这些数的小数位数都是无限的,但是又不是循环的,
是无限不循环小数.
无限不循环小数叫无理数.
(圆周率π=3.14159265…也是一个无限不循环小数,故π是无理数)
有理数总可以用有限小数或无限循环小数表示。
反过来,任何有限小数或无限循环小数也都是有理数。
【引入新数】
希伯索斯(Hippasus)
毕达哥拉斯的学生
请阅读课本第36页读一读
真理毕竟是淹没不了的。
真理是经得起时间的考验的!
人们不会忘记希伯索斯这位为真理而献身的可敬学者,还把这样的数取名为“无理数”。
你还可以上网搜索关于无理数的知识!
无理数的发现
【引入新数】
三、分一分
到目前为止我们所学过的数可以分为几类?
按小数的形式来分
有理数:有限小数或无限循环小数
无理数:无限不循环小数
数
整数
分数
【引入新数】
四、辨一辨
例1
下列数哪些是有理数?
哪些是无理数?
3.14159,
-5.2323323332…,
0.585885888588885
123.34567891011…(由相继的正整数组成).
面积为8的正方形的边长m
?
无理数的常见类型有哪些?
【引入新数】
以下各正方形的边长是无理数的是(
)
A.面积为25的正方形;
B.面积为
的正方形;
C.面积为8的正方形;
D.面积为1.44的正方形.
C
例2
例3.填空.
1、面积是25的正方形的边长为
,它
是
数。
面积为7
的正方形边长a的整数部分是
,边长a是一个
数
2、如果x2=10,则x是一个
数
,x的整数部
分是
。
5
有理
2
无理
无理
3
(1)有限小数是有理数;
(
)
(2)无限小数都是无理数;
(
)
(3)无理数都是无限小数;
(
)
(4)有理数是有限小数.
(
)
(5)无限不循环小数是无理数.
(
)
例4
判断题
╳
√
√
╳
√
1.无理数是无限不循环小数,有理数是有限小数或
无限循环小数.
2.任何一个有理数都可以化成分数
形式(
p,q
为整数且互质),而无理数不能.
强
调
练一练:
1.如图,正三角形的边长为2,高为h,h可能是
整数吗?可能是分数吗?
C
B
A
D
h不可能是整数;
h也不可能是分数。
本课小结:
4.数的分类.
3.判定一个数是无理数还是有理数.
我们知道整数不够用就产生了分数,正数不够用就产生了负数,现在有理数不够用了,就要产生一种新数——无理数
1.在生活中确实存在既不是整数也不是分数的数,
既不是有理数的数。
2.无理数在现实生活中是大量存在的。
数够用了吗?
再见!!!
生活中有很多不是有理数的数
右图是由16个边长为1的小正方形拼成的,任意连接这些小正方形的若干个顶点,可得到一些线段。试分别找出一条长度是有理数的线段和一条长度不是有理数的线段。
画
图
由勾股定理知:
线段AC,CE,BE的长
不能用有理数表示。
例如:
线段AB,DE,AE的长
能用有理数表示;
4.1无理数
整数
正整数:如:1,2,3,…
零:0
负整数:如-1,-2,-3,…
分数
正分数:如
,
,
5.2,
…
负分数如
,
,-3.5,
…
有理数
回顾
&
思考
?
什么叫有理数?
3.除了有理数外还有没有其他的数呢?
返
回
1.回顾从小学到现在我们都学过哪些数?
统称有理数
请大家把下列各数表示成小数.
3=
=
=
=
总结:上面这些数都是有理数,它们总可以用
.
小数或
小数表示.反过来,任何有限小数或无限循环小数都是有理数.
3.0
0.8
有限
无限循环
【温故知新】
拼图活动
请大家六个人为一组,拿出准备好的两个边长为1的正方形和剪刀,认真讨论之后,动手剪一剪,拼一拼,设法得到一个大的正方形。
【新知探究】
1
1
变化的世界
奇妙的组合
拼图:
动画
演示
【新知探究】
议一议
(1)假设拼成大正方形的边长为a,则a应满足条件是:
。
(2)a可能是整数吗?
(3)a可能是分数吗?
(4)a究竟是多少,大家估计一下面积为2的正方形的边长是多少?估计到十分位约是
。
【新知探究】
越来越大,
所以a不可能是整数
(2)a可能是整数吗?
【新知探究】
(3)a可能是以2为分母的分数吗?
结果都为分数,所以a不可能是以2为分母的分数。
【新知探究】
(3)a可能是以3为分母的分数吗?
结果都为分数,所以a不可能是以3为分母的分数。
【新知探究】
(3)a可能是分数吗?
试说出原因。
两个相同的最简分数的乘积仍然是分数,所以a不可能是分数。
【新知探究】
a既不是整数又不是分数,所以a一定不是
。
有理数
【新知探究】
(4)a究竟是多少,大家估计一下面积为2的正方形的边长是多少?估计到十分位约是
。
1.4
【新知探究】
想一想
在下图中,以直角三角形的斜边为边的正方形的面积是
,设该正方形的边长为b,b应满足的条件是
,b是有理数吗?
5
b2=5
b既不是整数又不是分数,所以b一定不是有理数。
b是什么数呢?
有理数已经不够用了!
【新知探究】
利用计算器(电脑)探究:以上问题中的a、b到底是什么数呢?
我们借助计算机进行探究
【引入新数】
边长a
面积s
1
事实上,a=1.41421356……,是一个无限不循环小数
事实上,b=2.236067978…,也是一个无限不循环小数
【引入新数】
像1.41421356…,2.2360679…等这些数的小数位数都是无限的,但是又不是循环的,
是无限不循环小数.
无限不循环小数叫无理数.
(圆周率π=3.14159265…也是一个无限不循环小数,故π是无理数)
有理数总可以用有限小数或无限循环小数表示。
反过来,任何有限小数或无限循环小数也都是有理数。
【引入新数】
希伯索斯(Hippasus)
毕达哥拉斯的学生
请阅读课本第36页读一读
真理毕竟是淹没不了的。
真理是经得起时间的考验的!
人们不会忘记希伯索斯这位为真理而献身的可敬学者,还把这样的数取名为“无理数”。
你还可以上网搜索关于无理数的知识!
无理数的发现
【引入新数】
三、分一分
到目前为止我们所学过的数可以分为几类?
按小数的形式来分
有理数:有限小数或无限循环小数
无理数:无限不循环小数
数
整数
分数
【引入新数】
四、辨一辨
例1
下列数哪些是有理数?
哪些是无理数?
3.14159,
-5.2323323332…,
0.585885888588885
123.34567891011…(由相继的正整数组成).
面积为8的正方形的边长m
?
无理数的常见类型有哪些?
【引入新数】
以下各正方形的边长是无理数的是(
)
A.面积为25的正方形;
B.面积为
的正方形;
C.面积为8的正方形;
D.面积为1.44的正方形.
C
例2
例3.填空.
1、面积是25的正方形的边长为
,它
是
数。
面积为7
的正方形边长a的整数部分是
,边长a是一个
数
2、如果x2=10,则x是一个
数
,x的整数部
分是
。
5
有理
2
无理
无理
3
(1)有限小数是有理数;
(
)
(2)无限小数都是无理数;
(
)
(3)无理数都是无限小数;
(
)
(4)有理数是有限小数.
(
)
(5)无限不循环小数是无理数.
(
)
例4
判断题
╳
√
√
╳
√
1.无理数是无限不循环小数,有理数是有限小数或
无限循环小数.
2.任何一个有理数都可以化成分数
形式(
p,q
为整数且互质),而无理数不能.
强
调
练一练:
1.如图,正三角形的边长为2,高为h,h可能是
整数吗?可能是分数吗?
C
B
A
D
h不可能是整数;
h也不可能是分数。
本课小结:
4.数的分类.
3.判定一个数是无理数还是有理数.
我们知道整数不够用就产生了分数,正数不够用就产生了负数,现在有理数不够用了,就要产生一种新数——无理数
1.在生活中确实存在既不是整数也不是分数的数,
既不是有理数的数。
2.无理数在现实生活中是大量存在的。
数够用了吗?
再见!!!
生活中有很多不是有理数的数
右图是由16个边长为1的小正方形拼成的,任意连接这些小正方形的若干个顶点,可得到一些线段。试分别找出一条长度是有理数的线段和一条长度不是有理数的线段。
画
图
由勾股定理知:
线段AC,CE,BE的长
不能用有理数表示。
例如:
线段AB,DE,AE的长
能用有理数表示;
