24.1.4 圆周角 课件(共20张PPT)
文档属性
| 名称 | 24.1.4 圆周角 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-04 08:23:15 | ||
图片预览


文档简介
(共20张PPT)
24.1.4
圆周角
人教版
九年级上册
.
O
A
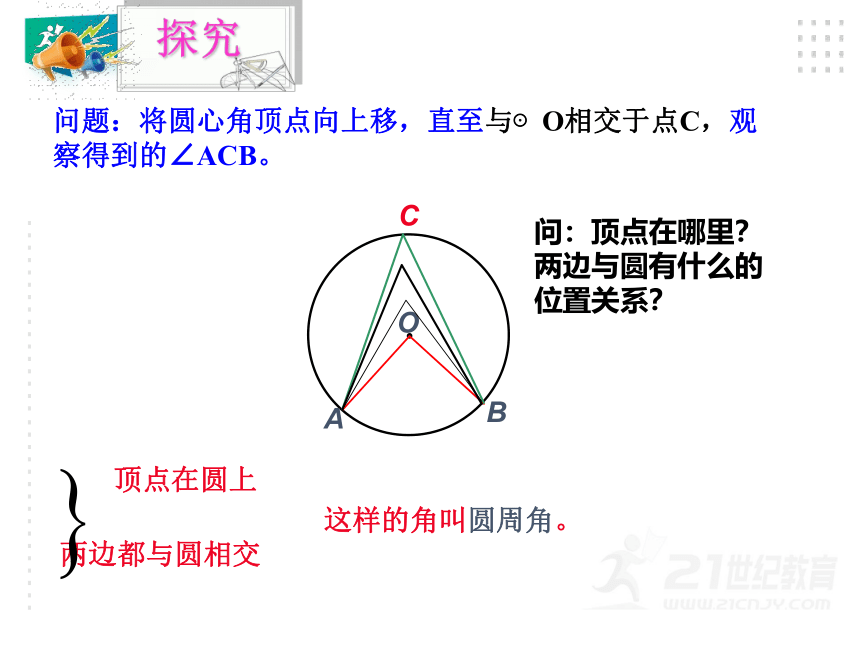
问题:将圆心角顶点向上移,直至与⊙O相交于点C,观察得到的∠ACB。
C
顶点在圆上
两边都与圆相交
这样的角叫圆周角。
B
问:顶点在哪里?两边与圆有什么的位置关系?
探究
E
.
O
B
C
A
.
O
B
C
D
.
O
B
C
A
试一试
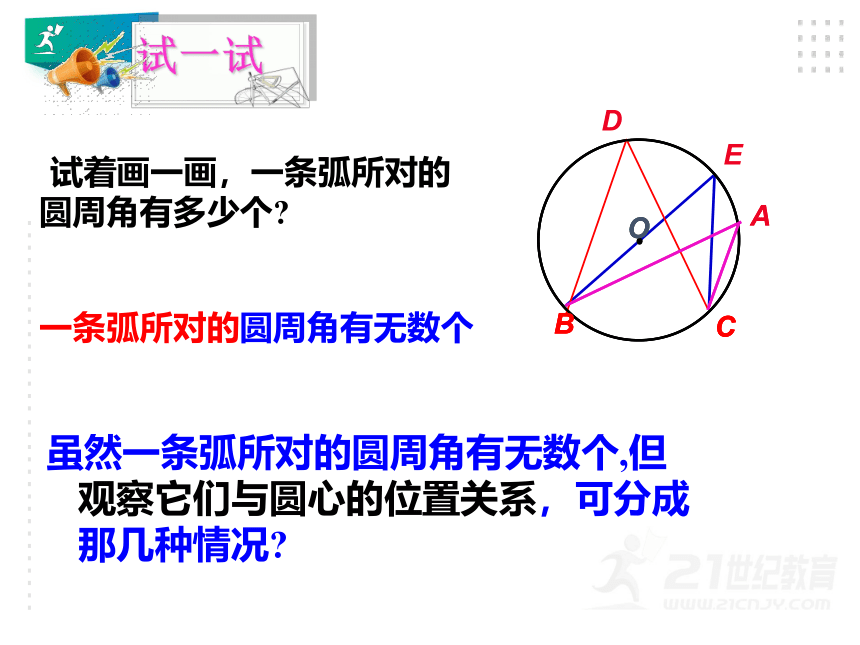
试着画一画,一条弧所对的圆周角有多少个?
一条弧所对的圆周角有无数个
虽然一条弧所对的圆周角有无数个,但观察它们与圆心的位置关系,可分成那几种情况?
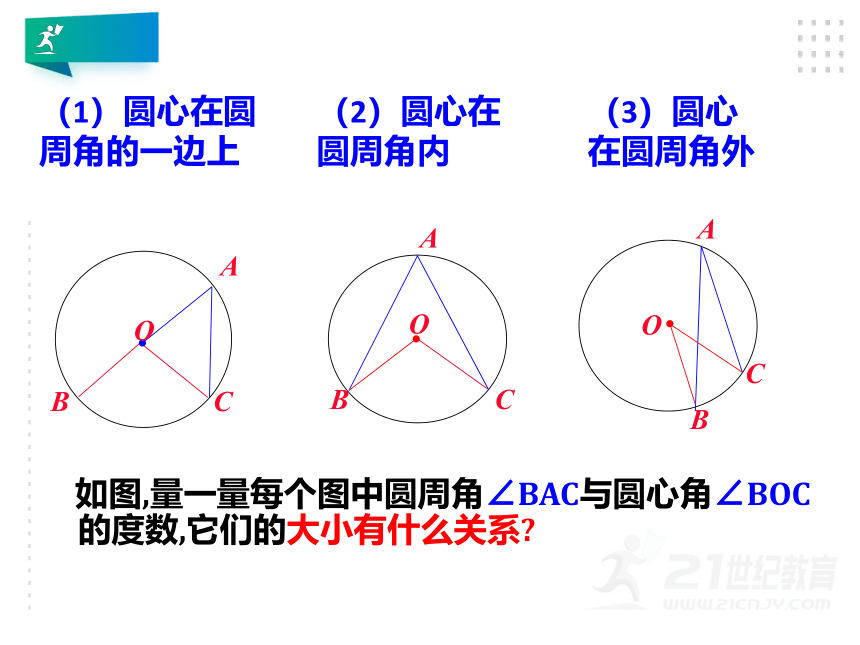
(3)圆心在圆周角外
(1)圆心在圆周角的一边上
(2)圆心在圆周角内
如图,量一量每个图中圆周角∠BAC与圆心角∠BOC的度数,它们的大小有什么关系?
A
B
C
O
A
B
C
O
A
B
C
O
1.第一种情况:圆心在角的一边上
A
B
C
O
∵
OA=OC
∴∠A=∠OCA
又
∠BOC=∠A+∠OCA
∴∠BOC=2∠A
即∠A=
∠BOC
一条弧所对的圆周角等于这条弧所对的圆心角的度数的一半。
猜想并证明
A
B
C
O
D
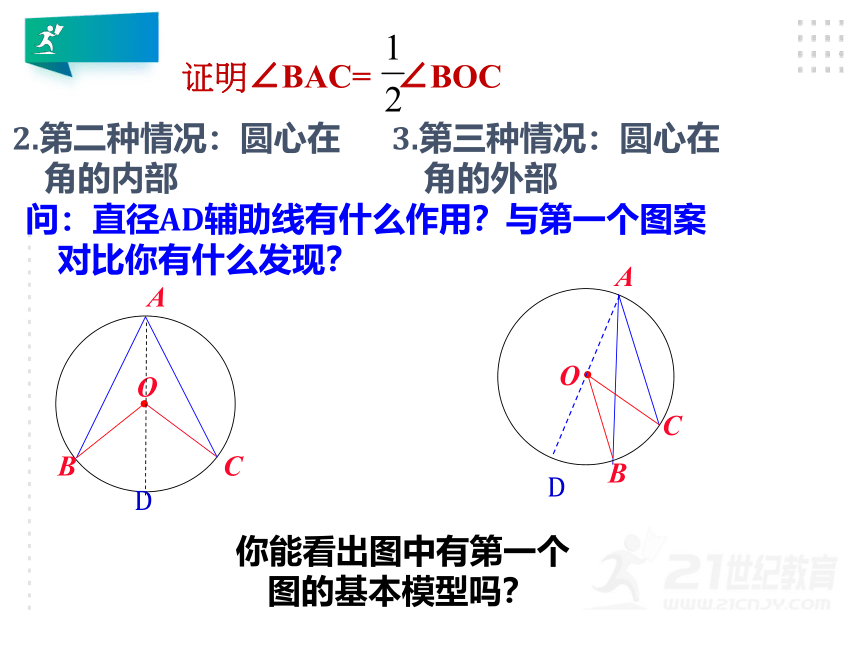
2.第二种情况:圆心在角的内部
问:直径AD辅助线有什么作用?与第一个图案对比你有什么发现?
3.第三种情况:圆心在角的外部
A
B
C
O
D
你能看出图中有第一个图的基本模型吗?
证明∠BAC=
∠BOC
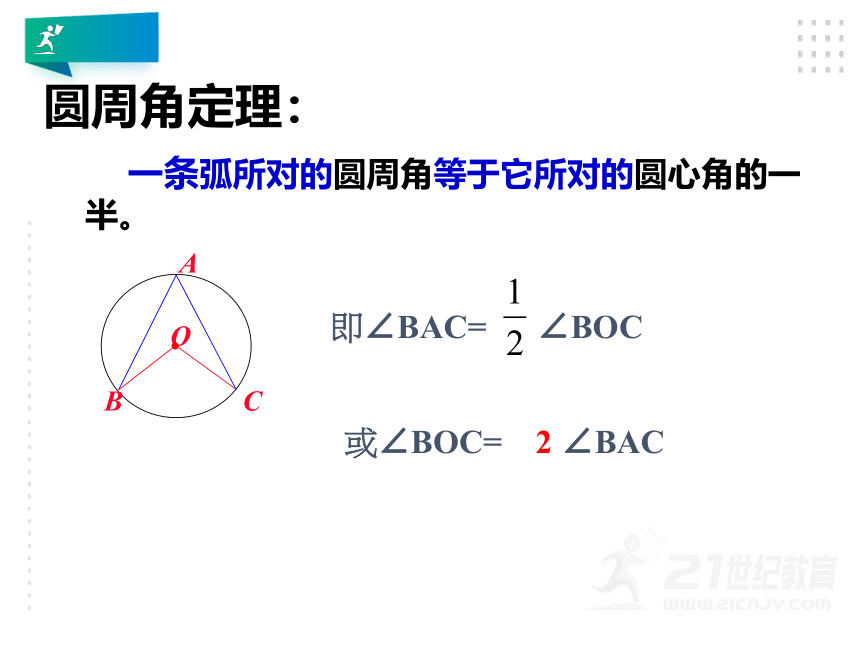
圆周角定理:
一条弧所对的圆周角等于它所对的圆心角的一半。
A
B
C
O
即∠BAC=
∠BOC
或∠BOC=
2
∠BAC
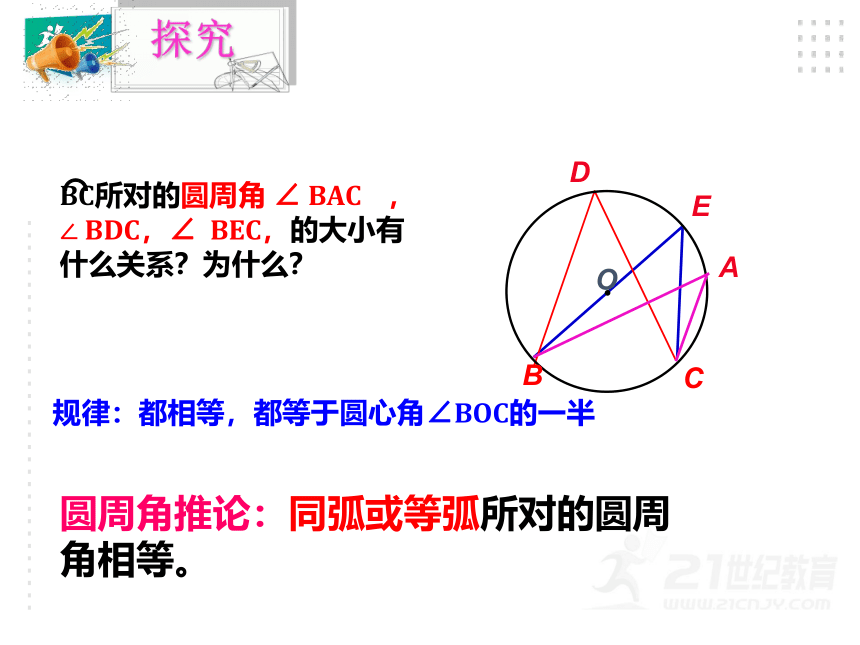
BC所对的圆周角
∠
BAC
,∠
BDC,∠
BEC,的大小有什么关系?为什么?
⌒
规律:都相等,都等于圆心角∠BOC的一半
圆周角推论:同弧或等弧所对的圆周角相等。
探究
E
D
.
O
B
C
A
推论1:同圆或等圆中,相等的圆周角所对的弧也相等。
D
A
B
O
C
E
F
F
∵
∠CAD=∠EBF
∴
CD=EF
)
)
推论2:半圆(或直径)所对的圆周角是直角,900的圆周角所对的弦是直径。
A
O
B
C1
C2
C3
∵
AB是直径
∴
∠AC1B=900
∵
∠AC1B=900
∴
AB是直径
新课讲解:
若一个多边形各顶点都在同一个圆上,那么,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆。
O
B
C
D
E
F
A
O
A
C
D
E
B
O
C
A
B
D
如图,
四边形ABCD为⊙O的内接四边形;
⊙O为四边形ABCD的外接圆。
思考:
∠A与∠C有什么关系?
∠B与∠D有什么关系?
C
O
D
B
A
如图:圆内接四边形ABCD中,
∵
弧BCD和弧BAD所对的圆心角的和是周角
∴∠A+∠C=
360°÷2=
180°
同理∠B+∠D=180°
结论:圆的内接四边形的对角互补。
符号表达式:
∵四边形ABCD是⊙O的内接四边形,
∴
∠A+∠C=180°
∠B+∠D=180°
O
C
A
B
D
圆的内接四边形的性质:
圆的内接四边形的对角互补。
3、圆周角定理的推论:
同圆或等圆中,同弧或等弧所对的圆周角相等;
用于找相等的角
一条弧所对的圆周角等于它所对的圆心角的一半。
2、圆周角定理:
1、圆周角定义:顶点在圆上,并且两边都和圆相交的角叫圆周角.
小结
小结
从特殊到一般的数学方法
转化思想(化归思想)
6、数学思想和方法:
分类讨论思想
4.圆的内接四边形;
顶点在圆上的四边形叫圆内接四边形,该圆叫四边形的外接圆。
5.圆的内接四边形的性质定理;
圆的内接四边形的对角互补。
https://www.21cnjy.com/help/help_extract.php
24.1.4
圆周角
人教版
九年级上册
.
O
A
问题:将圆心角顶点向上移,直至与⊙O相交于点C,观察得到的∠ACB。
C
顶点在圆上
两边都与圆相交
这样的角叫圆周角。
B
问:顶点在哪里?两边与圆有什么的位置关系?
探究
E
.
O
B
C
A
.
O
B
C
D
.
O
B
C
A
试一试
试着画一画,一条弧所对的圆周角有多少个?
一条弧所对的圆周角有无数个
虽然一条弧所对的圆周角有无数个,但观察它们与圆心的位置关系,可分成那几种情况?
(3)圆心在圆周角外
(1)圆心在圆周角的一边上
(2)圆心在圆周角内
如图,量一量每个图中圆周角∠BAC与圆心角∠BOC的度数,它们的大小有什么关系?
A
B
C
O
A
B
C
O
A
B
C
O
1.第一种情况:圆心在角的一边上
A
B
C
O
∵
OA=OC
∴∠A=∠OCA
又
∠BOC=∠A+∠OCA
∴∠BOC=2∠A
即∠A=
∠BOC
一条弧所对的圆周角等于这条弧所对的圆心角的度数的一半。
猜想并证明
A
B
C
O
D
2.第二种情况:圆心在角的内部
问:直径AD辅助线有什么作用?与第一个图案对比你有什么发现?
3.第三种情况:圆心在角的外部
A
B
C
O
D
你能看出图中有第一个图的基本模型吗?
证明∠BAC=
∠BOC
圆周角定理:
一条弧所对的圆周角等于它所对的圆心角的一半。
A
B
C
O
即∠BAC=
∠BOC
或∠BOC=
2
∠BAC
BC所对的圆周角
∠
BAC
,∠
BDC,∠
BEC,的大小有什么关系?为什么?
⌒
规律:都相等,都等于圆心角∠BOC的一半
圆周角推论:同弧或等弧所对的圆周角相等。
探究
E
D
.
O
B
C
A
推论1:同圆或等圆中,相等的圆周角所对的弧也相等。
D
A
B
O
C
E
F
F
∵
∠CAD=∠EBF
∴
CD=EF
)
)
推论2:半圆(或直径)所对的圆周角是直角,900的圆周角所对的弦是直径。
A
O
B
C1
C2
C3
∵
AB是直径
∴
∠AC1B=900
∵
∠AC1B=900
∴
AB是直径
新课讲解:
若一个多边形各顶点都在同一个圆上,那么,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆。
O
B
C
D
E
F
A
O
A
C
D
E
B
O
C
A
B
D
如图,
四边形ABCD为⊙O的内接四边形;
⊙O为四边形ABCD的外接圆。
思考:
∠A与∠C有什么关系?
∠B与∠D有什么关系?
C
O
D
B
A
如图:圆内接四边形ABCD中,
∵
弧BCD和弧BAD所对的圆心角的和是周角
∴∠A+∠C=
360°÷2=
180°
同理∠B+∠D=180°
结论:圆的内接四边形的对角互补。
符号表达式:
∵四边形ABCD是⊙O的内接四边形,
∴
∠A+∠C=180°
∠B+∠D=180°
O
C
A
B
D
圆的内接四边形的性质:
圆的内接四边形的对角互补。
3、圆周角定理的推论:
同圆或等圆中,同弧或等弧所对的圆周角相等;
用于找相等的角
一条弧所对的圆周角等于它所对的圆心角的一半。
2、圆周角定理:
1、圆周角定义:顶点在圆上,并且两边都和圆相交的角叫圆周角.
小结
小结
从特殊到一般的数学方法
转化思想(化归思想)
6、数学思想和方法:
分类讨论思想
4.圆的内接四边形;
顶点在圆上的四边形叫圆内接四边形,该圆叫四边形的外接圆。
5.圆的内接四边形的性质定理;
圆的内接四边形的对角互补。
https://www.21cnjy.com/help/help_extract.php
同课章节目录
