24.4.2 弧长和扇形面积 课件(共22张PPT)
文档属性
| 名称 | 24.4.2 弧长和扇形面积 课件(共22张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-04 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
24.4弧长和扇形面积
第2课时
人教版
九年级上册
1.了解圆锥母线的概念,理解圆锥侧面积计算公式,
理解圆锥全面积的计算方法,并会应用公式解决问题.
2.探索圆锥侧面积和全面积的计算公式并应用它解决
现实生活中的一些实际问题.
认识圆锥:生活中的圆锥
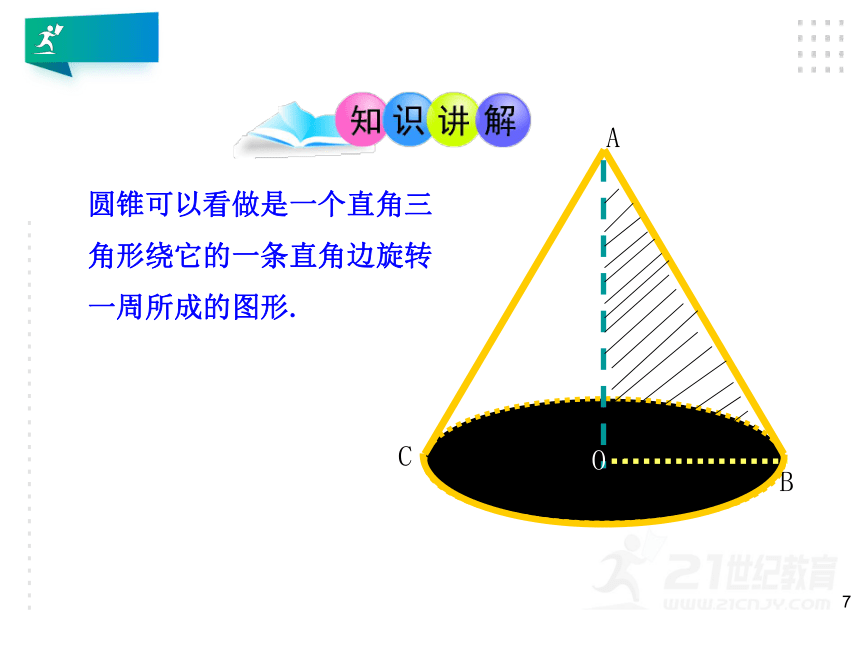
圆锥可以看做是一个直角三
角形绕它的一条直角边旋转
一周所成的图形.
O
A
B
C
A
A2
A1
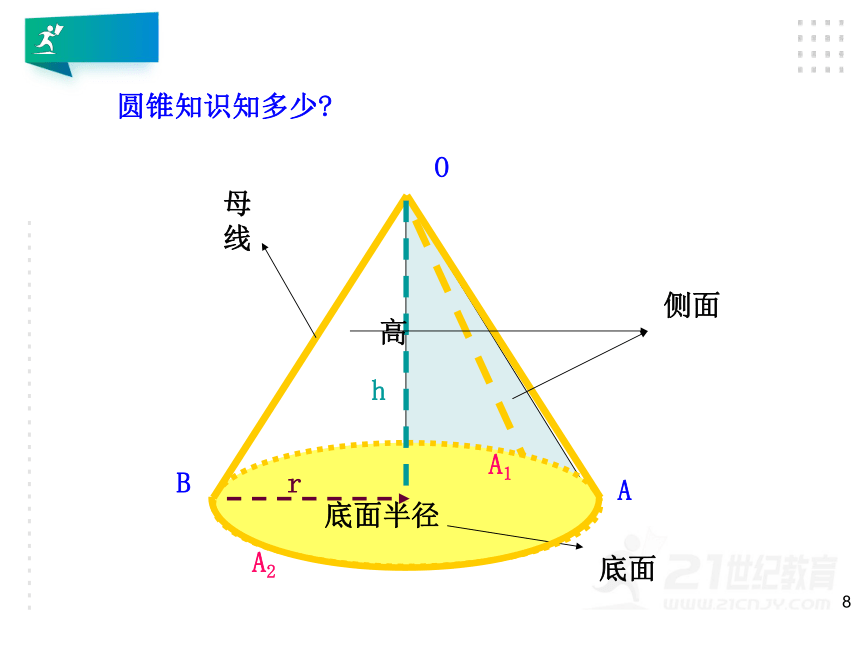
圆锥知识知多少?
h
r
母线
高
底面半径
底面
侧面
B
O
根据图形,圆锥的底面半径、母线及其高有什么数量关系?
B
A
O
设圆锥的底面半径为r,母线长为l,高为h,则有:
l
2=r2+h2.
即:OA2+OB2=AB2
如图,设圆锥的母线长为l,底面半径为r,
(1)此扇形的半径(R)是
,
(2)此扇形的弧长(L
)是
,
(3)此圆锥的侧面积(S侧)
是
;
(4)它的全面积(S全)是
.
圆锥的母线
是一个扇形.
圆锥底面的周长
圆锥的母线与扇形弧长积的一半
侧面展开图
圆锥的
是什么图形?
底面积与侧面积的和
圆锥的侧面积和全面积
O
┓
r
h
l
O
┓
r
h
l
θ
合作学习
弧长公式:c=
计算圆心角n的度数:
如何计算圆锥侧面展开图的圆心角θ的度数呢?
【例1】圆锥形烟囱帽(如图)的母线长为80cm,高为38.7cm,求
这个烟囱帽的面积.(
取3.14,结果保留2个有效数字)
【解析】∵l=80cm,h=38.7cm
∴r=
∴S侧=πrl≈3.14×70×80≈1.8×104
cm2
答:烟囱帽的面积约为1.8×104cm2.
例
题
填空:根据下列条件求值(其中r、h、l分别是圆锥的底面半径、高线、母线长)
(1)l
=2,r=1
则
h
=_______
(2)
h
=3,
r=4
则
l
=_______
(3)
l
=10,
h
=
8
则
r
=_______
跟踪训练
一个圆锥形的零件,
经过轴的剖面是一个等腰三角形,
这个三角形就叫做圆锥的轴截面;它的腰长等于圆锥的母线长,
底边长等于圆锥底面的直径.
圆锥的轴截面
A
B
C
O
如△ABC就是圆锥的轴截面
【例2】已知一个圆锥的轴截面△ABC是等边三角形,它的表面积为
,求这个圆锥的底面半径和母线的长.
【解析】∵圆锥轴截面△ABC是正三角形
∴l=2r
∴πr×2r+πr2=75π
∴r=5
cm,l=10
cm
答:圆锥的底面半径为5cm,母线长为10cm.
例
题
A
B
C
O
1.根据圆锥的下面条件,求它的侧面积和全面积:
(
1
)
r=12cm,
l=20cm
(
2
)
h=12cm,
r=5cm
2.一个圆锥的侧面展开图是半径为18cm,圆心角为240度的扇形.则这个圆锥的底面半径为_______.
12cm
跟踪训练
S侧=240π,
S全=384π
S侧=65π,
S全=90π
1.(晋江·中考)已知圆锥的高是30cm,母线长是50cm,则圆锥的侧面积是_______.
【解析】
答案:
【解析】
答案:
2.(眉山·中考)已知圆锥的底面半径为4cm,
高为3cm,则这个圆锥的侧面积为__________cm2.
4.扇形的半径为30,圆心角为120°用它做一个圆锥模型的侧面,求这个圆锥的底面半径和高.
r=10;h=
3.圆锥的底面直径为80cm.母线长为90cm,求它的全面积.
S全=5200
cm2
通过本课时的学习,需要我们:
1.了解圆锥母线的概念,理解圆锥侧面积计算公式.
2.理解圆锥全面积的计算方法,并会应用公式解决问题.
https://www.21cnjy.com/help/help_extract.php
24.4弧长和扇形面积
第2课时
人教版
九年级上册
1.了解圆锥母线的概念,理解圆锥侧面积计算公式,
理解圆锥全面积的计算方法,并会应用公式解决问题.
2.探索圆锥侧面积和全面积的计算公式并应用它解决
现实生活中的一些实际问题.
认识圆锥:生活中的圆锥
圆锥可以看做是一个直角三
角形绕它的一条直角边旋转
一周所成的图形.
O
A
B
C
A
A2
A1
圆锥知识知多少?
h
r
母线
高
底面半径
底面
侧面
B
O
根据图形,圆锥的底面半径、母线及其高有什么数量关系?
B
A
O
设圆锥的底面半径为r,母线长为l,高为h,则有:
l
2=r2+h2.
即:OA2+OB2=AB2
如图,设圆锥的母线长为l,底面半径为r,
(1)此扇形的半径(R)是
,
(2)此扇形的弧长(L
)是
,
(3)此圆锥的侧面积(S侧)
是
;
(4)它的全面积(S全)是
.
圆锥的母线
是一个扇形.
圆锥底面的周长
圆锥的母线与扇形弧长积的一半
侧面展开图
圆锥的
是什么图形?
底面积与侧面积的和
圆锥的侧面积和全面积
O
┓
r
h
l
O
┓
r
h
l
θ
合作学习
弧长公式:c=
计算圆心角n的度数:
如何计算圆锥侧面展开图的圆心角θ的度数呢?
【例1】圆锥形烟囱帽(如图)的母线长为80cm,高为38.7cm,求
这个烟囱帽的面积.(
取3.14,结果保留2个有效数字)
【解析】∵l=80cm,h=38.7cm
∴r=
∴S侧=πrl≈3.14×70×80≈1.8×104
cm2
答:烟囱帽的面积约为1.8×104cm2.
例
题
填空:根据下列条件求值(其中r、h、l分别是圆锥的底面半径、高线、母线长)
(1)l
=2,r=1
则
h
=_______
(2)
h
=3,
r=4
则
l
=_______
(3)
l
=10,
h
=
8
则
r
=_______
跟踪训练
一个圆锥形的零件,
经过轴的剖面是一个等腰三角形,
这个三角形就叫做圆锥的轴截面;它的腰长等于圆锥的母线长,
底边长等于圆锥底面的直径.
圆锥的轴截面
A
B
C
O
如△ABC就是圆锥的轴截面
【例2】已知一个圆锥的轴截面△ABC是等边三角形,它的表面积为
,求这个圆锥的底面半径和母线的长.
【解析】∵圆锥轴截面△ABC是正三角形
∴l=2r
∴πr×2r+πr2=75π
∴r=5
cm,l=10
cm
答:圆锥的底面半径为5cm,母线长为10cm.
例
题
A
B
C
O
1.根据圆锥的下面条件,求它的侧面积和全面积:
(
1
)
r=12cm,
l=20cm
(
2
)
h=12cm,
r=5cm
2.一个圆锥的侧面展开图是半径为18cm,圆心角为240度的扇形.则这个圆锥的底面半径为_______.
12cm
跟踪训练
S侧=240π,
S全=384π
S侧=65π,
S全=90π
1.(晋江·中考)已知圆锥的高是30cm,母线长是50cm,则圆锥的侧面积是_______.
【解析】
答案:
【解析】
答案:
2.(眉山·中考)已知圆锥的底面半径为4cm,
高为3cm,则这个圆锥的侧面积为__________cm2.
4.扇形的半径为30,圆心角为120°用它做一个圆锥模型的侧面,求这个圆锥的底面半径和高.
r=10;h=
3.圆锥的底面直径为80cm.母线长为90cm,求它的全面积.
S全=5200
cm2
通过本课时的学习,需要我们:
1.了解圆锥母线的概念,理解圆锥侧面积计算公式.
2.理解圆锥全面积的计算方法,并会应用公式解决问题.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
