24.2直角三角形的性质(1) 华东师大版数学九年级上册 课件(共18张ppt)
文档属性
| 名称 | 24.2直角三角形的性质(1) 华东师大版数学九年级上册 课件(共18张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-04 12:12:10 | ||
图片预览




文档简介
(共18张PPT)
24.2
直角三角形的性质(1)
直角三角形的两个锐角互余
定理1:
B
A
C
直角三角形两直角边的平方和等于斜边
的平方
定理2:
忆一忆:
B
A
C
在Rt△ABC中,?ACB=90°
CD是斜边AB上的中线
如图24.2.1
求证:
CD=
AB.
D
已知:
A
C
B
D
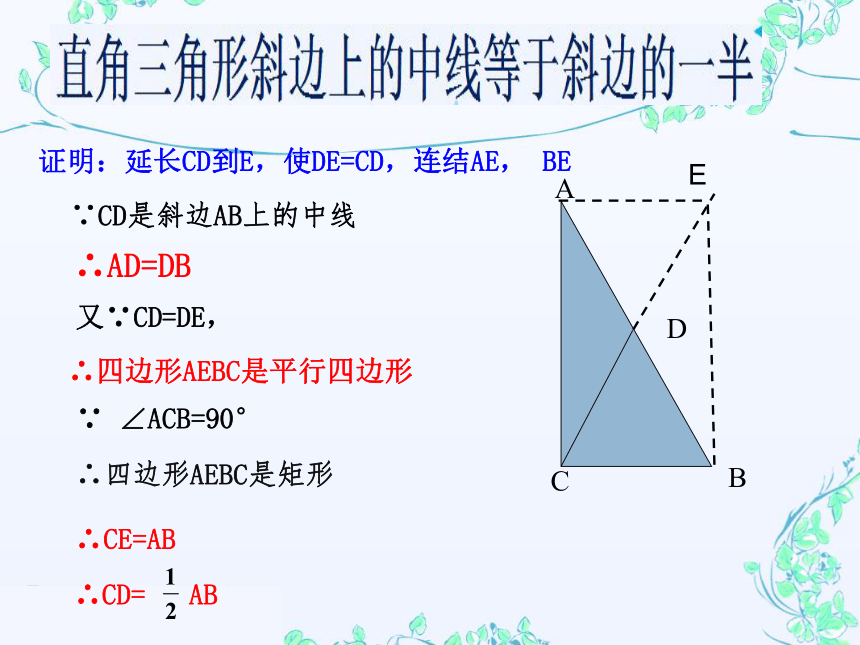
证明:延长CD到E,使DE=CD,连结AE,
BE
E
∵CD是斜边AB上的中线
∴AD=DB
又∵CD=DE,
∴四边形AEBC是平行四边形
∵
∠ACB=90°
∴四边形AEBC是矩形
∴CE=AB
∴CD=
AB
B
A
C
D
F
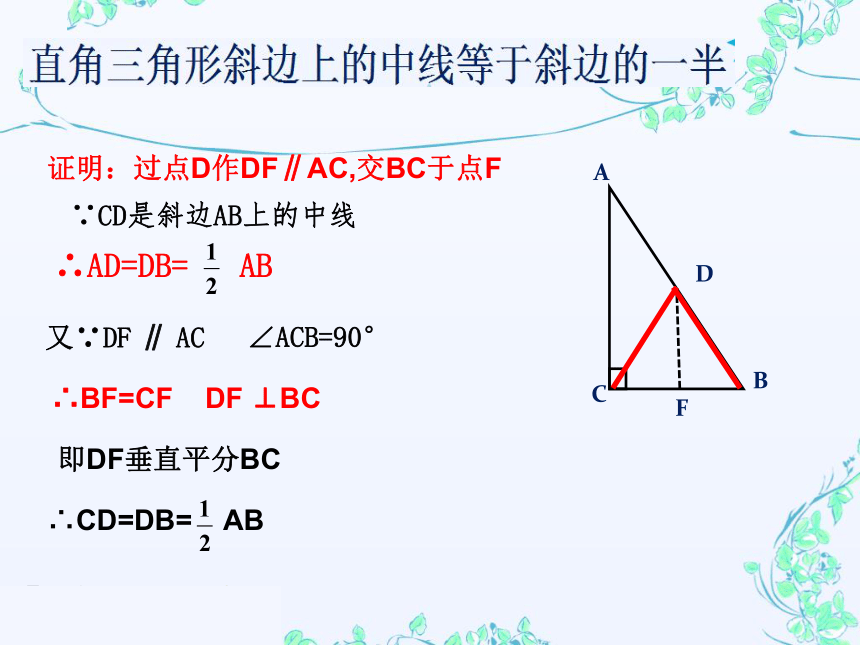
证明:过点D作DF∥AC,交BC于点F
∵CD是斜边AB上的中线
∴AD=DB=
AB
又∵DF
∥
AC
∠ACB=90°
∴BF=CF
DF
⊥BC
即DF垂直平分BC
∴CD=DB=
AB
定理3
B
A
C
D
E
B
A
C
D
F
直角三角形斜边上的中线等于斜边的一半
定理3
练习一:
1、判断下列说法是否正确:
(1)在△ACB中,CD是AB边上的中线,则CD=
AB.(
)
(2)在Rt△ACB中,∠ACB=90°,D是AB边上的一点,
则CD=
AB.(
)
(3)在Rt△ACB中,∠ACB=90°,AD是BC上的中线,则AD=
AB.(
)
B
A
C
D
直角
斜边
中线
×
×
×
直角三角形斜边上的中线等于斜边的一半
定理3
练习:
2、已知:在Rt△ABC中,∠ABC=90°,BM是AC边上的中线
(1)若BM=8,则AM=____,CM=____,AC=___;
(2)若∠C=25°,∠AMB=______°;
B
A
C
M
8
8
16
50
(3)若BD是AC边上的高,则与∠A相等的角有_____个.
直角三角形斜边上的中线等于斜边的一半
定理3
练习:
2、已知:在Rt△ABC中,∠ABC=90°,BM是AC边上的中线
B
A
C
M
(3)若BD是AC边上的高,则与∠A相等的角有_____个.
2
D
B
A
C
D
B
A
C
M
知道怎样剪了吗?
已知:如图,在△
ABC中,AD
⊥
BC,
E、F分别是AB、
AC的中点,且DE=DF
求证:AB=AC.
D
A
B
C
E
F
中点
证明:
∵
AD
⊥
BC,
E、F分别是AB、
AC的中点
(已知)
∴DE=
AB
DF=
AC
又∵DE=DF
(直角三角形斜边上的中线等于斜边的一半)
(已知)
∴AB=AC
(等量代换)
已知:如图,在△
ABC中,AD
⊥
BC,
E、F分别是AB、
AC的中点,且
求证:
D
A
B
C
E
F
DE=DF
AB=AC
DE=DF
AB=AC
如图1,在Rt
△
ABC与Rt
△
ACE中,
∠
ABC=
∠
AEC=90
°,点M是AC边上的中点,连结BM、EM、BE,点P是BE的中点.
求证:
E
A
B
C
M
P
证明:
(已知)
∵
∠
ABC=
∠
AEC=90
°
M是AC边上的中点
(已知)
(等量代换)
∴
BM=
AC
,EM=
AC
(直角三角形斜边上的中线等于斜边的一半)
∴
BM=
EM
又∵
P是BE边上的中点
∴
MP
⊥
BE
(等腰三角形三线合一)
(图1)
MP
⊥
BE
C
证明:
∵
∠
ABC=
∠
AEC=90
°
M是AC边上的中点
∴
BM=
AC
,BE=
AC
∴
BM=
EM
又∵
P是BE边上的中点
∴
MP
⊥BE
(已知)
(已知)
(等量代换)
(直角三角形斜边上的中线等于斜边的一半)
(等腰三角形三线合一)
如图2,在Rt
△
ABC与Rt
△
ACE中,
∠
ABC=
∠
AEC=90
°,点M是AC边上的中点,连结BM、EM、BE,点P是BE的中点.
求证:MP
⊥
BE
.
(图1)
E
A
C
M
P
(图1)
B
(图2)
M
E
D
A
C
M
P
如图3,在△ACD中,AE、CB分别是边CD、AD上的高,M、
P分别是AC、BE的中点.
求证:MP
⊥
BE
.
证明:
∵
∠AEC=
∠ABC=90
°
M是AC边上的中点
∴ME=
AC
,MB=
AC
∴
ME=
MB
又∵
P是BE边上的中点
∴
MP
⊥
BE
(图3)
(已知)
(已知)
(等量代换)
(直角三角形斜边上的中线等于斜边的一半)
(等腰三角形三线合一)
B
连结ME、MB
斜边相等的两个直角三角形,斜边上的中线也相等
B
A
C
M
B
A
C
M
1.直角三角形的两个锐角互余
3.直角三角形斜边上的中线等于斜边的一半
直角三角形的性质
2.直角三角形两直角边的平方和等于斜边的平方
证明一条线段是另一条线段的1/2或2倍,
(1)常用的定理:(2)添辅助线的方法:
已知:如图,在Rt△
ABC中,
∠
C=90
°
,
AD
∥
BC,
∠CBE=
∠ABE
.
求证:ED=2AB.
D
A
B
C
E
课外思考
挑战自我
“给我最大快乐的,不是已懂的知识,而是不断的学习;不是已有的东西,而是不断的获取;不是已达到的高度,而是继续不断的攀登”
---高斯
愿同学们:努力学习!勇攀高峰!
温馨寄语
24.2
直角三角形的性质(1)
直角三角形的两个锐角互余
定理1:
B
A
C
直角三角形两直角边的平方和等于斜边
的平方
定理2:
忆一忆:
B
A
C
在Rt△ABC中,?ACB=90°
CD是斜边AB上的中线
如图24.2.1
求证:
CD=
AB.
D
已知:
A
C
B
D
证明:延长CD到E,使DE=CD,连结AE,
BE
E
∵CD是斜边AB上的中线
∴AD=DB
又∵CD=DE,
∴四边形AEBC是平行四边形
∵
∠ACB=90°
∴四边形AEBC是矩形
∴CE=AB
∴CD=
AB
B
A
C
D
F
证明:过点D作DF∥AC,交BC于点F
∵CD是斜边AB上的中线
∴AD=DB=
AB
又∵DF
∥
AC
∠ACB=90°
∴BF=CF
DF
⊥BC
即DF垂直平分BC
∴CD=DB=
AB
定理3
B
A
C
D
E
B
A
C
D
F
直角三角形斜边上的中线等于斜边的一半
定理3
练习一:
1、判断下列说法是否正确:
(1)在△ACB中,CD是AB边上的中线,则CD=
AB.(
)
(2)在Rt△ACB中,∠ACB=90°,D是AB边上的一点,
则CD=
AB.(
)
(3)在Rt△ACB中,∠ACB=90°,AD是BC上的中线,则AD=
AB.(
)
B
A
C
D
直角
斜边
中线
×
×
×
直角三角形斜边上的中线等于斜边的一半
定理3
练习:
2、已知:在Rt△ABC中,∠ABC=90°,BM是AC边上的中线
(1)若BM=8,则AM=____,CM=____,AC=___;
(2)若∠C=25°,∠AMB=______°;
B
A
C
M
8
8
16
50
(3)若BD是AC边上的高,则与∠A相等的角有_____个.
直角三角形斜边上的中线等于斜边的一半
定理3
练习:
2、已知:在Rt△ABC中,∠ABC=90°,BM是AC边上的中线
B
A
C
M
(3)若BD是AC边上的高,则与∠A相等的角有_____个.
2
D
B
A
C
D
B
A
C
M
知道怎样剪了吗?
已知:如图,在△
ABC中,AD
⊥
BC,
E、F分别是AB、
AC的中点,且DE=DF
求证:AB=AC.
D
A
B
C
E
F
中点
证明:
∵
AD
⊥
BC,
E、F分别是AB、
AC的中点
(已知)
∴DE=
AB
DF=
AC
又∵DE=DF
(直角三角形斜边上的中线等于斜边的一半)
(已知)
∴AB=AC
(等量代换)
已知:如图,在△
ABC中,AD
⊥
BC,
E、F分别是AB、
AC的中点,且
求证:
D
A
B
C
E
F
DE=DF
AB=AC
DE=DF
AB=AC
如图1,在Rt
△
ABC与Rt
△
ACE中,
∠
ABC=
∠
AEC=90
°,点M是AC边上的中点,连结BM、EM、BE,点P是BE的中点.
求证:
E
A
B
C
M
P
证明:
(已知)
∵
∠
ABC=
∠
AEC=90
°
M是AC边上的中点
(已知)
(等量代换)
∴
BM=
AC
,EM=
AC
(直角三角形斜边上的中线等于斜边的一半)
∴
BM=
EM
又∵
P是BE边上的中点
∴
MP
⊥
BE
(等腰三角形三线合一)
(图1)
MP
⊥
BE
C
证明:
∵
∠
ABC=
∠
AEC=90
°
M是AC边上的中点
∴
BM=
AC
,BE=
AC
∴
BM=
EM
又∵
P是BE边上的中点
∴
MP
⊥BE
(已知)
(已知)
(等量代换)
(直角三角形斜边上的中线等于斜边的一半)
(等腰三角形三线合一)
如图2,在Rt
△
ABC与Rt
△
ACE中,
∠
ABC=
∠
AEC=90
°,点M是AC边上的中点,连结BM、EM、BE,点P是BE的中点.
求证:MP
⊥
BE
.
(图1)
E
A
C
M
P
(图1)
B
(图2)
M
E
D
A
C
M
P
如图3,在△ACD中,AE、CB分别是边CD、AD上的高,M、
P分别是AC、BE的中点.
求证:MP
⊥
BE
.
证明:
∵
∠AEC=
∠ABC=90
°
M是AC边上的中点
∴ME=
AC
,MB=
AC
∴
ME=
MB
又∵
P是BE边上的中点
∴
MP
⊥
BE
(图3)
(已知)
(已知)
(等量代换)
(直角三角形斜边上的中线等于斜边的一半)
(等腰三角形三线合一)
B
连结ME、MB
斜边相等的两个直角三角形,斜边上的中线也相等
B
A
C
M
B
A
C
M
1.直角三角形的两个锐角互余
3.直角三角形斜边上的中线等于斜边的一半
直角三角形的性质
2.直角三角形两直角边的平方和等于斜边的平方
证明一条线段是另一条线段的1/2或2倍,
(1)常用的定理:(2)添辅助线的方法:
已知:如图,在Rt△
ABC中,
∠
C=90
°
,
AD
∥
BC,
∠CBE=
∠ABE
.
求证:ED=2AB.
D
A
B
C
E
课外思考
挑战自我
“给我最大快乐的,不是已懂的知识,而是不断的学习;不是已有的东西,而是不断的获取;不是已达到的高度,而是继续不断的攀登”
---高斯
愿同学们:努力学习!勇攀高峰!
温馨寄语
