3.4 方差 课件 2021—2022学年苏科版数学九年级上册(16张)
文档属性
| 名称 | 3.4 方差 课件 2021—2022学年苏科版数学九年级上册(16张) |
|
|
| 格式 | ppt | ||
| 文件大小 | 535.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-02 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
问题引入
1、甲、乙两名同学本学期五次测验的数学成绩分别如下表(单位:分):
甲
85
90
90
90
95
乙
95
85
95
85
90
假如要竞赛,老师要从甲、乙两名同学中挑选一个参加,你认为挑哪一位较合适?
(1)分别计算两名同学的平均成绩;
?
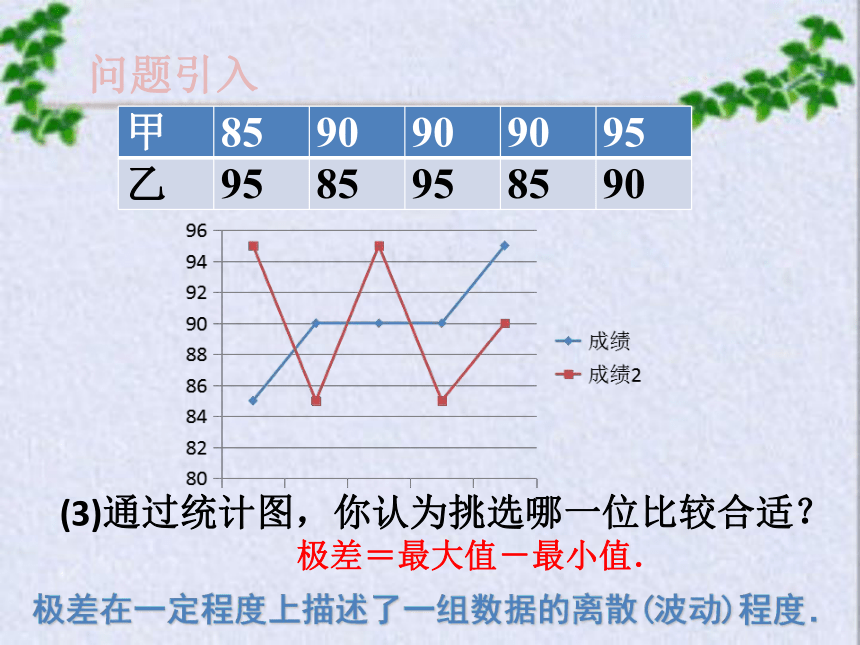
(2)根据这两名同学的成绩画出折线统计图.
甲
85
90
90
90
95
乙
95
85
95
85
90
问题引入
(3)通过统计图,你认为挑选哪一位比较合适?
甲
85
90
90
90
95
乙
95
85
95
85
90
问题引入
极差=最大值-最小值.
极差在一定程度上描述了一组数据的离散(波动)程度.
谁的稳定性好?应以什么数据来衡量呢?
①各数据与平均值偏差的和来衡量数据的稳定性?
甲:(85-90)+(90-90)+(90-90)+(90-90)+(95-90)=0
乙:(95-90)+(85-90)+(95-90)+(85-90)+(90-90)=0
②用偏差的平方和来衡量数据的稳定性?
甲:(85-90)2+(90-90)2+(90-90)2+(90-90)2+(95-90)2=50
乙:(
95-90)2+(85-90)2+(95-90)2+(85-90)2+(90-90)2=100
问题引入
③若甲有6次测验成绩,而乙只有5次测验成绩,分别如下(单位:分):
甲
85
90
90
95
95
85
乙
95
85
95
85
90
?
?
?
上述各偏差的平方和的大小还与什么有关?
与考试的次数有关
问题引入
?
所以要进一步用“各偏差的平均数”来衡量数据的稳定性.
问题引入
甲
85
90
90
95
95
85
乙
95
85
95
85
90
?
3.4方差
方差用来衡量一组数据的波动大小(即这组数据偏离平均数的大小),方差越大,说明数据离散程度越大,越不稳定.
来表示这组数据的离散程度,并把它们叫做这组数据
的方差.
在一组数据
x1
,x2
,…,xn
中,各数据与它们的
平均数的差的平方分别是
我们用它们的平均数,即
计算方差的步骤:“先平均,后求差,平方后,再平均”.
知识归纳
在有些情况下,需要用方差的算术平方根,即
?
来描述一组数据的离散程度,并把它叫做这组数据的标准差.
知识归纳
例1
计算下列两组数据的方差与标准差:
(1)
1,
2,
3,
4,
5;
(2)104,101,96,102,97。
学以致用
在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团都表演了舞剧《天鹅湖》,参加表演的女演员身高(单位:cm)如下表所示:
甲
163
164
164
165
165
166
166
167
乙
163
165
165
166
166
167
168
168
哪个芭蕾舞团女演员的身高更整齐?
学以致用
我们知道,一组数据的方差越小,这组数据就越稳定,那么,是不是方差越小就表示这组数据越好?
例2甲、乙两名队员参加射击训练,成绩分别
被制成下列两个统计图:
根据以上信息,整理分析数据如下:
(1)写出表格中a,b,c的值;
平均成绩/环
中位数/环
众数/环
方差
甲
a
7
7
1.2
乙
7
b
8
c
学以致用
平均成绩/环
中位数/环
众数/环
方差
甲
7
7
7
1.2
乙
7
7.5
8
4.2
根据以上信息:
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
学以致用
方差越小表示这组数据越稳定,但不是方差越小就表示这组数据越好,而是对具体的情况进行具体分析才能得出正确的结论。
1.平均数:反映数据的平均水平;
2.中位数:数据从小到大排列后,处于中间
位置的数或中间两数的平均数;
3.众
数:出现次数最多的数;
4.极
差:反映数据变化范围的大小,易受
极端值影响;
5.方
差:反映数据波动的大小;
6.标准差:反映数据波动的大小,且与数据
单位一致.
数据的分析指标
集中趋势
离散程度
问题引入
1、甲、乙两名同学本学期五次测验的数学成绩分别如下表(单位:分):
甲
85
90
90
90
95
乙
95
85
95
85
90
假如要竞赛,老师要从甲、乙两名同学中挑选一个参加,你认为挑哪一位较合适?
(1)分别计算两名同学的平均成绩;
?
(2)根据这两名同学的成绩画出折线统计图.
甲
85
90
90
90
95
乙
95
85
95
85
90
问题引入
(3)通过统计图,你认为挑选哪一位比较合适?
甲
85
90
90
90
95
乙
95
85
95
85
90
问题引入
极差=最大值-最小值.
极差在一定程度上描述了一组数据的离散(波动)程度.
谁的稳定性好?应以什么数据来衡量呢?
①各数据与平均值偏差的和来衡量数据的稳定性?
甲:(85-90)+(90-90)+(90-90)+(90-90)+(95-90)=0
乙:(95-90)+(85-90)+(95-90)+(85-90)+(90-90)=0
②用偏差的平方和来衡量数据的稳定性?
甲:(85-90)2+(90-90)2+(90-90)2+(90-90)2+(95-90)2=50
乙:(
95-90)2+(85-90)2+(95-90)2+(85-90)2+(90-90)2=100
问题引入
③若甲有6次测验成绩,而乙只有5次测验成绩,分别如下(单位:分):
甲
85
90
90
95
95
85
乙
95
85
95
85
90
?
?
?
上述各偏差的平方和的大小还与什么有关?
与考试的次数有关
问题引入
?
所以要进一步用“各偏差的平均数”来衡量数据的稳定性.
问题引入
甲
85
90
90
95
95
85
乙
95
85
95
85
90
?
3.4方差
方差用来衡量一组数据的波动大小(即这组数据偏离平均数的大小),方差越大,说明数据离散程度越大,越不稳定.
来表示这组数据的离散程度,并把它们叫做这组数据
的方差.
在一组数据
x1
,x2
,…,xn
中,各数据与它们的
平均数的差的平方分别是
我们用它们的平均数,即
计算方差的步骤:“先平均,后求差,平方后,再平均”.
知识归纳
在有些情况下,需要用方差的算术平方根,即
?
来描述一组数据的离散程度,并把它叫做这组数据的标准差.
知识归纳
例1
计算下列两组数据的方差与标准差:
(1)
1,
2,
3,
4,
5;
(2)104,101,96,102,97。
学以致用
在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团都表演了舞剧《天鹅湖》,参加表演的女演员身高(单位:cm)如下表所示:
甲
163
164
164
165
165
166
166
167
乙
163
165
165
166
166
167
168
168
哪个芭蕾舞团女演员的身高更整齐?
学以致用
我们知道,一组数据的方差越小,这组数据就越稳定,那么,是不是方差越小就表示这组数据越好?
例2甲、乙两名队员参加射击训练,成绩分别
被制成下列两个统计图:
根据以上信息,整理分析数据如下:
(1)写出表格中a,b,c的值;
平均成绩/环
中位数/环
众数/环
方差
甲
a
7
7
1.2
乙
7
b
8
c
学以致用
平均成绩/环
中位数/环
众数/环
方差
甲
7
7
7
1.2
乙
7
7.5
8
4.2
根据以上信息:
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
学以致用
方差越小表示这组数据越稳定,但不是方差越小就表示这组数据越好,而是对具体的情况进行具体分析才能得出正确的结论。
1.平均数:反映数据的平均水平;
2.中位数:数据从小到大排列后,处于中间
位置的数或中间两数的平均数;
3.众
数:出现次数最多的数;
4.极
差:反映数据变化范围的大小,易受
极端值影响;
5.方
差:反映数据波动的大小;
6.标准差:反映数据波动的大小,且与数据
单位一致.
数据的分析指标
集中趋势
离散程度
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
