平行线等分线段定理
图片预览

文档简介
1.1平行线等分线段定理
编制人: 审核人: 领导签字:
【学习目标】
1.了解平行线等分线段定理产生的背景,体验定理的产生过程。
2.探索并理解定理的证明过程。
3.掌握平行线等分线段定理及其推论,能应用其定理及推论解决有关几何计算问题和证明问题。
4.通过本节学习,体会从特殊到一般发现数学结论的思想方法。
【重点难点】
学习重点:平行线等分线段定理及其推论
教学难点:平行线等分线段定理及其推论的应用。
【自学导引】1.用30分钟的时间阅读课本P66-P71页的内容,完成课前预习内容。并将预习过程中的疑惑写在我的疑惑里。
2.小组合作完成探究一至二的任务,准备课堂随机展示,点评。
【课前预习】
一、问题导学
问题1:平行线等分线段定理:
如果一组平行线在一条直线上截得的线段 ,
那么在其他直线上截得的线段 。
问题2:平行线等分线段定理推论:
推论1:经过三角形一边的中点与另一边平行的直线必 。
推论2:经过梯形一腰的中点,且与底边平行的直线 。
问题3:三角形中位线定理:
三角形的中位线平行于 ,并且等于 。
二、预习自测
1.如图1-7 ,D,E分别是△ABC中AB边和AC边的中点。求证:DE∥BC且DE=1/2BC
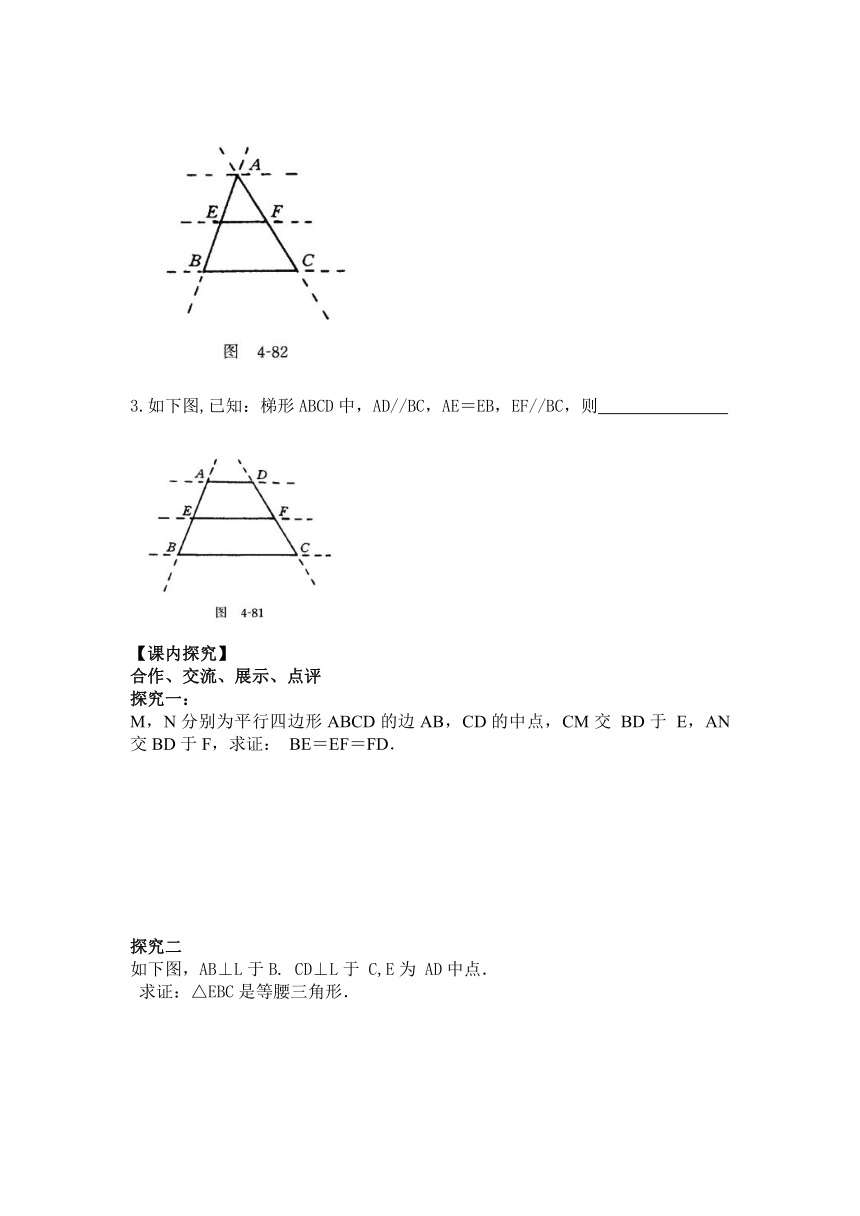
2.如下图,已知: △ABC中, AE=EB, EF//BC,则
3.如下图,已知:梯形ABCD中,AD//BC,AE=EB,EF//BC,则
【课内探究】
合作、交流、展示、点评
探究一:
M,N分别为平行四边形ABCD的边AB,CD的中点,CM交 BD于 E,AN交BD于F,求证: BE=EF=FD.
探究二
如下图,AB⊥L于B. CD⊥L于 C,E为 AD中点.
求证:△EBC是等腰三角形.
【学生疑惑】
【总结提升】
【当堂检测】
1. 如图EF∥BC,FD∥AB,AE=1.8cm,BE=1.2cm,CD=1.4cm.则BD= .
2. 顺次连结等腰梯形的两底中点和两条对角线的中点所组成的四边形一定是( )
A.菱形 B.矩形 C.正方形 D.梯形
3.已知:在□ABCD中,E、F分别为AD、BC的中点,连BE、DF交AC于G、H点.求证:AG=GH=HC
4.在△ABC中,M是AB的中点,MD//BC,证明AD=DC.
【作业布置】
1. 课本P47页1、2、3
2.导学方案上的题
【学习札记】
日期:2011-4-12 主编:高顺丽 审核:刘辉 课型:新授型 编号⒂ 班级_________姓名_________
--------------------------------------------------------装------------------------------------------------订----------------------------------------------------线-------------------------------------------
A
B
C
D
F
E
编制人: 审核人: 领导签字:
【学习目标】
1.了解平行线等分线段定理产生的背景,体验定理的产生过程。
2.探索并理解定理的证明过程。
3.掌握平行线等分线段定理及其推论,能应用其定理及推论解决有关几何计算问题和证明问题。
4.通过本节学习,体会从特殊到一般发现数学结论的思想方法。
【重点难点】
学习重点:平行线等分线段定理及其推论
教学难点:平行线等分线段定理及其推论的应用。
【自学导引】1.用30分钟的时间阅读课本P66-P71页的内容,完成课前预习内容。并将预习过程中的疑惑写在我的疑惑里。
2.小组合作完成探究一至二的任务,准备课堂随机展示,点评。
【课前预习】
一、问题导学
问题1:平行线等分线段定理:
如果一组平行线在一条直线上截得的线段 ,
那么在其他直线上截得的线段 。
问题2:平行线等分线段定理推论:
推论1:经过三角形一边的中点与另一边平行的直线必 。
推论2:经过梯形一腰的中点,且与底边平行的直线 。
问题3:三角形中位线定理:
三角形的中位线平行于 ,并且等于 。
二、预习自测
1.如图1-7 ,D,E分别是△ABC中AB边和AC边的中点。求证:DE∥BC且DE=1/2BC
2.如下图,已知: △ABC中, AE=EB, EF//BC,则
3.如下图,已知:梯形ABCD中,AD//BC,AE=EB,EF//BC,则
【课内探究】
合作、交流、展示、点评
探究一:
M,N分别为平行四边形ABCD的边AB,CD的中点,CM交 BD于 E,AN交BD于F,求证: BE=EF=FD.
探究二
如下图,AB⊥L于B. CD⊥L于 C,E为 AD中点.
求证:△EBC是等腰三角形.
【学生疑惑】
【总结提升】
【当堂检测】
1. 如图EF∥BC,FD∥AB,AE=1.8cm,BE=1.2cm,CD=1.4cm.则BD= .
2. 顺次连结等腰梯形的两底中点和两条对角线的中点所组成的四边形一定是( )
A.菱形 B.矩形 C.正方形 D.梯形
3.已知:在□ABCD中,E、F分别为AD、BC的中点,连BE、DF交AC于G、H点.求证:AG=GH=HC
4.在△ABC中,M是AB的中点,MD//BC,证明AD=DC.
【作业布置】
1. 课本P47页1、2、3
2.导学方案上的题
【学习札记】
日期:2011-4-12 主编:高顺丽 审核:刘辉 课型:新授型 编号⒂ 班级_________姓名_________
--------------------------------------------------------装------------------------------------------------订----------------------------------------------------线-------------------------------------------
A
B
C
D
F
E
