鲁教版(五四制)八上4.2.1图形的旋转 课件(15张)
文档属性
| 名称 | 鲁教版(五四制)八上4.2.1图形的旋转 课件(15张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-02 17:42:52 | ||
图片预览






文档简介
(共15张PPT)
1.通过观察具体实例理解旋转概念,能指出旋转中心、旋转方向、旋转角度。
2.探究旋转的性质,并在观察、猜想、验证、归纳、概括的探究过程中,发展合情推理能力,进一步体会图形运动中的变和不变.
学习重点:旋转的性质.
学习难点:旋转的性质.
一、认真阅读书P59练习以上部分
思考:
(1)说出什么是图形的旋转?
(2)在书中钟表上指出时针旋转的旋转中心
、旋转角、对应点。
这个定点O称为旋转中心,
点A与点B是一对对应点,
转动的角∠AOB称为旋转角.
旋转角
旋转中心
1、旋转:在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。
A
o
B
下列现象中属于旋转的有(
)个
①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.
A.2
B.3
C.4
D.5
C
B
O
A
45
0
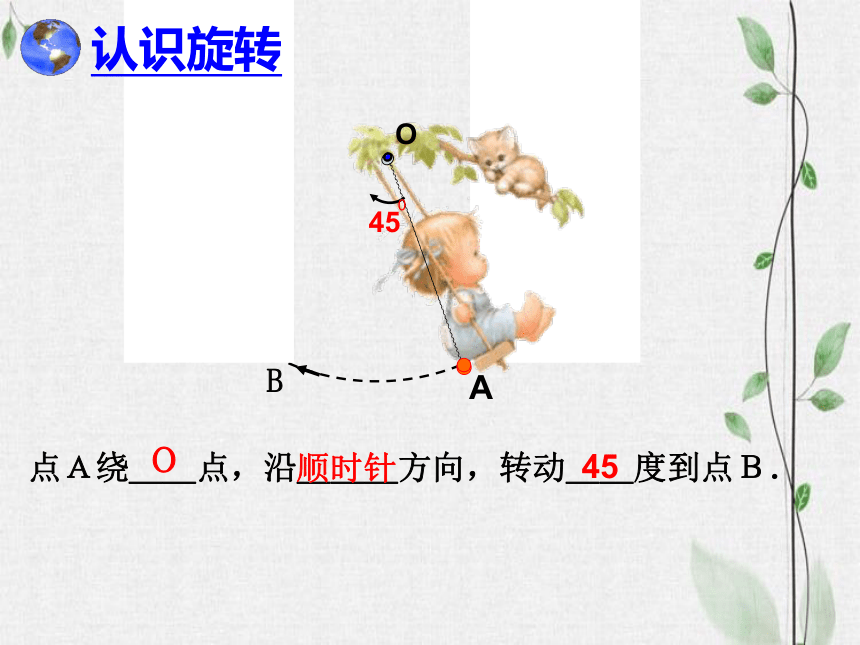
点A绕__点,沿___方向,转动__度到点B.
O
顺时针
45
认识旋转
认识旋转
P
B
A
B
/
A
/
90
0
线段AB绕__点,沿___方向,转动__度到线段A’B’.
P
逆时针
90
B
A
认识旋转
B?
A?
C
C?
O
100
0
旋转中心
旋转角度
旋转方向
旋转的三要素:
△ABC绕__点,沿___方向,转动__度到△A’B’C’
.
O
顺时针
100
如图,如果把钟表的指针看做四边形AOBC,它绕O点旋转得
到四边形DOEF.
在这个旋转过程中:
(1)旋转中心是什么?
(2)经过旋转,点A、B分别移动到什么位置?
(3)旋转角是什么?
(4)AO与DO的长有什么关系?BO与EO呢?
(5)∠AOD与∠BOE有什么大小关系?
旋转中心是O
点D和点E的位置
AO=DO,BO=EO
∠AOD=∠BOE
∠AOD和∠BOE都是旋转角
探究旋转性质
4、旋转前、后两图形全等.
1、对应点到旋转中心的距离相等.
每一对应点与旋转中心所连线段的夹角等于旋转角.
旋转的基本性质
2、对应角相等.
3、对应线段相等.
2、如图E是正方形ABCD内一点,将△ABE绕点B顺时针方向旋转到△CBF,其中EB=3cm,则BF=_____cm
,∠EBF=____,_
(1)△EBF是什么形状,为什么?
(2)EF等于多少?
3
90
练习3:
B
A
E
D
C
F
在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。
旋转的概念:
旋转的性质:
每一对应点与旋转中心所连线段的夹角等于旋转角.
1、对应点到旋转中心的距离相等
小结:
旋转三要素:旋转中心、旋转方向、旋转的角度。
2、对应角相等.
3、对应线段相等.
4、旋转前、后两图形全等.
布置作业:
有效课堂:P37、38。
1.通过观察具体实例理解旋转概念,能指出旋转中心、旋转方向、旋转角度。
2.探究旋转的性质,并在观察、猜想、验证、归纳、概括的探究过程中,发展合情推理能力,进一步体会图形运动中的变和不变.
学习重点:旋转的性质.
学习难点:旋转的性质.
一、认真阅读书P59练习以上部分
思考:
(1)说出什么是图形的旋转?
(2)在书中钟表上指出时针旋转的旋转中心
、旋转角、对应点。
这个定点O称为旋转中心,
点A与点B是一对对应点,
转动的角∠AOB称为旋转角.
旋转角
旋转中心
1、旋转:在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。
A
o
B
下列现象中属于旋转的有(
)个
①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.
A.2
B.3
C.4
D.5
C
B
O
A
45
0
点A绕__点,沿___方向,转动__度到点B.
O
顺时针
45
认识旋转
认识旋转
P
B
A
B
/
A
/
90
0
线段AB绕__点,沿___方向,转动__度到线段A’B’.
P
逆时针
90
B
A
认识旋转
B?
A?
C
C?
O
100
0
旋转中心
旋转角度
旋转方向
旋转的三要素:
△ABC绕__点,沿___方向,转动__度到△A’B’C’
.
O
顺时针
100
如图,如果把钟表的指针看做四边形AOBC,它绕O点旋转得
到四边形DOEF.
在这个旋转过程中:
(1)旋转中心是什么?
(2)经过旋转,点A、B分别移动到什么位置?
(3)旋转角是什么?
(4)AO与DO的长有什么关系?BO与EO呢?
(5)∠AOD与∠BOE有什么大小关系?
旋转中心是O
点D和点E的位置
AO=DO,BO=EO
∠AOD=∠BOE
∠AOD和∠BOE都是旋转角
探究旋转性质
4、旋转前、后两图形全等.
1、对应点到旋转中心的距离相等.
每一对应点与旋转中心所连线段的夹角等于旋转角.
旋转的基本性质
2、对应角相等.
3、对应线段相等.
2、如图E是正方形ABCD内一点,将△ABE绕点B顺时针方向旋转到△CBF,其中EB=3cm,则BF=_____cm
,∠EBF=____,_
(1)△EBF是什么形状,为什么?
(2)EF等于多少?
3
90
练习3:
B
A
E
D
C
F
在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。
旋转的概念:
旋转的性质:
每一对应点与旋转中心所连线段的夹角等于旋转角.
1、对应点到旋转中心的距离相等
小结:
旋转三要素:旋转中心、旋转方向、旋转的角度。
2、对应角相等.
3、对应线段相等.
4、旋转前、后两图形全等.
布置作业:
有效课堂:P37、38。
