鲁教版(五四制)八上4.2.1图形的旋转 课件(17张)
文档属性
| 名称 | 鲁教版(五四制)八上4.2.1图形的旋转 课件(17张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-02 00:00:00 | ||
图片预览



文档简介
(共17张PPT)
平移的定义:
在平面内,将一个图形沿某个方向移动一定的距离,图形的这种变化称为平移。
经过平移,对应点连线平行(或共线)且相等
对应线段平行(或共线)且相等
对应角相等。
平移的性质:
温故而知新:
转动的车轮
转动的时针
荡秋千
这些情境,有什么共同的特征?
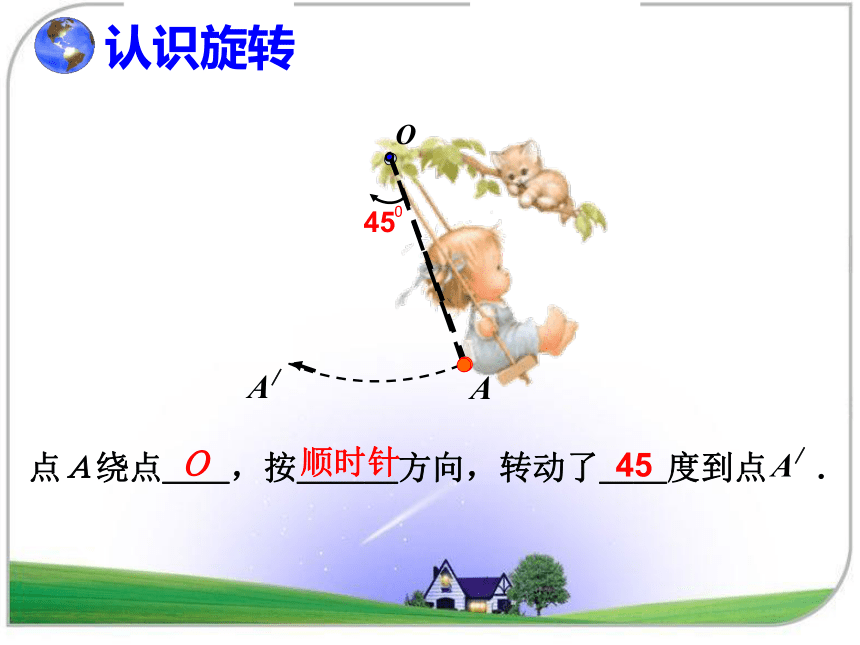
O
A
45
0
O
顺时针
45
认识旋转
A
/
点A绕点__,按___方向,转动了__度到点
.
A
/
P
B
A
B
/
A
/
90
0
线段AB绕点P,按逆时针方向,转动了90度到线段A'B'.
B
A
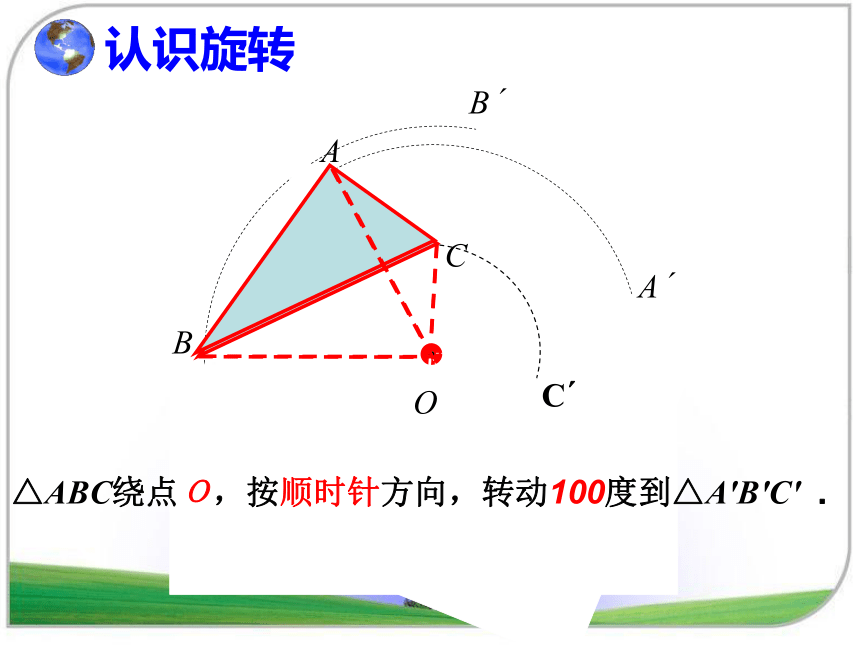
认识旋转
B?
A?
C
C?
O
△ABC绕点O,按顺时针方向,转动100度到△A'B'C'
.
旋转的定义
在平面内,将一个图形沿某个方向移动一定的距离,图形的这种变化称为平移。
在平面内,将一个图形绕一个定点按某个方向转动一个角度,图形的这种变化称为旋转。
平移:
旋转:
类比
(1)指出它的旋转中心和旋转角
(2)经过旋转,点A、B、C分别到达什么位置?
O
O
认识旋转
95
0
经过旋转图形上的每个点都绕同一点按相同方向转动相同的角度。
1.
下面生活中的实例,不是旋转的是(
)
A.
传送带传送货物
B.
螺旋桨的运动
C.
风车风轮的运动
D.
自行车车轮的运动
2.如图,
绕点O旋转45°后得到
,则点B的对应点是___;线段OB的对应线段是____;线段AB的对应线段是___;∠A的对应角是_____;∠B的对应角是_____;旋转中心是___;旋转角是____
__
A
D
OD
CD
O
探究旋转
探究旋转
旋转的性质
对应点到旋转中心的距离相等。
任意一组对应点与旋转中心的连线所成的角都等于旋转角。
对应线段相等,对应角相等。
应用旋转
(1)旋转中心是哪一点?
(2)旋转角是多少度?
1、如图,在正方形ABCD中,E是CB延长线上一点,△ABE经过旋转后得到△ADF,请按图回答:
A
B
F
C
E
G
D
H
(3)∠EAF等于多少度?
(4)经过旋转,点B与点E分别转到
什么位置?
(5)若点G是线段BE的中点,经过旋转
后,点G转到了什么位置?请在图形
上作出.
点A
900
900
点D、点F
应用旋转
回味旋转
我学到的知识:_________________.
我领悟的方法:
________________
.
我掌握的技能:
_________________.
我继续探究的:
_________________.
旋转的定义和性质
类比、特殊---一般
简单的旋转作图
如图,P是等边三角形ABC内一点,将ΔABP绕点B按顺时针方向旋转到ΔCBP'
的位置,PB=1。求PP'
的长.
快乐达标
平移的定义:
在平面内,将一个图形沿某个方向移动一定的距离,图形的这种变化称为平移。
经过平移,对应点连线平行(或共线)且相等
对应线段平行(或共线)且相等
对应角相等。
平移的性质:
温故而知新:
转动的车轮
转动的时针
荡秋千
这些情境,有什么共同的特征?
O
A
45
0
O
顺时针
45
认识旋转
A
/
点A绕点__,按___方向,转动了__度到点
.
A
/
P
B
A
B
/
A
/
90
0
线段AB绕点P,按逆时针方向,转动了90度到线段A'B'.
B
A
认识旋转
B?
A?
C
C?
O
△ABC绕点O,按顺时针方向,转动100度到△A'B'C'
.
旋转的定义
在平面内,将一个图形沿某个方向移动一定的距离,图形的这种变化称为平移。
在平面内,将一个图形绕一个定点按某个方向转动一个角度,图形的这种变化称为旋转。
平移:
旋转:
类比
(1)指出它的旋转中心和旋转角
(2)经过旋转,点A、B、C分别到达什么位置?
O
O
认识旋转
95
0
经过旋转图形上的每个点都绕同一点按相同方向转动相同的角度。
1.
下面生活中的实例,不是旋转的是(
)
A.
传送带传送货物
B.
螺旋桨的运动
C.
风车风轮的运动
D.
自行车车轮的运动
2.如图,
绕点O旋转45°后得到
,则点B的对应点是___;线段OB的对应线段是____;线段AB的对应线段是___;∠A的对应角是_____;∠B的对应角是_____;旋转中心是___;旋转角是____
__
A
D
OD
CD
O
探究旋转
探究旋转
旋转的性质
对应点到旋转中心的距离相等。
任意一组对应点与旋转中心的连线所成的角都等于旋转角。
对应线段相等,对应角相等。
应用旋转
(1)旋转中心是哪一点?
(2)旋转角是多少度?
1、如图,在正方形ABCD中,E是CB延长线上一点,△ABE经过旋转后得到△ADF,请按图回答:
A
B
F
C
E
G
D
H
(3)∠EAF等于多少度?
(4)经过旋转,点B与点E分别转到
什么位置?
(5)若点G是线段BE的中点,经过旋转
后,点G转到了什么位置?请在图形
上作出.
点A
900
900
点D、点F
应用旋转
回味旋转
我学到的知识:_________________.
我领悟的方法:
________________
.
我掌握的技能:
_________________.
我继续探究的:
_________________.
旋转的定义和性质
类比、特殊---一般
简单的旋转作图
如图,P是等边三角形ABC内一点,将ΔABP绕点B按顺时针方向旋转到ΔCBP'
的位置,PB=1。求PP'
的长.
快乐达标
