鲁教版(五四制)八上4.2.3旋转的应用—半角模型 课件(10张)
文档属性
| 名称 | 鲁教版(五四制)八上4.2.3旋转的应用—半角模型 课件(10张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 883.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-02 17:42:52 | ||
图片预览


文档简介
(共10张PPT)
旋
转
的
应
半角模型
用
认识半角模型,能在复杂的图形当中
找到半角模型;
会利用旋转的知识解决半角模型的相
关问题。
1
2
学习目标
知识回顾
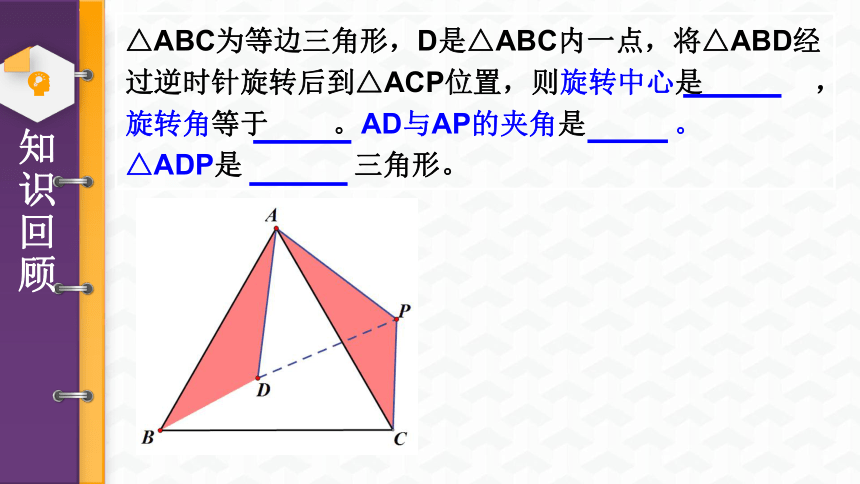
△ABC为等边三角形,D是△ABC内一点,将△ABD经过逆时针旋转后到△ACP位置,则旋转中心是
,旋转角等于
。AD与AP的夹角是
。
△ADP是
三角形。
典例探究
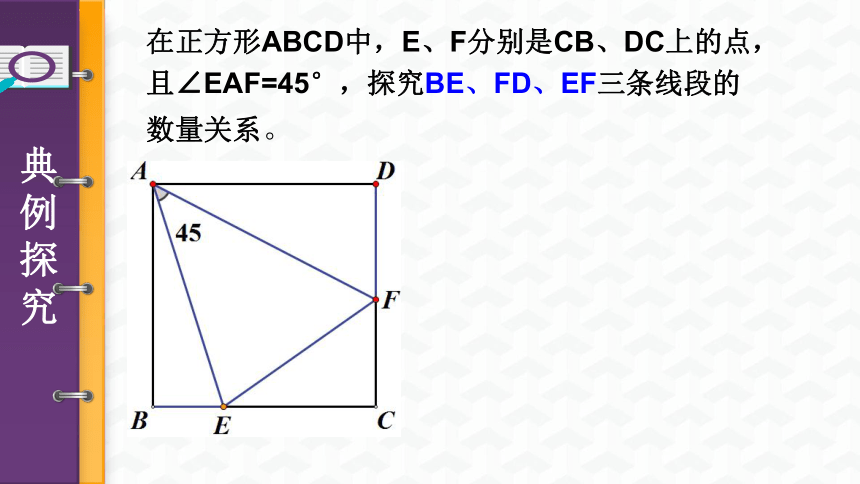
在正方形ABCD中,E、F分别是CB、DC上的点,且∠EAF=45°,探究BE、FD、EF三条线段的数量关系。
变式探究
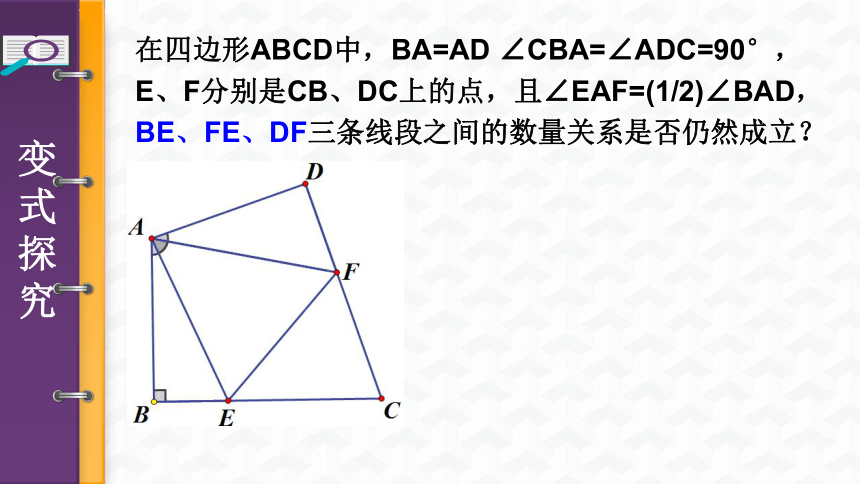
在四边形ABCD中,BA=AD
∠CBA=∠ADC=90°,
E、F分别是CB、DC上的点,且∠EAF=(1/2)∠BAD,
BE、FE、DF三条线段之间的数量关系是否仍然成立?
总结提炼
以公共端点为旋转中心,
相等的两条线段的夹角为旋转角.
等线段
倍半角
将分散的条件集中,隐藏的关系显现.
具有公共端点的等线段.
拓展延伸
等腰
Rt△ABC中,∠DAE=45°,
问BD、DE、EC三条线段之间的关系。
学以致用
在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏西70°的B处,两舰艇到指挥中心距离相等,接到指令后,舰艇甲向正东方向以60节的速度前进,舰艇乙沿北偏东50°方向以80节的速度前进,1.5小时后分别到达E、F处,两舰艇的夹角为70°,求E、F间的距离。
总结提升
通过本节课的学习,你有哪些收获?
先有直觉感知,
后有逻辑推理。
直觉指明方向,
逻辑完善过程。
课后拓展
正方形ABCD中,E、F分别是CB、CD延长线上的点,且∠EAF=45°,探索线段BE、DF与EF的数量关系。
旋
转
的
应
半角模型
用
认识半角模型,能在复杂的图形当中
找到半角模型;
会利用旋转的知识解决半角模型的相
关问题。
1
2
学习目标
知识回顾
△ABC为等边三角形,D是△ABC内一点,将△ABD经过逆时针旋转后到△ACP位置,则旋转中心是
,旋转角等于
。AD与AP的夹角是
。
△ADP是
三角形。
典例探究
在正方形ABCD中,E、F分别是CB、DC上的点,且∠EAF=45°,探究BE、FD、EF三条线段的数量关系。
变式探究
在四边形ABCD中,BA=AD
∠CBA=∠ADC=90°,
E、F分别是CB、DC上的点,且∠EAF=(1/2)∠BAD,
BE、FE、DF三条线段之间的数量关系是否仍然成立?
总结提炼
以公共端点为旋转中心,
相等的两条线段的夹角为旋转角.
等线段
倍半角
将分散的条件集中,隐藏的关系显现.
具有公共端点的等线段.
拓展延伸
等腰
Rt△ABC中,∠DAE=45°,
问BD、DE、EC三条线段之间的关系。
学以致用
在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏西70°的B处,两舰艇到指挥中心距离相等,接到指令后,舰艇甲向正东方向以60节的速度前进,舰艇乙沿北偏东50°方向以80节的速度前进,1.5小时后分别到达E、F处,两舰艇的夹角为70°,求E、F间的距离。
总结提升
通过本节课的学习,你有哪些收获?
先有直觉感知,
后有逻辑推理。
直觉指明方向,
逻辑完善过程。
课后拓展
正方形ABCD中,E、F分别是CB、CD延长线上的点,且∠EAF=45°,探索线段BE、DF与EF的数量关系。
