鲁教版(五四制)八上4.3.1 中心对称 课件(35张)
文档属性
| 名称 | 鲁教版(五四制)八上4.3.1 中心对称 课件(35张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-02 00:00:00 | ||
图片预览







文档简介
(共35张PPT)
课前活动
1.沿对角线对折,之后
再对折,展开
2.用剪刀按折痕(也就是两条对角线)剪开,但是,千万不要全剪开,而是剪到图中圆点所示位置.
3.将剪开的四个角按图中箭头方向分别折向纸的中心点,用胶棒固定住。
4.将粘好的雏形用一个大头钉固定好,这样,一架风车就做好啦
基于对学生思维训练的考虑和数学方法运用的引导以及揭示中心对称的性质,我又设计了如下问题,让每小组通过猜想找到规律,在实际量一量,动手折一折,最终得出结论。
猜一猜、量一量、折一折:做纸风车
猜一猜:你发现的规律是:____________;
量一量:用刻度尺和量角器量一下两个颜色一样的三角形各线段的长度和各个角的度数;
折一折:把其中两个颜色一样的三角形对折一下再次验证猜想得到的结论;
议一议:把结论归纳以下:______________。
试一试:你还能用什么方法说明这个结论?
看一看:通过看计算机的动画演示巩固得到的结论,形成表象。
what
way
who
why
自主探索,形成概念
问题
1:观察图形,是由哪些基本图形组成?
问题2:通过怎样变化可以将一个图形变换得到另一个图形??
问题
3:这些图形有什么共同特征?你还能举出一些类似的图形吗?
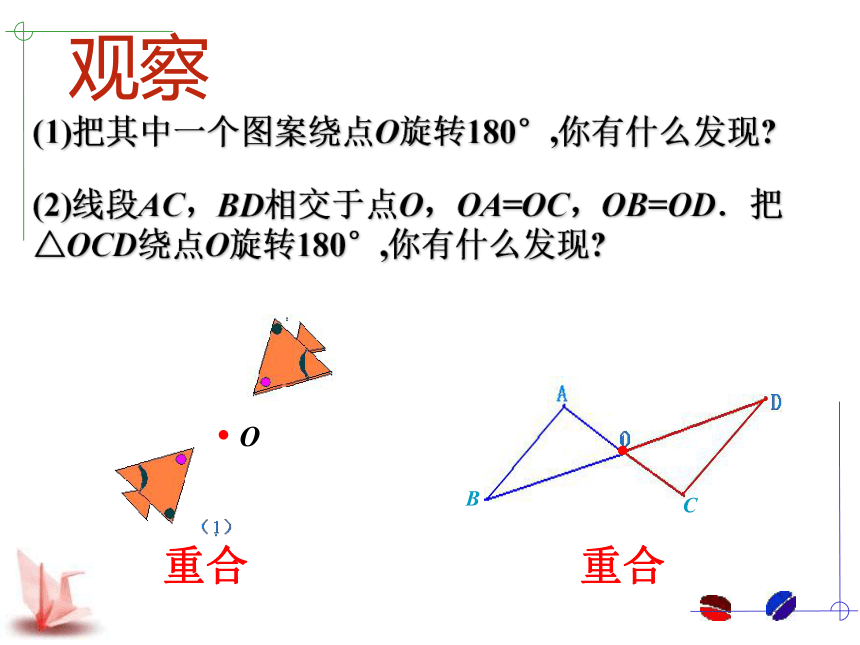
(1)把其中一个图案绕点O旋转180°,你有什么发现?
(2)线段AC,BD相交于点O,OA=OC,OB=OD.把
△OCD绕点O旋转180°,你有什么发现?
O
C
B
重合
重合
观察
在平面内,如果把一个图形绕着某个点旋转180°后,能与另一个图形重合,那么,就说这两个图形关于这个点成中心对称,这个点叫做对称中心。
两个图形上,经过旋转180°后重合的两个点叫做对应点。
形成概念:
A
B
C
A’
C’
B’
O
合作交流,探索性质
探究发现
旋转三角板,画关于点O对称的两个三角形:
画出的△ABC与△A′B′C′
关于点O对称.分别连接对称点
AA′、BB′、CC′。点O
在线段AA′上吗?如果在,
在什么位置?
△ABC与△A′B′C′有什么关系?
(1)点O是线段AA的中点
(2)△ABC≌△A′B′C′
第一步,画出△ABC;
第二步,以三角板的一个顶点O为中心,把三角板旋
转180°,画出△A′B′C′;
第三步,移开三角板.
A
B
C
A′
B′
C′
O
下图中△
A'
B'
C'
与△ABC关于点O成中心对称,你能从图中找到哪些等量关系?
(1)
OA=OA′、OB=OB′、
OC=OC′
(2)△ABC≌△A′B′C′
A
B
C
O
180°
A'
B'
c'
(1)关于中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心平分.
(2)关于中心对称的两个图形是全等形;
归纳性质:
∵
△
A'
B'
C'
与△ABC关于点O中心对称
∴
,
,
,
如图,已知△ABC与△A’B’C’中心对称,求出它们的对称中心O。
A
B
C
A’
B’
C’
解法一:根据观察,B、B’应是对应点,连结BB’,用刻度尺找出BB’的中点O,则点O即为所求(如图)
A
B
C
A’
B’
C’
O
O
解法二:根据观察,B、B’及C、C’应是两组对应点,连结BB’、CC’,BB’、CC’相交于点O,则点O即为所求(如图)。
A
B
C
A’
B’
C’
动手设计,迁移应用
A
O
A′
初级:点的中心对应点的作法
点A′即为所求的点
已知A点和O点,画出点A关于点O的对应点A'
A
A′
B′
B
O
中级:线段的中心对称线段的作法
已知线段AB和O点,画出线段AB关于点O
的对
称线段A'B'
线段A′
B′为所求作的线段
如图,选择点O为对称中心,画出与
△ABC关于点O对称的△A′B′C′.
A’
C’
B’
△A′B′C′即为所求的三角形.
1.
连接AO并延长到A′,使
OA
′=OA,得到点A的对称点A′.
2.
同样画B、C的对称点
B′、C′.
3.
顺次连接A′、B′、C′各点.
画法:
分析:确定一个三角形需要几个点?作一个三角形关于某点成中心对称的三角形,需要作几个点的对称点呢?
高级
已知四边形ABCD和O点,画出四边形ABCD
关于O点的对称图形。
.
C?
D?
A
B
D
C
O
A?
B?
画法:
1、连结AO
并延长到A?,使OA=OA?,得到点A的对称点A?
.
2、同样画B、C、D的对称点B?、C?、D?
3、顺次连结A?、B?、C?、D?各点
所以,四边形A?B?C?D?就是所求的四边形
画一个与已知四边形ABCD中心对称图形。
(1)以顶点A为对称中心;
(2)以BC边的中点O为对称中心。
D
A
B
C
E
F
G
M
D
A
B
C
O
.
N
先画出图形中的几个关键点(线段的端点、如多边形的顶点、圆的圆心等)关于某点的对称点,然后再顺次连结有关对称点即可。
(1)画一个点关于某点(对称中心)的对称点的画
法是:
先连接这个点与对称中心并延长一倍即可。
(2)画一个图形关于某点的对称图形的画法是:
2、如图,AO=DO,画出这个图形关于点O成中心对称的图形。
技师
3、如图,A、B两点的坐标分别是(3,2),(-4,1),
画出线段AB和它关于坐标原点成中心对称的线段A'B'。
高级技师:
A′
B′
C
′
O
A
B
C
如图,已知等边△ABC和点O,画△
A'
B'
C‘
使△A′B′C′和△ABC关于点O成中心对称.
移动一块正方形
(1)使得到图形只是轴对称图形;
(2)使得到图形只是中心对称图形;
(3)既是轴对称图形又是中心对称图形.
你最棒!
怎样判别两个图形关于某一点成中心对称呢?
如果两个图形的
对应点连成的线
段都经过某一点,
并且被该点平分,
那么这两个图形
一定关于这一点
成中心对称。
这节课你的收获是
你的疑惑
通过本节课的学习你有没有新的想法或发现?你觉得还有什么问题需要继续讨论吗?
讨论:中心对称与轴对称的区别:
轴对称
中心对称
有一条对称轴——直线
图形沿对称轴对折(翻折180°)后重合
折叠后与另一图形重合
对称点的连线被对称轴垂直平分
有一个对称中心——点
图形绕对称中心旋转180°后重合
旋转后与另一图形重合
对称点连线经过对称中心,
且被对称中心平分
课后延伸,实践应用
再见!
课前活动
1.沿对角线对折,之后
再对折,展开
2.用剪刀按折痕(也就是两条对角线)剪开,但是,千万不要全剪开,而是剪到图中圆点所示位置.
3.将剪开的四个角按图中箭头方向分别折向纸的中心点,用胶棒固定住。
4.将粘好的雏形用一个大头钉固定好,这样,一架风车就做好啦
基于对学生思维训练的考虑和数学方法运用的引导以及揭示中心对称的性质,我又设计了如下问题,让每小组通过猜想找到规律,在实际量一量,动手折一折,最终得出结论。
猜一猜、量一量、折一折:做纸风车
猜一猜:你发现的规律是:____________;
量一量:用刻度尺和量角器量一下两个颜色一样的三角形各线段的长度和各个角的度数;
折一折:把其中两个颜色一样的三角形对折一下再次验证猜想得到的结论;
议一议:把结论归纳以下:______________。
试一试:你还能用什么方法说明这个结论?
看一看:通过看计算机的动画演示巩固得到的结论,形成表象。
what
way
who
why
自主探索,形成概念
问题
1:观察图形,是由哪些基本图形组成?
问题2:通过怎样变化可以将一个图形变换得到另一个图形??
问题
3:这些图形有什么共同特征?你还能举出一些类似的图形吗?
(1)把其中一个图案绕点O旋转180°,你有什么发现?
(2)线段AC,BD相交于点O,OA=OC,OB=OD.把
△OCD绕点O旋转180°,你有什么发现?
O
C
B
重合
重合
观察
在平面内,如果把一个图形绕着某个点旋转180°后,能与另一个图形重合,那么,就说这两个图形关于这个点成中心对称,这个点叫做对称中心。
两个图形上,经过旋转180°后重合的两个点叫做对应点。
形成概念:
A
B
C
A’
C’
B’
O
合作交流,探索性质
探究发现
旋转三角板,画关于点O对称的两个三角形:
画出的△ABC与△A′B′C′
关于点O对称.分别连接对称点
AA′、BB′、CC′。点O
在线段AA′上吗?如果在,
在什么位置?
△ABC与△A′B′C′有什么关系?
(1)点O是线段AA的中点
(2)△ABC≌△A′B′C′
第一步,画出△ABC;
第二步,以三角板的一个顶点O为中心,把三角板旋
转180°,画出△A′B′C′;
第三步,移开三角板.
A
B
C
A′
B′
C′
O
下图中△
A'
B'
C'
与△ABC关于点O成中心对称,你能从图中找到哪些等量关系?
(1)
OA=OA′、OB=OB′、
OC=OC′
(2)△ABC≌△A′B′C′
A
B
C
O
180°
A'
B'
c'
(1)关于中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心平分.
(2)关于中心对称的两个图形是全等形;
归纳性质:
∵
△
A'
B'
C'
与△ABC关于点O中心对称
∴
,
,
,
如图,已知△ABC与△A’B’C’中心对称,求出它们的对称中心O。
A
B
C
A’
B’
C’
解法一:根据观察,B、B’应是对应点,连结BB’,用刻度尺找出BB’的中点O,则点O即为所求(如图)
A
B
C
A’
B’
C’
O
O
解法二:根据观察,B、B’及C、C’应是两组对应点,连结BB’、CC’,BB’、CC’相交于点O,则点O即为所求(如图)。
A
B
C
A’
B’
C’
动手设计,迁移应用
A
O
A′
初级:点的中心对应点的作法
点A′即为所求的点
已知A点和O点,画出点A关于点O的对应点A'
A
A′
B′
B
O
中级:线段的中心对称线段的作法
已知线段AB和O点,画出线段AB关于点O
的对
称线段A'B'
线段A′
B′为所求作的线段
如图,选择点O为对称中心,画出与
△ABC关于点O对称的△A′B′C′.
A’
C’
B’
△A′B′C′即为所求的三角形.
1.
连接AO并延长到A′,使
OA
′=OA,得到点A的对称点A′.
2.
同样画B、C的对称点
B′、C′.
3.
顺次连接A′、B′、C′各点.
画法:
分析:确定一个三角形需要几个点?作一个三角形关于某点成中心对称的三角形,需要作几个点的对称点呢?
高级
已知四边形ABCD和O点,画出四边形ABCD
关于O点的对称图形。
.
C?
D?
A
B
D
C
O
A?
B?
画法:
1、连结AO
并延长到A?,使OA=OA?,得到点A的对称点A?
.
2、同样画B、C、D的对称点B?、C?、D?
3、顺次连结A?、B?、C?、D?各点
所以,四边形A?B?C?D?就是所求的四边形
画一个与已知四边形ABCD中心对称图形。
(1)以顶点A为对称中心;
(2)以BC边的中点O为对称中心。
D
A
B
C
E
F
G
M
D
A
B
C
O
.
N
先画出图形中的几个关键点(线段的端点、如多边形的顶点、圆的圆心等)关于某点的对称点,然后再顺次连结有关对称点即可。
(1)画一个点关于某点(对称中心)的对称点的画
法是:
先连接这个点与对称中心并延长一倍即可。
(2)画一个图形关于某点的对称图形的画法是:
2、如图,AO=DO,画出这个图形关于点O成中心对称的图形。
技师
3、如图,A、B两点的坐标分别是(3,2),(-4,1),
画出线段AB和它关于坐标原点成中心对称的线段A'B'。
高级技师:
A′
B′
C
′
O
A
B
C
如图,已知等边△ABC和点O,画△
A'
B'
C‘
使△A′B′C′和△ABC关于点O成中心对称.
移动一块正方形
(1)使得到图形只是轴对称图形;
(2)使得到图形只是中心对称图形;
(3)既是轴对称图形又是中心对称图形.
你最棒!
怎样判别两个图形关于某一点成中心对称呢?
如果两个图形的
对应点连成的线
段都经过某一点,
并且被该点平分,
那么这两个图形
一定关于这一点
成中心对称。
这节课你的收获是
你的疑惑
通过本节课的学习你有没有新的想法或发现?你觉得还有什么问题需要继续讨论吗?
讨论:中心对称与轴对称的区别:
轴对称
中心对称
有一条对称轴——直线
图形沿对称轴对折(翻折180°)后重合
折叠后与另一图形重合
对称点的连线被对称轴垂直平分
有一个对称中心——点
图形绕对称中心旋转180°后重合
旋转后与另一图形重合
对称点连线经过对称中心,
且被对称中心平分
课后延伸,实践应用
再见!
