鲁教版(五四制)八上5.1.2 平行四边形的性质 课件(26张)
文档属性
| 名称 | 鲁教版(五四制)八上5.1.2 平行四边形的性质 课件(26张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-02 00:00:00 | ||
图片预览



文档简介
(共26张PPT)
定义:
判定作用:
∴四边形ABCD是平行四边形
AB∥CD
AD∥BC
∵
A
D
B
C
∵四边形ABCD是平行四边形
AB∥CD
AD∥BC
∴
性质作用:
两组对边分别平行的四边形叫平行四边形.
A
D
B
C
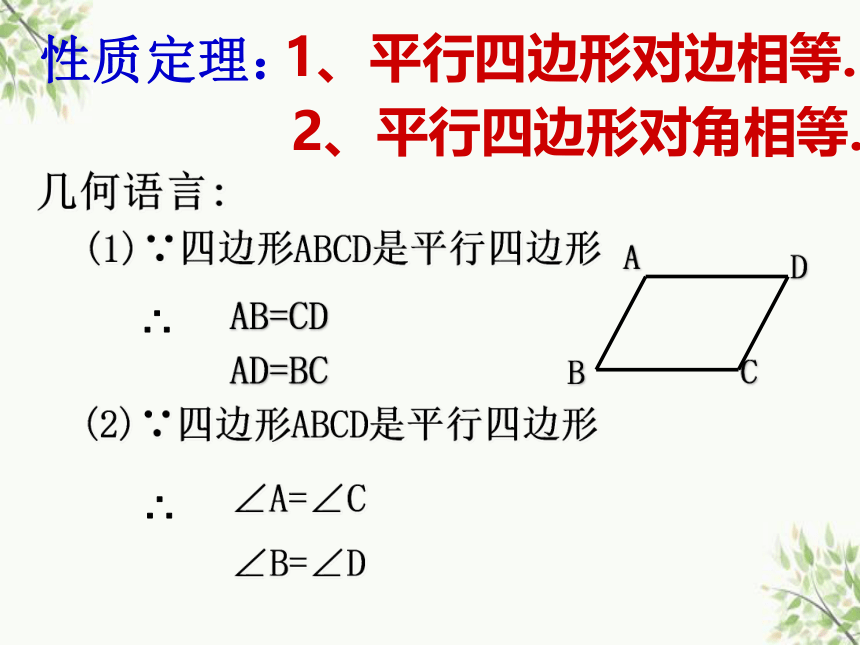
1、平行四边形对边相等.
几何语言:
(1)∵四边形ABCD是平行四边形
AB=CD
AD=BC
∴
(2)∵四边形ABCD是平行四边形
∠A=∠C
∠B=∠D
∴
性质定理:
2、平行四边形对角相等.
●
A
D
O
C
B
D
B
O
C
A
再看一遍
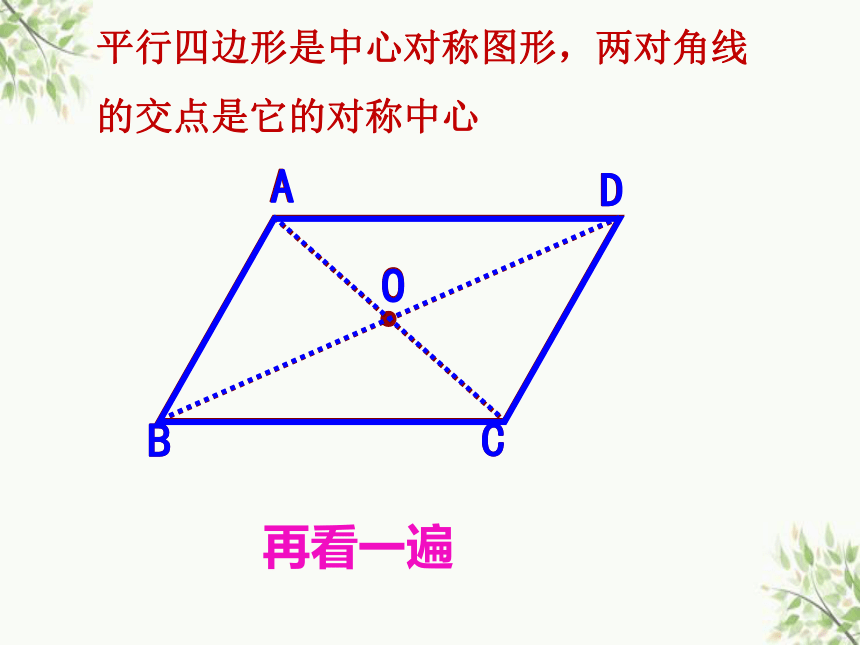
平行四边形是中心对称图形,两对角线
的交点是它的对称中心
●
A
D
O
C
B
D
B
O
C
A
在
ABCD,连接对角线AC,可得△_____≌△_____?
问题情境一
A
D
B
C
A
D
B
C
ABC
CDA
CDB
ABD
连接对角线BD,可得△_____≌△_____?
B
C
D
A
O
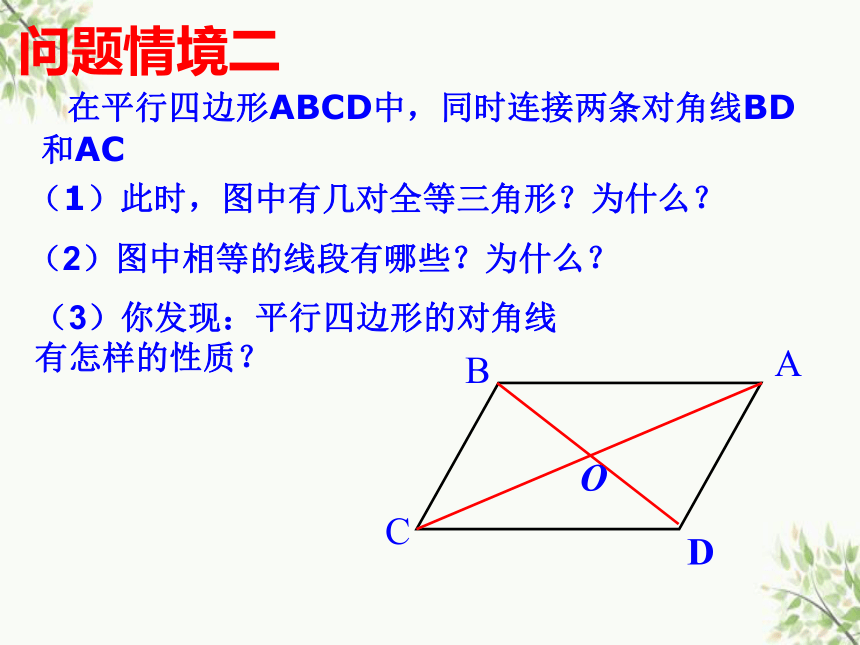
在平行四边形ABCD中,同时连接两条对角线BD和AC
问题情境二
(3)你发现:平行四边形的对角线
有怎样的性质?
(2)图中相等的线段有哪些?为什么?
(1)此时,图中有几对全等三角形?为什么?
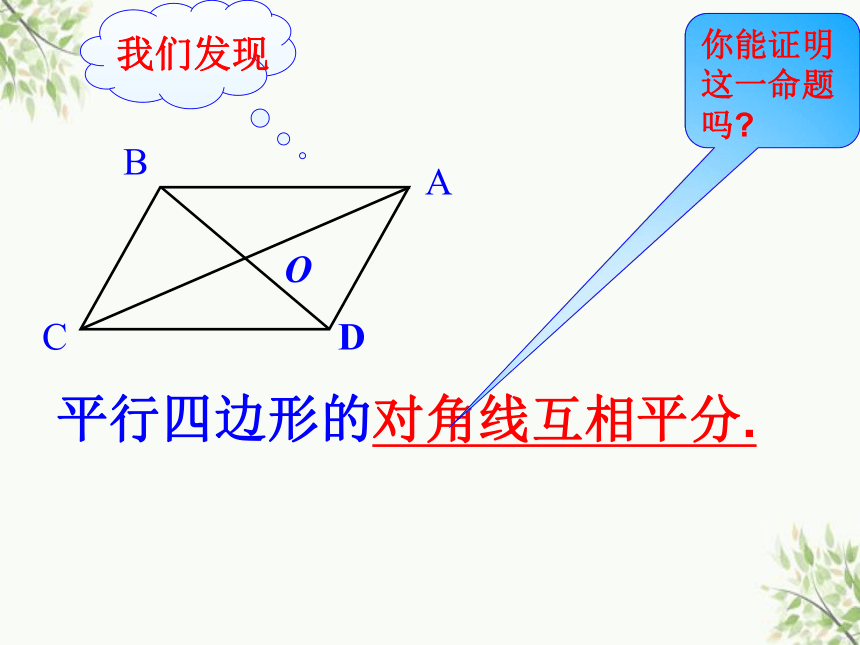
平行四边形的对角线互相平分.
我们发现
A
B
C
D
O
A
C
D
B
O
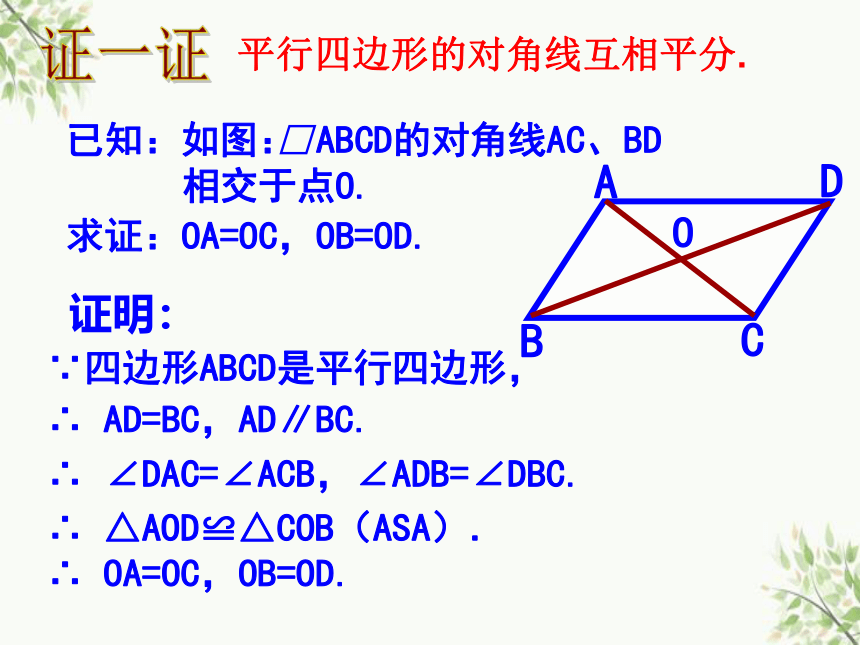
已知:如图:
ABCD的对角线AC、BD
相交于点O.
求证:OA=OC,OB=OD.
证明:
∵四边形ABCD是平行四边形,
∴
AD=BC,AD∥BC.
∴
∠DAC=∠ACB,∠ADB=∠DBC.
∴
△AOD≌△COB(ASA).
∴
OA=OC,OB=OD.
平行四边形的对角线互相平分.
平行四边形的性质定理:
3、平行四边形的对角线互相平分。
我收获
希望
付出
收获
已知
平行四边形ABCD的两条对角线相交
于点O,OD=3,OA=4,AD=5,则
OB=
_____
OC=
_____
3
4
已知
平行四边形ABCD的两条对角线相交
于点O,OD=3,OA=4,AD=5,则
OB=
_____OC=
____;
探究升级:平行四边形ABCD的周长为____
4
3
20
O
D
B
A
C
如图,在
ABCD中,
对角线AC﹑BD相交于点O,且AC=16,BD=24,AD=13,
则△OBC的周长等于______.
33
O
D
B
A
C
如图,在
ABCD中,
对角线AC﹑BD相交于点O,且AC=16,BD=24,AD=13,
则△OBC的周长等于______.
探究升级:
33
44
若△OBC的周长比△OAB的周长大4,则
ABCD的周长为______
已知
平行四边形ABCD的两条对角线相交
于点O,OD=3,OA=5,AD=4,
则:BD=__
;
6
已知:
平行四边形ABCD的两条对角线相交
于点O,OD=3,OA=5,AD=4,则
BD=_;
探究升级:
此时S△
ADO=__
,S
ABCD=__
6
24
6
三角形的中线等分三角形的面积
A
B
C
D
F
E
O
问题情境三:已知:
ABCD的对角线AC,BD交于点O.过点O作直线EF,分别交AB,CD于点E,F。
(3)请你证明OE=OF。
(1)比较情境二,图中又多了几对全等三角形?理由是?
(2)
相等的线段又多了几对?
(合作学习任务:先自主完成,再组内交流,后小组展示)
A
B
D
O
E
F
A
B
C
D
O
E
F
A
B
C
D
O
E
F
C
变式一:改变直线EF的位置,OE=OF还成立吗?
变式二:若直线EF与一组对边的延长线相交,此时,OE=OF还成立吗?
A
B
C
D
O
E
F
E
F
●
O
D
C
B
A
●
O
D
C
B
A
●
O
D
C
B
A
E
F
●
●
●
●
过平行四边形的对角线交点作直线与平行四边形的一组对边或对边的延长线相交,得到线段被对角线的交点平分。
变式三:
你认为:直线EF将平行四边形分成的两部分的面积有怎样的关系?为什么?
过对角线交点的任一条直线都将平行四边形分成面积相等的两部分
A
B
C
D
O
E
F
B
A
C
D
(F)
(E)
能
力
提
升
希望
小结
付出
收获…
平行四边形的性质
边
角
对角线
中心对称图形
基本图形
对边平行且相等
对角相等,
(邻角互补)
对角线互相平分
O
D
B
A
C
O
D
B
A
C
转化思想
四边形
三角形
基本思想
请你来设计:我校有一块平行四边形的草地,想在中间留一条小路,把它分成面积相等的两块,请你来想想,可以怎样分?有多少种分法?
谢谢同学们!
定义:
判定作用:
∴四边形ABCD是平行四边形
AB∥CD
AD∥BC
∵
A
D
B
C
∵四边形ABCD是平行四边形
AB∥CD
AD∥BC
∴
性质作用:
两组对边分别平行的四边形叫平行四边形.
A
D
B
C
1、平行四边形对边相等.
几何语言:
(1)∵四边形ABCD是平行四边形
AB=CD
AD=BC
∴
(2)∵四边形ABCD是平行四边形
∠A=∠C
∠B=∠D
∴
性质定理:
2、平行四边形对角相等.
●
A
D
O
C
B
D
B
O
C
A
再看一遍
平行四边形是中心对称图形,两对角线
的交点是它的对称中心
●
A
D
O
C
B
D
B
O
C
A
在
ABCD,连接对角线AC,可得△_____≌△_____?
问题情境一
A
D
B
C
A
D
B
C
ABC
CDA
CDB
ABD
连接对角线BD,可得△_____≌△_____?
B
C
D
A
O
在平行四边形ABCD中,同时连接两条对角线BD和AC
问题情境二
(3)你发现:平行四边形的对角线
有怎样的性质?
(2)图中相等的线段有哪些?为什么?
(1)此时,图中有几对全等三角形?为什么?
平行四边形的对角线互相平分.
我们发现
A
B
C
D
O
A
C
D
B
O
已知:如图:
ABCD的对角线AC、BD
相交于点O.
求证:OA=OC,OB=OD.
证明:
∵四边形ABCD是平行四边形,
∴
AD=BC,AD∥BC.
∴
∠DAC=∠ACB,∠ADB=∠DBC.
∴
△AOD≌△COB(ASA).
∴
OA=OC,OB=OD.
平行四边形的对角线互相平分.
平行四边形的性质定理:
3、平行四边形的对角线互相平分。
我收获
希望
付出
收获
已知
平行四边形ABCD的两条对角线相交
于点O,OD=3,OA=4,AD=5,则
OB=
_____
OC=
_____
3
4
已知
平行四边形ABCD的两条对角线相交
于点O,OD=3,OA=4,AD=5,则
OB=
_____OC=
____;
探究升级:平行四边形ABCD的周长为____
4
3
20
O
D
B
A
C
如图,在
ABCD中,
对角线AC﹑BD相交于点O,且AC=16,BD=24,AD=13,
则△OBC的周长等于______.
33
O
D
B
A
C
如图,在
ABCD中,
对角线AC﹑BD相交于点O,且AC=16,BD=24,AD=13,
则△OBC的周长等于______.
探究升级:
33
44
若△OBC的周长比△OAB的周长大4,则
ABCD的周长为______
已知
平行四边形ABCD的两条对角线相交
于点O,OD=3,OA=5,AD=4,
则:BD=__
;
6
已知:
平行四边形ABCD的两条对角线相交
于点O,OD=3,OA=5,AD=4,则
BD=_;
探究升级:
此时S△
ADO=__
,S
ABCD=__
6
24
6
三角形的中线等分三角形的面积
A
B
C
D
F
E
O
问题情境三:已知:
ABCD的对角线AC,BD交于点O.过点O作直线EF,分别交AB,CD于点E,F。
(3)请你证明OE=OF。
(1)比较情境二,图中又多了几对全等三角形?理由是?
(2)
相等的线段又多了几对?
(合作学习任务:先自主完成,再组内交流,后小组展示)
A
B
D
O
E
F
A
B
C
D
O
E
F
A
B
C
D
O
E
F
C
变式一:改变直线EF的位置,OE=OF还成立吗?
变式二:若直线EF与一组对边的延长线相交,此时,OE=OF还成立吗?
A
B
C
D
O
E
F
E
F
●
O
D
C
B
A
●
O
D
C
B
A
●
O
D
C
B
A
E
F
●
●
●
●
过平行四边形的对角线交点作直线与平行四边形的一组对边或对边的延长线相交,得到线段被对角线的交点平分。
变式三:
你认为:直线EF将平行四边形分成的两部分的面积有怎样的关系?为什么?
过对角线交点的任一条直线都将平行四边形分成面积相等的两部分
A
B
C
D
O
E
F
B
A
C
D
(F)
(E)
能
力
提
升
希望
小结
付出
收获…
平行四边形的性质
边
角
对角线
中心对称图形
基本图形
对边平行且相等
对角相等,
(邻角互补)
对角线互相平分
O
D
B
A
C
O
D
B
A
C
转化思想
四边形
三角形
基本思想
请你来设计:我校有一块平行四边形的草地,想在中间留一条小路,把它分成面积相等的两块,请你来想想,可以怎样分?有多少种分法?
谢谢同学们!
