鲁教版(五四制)八上5.2.1平行四边形判定 课件(17张)
文档属性
| 名称 | 鲁教版(五四制)八上5.2.1平行四边形判定 课件(17张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 920.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-02 17:42:52 | ||
图片预览

文档简介
(共17张PPT)
鲁教版第五章
新授课
A
B
C
D
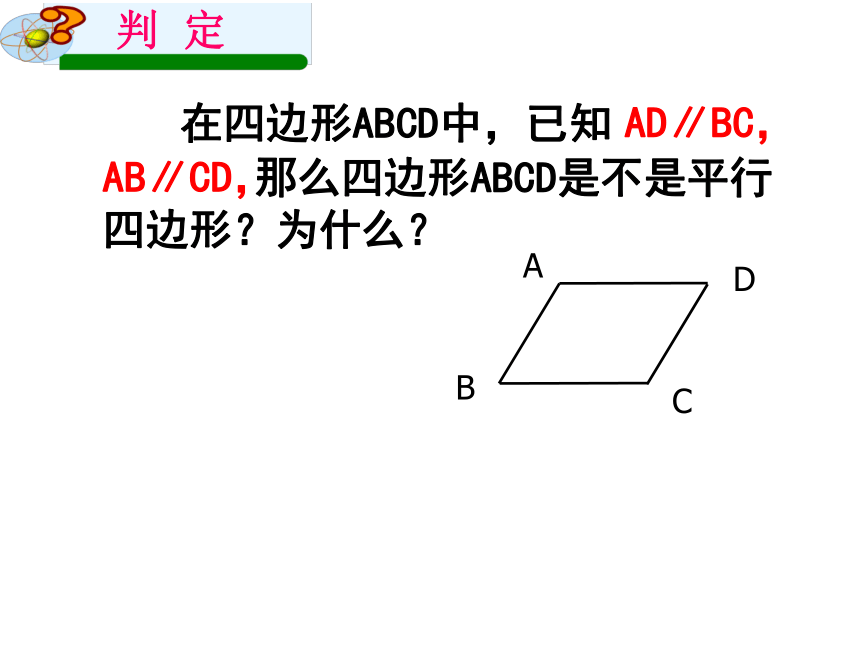
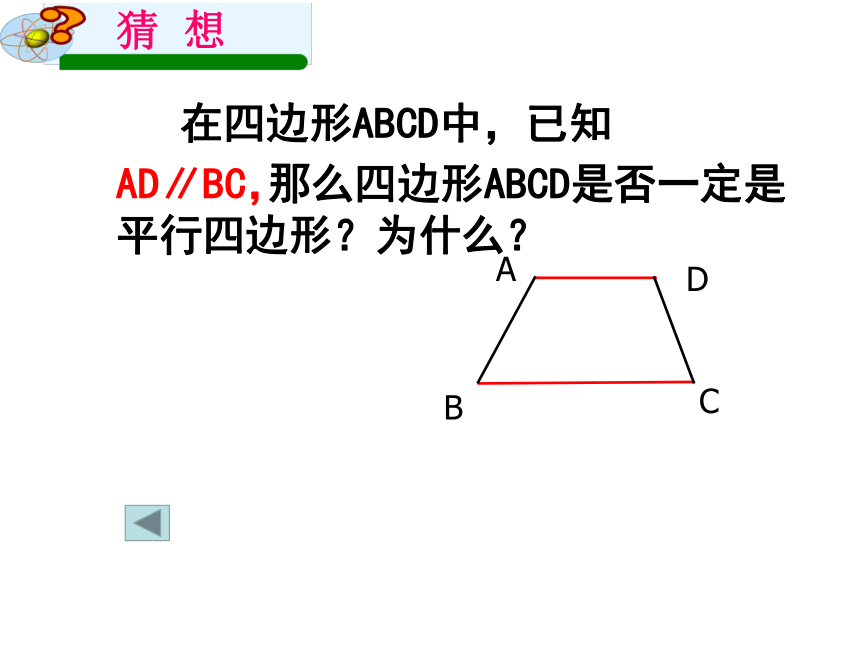
在四边形ABCD中,已知
判
定
AB∥CD,
AD∥BC,
那么四边形ABCD是不是平行四边形?为什么?
AB∥CD,
AD∥BC,
A
D
B
C
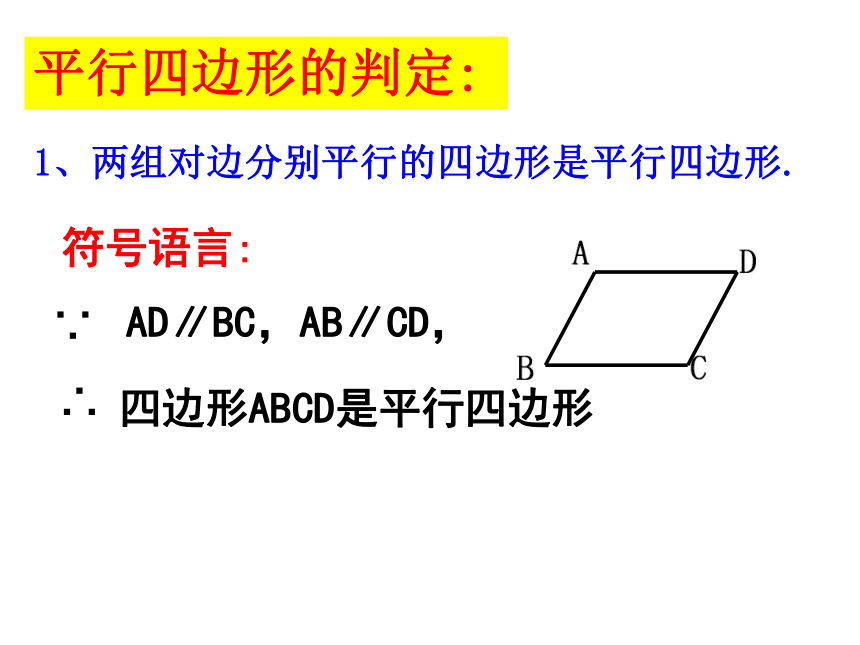
平行四边形的判定:
1、两组对边分别平行的四边形是平行四边形.
符号语言:
∵
∴
四边形ABCD是平行四边形
A
B
C
D
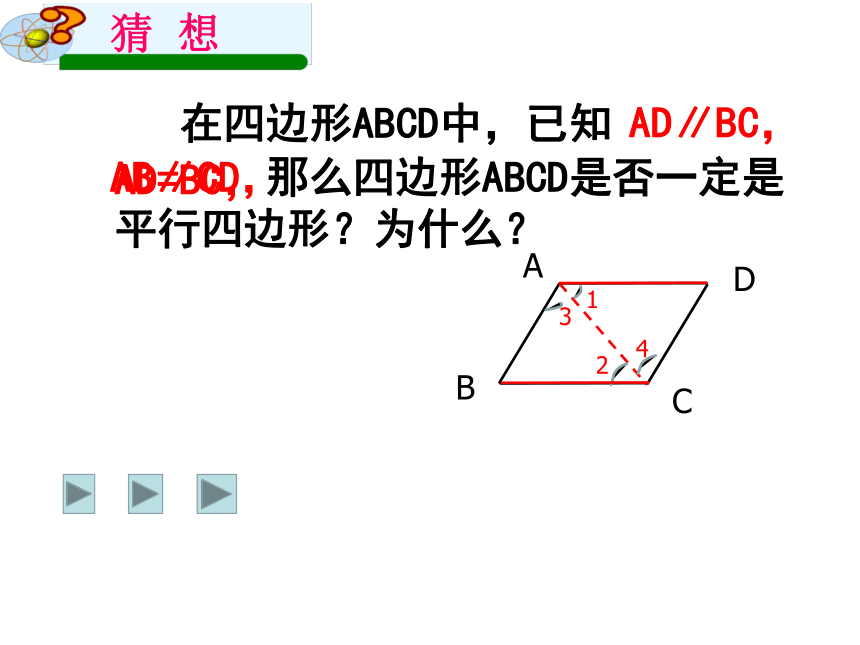
在四边形ABCD中,已知
猜
想
AB∥CD,
AD∥BC,
那么四边形ABCD是否一定是平行四边形?为什么?
AD=BC,
1
2
3
4
A
B
C
D
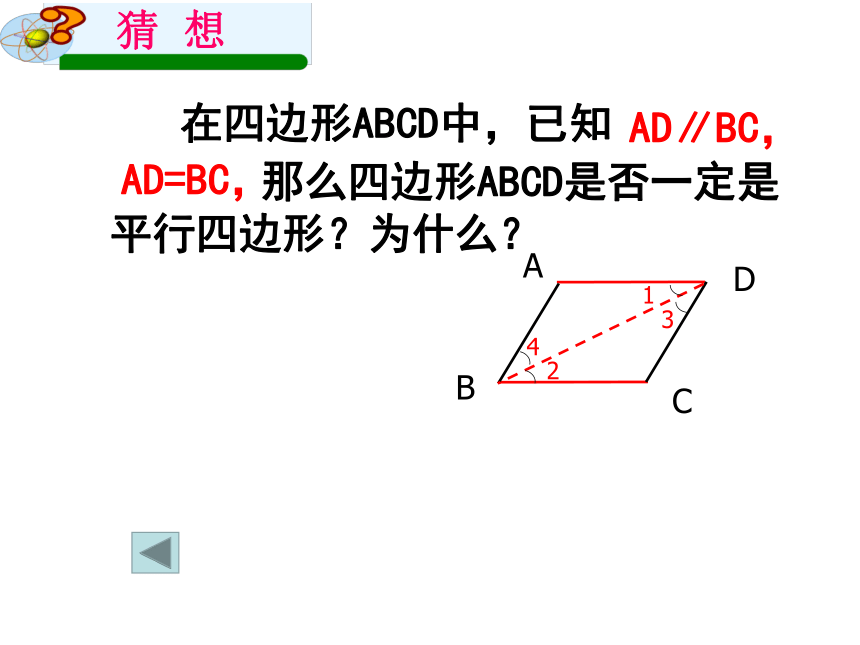
在四边形ABCD中,已知
猜
想
AD∥BC,
那么四边形ABCD是否一定是平行四边形?为什么?
AD=BC,
4
1
3
2
A
B
C
D
在四边形ABCD中,已知
猜
想
AD∥BC,
那么四边形ABCD是否一定是平行四边形?为什么?
∵AD∥BC,AD=BC,
A
D
B
C
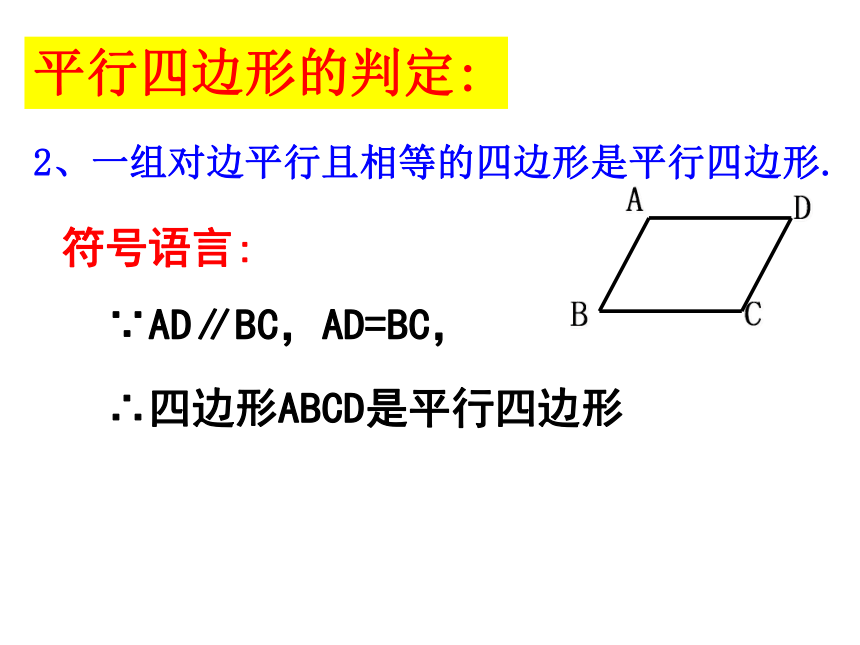
平行四边形的判定:
2、一组对边平行且相等的四边形是平行四边形.
符号语言:
∴四边形ABCD是平行四边形
我们改变四边形的条件构造平行四边形,找到了一个判定平行四边形的方法.还有没有别的判定方法呢?请同学们前后两排六人为一组,用吸管来作四边形的边或对角线,看看在什么条件下还能构成平行四边形。
做一做
A
D
B
C
平行四边形的判定:
2、一组对边平行且相等的四边形是平行四边形.
1、两组对边分别平行的四边形是平行四边形.
3、两组对边分别相等的四边形是平行四边形.
4、两组对角分别相等的四边形是平行四边形.
5、对角线互相平分的四边形是平行四边形.
A
D
B
C
O
定理应用
例:已知:如图,
E、F是
ABCD对角线AC
上的两点,并且AE=CF.
求证:四边形BFDE是平行四边形.
E
A
D
B
C
F
O
巩固提高
导学案:当堂检测
巩固提高
当堂检测:
1、在四边形ABCD中,AB=2x+3,AD=3y-1,CD=y+4,BC=x+6,要使四边形ABCD为平行四边形,则x,y的值为
(
A
)
A.
x=2,y=3
B.x=3,y=2
C.x=5,y=3
D.x=3,y=2.5
2、在四边形ABCD中,已知∠A=50°,∠B=130°,则∠C=
50°
,∠D=
130°时,四边形ABCD是平行四边形。
3、不能判断四边形ABCD是平行四边形的是(
C
)
A.AB=CD,AD=BC
B.AB=CD,AB∥CD
C.AB=CD,AD∥BC
D.AB∥CD,AD∥BC
4、如图所示,四边形ABCD的对角线AC和BD相交于点O,下列判断正确的是
(
D
)
A.若AO=OC,则四边形ABCD是平行四边形
B.若AC=BD,则四边形ABCD是平行四边形
C.若AO=BO,CO=DO,则四边形ABCD是平行四边形
D.若AO=OC,BO=OD,则四边形ABCD是平行四边形
通过这节课的学习,
你有哪些收获?能与大家一起分享吗?
丰
收
园
导学案:149页日清
作
业
A
B
C
D
O
边:
①AB=CD
②AD=BC
,③AB∥CD
④AD∥BC
角:
⑤∠BAD=∠BCD
⑥∠ABC=∠ADC
对角线:⑦OA=OC
⑧OB=OD
在
ABCD中,
反之,在这8个条件中任选2个,能证明
四边形ABCD是平行四边形的有________.
想一想
平行四边形的性质:
平行四边形的对边平行且相等。
边
角
平行四边形的对角相等.
对称性
平行四边形是中心对称图形,两条
对角线的交点是它的对称中心。
平行四边形的对角线互相平分.
对角线
复
习
鲁教版第五章
新授课
A
B
C
D
在四边形ABCD中,已知
判
定
AB∥CD,
AD∥BC,
那么四边形ABCD是不是平行四边形?为什么?
AB∥CD,
AD∥BC,
A
D
B
C
平行四边形的判定:
1、两组对边分别平行的四边形是平行四边形.
符号语言:
∵
∴
四边形ABCD是平行四边形
A
B
C
D
在四边形ABCD中,已知
猜
想
AB∥CD,
AD∥BC,
那么四边形ABCD是否一定是平行四边形?为什么?
AD=BC,
1
2
3
4
A
B
C
D
在四边形ABCD中,已知
猜
想
AD∥BC,
那么四边形ABCD是否一定是平行四边形?为什么?
AD=BC,
4
1
3
2
A
B
C
D
在四边形ABCD中,已知
猜
想
AD∥BC,
那么四边形ABCD是否一定是平行四边形?为什么?
∵AD∥BC,AD=BC,
A
D
B
C
平行四边形的判定:
2、一组对边平行且相等的四边形是平行四边形.
符号语言:
∴四边形ABCD是平行四边形
我们改变四边形的条件构造平行四边形,找到了一个判定平行四边形的方法.还有没有别的判定方法呢?请同学们前后两排六人为一组,用吸管来作四边形的边或对角线,看看在什么条件下还能构成平行四边形。
做一做
A
D
B
C
平行四边形的判定:
2、一组对边平行且相等的四边形是平行四边形.
1、两组对边分别平行的四边形是平行四边形.
3、两组对边分别相等的四边形是平行四边形.
4、两组对角分别相等的四边形是平行四边形.
5、对角线互相平分的四边形是平行四边形.
A
D
B
C
O
定理应用
例:已知:如图,
E、F是
ABCD对角线AC
上的两点,并且AE=CF.
求证:四边形BFDE是平行四边形.
E
A
D
B
C
F
O
巩固提高
导学案:当堂检测
巩固提高
当堂检测:
1、在四边形ABCD中,AB=2x+3,AD=3y-1,CD=y+4,BC=x+6,要使四边形ABCD为平行四边形,则x,y的值为
(
A
)
A.
x=2,y=3
B.x=3,y=2
C.x=5,y=3
D.x=3,y=2.5
2、在四边形ABCD中,已知∠A=50°,∠B=130°,则∠C=
50°
,∠D=
130°时,四边形ABCD是平行四边形。
3、不能判断四边形ABCD是平行四边形的是(
C
)
A.AB=CD,AD=BC
B.AB=CD,AB∥CD
C.AB=CD,AD∥BC
D.AB∥CD,AD∥BC
4、如图所示,四边形ABCD的对角线AC和BD相交于点O,下列判断正确的是
(
D
)
A.若AO=OC,则四边形ABCD是平行四边形
B.若AC=BD,则四边形ABCD是平行四边形
C.若AO=BO,CO=DO,则四边形ABCD是平行四边形
D.若AO=OC,BO=OD,则四边形ABCD是平行四边形
通过这节课的学习,
你有哪些收获?能与大家一起分享吗?
丰
收
园
导学案:149页日清
作
业
A
B
C
D
O
边:
①AB=CD
②AD=BC
,③AB∥CD
④AD∥BC
角:
⑤∠BAD=∠BCD
⑥∠ABC=∠ADC
对角线:⑦OA=OC
⑧OB=OD
在
ABCD中,
反之,在这8个条件中任选2个,能证明
四边形ABCD是平行四边形的有________.
想一想
平行四边形的性质:
平行四边形的对边平行且相等。
边
角
平行四边形的对角相等.
对称性
平行四边形是中心对称图形,两条
对角线的交点是它的对称中心。
平行四边形的对角线互相平分.
对角线
复
习
