鲁教版 五四学制 八年级上册 数学 导学案 第三章 数据的分析3.3 从统计图分析数据的集中趋势(无答案)
文档属性
| 名称 | 鲁教版 五四学制 八年级上册 数学 导学案 第三章 数据的分析3.3 从统计图分析数据的集中趋势(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 631.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-02 00:00:00 | ||
图片预览


文档简介
3
从统计图分析数据的集中趋势
学习目标
会通过三种统计图进行数据分析,并求出相应的平均数、众数、中位数.
在具体情境中进一步体会平均数、中位数和众数的意义和差别,学会选择恰当的数据代表解决问题.
课前预习
旧知复习
1.一般来讲,我们常见的统计图有
、
、
.
2.
、
、
都是描述数据集中趋势的统计量.
三种统计图的优点:
折线统计图:
.
条形统计图:
.
扇形统计图:
.
自主预习
观察课本57页图3-1,回答下列问题,:
本次检测的10个面包质量的众数是
.平均数是
.
观察课本58页图3-2,回答下列问题:
(1)甲队队员年龄的众数是
,中位数
,是平均数是
.
(2)乙队队员年龄的众数是
,中位数
,是平均数是
.
(3)丙队队员年龄的众数是
,中位数
,是平均数是
.
3.
观察课本58页图3-3,回答下列问题:
(1)本次调查的20名同学,本学期计划购买课外书的花费的众数是
,平均数是
.
(2)在上面的问题中,如果不知道调查的总人数,你还能求平均数吗?为什么?
尝试练习
1.某校八年级一班班长统计,去年1月到八月校园文化活动中,全班同学的课外阅读数量单位本绘制的如图所示的折线统计图这组数据的中位数是
.
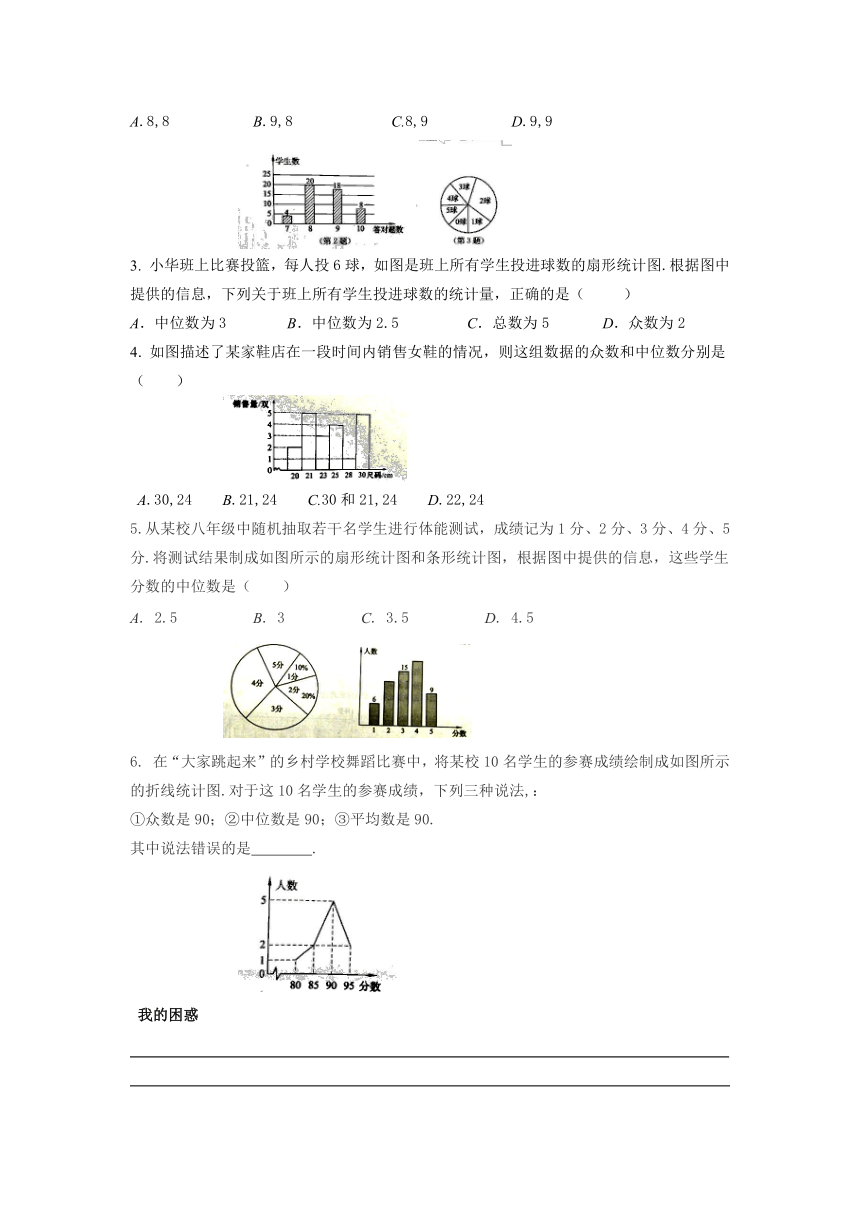
2.数学老师布置了10道选择题作为练课堂练习,课代表将全班答题情况绘制成如图所示的条形统计图,根据此图可知,每位同学答对的题数所组成样本的中位数和众数分别为(
)
A.8,8
B.9,8
C.8,9
D.9,9
3.
小华班上比赛投篮,每人投6球,如图是班上所有学生投进球数的扇形统计图.根据图中提供的信息,下列关于班上所有学生投进球数的统计量,正确的是(
)
A.中位数为3
B.中位数为2.5
C.总数为5
D.众数为2
4.
如图描述了某家鞋店在一段时间内销售女鞋的情况,则这组数据的众数和中位数分别是(
)
A.30,24
B.21,24
C.30和21,24
D.22,24
5.从某校八年级中随机抽取若干名学生进行体能测试,成绩记为1分、2分、3分、4分、5分.将测试结果制成如图所示的扇形统计图和条形统计图,根据图中提供的信息,这些学生分数的中位数是(
)
A.
2.5
B.
3
C.
3.5
D.
4.5
6.
在“大家跳起来”的乡村学校舞蹈比赛中,将某校10名学生的参赛成绩绘制成如图所示的折线统计图.对于这10名学生的参赛成绩,下列三种说法,:
①众数是90;②中位数是90;③平均数是90.
其中说法错误的是
.
我的困惑
课中导学
典型例题
某中学在一次爱心捐款活动中,全体同学积极踊跃捐款,抽查了九年级一班全班学生捐款情况,并绘制了如下的统计表和统计图:
捐款(元)
20
50
100
150
200
人数(人)
4
12
9
3
2
(1)本次接受随机抽样调查的学生人数为
.扇形统计图中的m=
。n=
;
(2)求学生捐款数目的众数、中位数和平均数;
(3)若该校有学生2500人,估计该校学生共捐款多少元?
解:(1)本次接受随机抽样调查的学生人数为4+12+9+3+2=30(人).
12÷30=40%,9÷30=30%.
所以扇形统计图中的m=40,n=30;
(2)∵在这组数据中,50出现了12次,次数最多,
∴学生捐款数目的众数是50;
∵按照从小到大排列,处于中间位置的两个数据都是50.
∴中位数为50;
这组数据的平均数=(20×4+50×12+100×9+150×3+200×2)÷30=2430÷30=81.
(3)2500×81=202500(元).
答;估计该校学生共捐款202500元.
园丁点拨:(1)把表格中的数据相加得出本次接受随机抽样调查的学生人数:利用50元、100元的捐款人数求得占总数的百分比得出m,n的数值即可;
(2)利用众数、中位数和平均数的意义和求法分别得出答案即可;
(3)利用求得的平均数乘总人数得出答案即可.
为了解学生的课外阅读情况,李老师随机调查了一部分学生,得到了他们上周双休日课外阅读时间(记为t,单位h)的一组样本数据,其部分条形图和扇形图如下:
请补全条形图和扇形图.
试确定这组样本数据的中位数和众数.
估计全班学生上周双休日的平均课外阅读时间.
解:(1)由条形统计图知,读1小时的人数为3人,在扇形统计图中占的比例为12%,所以总调查人数=312%=25人.所以读2小时的人数=25×16%=4人,读3小时的人数=25×24%=6人,读4小时的人数占的比例=7÷25=28%,在扇形统计图中的圆心角=360°×28%=100.8°,读5小时的人数占的比例=1-28%-24%-16%-12%-8%=12%,读5小时的人数=25×12%=3人.
条形图如图所示:
(2)中位数是3(h),众数是4(h);
(3)1×12%+2×16%+3×24%+4×28%+5×12%+6×8%=3.36(h).
估计全班学生上周双休日的平均课外阅读时间为3.36h.
园丁点拨:
(1)由条形统计图知:读1小时的人数为3人,在扇形统计图中占的比例为12%,则总调查人数可求出.这样可分别求出读2小时的人数,读3小时的人数,以及读4小时的人数占的比例,再计算其在扇形统计图中的圆心角.最后求出读5小时的人数占的比例和读5小时的人数;(2)根据中位数和众数的定义解答.(3)根据平均数的定义计算即可.本题还考查了从统计图中获取信息的能力.
变式训练
1.为了宣传节约用水,小明随机调查了某小区部分家庭5月份的用水情况,并将收集的数据整理成如图所示的统计图.
(1)小明一共调查了多少户家庭?
(2)求所调查家庭5月份用水量的众数、平均数.
(3)若该小区有400户居民,请你估计这个小区5月份的用水量.
2.
在学校组织的“做文明市民”知识竞赛中,每班参加比赛的人数相同,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为100分,,90分,80分,70分,学校将某年级的一班和二班的成绩整理并绘制成如图所示的统计图.
请你根据以上提供的信息解答下列问题:
(1)此次竞赛中二班成绩在C级以上(包括C级)的人数为
.
(2)请你将表格补充完整:
平均数/分
中位数/分
众数/分
一班
87.6
90
二班
87.6
100
(3)请从下列不同角度对这次竞赛成绩的结果进行分析:
|①从平均数和中位数的角度来比较一班和二班的成绩;
②从平均数和众数的角度来比较一班和二班的成绩;
③从B级以上(包括B级)的人数的角度来比较一班和二班的成绩.
课后巩固
基础巩固
1.
某校男子足球队的年龄分布如条形图所示,则这些队员年龄的众数是(
)
A.12岁
B.13岁
C.14岁
D.15岁
2.
某市6月份日平均气温统计如图所示,则在日平均气温这组数据中,众数和中位数分别是(
)
A.21,21
B.21,21.5
C.21,22
D.22,22
3.学校快餐店有2元、3元、4元三种价格的饭菜供师生选择(每人限购一份),如图是某月的销售情况统计图,则该校师生购买饭菜费用的平均数和众数分别是(
)
A.2.95元,3元
B.3元,3元
C.3元,4元
D.2.95元,4元
4.某校八年级一班40名学生进行了一次数学测验,成绩整理后分成五组,绘制成频数分布直方图(如图所示),求这40名学生这次数学测验成绩的平均分约为多少分?
能力提升
1.
甲、乙两人在相同的条件下各射靶10次,成绩如图.
(1)甲、乙两人射靶的平均成绩各是多少?
(2)甲、乙两人射靶的中位数各是多少?
(3)甲、乙两人射靶的众数各是多少?
(4)如果你是教练,将选谁去参加比赛?说说你的理由.
小亮和小莹自制了一个标靶进行掷飞镖比赛,两人各掷了10次,下图是他们成绩的统计图.
根据图中信息填写下表:
平均数
中位数
众数
小亮
7
小莹
7
9
(2)
分别用平均数和中位数解释谁的成绩比较好.
3.
某校对九年级学生进行了一次数学学业水平测试,成绩评定分为
A,B,C,D四个等级(注:等级A,B,C,D分别代表优秀、良好、合格、不
合格).学校从九年级学生中随机抽取50名学生的数学成绩进行统计
分析,并绘制成扇形统计图(如图所示).
根据图中所给的信息回答下列问题:
(1)随机抽取的九年级学生数学学业水平测试中,D等级人数的百分率和D等级学生人数分别是多少?
(2)这次随机抽样中,学生数学学业水平测试成绩的中位数落在哪个等级?
(3)若该校九年级学生有800名,请你估计这次数学学业水平测试中,成绩达合格以上(含合格)的人数大约有多少人?
为了倡导“节约用水,从我做起”,某市政府决定对市直机关500户家庭的用水情况做一次调查,是政府调查小组随机抽查了其中的100户家庭一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.
请将条形统计图补充完整;
求这100个样本数据的平均数、众数和中位数;
根据样本数据,估计该市直机关500户家庭中月平均用水量不超过12吨的约有多少户?
从统计图分析数据的集中趋势
学习目标
会通过三种统计图进行数据分析,并求出相应的平均数、众数、中位数.
在具体情境中进一步体会平均数、中位数和众数的意义和差别,学会选择恰当的数据代表解决问题.
课前预习
旧知复习
1.一般来讲,我们常见的统计图有
、
、
.
2.
、
、
都是描述数据集中趋势的统计量.
三种统计图的优点:
折线统计图:
.
条形统计图:
.
扇形统计图:
.
自主预习
观察课本57页图3-1,回答下列问题,:
本次检测的10个面包质量的众数是
.平均数是
.
观察课本58页图3-2,回答下列问题:
(1)甲队队员年龄的众数是
,中位数
,是平均数是
.
(2)乙队队员年龄的众数是
,中位数
,是平均数是
.
(3)丙队队员年龄的众数是
,中位数
,是平均数是
.
3.
观察课本58页图3-3,回答下列问题:
(1)本次调查的20名同学,本学期计划购买课外书的花费的众数是
,平均数是
.
(2)在上面的问题中,如果不知道调查的总人数,你还能求平均数吗?为什么?
尝试练习
1.某校八年级一班班长统计,去年1月到八月校园文化活动中,全班同学的课外阅读数量单位本绘制的如图所示的折线统计图这组数据的中位数是
.
2.数学老师布置了10道选择题作为练课堂练习,课代表将全班答题情况绘制成如图所示的条形统计图,根据此图可知,每位同学答对的题数所组成样本的中位数和众数分别为(
)
A.8,8
B.9,8
C.8,9
D.9,9
3.
小华班上比赛投篮,每人投6球,如图是班上所有学生投进球数的扇形统计图.根据图中提供的信息,下列关于班上所有学生投进球数的统计量,正确的是(
)
A.中位数为3
B.中位数为2.5
C.总数为5
D.众数为2
4.
如图描述了某家鞋店在一段时间内销售女鞋的情况,则这组数据的众数和中位数分别是(
)
A.30,24
B.21,24
C.30和21,24
D.22,24
5.从某校八年级中随机抽取若干名学生进行体能测试,成绩记为1分、2分、3分、4分、5分.将测试结果制成如图所示的扇形统计图和条形统计图,根据图中提供的信息,这些学生分数的中位数是(
)
A.
2.5
B.
3
C.
3.5
D.
4.5
6.
在“大家跳起来”的乡村学校舞蹈比赛中,将某校10名学生的参赛成绩绘制成如图所示的折线统计图.对于这10名学生的参赛成绩,下列三种说法,:
①众数是90;②中位数是90;③平均数是90.
其中说法错误的是
.
我的困惑
课中导学
典型例题
某中学在一次爱心捐款活动中,全体同学积极踊跃捐款,抽查了九年级一班全班学生捐款情况,并绘制了如下的统计表和统计图:
捐款(元)
20
50
100
150
200
人数(人)
4
12
9
3
2
(1)本次接受随机抽样调查的学生人数为
.扇形统计图中的m=
。n=
;
(2)求学生捐款数目的众数、中位数和平均数;
(3)若该校有学生2500人,估计该校学生共捐款多少元?
解:(1)本次接受随机抽样调查的学生人数为4+12+9+3+2=30(人).
12÷30=40%,9÷30=30%.
所以扇形统计图中的m=40,n=30;
(2)∵在这组数据中,50出现了12次,次数最多,
∴学生捐款数目的众数是50;
∵按照从小到大排列,处于中间位置的两个数据都是50.
∴中位数为50;
这组数据的平均数=(20×4+50×12+100×9+150×3+200×2)÷30=2430÷30=81.
(3)2500×81=202500(元).
答;估计该校学生共捐款202500元.
园丁点拨:(1)把表格中的数据相加得出本次接受随机抽样调查的学生人数:利用50元、100元的捐款人数求得占总数的百分比得出m,n的数值即可;
(2)利用众数、中位数和平均数的意义和求法分别得出答案即可;
(3)利用求得的平均数乘总人数得出答案即可.
为了解学生的课外阅读情况,李老师随机调查了一部分学生,得到了他们上周双休日课外阅读时间(记为t,单位h)的一组样本数据,其部分条形图和扇形图如下:
请补全条形图和扇形图.
试确定这组样本数据的中位数和众数.
估计全班学生上周双休日的平均课外阅读时间.
解:(1)由条形统计图知,读1小时的人数为3人,在扇形统计图中占的比例为12%,所以总调查人数=312%=25人.所以读2小时的人数=25×16%=4人,读3小时的人数=25×24%=6人,读4小时的人数占的比例=7÷25=28%,在扇形统计图中的圆心角=360°×28%=100.8°,读5小时的人数占的比例=1-28%-24%-16%-12%-8%=12%,读5小时的人数=25×12%=3人.
条形图如图所示:
(2)中位数是3(h),众数是4(h);
(3)1×12%+2×16%+3×24%+4×28%+5×12%+6×8%=3.36(h).
估计全班学生上周双休日的平均课外阅读时间为3.36h.
园丁点拨:
(1)由条形统计图知:读1小时的人数为3人,在扇形统计图中占的比例为12%,则总调查人数可求出.这样可分别求出读2小时的人数,读3小时的人数,以及读4小时的人数占的比例,再计算其在扇形统计图中的圆心角.最后求出读5小时的人数占的比例和读5小时的人数;(2)根据中位数和众数的定义解答.(3)根据平均数的定义计算即可.本题还考查了从统计图中获取信息的能力.
变式训练
1.为了宣传节约用水,小明随机调查了某小区部分家庭5月份的用水情况,并将收集的数据整理成如图所示的统计图.
(1)小明一共调查了多少户家庭?
(2)求所调查家庭5月份用水量的众数、平均数.
(3)若该小区有400户居民,请你估计这个小区5月份的用水量.
2.
在学校组织的“做文明市民”知识竞赛中,每班参加比赛的人数相同,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为100分,,90分,80分,70分,学校将某年级的一班和二班的成绩整理并绘制成如图所示的统计图.
请你根据以上提供的信息解答下列问题:
(1)此次竞赛中二班成绩在C级以上(包括C级)的人数为
.
(2)请你将表格补充完整:
平均数/分
中位数/分
众数/分
一班
87.6
90
二班
87.6
100
(3)请从下列不同角度对这次竞赛成绩的结果进行分析:
|①从平均数和中位数的角度来比较一班和二班的成绩;
②从平均数和众数的角度来比较一班和二班的成绩;
③从B级以上(包括B级)的人数的角度来比较一班和二班的成绩.
课后巩固
基础巩固
1.
某校男子足球队的年龄分布如条形图所示,则这些队员年龄的众数是(
)
A.12岁
B.13岁
C.14岁
D.15岁
2.
某市6月份日平均气温统计如图所示,则在日平均气温这组数据中,众数和中位数分别是(
)
A.21,21
B.21,21.5
C.21,22
D.22,22
3.学校快餐店有2元、3元、4元三种价格的饭菜供师生选择(每人限购一份),如图是某月的销售情况统计图,则该校师生购买饭菜费用的平均数和众数分别是(
)
A.2.95元,3元
B.3元,3元
C.3元,4元
D.2.95元,4元
4.某校八年级一班40名学生进行了一次数学测验,成绩整理后分成五组,绘制成频数分布直方图(如图所示),求这40名学生这次数学测验成绩的平均分约为多少分?
能力提升
1.
甲、乙两人在相同的条件下各射靶10次,成绩如图.
(1)甲、乙两人射靶的平均成绩各是多少?
(2)甲、乙两人射靶的中位数各是多少?
(3)甲、乙两人射靶的众数各是多少?
(4)如果你是教练,将选谁去参加比赛?说说你的理由.
小亮和小莹自制了一个标靶进行掷飞镖比赛,两人各掷了10次,下图是他们成绩的统计图.
根据图中信息填写下表:
平均数
中位数
众数
小亮
7
小莹
7
9
(2)
分别用平均数和中位数解释谁的成绩比较好.
3.
某校对九年级学生进行了一次数学学业水平测试,成绩评定分为
A,B,C,D四个等级(注:等级A,B,C,D分别代表优秀、良好、合格、不
合格).学校从九年级学生中随机抽取50名学生的数学成绩进行统计
分析,并绘制成扇形统计图(如图所示).
根据图中所给的信息回答下列问题:
(1)随机抽取的九年级学生数学学业水平测试中,D等级人数的百分率和D等级学生人数分别是多少?
(2)这次随机抽样中,学生数学学业水平测试成绩的中位数落在哪个等级?
(3)若该校九年级学生有800名,请你估计这次数学学业水平测试中,成绩达合格以上(含合格)的人数大约有多少人?
为了倡导“节约用水,从我做起”,某市政府决定对市直机关500户家庭的用水情况做一次调查,是政府调查小组随机抽查了其中的100户家庭一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.
请将条形统计图补充完整;
求这100个样本数据的平均数、众数和中位数;
根据样本数据,估计该市直机关500户家庭中月平均用水量不超过12吨的约有多少户?
