华东师大版七上数学 4.1生活中的立体图形 课件(共17张PPT)
文档属性
| 名称 | 华东师大版七上数学 4.1生活中的立体图形 课件(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-04 15:53:21 | ||
图片预览





文档简介
(共17张PPT)
§4.1
生活中的立体图形
你还会再举出一些类似的物体吗?
这些物体与你小学学过的哪些立体图形相类似?
(1)、(2)所表示的立体图形是柱体;(4)、(5)所表示的立体图形是锥体;(3)表示的图形则是球体
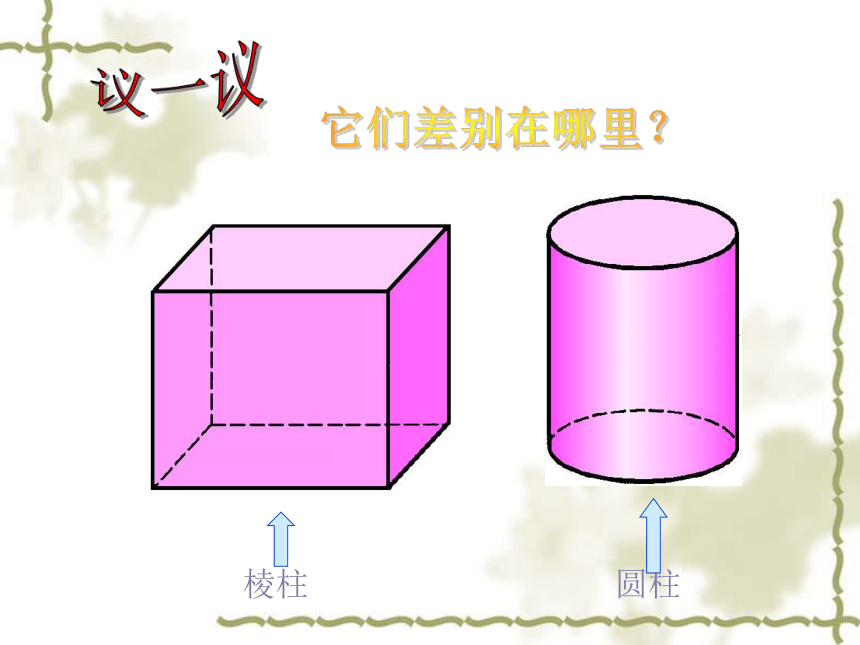
棱柱
圆柱
圆柱与棱柱的相同点与不同点。
几何体
图形
不同点
相同点
圆柱
棱柱
底面是圆;只有一个侧面且为曲面;没有顶点。
底面是多边形;侧面是平面;
有多个顶点。
都有两个底面,且上、下两底面形状和大小完全一样。
想一想
圆柱与圆锥的相同点与不同点。
几何体
图形
不同点
相同点
圆柱
圆锥
有两个大小相同的底面,无顶点。
有一个底面,有一个顶点。
底面都有是圆,侧面都是曲面。
议一议
圆锥
棱锥
…棱柱
…棱锥
你能说出下面图形的名称吗?
2.把图形与对应的图形名称用线连接起来:
圆锥
圆柱
棱柱
棱锥
球
思考:
你能发现上图中的第一个和第五个图形与其他图形的区别吗?
围成立体图形的面是平的面,像这样的立体图形,又称为多面体.
下面的图形是多面体吗?
正四面体
正方体
正八面体
正十二面体
正二十面体
从上面的填表,你发现了什么规律?
伟大的数学家欧拉(Euler
1707—1783)证明了这一令人惊叹的关系式,即欧拉公式:
顶点数+面数-棱数=2.
8
6
6
12
12
12
12
2
2
2
2
8
20
20
30
30
想一想:
判断能否组成一个有22条棱、10个面、15个顶点的棱柱或棱锥?为什么?
可利用欧拉公式进行判断,即:
顶点数+面数-棱数=2.
用六根火柴棒如何搭成四个三角形?
四棱柱
六棱柱
五棱柱
三棱柱
四棱锥
五棱锥
六棱锥
三棱锥
圆锥
棱锥
圆柱
棱柱
柱体
锥体
球体
欧拉公式:
顶点数+面数-棱数=2.
§4.1
生活中的立体图形
你还会再举出一些类似的物体吗?
这些物体与你小学学过的哪些立体图形相类似?
(1)、(2)所表示的立体图形是柱体;(4)、(5)所表示的立体图形是锥体;(3)表示的图形则是球体
棱柱
圆柱
圆柱与棱柱的相同点与不同点。
几何体
图形
不同点
相同点
圆柱
棱柱
底面是圆;只有一个侧面且为曲面;没有顶点。
底面是多边形;侧面是平面;
有多个顶点。
都有两个底面,且上、下两底面形状和大小完全一样。
想一想
圆柱与圆锥的相同点与不同点。
几何体
图形
不同点
相同点
圆柱
圆锥
有两个大小相同的底面,无顶点。
有一个底面,有一个顶点。
底面都有是圆,侧面都是曲面。
议一议
圆锥
棱锥
…棱柱
…棱锥
你能说出下面图形的名称吗?
2.把图形与对应的图形名称用线连接起来:
圆锥
圆柱
棱柱
棱锥
球
思考:
你能发现上图中的第一个和第五个图形与其他图形的区别吗?
围成立体图形的面是平的面,像这样的立体图形,又称为多面体.
下面的图形是多面体吗?
正四面体
正方体
正八面体
正十二面体
正二十面体
从上面的填表,你发现了什么规律?
伟大的数学家欧拉(Euler
1707—1783)证明了这一令人惊叹的关系式,即欧拉公式:
顶点数+面数-棱数=2.
8
6
6
12
12
12
12
2
2
2
2
8
20
20
30
30
想一想:
判断能否组成一个有22条棱、10个面、15个顶点的棱柱或棱锥?为什么?
可利用欧拉公式进行判断,即:
顶点数+面数-棱数=2.
用六根火柴棒如何搭成四个三角形?
四棱柱
六棱柱
五棱柱
三棱柱
四棱锥
五棱锥
六棱锥
三棱锥
圆锥
棱锥
圆柱
棱柱
柱体
锥体
球体
欧拉公式:
顶点数+面数-棱数=2.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
