人教版八上高分笔记之导与练13.1.2.2线段的垂直平分线的作法与应用(原卷+答案)
文档属性
| 名称 | 人教版八上高分笔记之导与练13.1.2.2线段的垂直平分线的作法与应用(原卷+答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-03 06:22:54 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
13.1.2线段的垂直平分线的性质
第2课时
线段的垂直平分线的作法与应用
知识要点:
1.如果两个图形成轴对称,那么其对称轴是任何一对对应点所连线段的??
2.对于轴对称图形,连接任意一对对应点,作所连线段的垂直平分线??,可得到这个轴对称图形的??__________
易错点睛
等腰三角形的对称轴是(?
?)
A.底边上的高
B.底边上的中线
C.顶角的角平分线
D.底边的垂直平分线
【点睛】??对称轴是直线而不是线段。
典型例题:
题型一
利用基本作图解决选址问题
例1、「教材P66习题13.1T12变式题]如图,电信部门要在公路l2同侧、l1异侧的两个城镇A,B之间修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路L1,l2的距离也必须相等,则发射塔C应修建在什么位置?请用尺规作图的方法作出所有符合条件的点C的位置.(不写作法,保留作图痕迹)
变式练习:
如图,A,B表示两个村庄,l表示河流,要在河边修建一个水泵站P,要求水泵站P到村庄A,B的距离相等,用尺规作图的方法作出水泵站P的位置(不写作法,保留作图痕迹)
如图,某校两个班的学生分别在C,D两处参加植树活动,现要在道路AO,OB的交叉区域内设一个茶水供应点M,使点M到两条道路的距离相等,且MD=MC,用尺规作图的方法作出茶水供应点M的位置.(不写作法,保留作图痕迹)
题型二
利用基本作图进行问题探究
例2、如图,已知△ABC和ΔA'B'C'关于直线MN对称,ΔA'B'C'和ΔA"B”C”关于直线EF对称
(1)画出直线EF;(不写作法,保留作图痕迹)
(2)若直线MN与EF相交于点0,试探究∠BOB”与直线MN,EF所夹锐角<α的数量关系.
变式练习:
如图,已知ΔABC.
(1)尺规作图:
①作线段AB的垂直平分线l;
②作射线CM平分∠ACB,与直线l交于点D,连接AD,BD.(不写作法,保留作图痕迹)
(2)在(1)的条件下,∠ACB和∠ADB的数量关系为
?
(3)证明你所发现的(2)中的结论.
基础练习:
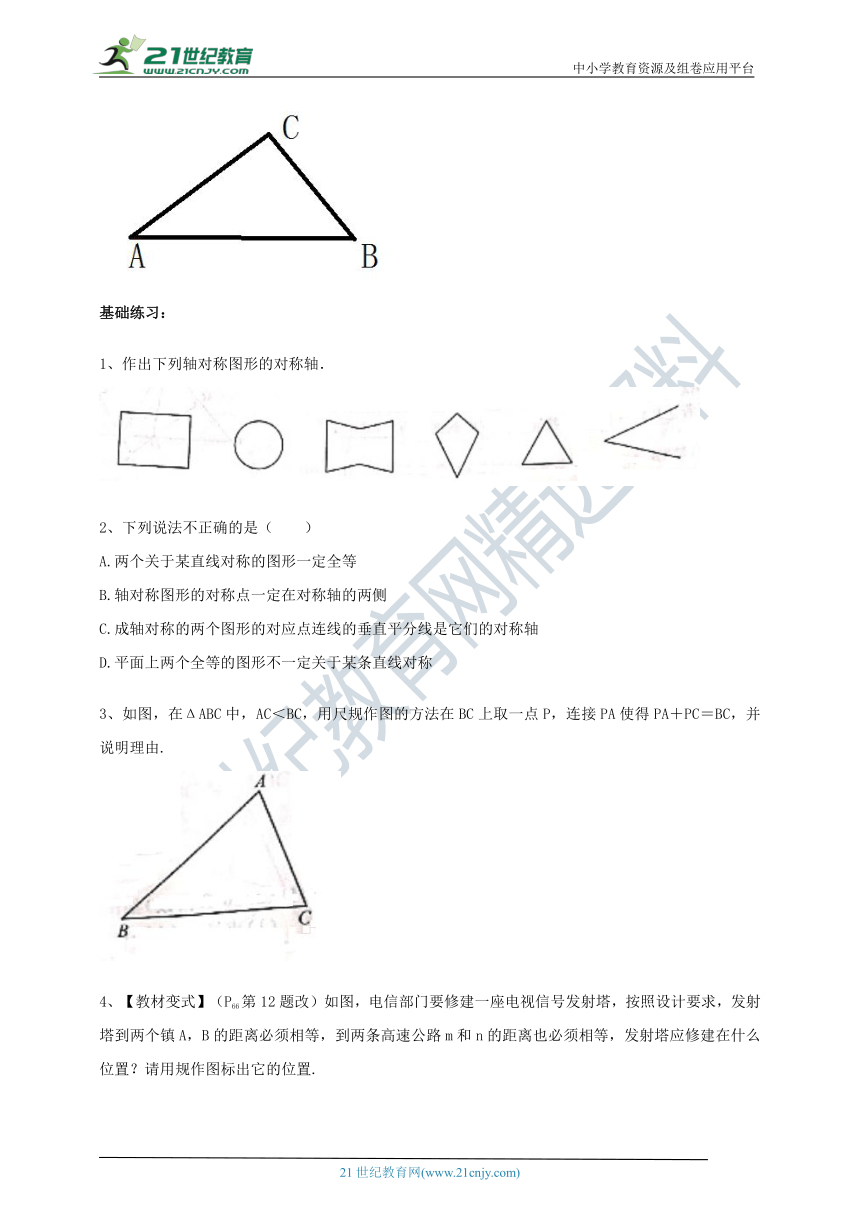
作出下列轴对称图形的对称轴.
2、下列说法不正确的是(
)
A.两个关于某直线对称的图形一定全等
B.轴对称图形的对称点一定在对称轴的两侧
C.成轴对称的两个图形的对应点连线的垂直平分线是它们的对称轴
D.平面上两个全等的图形不一定关于某条直线对称
3、如图,在ΔABC中,AC<BC,用尺规作图的方法在BC上取一点P,连接PA使得PA+PC=BC,并说明理由.
4、【教材变式】(P66第12题改)如图,电信部门要修建一座电视信号发射塔,按照设计要求,发射塔到两个镇A,B的距离必须相等,到两条高速公路m和n的距离也必须相等,发射塔应修建在什么位置?请用规作图标出它的位置.
5、请仅用无刻度的直尺完成下列画图,不写画法,保留画图痕迹。
(1)如图①,四边形ABCD中,AB=AD,∠B=∠D,画出四边形ABCD的对称轴m;
如图②,四边形ABCD中,AD//BC,4∠A=∠D,画出BC边的垂直平分线n.
答案:
知识要点:
1.如果两个图形成轴对称,那么其对称轴是任何一对对应点所连线段的??垂直平分线
2.对于轴对称图形,连接任意一对对应点,作所连线段的垂直平分线??,可得到这个轴对称图形的??对称轴
易错点睛
等腰三角形的对称轴是(?D?)
A.底边上的高
B.底边上的中线
C.顶角的角平分线
D.底边的垂直平分线
【点睛】??对称轴是直线而不是线段。
典型例题:
题型一
利用基本作图解决选址问题
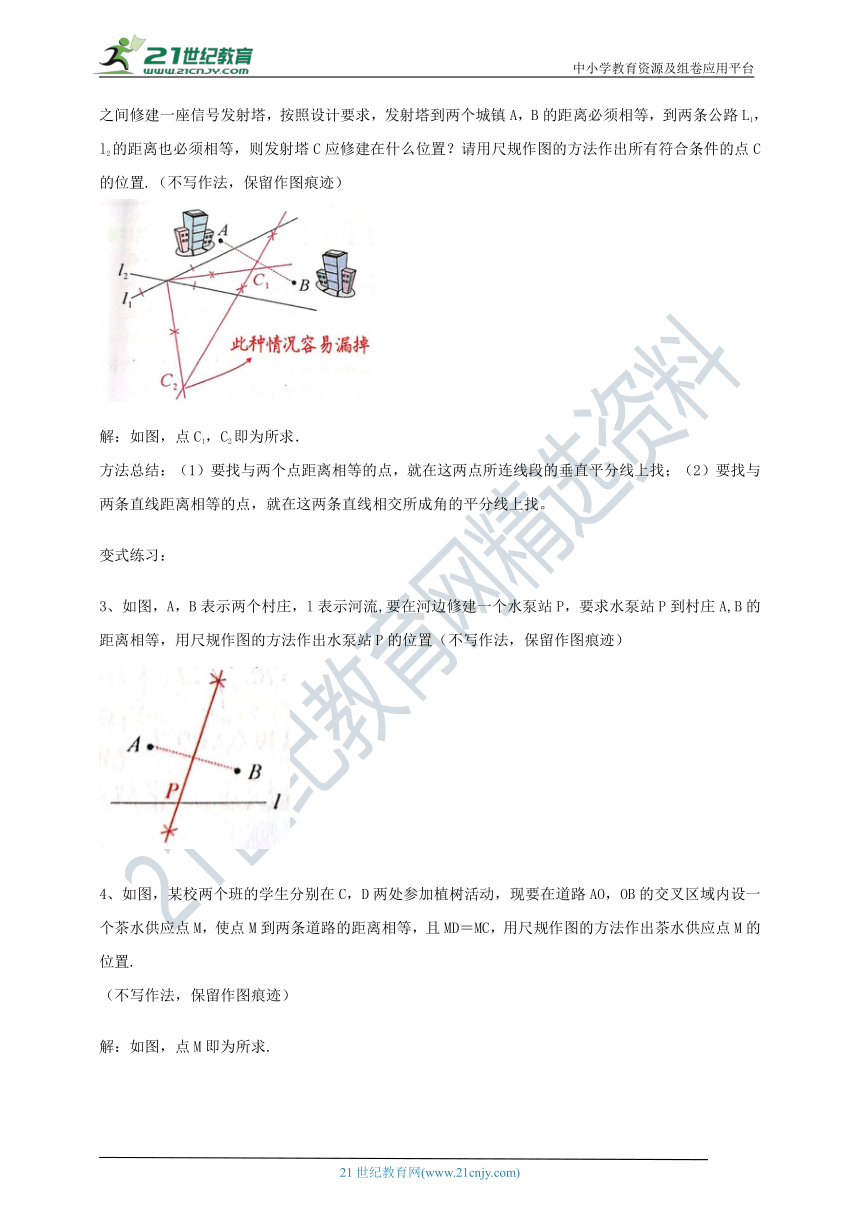
例1、「教材P66习题13.1T12变式题]如图,电信部门要在公路l2同侧、l1异侧的两个城镇A,B之间修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路L1,l2的距离也必须相等,则发射塔C应修建在什么位置?请用尺规作图的方法作出所有符合条件的点C的位置.(不写作法,保留作图痕迹)
解:如图,点C1,C2即为所求.
方法总结:(1)要找与两个点距离相等的点,就在这两点所连线段的垂直平分线上找;(2)要找与两条直线距离相等的点,就在这两条直线相交所成角的平分线上找。
变式练习:
如图,A,B表示两个村庄,l表示河流,要在河边修建一个水泵站P,要求水泵站P到村庄A,B的距离相等,用尺规作图的方法作出水泵站P的位置(不写作法,保留作图痕迹)
如图,某校两个班的学生分别在C,D两处参加植树活动,现要在道路AO,OB的交叉区域内设一个茶水供应点M,使点M到两条道路的距离相等,且MD=MC,用尺规作图的方法作出茶水供应点M的位置.
(不写作法,保留作图痕迹)
解:如图,点M即为所求.
题型二
利用基本作图进行问题探究
例2、如图,已知△ABC和ΔA'B'C'关于直线MN对称,ΔA'B'C'和ΔA"B”C”关于直线EF对称
(1)画出直线EF;(不写作法,保留作图痕迹)
(2)若直线MN与EF相交于点0,试探究∠BOB”与直线MN,EF所夹锐角<α的数量关系.
解:(1)如图,直线EF即为所求.
(2)∠BOB"=2∠α.理由如下:
∵ΔABC和ΔA'B'C'关于直线MN对称,
∴BO与B'0关于直线MN对称.
∴∠BOM=∠B'OM.
同理可得∠B'OE=∠B'OE,
∴∠BOB"=2∠B'OM+2∠B'OE=2∠MOE=2∠α.
变式练习:
如图,已知ΔABC.
(1)尺规作图:
①作线段AB的垂直平分线l;
②作射线CM平分∠ACB,与直线l交于点D,连接AD,BD.(不写作法,保留作图痕迹)
(2)在(1)的条件下,∠ACB和∠ADB的数量关系为∠ACB+∠ADB=180°?
(3)证明你所发现的(2)中的结论.
(1)解:①②如图所示.
(3)证明:如图,过点D分别作DELCA于点E,DF⊥CB的延长线于点F,则
∠DEA=∠DFB=90°.点D在AB的垂直平分线上,
∴DA=DB.
∵CD平分∠ACB,DE⊥CA,DF⊥CB,∴DE=DF.
在RtΔDAE和RtΔDBF中
DA=DB,?
DE=DF,?
∴RtΔDAE≌RtΔDBF(HL).
∴∠ADE=∠BDF.∴∠ADB=∠EDF.?
∵∠ECF+∠EDF=360°-∠CED-∠CFD=360°-?90°-90°=180°,∴∠ECF+∠ADB=180°,即?∠ACB+∠ADB=180°.?
基础练习:
作出下列轴对称图形的对称轴.
答案略
2、下列说法不正确的是(B)
A.两个关于某直线对称的图形一定全等
B.轴对称图形的对称点一定在对称轴的两侧
C.成轴对称的两个图形的对应点连线的垂直平分线是它们的对称轴
D.平面上两个全等的图形不一定关于某条直线对称
3、如图,在ΔABC中,AC<BC,用尺规作图的方法在BC上取一点P,连接PA使得PA+PC=BC,并说明理由.
解:如图,作AB的垂直平分线PD交BC于点P,
垂足为D,连接PA,
点P即为所求.理由如下:
∵PD垂直平分AB,
∴PA=PB,
∴PA+PC=PB+PC=BC.
4、【教材变式】(P66第12题改)如图,电信部门要修建一座电视信号发射塔,按照设计要求,发射塔到两个镇A,B的距离必须相等,到两条高速公路m和n的距离也必须相等,发射塔应修建在什么位置?请用规作图标出它的位置.
解:分别作∠mOn和它邻补角的平分线l1,l2,作AB的垂直平分线l3,L3与l1,l2的交点P1,P2即为发射塔的位置。
5、请仅用无刻度的直尺完成下列画图,不写画法,保留画图痕迹。
(1)如图①,四边形ABCD中,AB=AD,∠B=∠D,画出四边形ABCD的对称轴m;
如图②,四边形ABCD中,AD//BC,4∠A=∠D,画出BC边的垂直平分线n.
解:(1)如图①,直线m即为所求.
(2)如图②,直线n即为所求.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
13.1.2线段的垂直平分线的性质
第2课时
线段的垂直平分线的作法与应用
知识要点:
1.如果两个图形成轴对称,那么其对称轴是任何一对对应点所连线段的??
2.对于轴对称图形,连接任意一对对应点,作所连线段的垂直平分线??,可得到这个轴对称图形的??__________
易错点睛
等腰三角形的对称轴是(?
?)
A.底边上的高
B.底边上的中线
C.顶角的角平分线
D.底边的垂直平分线
【点睛】??对称轴是直线而不是线段。
典型例题:
题型一
利用基本作图解决选址问题
例1、「教材P66习题13.1T12变式题]如图,电信部门要在公路l2同侧、l1异侧的两个城镇A,B之间修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路L1,l2的距离也必须相等,则发射塔C应修建在什么位置?请用尺规作图的方法作出所有符合条件的点C的位置.(不写作法,保留作图痕迹)
变式练习:
如图,A,B表示两个村庄,l表示河流,要在河边修建一个水泵站P,要求水泵站P到村庄A,B的距离相等,用尺规作图的方法作出水泵站P的位置(不写作法,保留作图痕迹)
如图,某校两个班的学生分别在C,D两处参加植树活动,现要在道路AO,OB的交叉区域内设一个茶水供应点M,使点M到两条道路的距离相等,且MD=MC,用尺规作图的方法作出茶水供应点M的位置.(不写作法,保留作图痕迹)
题型二
利用基本作图进行问题探究
例2、如图,已知△ABC和ΔA'B'C'关于直线MN对称,ΔA'B'C'和ΔA"B”C”关于直线EF对称
(1)画出直线EF;(不写作法,保留作图痕迹)
(2)若直线MN与EF相交于点0,试探究∠BOB”与直线MN,EF所夹锐角<α的数量关系.
变式练习:
如图,已知ΔABC.
(1)尺规作图:
①作线段AB的垂直平分线l;
②作射线CM平分∠ACB,与直线l交于点D,连接AD,BD.(不写作法,保留作图痕迹)
(2)在(1)的条件下,∠ACB和∠ADB的数量关系为
?
(3)证明你所发现的(2)中的结论.
基础练习:
作出下列轴对称图形的对称轴.
2、下列说法不正确的是(
)
A.两个关于某直线对称的图形一定全等
B.轴对称图形的对称点一定在对称轴的两侧
C.成轴对称的两个图形的对应点连线的垂直平分线是它们的对称轴
D.平面上两个全等的图形不一定关于某条直线对称
3、如图,在ΔABC中,AC<BC,用尺规作图的方法在BC上取一点P,连接PA使得PA+PC=BC,并说明理由.
4、【教材变式】(P66第12题改)如图,电信部门要修建一座电视信号发射塔,按照设计要求,发射塔到两个镇A,B的距离必须相等,到两条高速公路m和n的距离也必须相等,发射塔应修建在什么位置?请用规作图标出它的位置.
5、请仅用无刻度的直尺完成下列画图,不写画法,保留画图痕迹。
(1)如图①,四边形ABCD中,AB=AD,∠B=∠D,画出四边形ABCD的对称轴m;
如图②,四边形ABCD中,AD//BC,4∠A=∠D,画出BC边的垂直平分线n.
答案:
知识要点:
1.如果两个图形成轴对称,那么其对称轴是任何一对对应点所连线段的??垂直平分线
2.对于轴对称图形,连接任意一对对应点,作所连线段的垂直平分线??,可得到这个轴对称图形的??对称轴
易错点睛
等腰三角形的对称轴是(?D?)
A.底边上的高
B.底边上的中线
C.顶角的角平分线
D.底边的垂直平分线
【点睛】??对称轴是直线而不是线段。
典型例题:
题型一
利用基本作图解决选址问题
例1、「教材P66习题13.1T12变式题]如图,电信部门要在公路l2同侧、l1异侧的两个城镇A,B之间修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路L1,l2的距离也必须相等,则发射塔C应修建在什么位置?请用尺规作图的方法作出所有符合条件的点C的位置.(不写作法,保留作图痕迹)
解:如图,点C1,C2即为所求.
方法总结:(1)要找与两个点距离相等的点,就在这两点所连线段的垂直平分线上找;(2)要找与两条直线距离相等的点,就在这两条直线相交所成角的平分线上找。
变式练习:
如图,A,B表示两个村庄,l表示河流,要在河边修建一个水泵站P,要求水泵站P到村庄A,B的距离相等,用尺规作图的方法作出水泵站P的位置(不写作法,保留作图痕迹)
如图,某校两个班的学生分别在C,D两处参加植树活动,现要在道路AO,OB的交叉区域内设一个茶水供应点M,使点M到两条道路的距离相等,且MD=MC,用尺规作图的方法作出茶水供应点M的位置.
(不写作法,保留作图痕迹)
解:如图,点M即为所求.
题型二
利用基本作图进行问题探究
例2、如图,已知△ABC和ΔA'B'C'关于直线MN对称,ΔA'B'C'和ΔA"B”C”关于直线EF对称
(1)画出直线EF;(不写作法,保留作图痕迹)
(2)若直线MN与EF相交于点0,试探究∠BOB”与直线MN,EF所夹锐角<α的数量关系.
解:(1)如图,直线EF即为所求.
(2)∠BOB"=2∠α.理由如下:
∵ΔABC和ΔA'B'C'关于直线MN对称,
∴BO与B'0关于直线MN对称.
∴∠BOM=∠B'OM.
同理可得∠B'OE=∠B'OE,
∴∠BOB"=2∠B'OM+2∠B'OE=2∠MOE=2∠α.
变式练习:
如图,已知ΔABC.
(1)尺规作图:
①作线段AB的垂直平分线l;
②作射线CM平分∠ACB,与直线l交于点D,连接AD,BD.(不写作法,保留作图痕迹)
(2)在(1)的条件下,∠ACB和∠ADB的数量关系为∠ACB+∠ADB=180°?
(3)证明你所发现的(2)中的结论.
(1)解:①②如图所示.
(3)证明:如图,过点D分别作DELCA于点E,DF⊥CB的延长线于点F,则
∠DEA=∠DFB=90°.点D在AB的垂直平分线上,
∴DA=DB.
∵CD平分∠ACB,DE⊥CA,DF⊥CB,∴DE=DF.
在RtΔDAE和RtΔDBF中
DA=DB,?
DE=DF,?
∴RtΔDAE≌RtΔDBF(HL).
∴∠ADE=∠BDF.∴∠ADB=∠EDF.?
∵∠ECF+∠EDF=360°-∠CED-∠CFD=360°-?90°-90°=180°,∴∠ECF+∠ADB=180°,即?∠ACB+∠ADB=180°.?
基础练习:
作出下列轴对称图形的对称轴.
答案略
2、下列说法不正确的是(B)
A.两个关于某直线对称的图形一定全等
B.轴对称图形的对称点一定在对称轴的两侧
C.成轴对称的两个图形的对应点连线的垂直平分线是它们的对称轴
D.平面上两个全等的图形不一定关于某条直线对称
3、如图,在ΔABC中,AC<BC,用尺规作图的方法在BC上取一点P,连接PA使得PA+PC=BC,并说明理由.
解:如图,作AB的垂直平分线PD交BC于点P,
垂足为D,连接PA,
点P即为所求.理由如下:
∵PD垂直平分AB,
∴PA=PB,
∴PA+PC=PB+PC=BC.
4、【教材变式】(P66第12题改)如图,电信部门要修建一座电视信号发射塔,按照设计要求,发射塔到两个镇A,B的距离必须相等,到两条高速公路m和n的距离也必须相等,发射塔应修建在什么位置?请用规作图标出它的位置.
解:分别作∠mOn和它邻补角的平分线l1,l2,作AB的垂直平分线l3,L3与l1,l2的交点P1,P2即为发射塔的位置。
5、请仅用无刻度的直尺完成下列画图,不写画法,保留画图痕迹。
(1)如图①,四边形ABCD中,AB=AD,∠B=∠D,画出四边形ABCD的对称轴m;
如图②,四边形ABCD中,AD//BC,4∠A=∠D,画出BC边的垂直平分线n.
解:(1)如图①,直线m即为所求.
(2)如图②,直线n即为所求.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
