九年级上册第四章 中心对称图形4.1圆

(共35张PPT)
苏科版 义务教育课程标准实验教科书 九年级上册
设计思路
1
2
教材分析
3
教学方法
4
教学过程
5
课后反思
设计思路
1
教师旁激侧引
学生交流探究
设计思路
1
2
教材分析
3
教学方法
4
教学过程
5
评价分析
2
教材分析
地位
本节内容是在学习
了直线型图形的有
关性质和判断的基
础上，进一步探索
一种特殊的曲线型
图形，是下面学习
圆的其它性质和知
识的基础，也学好
本章内容的关键。
作用
承上：和直线型相结
合，完善初中几何的
学习。
启下：是继续学习研
究圆的其它相关知识
的基础和关键，也是
培养学生学习思想、
学习方法的关键。
2
教材分析
知识与技能
理解圆的两个
定义；掌握点
与圆的位置关
系以及如何判
断点与圆的三
种位置关系 ，
并能应用它们
解决相关问题。
过程与方法
经历圆的定义
的形成过程 ，
在确定点和圆
的三种位置关
系的过程中体
会用数量关系
来确定位置
关系的方法 .
情感态度与价值观
通过对数学问
题和实际问题
的分析逐步学
会用归纳、转
化等方法解决
问题；让学生
体验数学价值， 感受学习数学
的乐趣。
圆
重点
与
难点
重点
圆的（描述和集
合）定义的形成
及确定点和圆的
三种位置关系.
难点
点和圆的位置关
系应用应用和点
的共圆问题 .
设计思路
1
2
教材分析
3
教学方法
4
教学过程
5
评价分析
3
教学方法
教
教师主要采用
“引导”的方
式.教师巧设
情境和活动，
以旁激侧引的
方式使学习不
断深入.
学
“自主交流探究”的方法.
学生在自主交流探究互相协作和谐发展，感受知识的生成过程.
设计思路
1
2
教材分析
3
教学方法
4
教学过程
5
评价分析
4
教学过程
情境引入
激发兴趣
操作活动
形成定义
思考探究
归纳总结
观察验证
尝试交流
探索实践
课堂回顾
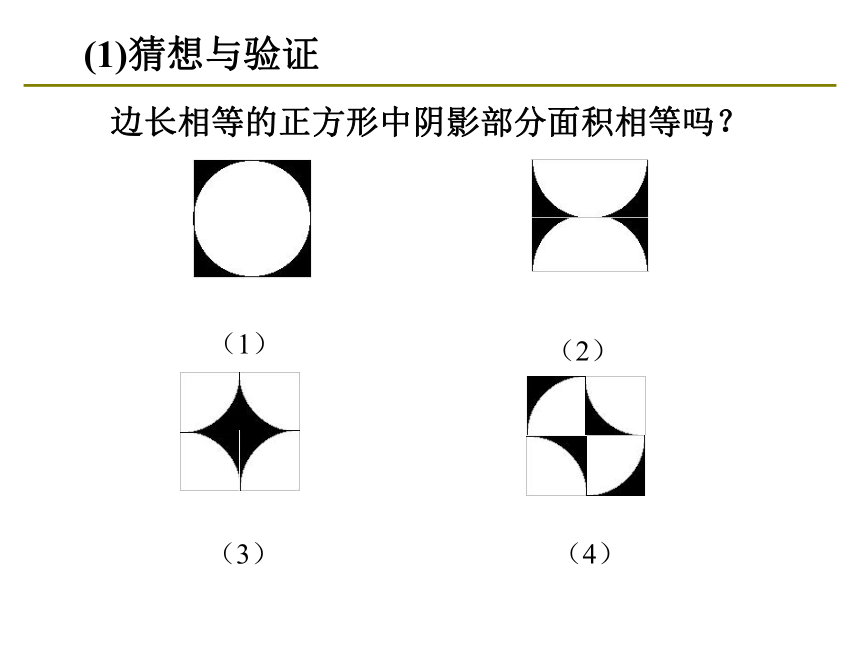
边长相等的正方形中阴影部分面积相等吗？
（1）
（2）
（3）
（4）
(1)猜想与验证
家和福到
展翅高飞
和和美美
(2)美图赏析　
圆与生活
我们怎样画圆？
操作与认识
(1)操作一：
把线段OP的端点O固定，使线段OP绕着点O在平面内旋转1 周，另一个端点P运动所形成的图形叫做圆.
定点O 叫做圆心.
线段OP叫做圆的半径.
以O为圆心的圆，记做“⊙O”，
读做“圆O”.
(2)你能用简洁的语言概括圆的定义吗
O
P
O
(1)以O为圆心画圆
(2)以AB长为半径画圆
要确定一个圆,必须确定圆的圆心和半径.
圆心确定圆的位置,半径确定圆的大小.
.
.
A
B
(3)操作二：按要求画圆.
战国时的《墨经》就有“圜，一中同长也”的记载．它的意思是:圆，只有一个圆心，从圆心到圆上各点的长都相等．
(1)思考：校运会上一名运动员在挑战校铅球13 m记录，
你知道铅球落点与该记录线有几种位置关系吗？
13 m
思考与探索
.
.
.
点在圆内
点在圆上
点在圆外
(2)探索：这个圆把平面分成了几部分？
.
O
设⊙O的半径为 r，点P到圆心的距离OP = d，那么：
·
O
r
d
P
P
P
点在圆内
点在圆上
点在圆外
d ＜ r
d ＞ r
d = r
d
d
“ ”读作“等价于”，意思是从左边能得到右边；从右边也能得
到左边。
位置和数量关系
(3)探求归纳点与圆的位置和数量关系．
　已知⊙O的直径为8 cm，判断点P与⊙O
的位置关系．
(1)若PO =4.5 cm，则点P在 ；
(2)若PO =3 cm，则点P在 ；
(3)若PO = ，则点P在圆上．
圆外
圆内
4cm
圆上各点到圆心的距离都等于半径;
到圆心距离等于半径的点都在圆上.
就是说：圆是到定点距离等于定长的点的集合.
圆外是_______________________点的集合.
圆内是_______________________点的集合.
到圆心的距离大于半径的
到圆心的距离小于半径的
圆上各点都满足什么条件？
探索与归纳
如图:已知点P、Q，且PQ=4 cm.
P
Q
(1)画出下列图形:
到点P的距离等于2 cm的点的集合;
到点Q的距离等于3 cm的点的集合.
.
.
尝试与交流
P
Q
以点P为圆心2 cm为半径的圆;
以点Q为圆心3 cm为半径的圆.
.
.
(2)在所画图中，到点P的距离等于2 cm，
且到点Q的距离等于3 cm的点的有几个？
请在图中将它们表示出来．
P
Q
A
B
.
.
.
.
(3)在所画图中，到点P 的距离小于或等于2 cm，
且到点Q 的距离大于或等于3 cm的点的集合是
怎样的图形？请把它们画出来．
P
Q
.
.
.
.
A
B
如图，BD、CE是△ABC的高，M为BC的中点.
试说明点B、C、D、E在以点M为圆心的同一个
圆上.
探索与实践
课堂小结：
(1)这节课你有哪些收获？
(2) 你还有什么疑惑吗？
(3) 通过本节课的学习我们能
感悟到：数学源于生活、寓于
生活、用于生活.
一切立体图形中最美的是球;
一切平面图形中最美的是圆.
毕达哥拉斯：
(古希腊数学家，哲学家)
http://wenwen./z/q177957631.htm
江苏省第七届园艺博览会参评会徽欣赏
作 业：
斯坦因豪斯图形
http://zhidao./question/89266534.html
2、必做题： P109 习题5.1 第1 、3题．
3、选做题： 求阴影部分的面积.
10cm
10cm
5cm
1、阅读课本：　进一步感受圆与生活息息相关,
　　　　　　 体会用数学解决问题的思想方法.
5
课后反思
1、设计上的亮点：
(1)以活动为主线，注重过程.
这节课设计了三个有主题的活动和一个猜想验证、一个探索实践，例如探索点与圆的位置及数量关系和形成圆的集合定义开展组内及小组间的研究讨论，再总结归纳结论，学生享受了知识生成过程的快感.
(2)强调学生自主探究操作，形成能力.
本节课在圆的两种定义形成时是以猜、画、量、比等操作手段为主.在上课的整个过程中，努力放给学生最大的探究空间，结合学案自主活动，从而感悟数学思想及方法，这也是遵循了课改方向，体现了课改精神.
(3)数学文化贯穿课堂始终.
以富有地方特色的剪纸文化引入课题，再引用《墨经》介绍我国悠久的数学文化，然后挖掘体育中的数学文化，最后名言赏析及给宿迁正在举行的园博会设计会徽等文化板块，既让学生得到了数学知识又了解数学文化，同时学生也会感悟到数学文化的博大精深.
2、反思之处：
(1)形成圆的集合定义时感觉设计上没能最大限度的
调动学生的参与度，感觉若能再生动直观些会更好.
(2)没能对练习题再深入挖掘.可以在练习题四点共圆
的基础上再研究矩形、菱形、等腰梯形等四边形四点
是否共圆，所好被学生以疑问的方式提出，才得以弥
补一些课堂遗憾.
5
课后反思