2021-2022学年人教版九年级上册数学21.2.4一元二次方程的根课件(45张)
文档属性
| 名称 | 2021-2022学年人教版九年级上册数学21.2.4一元二次方程的根课件(45张) |

|
|
| 格式 | zip | ||
| 文件大小 | 774.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-03 15:39:55 | ||
图片预览







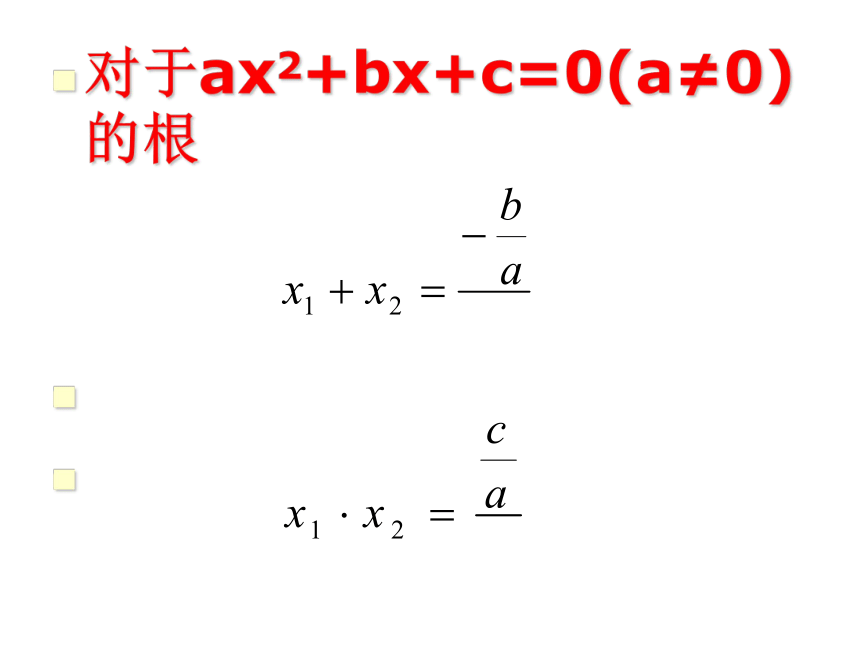


文档简介
(共45张PPT)
一元二次方程的根与系数的关系
一、回顾旧知:
1、一元二次方程的解法有哪些?
2、用公式法解一元二次方程的根是什么?
3、一元二次方程的判别式是什么?它等于什么?
一、回顾旧知:
1、一元二次方程的解法有哪些?
答:开平方法
配方法
公式法
因式分解法
2、用公式法解一元二次方程的根是什么?
3、一元二次方程的判别式是什么?它等于什么?
一、回顾旧知:
1、一元二次方程的解法有哪些?
2、用公式法解一元二次方程的根是什么?
答:
3、一元二次方程的判别式是什么?它等于什么?
,
一、回顾旧知:
1、一元二次方程的解法有哪些?
2、用公式法解一元二次方程的根是什么?
3、一元二次方程的判别式是什么?它等于什么?
答:△,
△
=b2-4ac
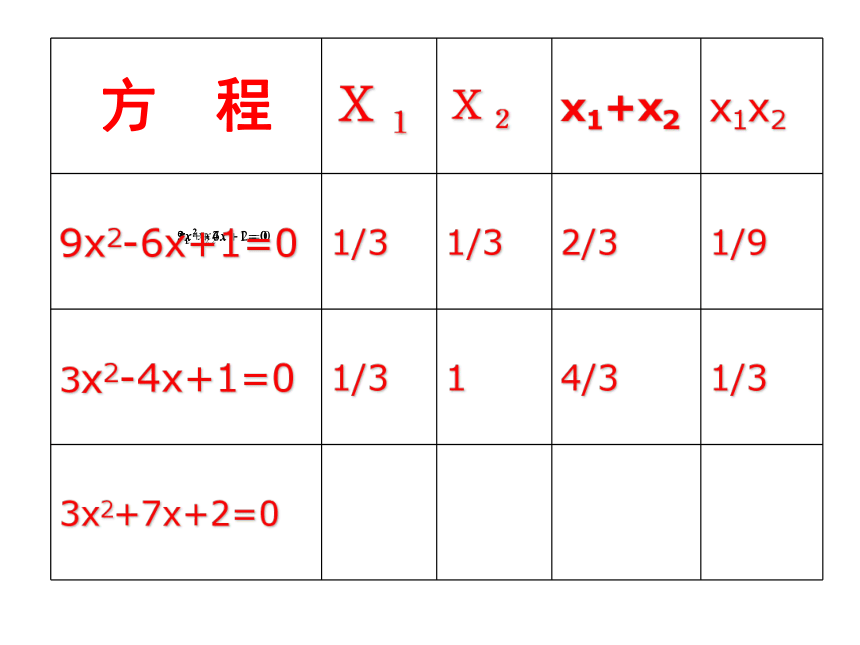
方 程
X1
X2
x1+x2
x1x2
9x2-6x+1=0
3x2-4x+1=0
3x2+7x+2=0
方 程
X1
X2
x1+x2
x1x2
9x2-6x+1=0
1/3
1/3
2/3
1/9
3x2-4x+1=0
3x2+7x+2=0
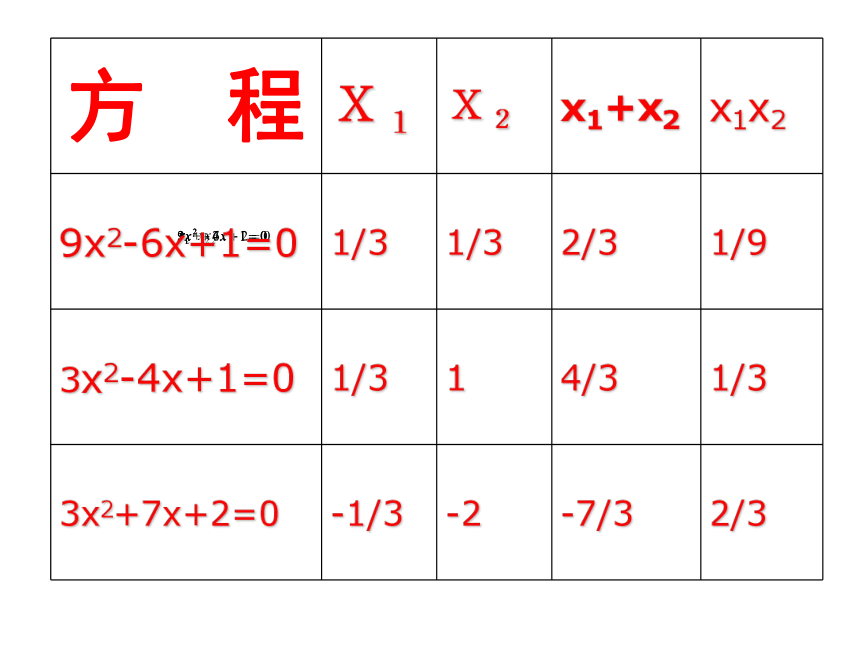
方 程
X1
X2
x1+x2
x1x2
9x2-6x+1=0
1/3
1/3
2/3
1/9
3x2-4x+1=0
1/3
1
4/3
1/3
3x2+7x+2=0
方 程
X1
X2
x1+x2
x1x2
9x2-6x+1=0
1/3
1/3
2/3
1/9
3x2-4x+1=0
1/3
1
4/3
1/3
3x2+7x+2=0
-1/3
-2
-7/3
2/3
对于ax2+bx+c=0(a≠0)的根
证
明
过
程
利用求根公式证明;
②得出结论:由此得出,一元二次方程的根与系数之间存在下列关系:
如果ax2+bx+c=0的两个根为x1、x2,那么
这个关系通常称为韦达定理。
当a=1时,方程可化为:x2+px+q=0
的形式,此时:
x1+x2=-p
x1x2=q
3、例1:下列各方程中,两根之和与两根之积各是多少?
②
③
④
因为a=2、b=-3、c=1,所以
①
②
∵a=3、b=-8、c=5
∴
③
∵a=2、b=5、c=0
∴
把方程化为一般形式:
∵a=8、b=0、c=1
∴
④
4、讲述:一元二次方程两根满足
、
,那么我们就可以利用它来判断某个数是不是一元二次方程的根:
例2:下列方程后面括号内的两个数是不是它的两个根?
①
②
解:①
∵3+4=7≠
∴
3,4不是①的根。
②
∵
∴
不是②的两根。
5、例3(P54例)已知关于x的方程
的一个根是-4,求它的另一根及k的值。
解:设方程的另一根是x2,则
解得
答:方程的另一根为
,k的值为7。
提问:能否把
代入原方程,先求出k的值,再求另一根?
解:把x=-4代入方程:
解得k=7
当k=7时,原方程为
则
练习1:下列各方程中,两根之和与两根之积各是多少?
①
(
)②
(
)
③
(
)④
(
)
⑤
(
)⑥
(
)
练习1:下列各方程中,两根之和与两根之积各是多少?
①
(3,1)②
(
)
③
(
)④
(
)
⑤
(
)⑥
(
)
练习1:下列各方程中,两根之和与两根之积各是多少?
①
(3,1)②
(
)
③
(
)④
(
)
⑤
(
)⑥
(
)
练习1:下列各方程中,两根之和与两根之积各是多少?
①
(3,1)②
(
)
③
(
)④
(
)
⑤
(
)⑥
(
)
练习1:下列各方程中,两根之和与两根之积各是多少?
①
(3,1)②
(
)
③
(
)
④
(
)
⑤
(
)⑥
(
)
练习1:下列各方程中,两根之和与两根之积各是多少?
①
(3,1)②
(
)
③
(
)④
(
)
⑤
(
0)⑥
(
)
练习1:下列各方程中,两根之和与两根之积各是多少?
①
(3,1)②
(
)
③
(
)④
(
)
⑤
(
0)⑥
(
)
练习1:下列各方程中,两根之和与两根之积各是多少?
①
(3,1)②
(
)
③
(
④
(
)
⑤
(
0)⑥
(0
)
练习2:判定下列各方程后面括号内的两个数是不是它的两个根:
①
(
)
②
(
)
③
(
)
④
(
)
⑤
(
)
练习2:判定下列各方程后面括号内的两个数是不是它的两个根:
①
(
X
)
②
(
)
③
(
)
④
(
)
⑤
(
)
练习2:判定下列各方程后面括号内的两个数是不是它的两个根:
①
(
X
)
②
(√
)
③
(
)
④
(
)
⑤
(
)
练习2:判定下列各方程后面括号内的两个数是不是它的两个根:
①
(
X
)
②
(
√
)
③
(
√
)
④
(
)
⑤
(
)
练习2:判定下列各方程后面括号内的两个数是不是它的两个根:
①
(
X
)
②
(
√
)
③
(
√
)
④
(
X
)
⑤
(
)
练习2:判定下列各方程后面括号内的两个数是不是它的两个根:
①
(
X
)
②
(
√
)
③
(
√
)
④
(
X
)
⑤
(
√
)
练习3:已知关于x的方程
的一个根是1,求它的另一个根及m的值。
解
练习4:设
是方程
的两个根,利用根与系数的关系,求下列各式的值。
①
②
四、归纳小结:
本节课学习了一元二次方程根与系数的关系,即韦达定理:
在具体的问题中希望同学们能运用韦达定理解决实际问题。
五、布置作业:
P55
习题19.4
2、3、4
谢谢!
一元二次方程的根与系数的关系
一、回顾旧知:
1、一元二次方程的解法有哪些?
2、用公式法解一元二次方程的根是什么?
3、一元二次方程的判别式是什么?它等于什么?
一、回顾旧知:
1、一元二次方程的解法有哪些?
答:开平方法
配方法
公式法
因式分解法
2、用公式法解一元二次方程的根是什么?
3、一元二次方程的判别式是什么?它等于什么?
一、回顾旧知:
1、一元二次方程的解法有哪些?
2、用公式法解一元二次方程的根是什么?
答:
3、一元二次方程的判别式是什么?它等于什么?
,
一、回顾旧知:
1、一元二次方程的解法有哪些?
2、用公式法解一元二次方程的根是什么?
3、一元二次方程的判别式是什么?它等于什么?
答:△,
△
=b2-4ac
方 程
X1
X2
x1+x2
x1x2
9x2-6x+1=0
3x2-4x+1=0
3x2+7x+2=0
方 程
X1
X2
x1+x2
x1x2
9x2-6x+1=0
1/3
1/3
2/3
1/9
3x2-4x+1=0
3x2+7x+2=0
方 程
X1
X2
x1+x2
x1x2
9x2-6x+1=0
1/3
1/3
2/3
1/9
3x2-4x+1=0
1/3
1
4/3
1/3
3x2+7x+2=0
方 程
X1
X2
x1+x2
x1x2
9x2-6x+1=0
1/3
1/3
2/3
1/9
3x2-4x+1=0
1/3
1
4/3
1/3
3x2+7x+2=0
-1/3
-2
-7/3
2/3
对于ax2+bx+c=0(a≠0)的根
证
明
过
程
利用求根公式证明;
②得出结论:由此得出,一元二次方程的根与系数之间存在下列关系:
如果ax2+bx+c=0的两个根为x1、x2,那么
这个关系通常称为韦达定理。
当a=1时,方程可化为:x2+px+q=0
的形式,此时:
x1+x2=-p
x1x2=q
3、例1:下列各方程中,两根之和与两根之积各是多少?
②
③
④
因为a=2、b=-3、c=1,所以
①
②
∵a=3、b=-8、c=5
∴
③
∵a=2、b=5、c=0
∴
把方程化为一般形式:
∵a=8、b=0、c=1
∴
④
4、讲述:一元二次方程两根满足
、
,那么我们就可以利用它来判断某个数是不是一元二次方程的根:
例2:下列方程后面括号内的两个数是不是它的两个根?
①
②
解:①
∵3+4=7≠
∴
3,4不是①的根。
②
∵
∴
不是②的两根。
5、例3(P54例)已知关于x的方程
的一个根是-4,求它的另一根及k的值。
解:设方程的另一根是x2,则
解得
答:方程的另一根为
,k的值为7。
提问:能否把
代入原方程,先求出k的值,再求另一根?
解:把x=-4代入方程:
解得k=7
当k=7时,原方程为
则
练习1:下列各方程中,两根之和与两根之积各是多少?
①
(
)②
(
)
③
(
)④
(
)
⑤
(
)⑥
(
)
练习1:下列各方程中,两根之和与两根之积各是多少?
①
(3,1)②
(
)
③
(
)④
(
)
⑤
(
)⑥
(
)
练习1:下列各方程中,两根之和与两根之积各是多少?
①
(3,1)②
(
)
③
(
)④
(
)
⑤
(
)⑥
(
)
练习1:下列各方程中,两根之和与两根之积各是多少?
①
(3,1)②
(
)
③
(
)④
(
)
⑤
(
)⑥
(
)
练习1:下列各方程中,两根之和与两根之积各是多少?
①
(3,1)②
(
)
③
(
)
④
(
)
⑤
(
)⑥
(
)
练习1:下列各方程中,两根之和与两根之积各是多少?
①
(3,1)②
(
)
③
(
)④
(
)
⑤
(
0)⑥
(
)
练习1:下列各方程中,两根之和与两根之积各是多少?
①
(3,1)②
(
)
③
(
)④
(
)
⑤
(
0)⑥
(
)
练习1:下列各方程中,两根之和与两根之积各是多少?
①
(3,1)②
(
)
③
(
④
(
)
⑤
(
0)⑥
(0
)
练习2:判定下列各方程后面括号内的两个数是不是它的两个根:
①
(
)
②
(
)
③
(
)
④
(
)
⑤
(
)
练习2:判定下列各方程后面括号内的两个数是不是它的两个根:
①
(
X
)
②
(
)
③
(
)
④
(
)
⑤
(
)
练习2:判定下列各方程后面括号内的两个数是不是它的两个根:
①
(
X
)
②
(√
)
③
(
)
④
(
)
⑤
(
)
练习2:判定下列各方程后面括号内的两个数是不是它的两个根:
①
(
X
)
②
(
√
)
③
(
√
)
④
(
)
⑤
(
)
练习2:判定下列各方程后面括号内的两个数是不是它的两个根:
①
(
X
)
②
(
√
)
③
(
√
)
④
(
X
)
⑤
(
)
练习2:判定下列各方程后面括号内的两个数是不是它的两个根:
①
(
X
)
②
(
√
)
③
(
√
)
④
(
X
)
⑤
(
√
)
练习3:已知关于x的方程
的一个根是1,求它的另一个根及m的值。
解
练习4:设
是方程
的两个根,利用根与系数的关系,求下列各式的值。
①
②
四、归纳小结:
本节课学习了一元二次方程根与系数的关系,即韦达定理:
在具体的问题中希望同学们能运用韦达定理解决实际问题。
五、布置作业:
P55
习题19.4
2、3、4
谢谢!
同课章节目录
