七年级数学镶嵌
图片预览

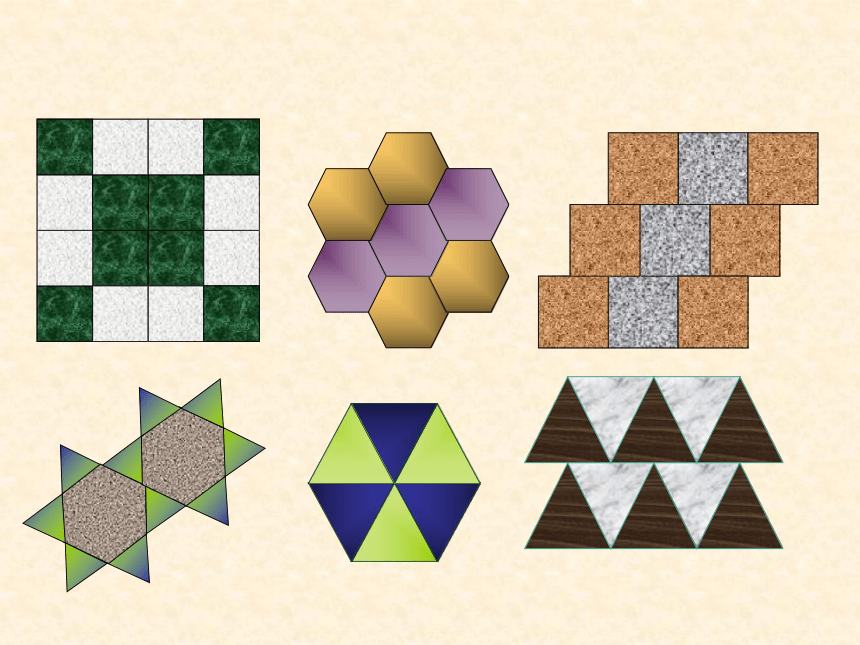


文档简介
(共37张PPT)
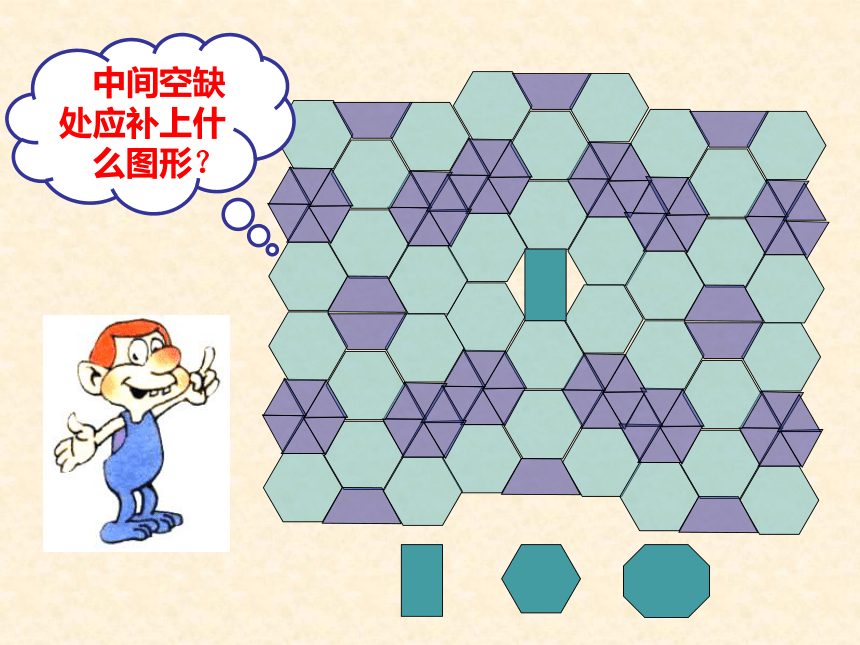
中间空缺处应补上什么图形?
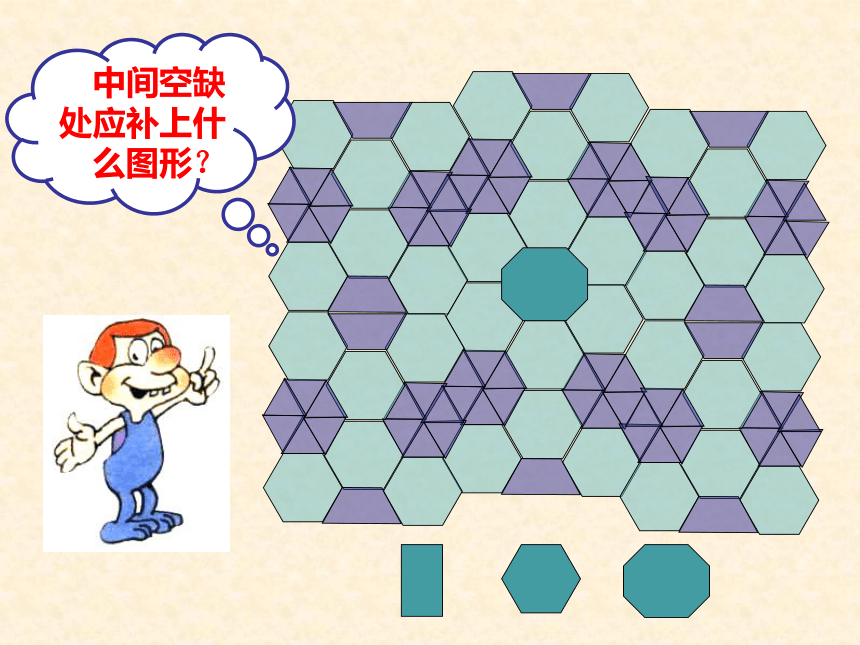
中间空缺处应补上什么图形?
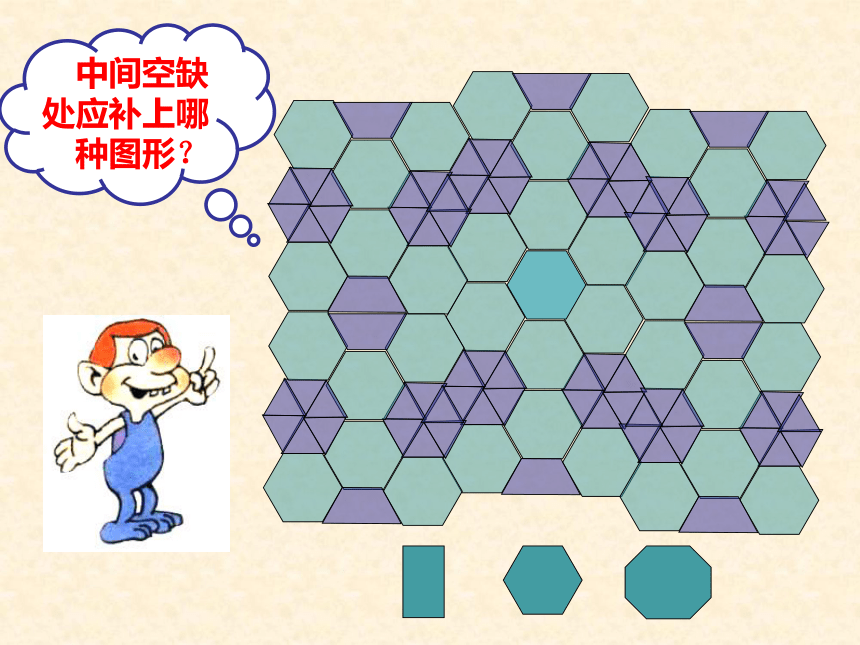
中间空缺处应补上哪种图形?
探究1:仅用一种正多边形镶嵌,哪些正多边形能单独镶嵌成一个平面图案?
60°
60°
60°
60°
60°
60°
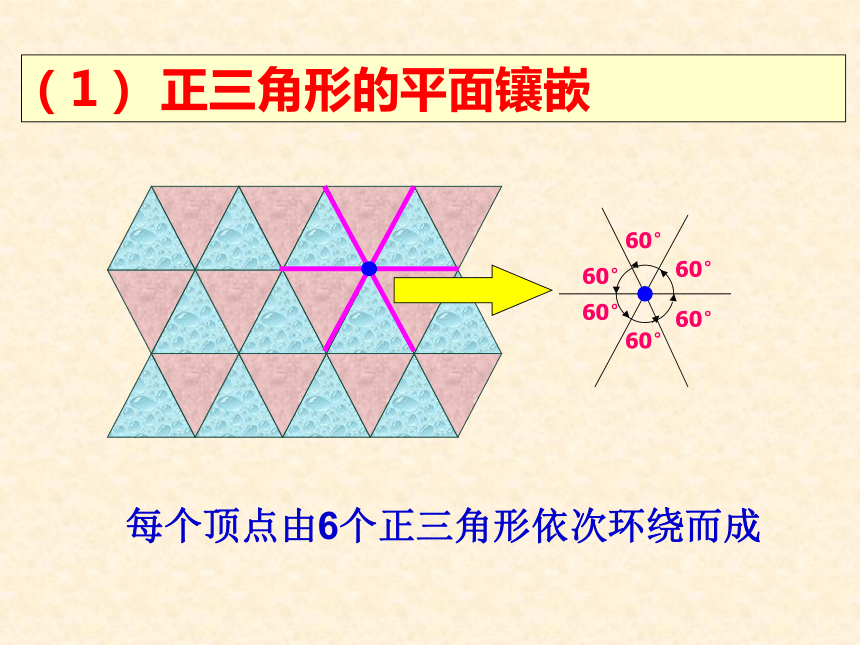
(1) 正三角形的平面镶嵌
每个顶点由6个正三角形依次环绕而成
90°
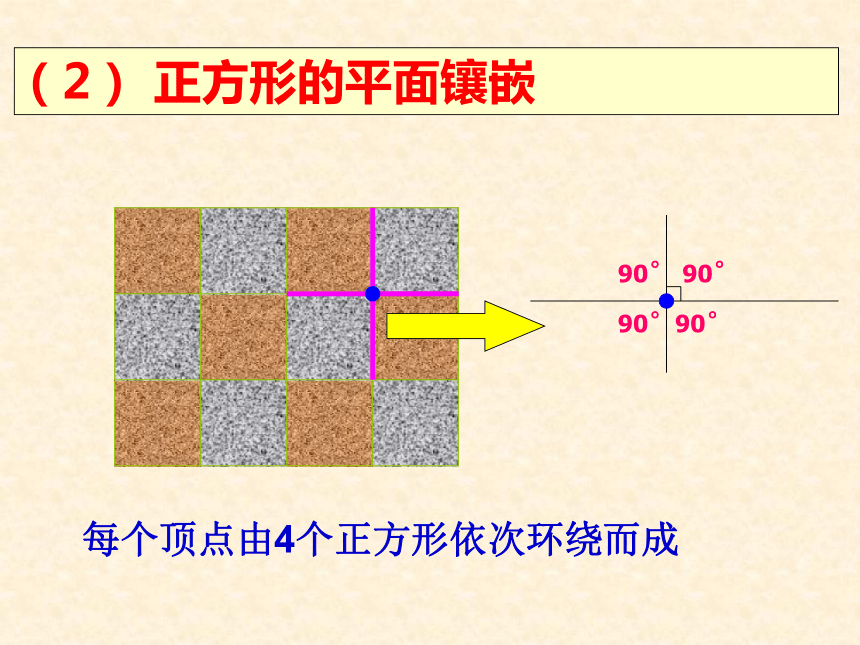
(2) 正方形的平面镶嵌
90°
90°
90°
每个顶点由4个正方形依次环绕而成
120 °
120 °
120 °
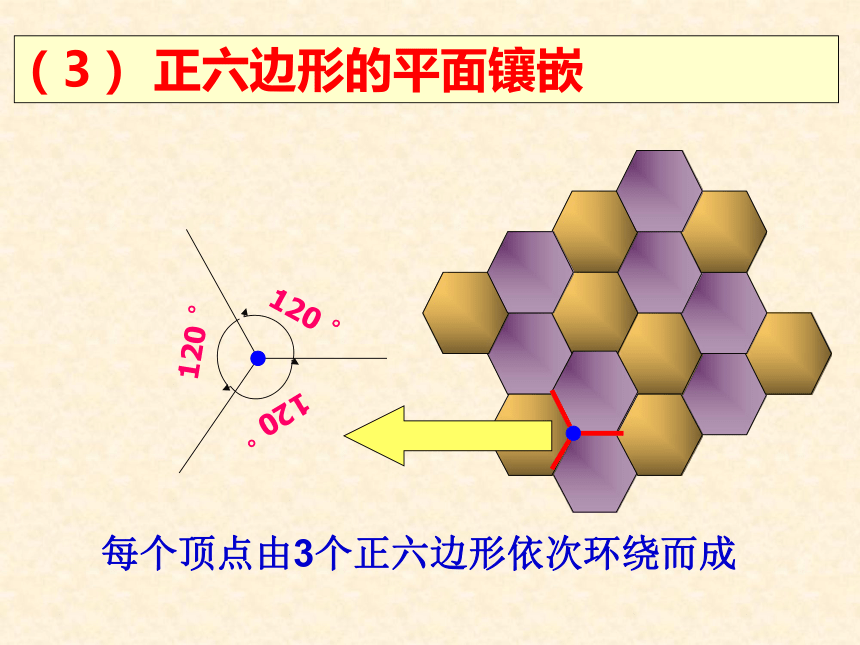
(3) 正六边形的平面镶嵌
每个顶点由3个正六边形依次环绕而成
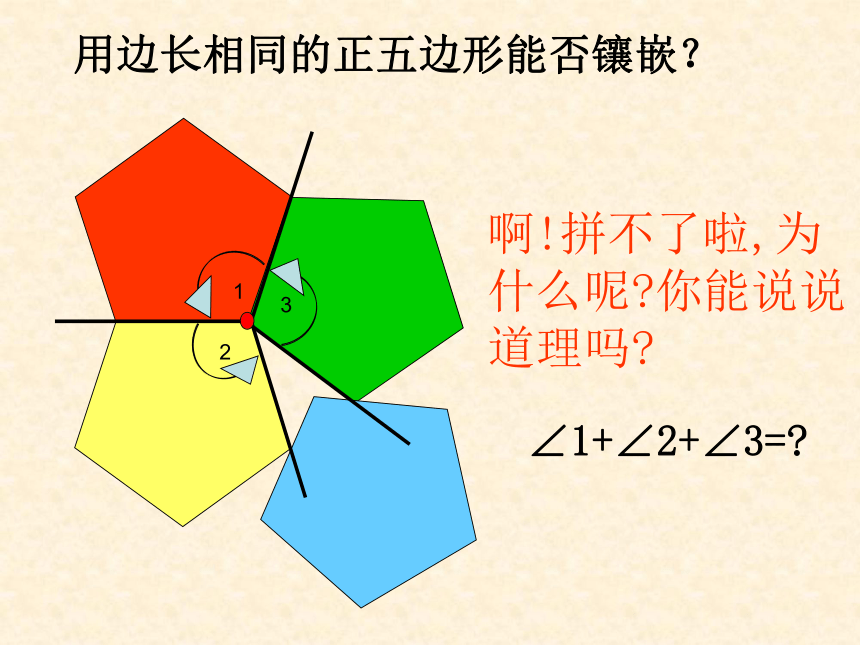
啊!拼不了啦,为什么呢 你能说说道理吗
1
2
3
∠1+∠2+∠3=
用边长相同的正五边形能否镶嵌?
多边形镶嵌的条件:
(1)拼接在同一个顶点处的各个多边形的内角之和等于360°
(2)相邻的多边形有公共边
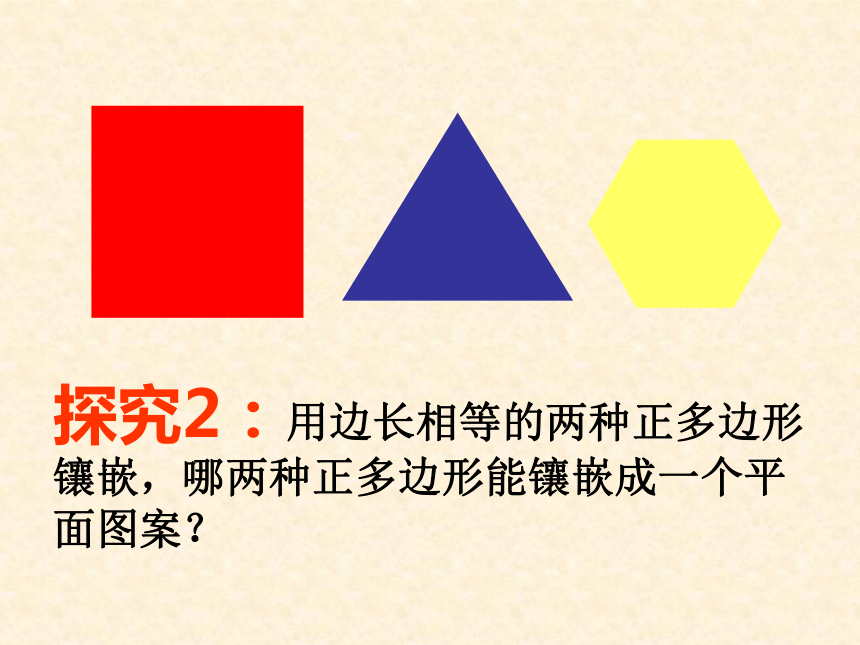
探究2:用边长相等的两种正多边形镶嵌,哪两种正多边形能镶嵌成一个平面图案?
注意:同一个组合会有不同的镶嵌效果
1、正三角形与正方形的镶嵌:
图案1
图案2
120°
120°
60°
60°
2、正三角形与正六边形的镶嵌:
图案(1)
每个顶点处各有 2个正三角形, 2个正六边形.
60°
60°
120°
60°
60°
每个顶点处各有4个正三角形, 1个正六边形
2、正三角形与正六边形的镶嵌:
图案(2)
正方形和正六边形不能镶嵌
想一想
正方形和正八边形能否镶嵌
正三角形和正十二边形能否镶嵌
135°
135°
90°
150°
150°
60°
正八边形和正方形
正十二边形和正三角形
探究3:
用几个形状、大小相同的任意三角形能镶嵌成一个平面图案吗?四边形呢?
1
3
2
1
4
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
∵ ∠1+∠2+∠3=180°
∴2(∠1+∠2+∠3)=360°
任意三角形能镶嵌成平面图案。
因为∠1+∠2+∠3+∠4=360°
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
所以任意四边形能镶嵌成平面图案。
当围绕一点拼在一起的几个正多边形的内角加在一起等于_____度时,就可进行平面镶嵌。
只用一种正多边形就可以进行平面镶嵌的正多边形只有_____ _____ _____。
练习一:
360
正三角形
正四边形
正六边形
练习二:
3.小李家装修地板,已有正三角形形状的地砖,现打算购买另一种不同形状的正多边形地砖,与正三角形地砖在同一定点处平面镶嵌,则小李不应该购买的地砖形状是( )
A.正方形
B.正六边形
C.正八边形
D.正十二边形
C
4.某人到瓷砖商店去购买一种多边形形状的瓷砖,用来铺设无缝地板,他购买的瓷砖形状不可以使( )
A.正方形
B.长方形
D.正六边形
C.正八边形
C
对自己说,你有什么收获?
对老师说,你还有什么困惑?
用三种正多边形镶嵌,哪些能镶嵌成一个平面?
课后作业:
希望同学们:
关注身边的数学
关注数学中的美
正方形、正六边形、
正十二边形的平面镶嵌
正方形、正六边形、
正十二边形的平面镶嵌
(6,4,6,12)
(4,6,4,12)
中间空缺处应补上什么图形?
中间空缺处应补上什么图形?
中间空缺处应补上哪种图形?
探究1:仅用一种正多边形镶嵌,哪些正多边形能单独镶嵌成一个平面图案?
60°
60°
60°
60°
60°
60°
(1) 正三角形的平面镶嵌
每个顶点由6个正三角形依次环绕而成
90°
(2) 正方形的平面镶嵌
90°
90°
90°
每个顶点由4个正方形依次环绕而成
120 °
120 °
120 °
(3) 正六边形的平面镶嵌
每个顶点由3个正六边形依次环绕而成
啊!拼不了啦,为什么呢 你能说说道理吗
1
2
3
∠1+∠2+∠3=
用边长相同的正五边形能否镶嵌?
多边形镶嵌的条件:
(1)拼接在同一个顶点处的各个多边形的内角之和等于360°
(2)相邻的多边形有公共边
探究2:用边长相等的两种正多边形镶嵌,哪两种正多边形能镶嵌成一个平面图案?
注意:同一个组合会有不同的镶嵌效果
1、正三角形与正方形的镶嵌:
图案1
图案2
120°
120°
60°
60°
2、正三角形与正六边形的镶嵌:
图案(1)
每个顶点处各有 2个正三角形, 2个正六边形.
60°
60°
120°
60°
60°
每个顶点处各有4个正三角形, 1个正六边形
2、正三角形与正六边形的镶嵌:
图案(2)
正方形和正六边形不能镶嵌
想一想
正方形和正八边形能否镶嵌
正三角形和正十二边形能否镶嵌
135°
135°
90°
150°
150°
60°
正八边形和正方形
正十二边形和正三角形
探究3:
用几个形状、大小相同的任意三角形能镶嵌成一个平面图案吗?四边形呢?
1
3
2
1
4
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
∵ ∠1+∠2+∠3=180°
∴2(∠1+∠2+∠3)=360°
任意三角形能镶嵌成平面图案。
因为∠1+∠2+∠3+∠4=360°
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
所以任意四边形能镶嵌成平面图案。
当围绕一点拼在一起的几个正多边形的内角加在一起等于_____度时,就可进行平面镶嵌。
只用一种正多边形就可以进行平面镶嵌的正多边形只有_____ _____ _____。
练习一:
360
正三角形
正四边形
正六边形
练习二:
3.小李家装修地板,已有正三角形形状的地砖,现打算购买另一种不同形状的正多边形地砖,与正三角形地砖在同一定点处平面镶嵌,则小李不应该购买的地砖形状是( )
A.正方形
B.正六边形
C.正八边形
D.正十二边形
C
4.某人到瓷砖商店去购买一种多边形形状的瓷砖,用来铺设无缝地板,他购买的瓷砖形状不可以使( )
A.正方形
B.长方形
D.正六边形
C.正八边形
C
对自己说,你有什么收获?
对老师说,你还有什么困惑?
用三种正多边形镶嵌,哪些能镶嵌成一个平面?
课后作业:
希望同学们:
关注身边的数学
关注数学中的美
正方形、正六边形、
正十二边形的平面镶嵌
正方形、正六边形、
正十二边形的平面镶嵌
(6,4,6,12)
(4,6,4,12)
