八年级数学勾股定理的逆定理
图片预览







文档简介
(共25张PPT)
回顾直角三角形的性质
(1)有一个角是直角;
(2)两个锐角互余 ;
(3)两直角边的平方和等于斜边的平方 ;
(4)在直角三角形中, 如果有一个锐角是30°,那么它
所对的直角边是斜边的一半 ;
(5)在直角三角形中, 如果一条直角边是斜边的一半,
那么它所对的锐角是30°;
反之,一个三角形满足什么条件,才能是直角三角形呢
思考:
(1)有一个角是直角的三角形是直角三角形;
(2)有两个角的和是90°的三角形是直角三角形;
(3)如果一个三角形的三边a ,b ,c 满足a2 +b 2=c2 ,
那么这个三角形是直角三角形
一个三角形满足什么条件才能是直角三角形
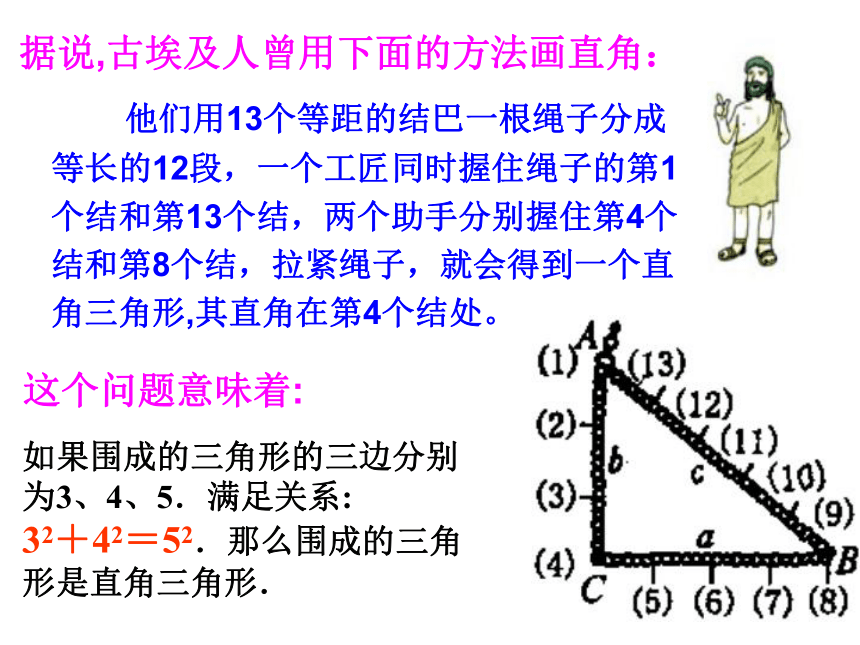
据说,古埃及人曾用下面的方法画直角:
他们用13个等距的结巴一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其直角在第4个结处。
这个问题意味着:
如果围成的三角形的三边分别为3、4、5.满足关系: 32+42=52.那么围成的三角形是直角三角形.
勾股定理:如果直角三角形两直角边分别为a,b,斜边为c,那么 。
a2 + b2 = c2
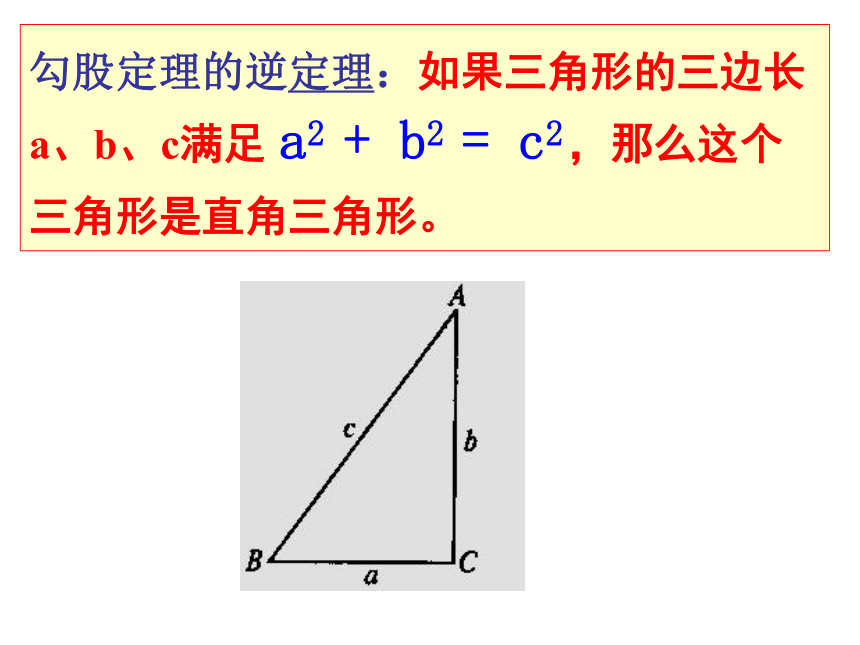
逆命题:如果三角形的三边长a、b、c满足 ,那么这个三角形是直角三角形。
a2 + b2 = c2
互逆命题
逆命题:如果三角形的三边长a、b、c满足 ,那么这个三角形是直角三角形。
a2 + b2 = c2
已知△ABC,AB=c,AC=b,BC=a,且a2+b2=c2,
求证:∠C=900
证明:作RT△A′B′C′,
使∠C′=900,A′C′=b,B′C′=a
则△ABC≌ △A′B′C′
∴∠C=900
勾股定理的逆定理:如果三角形的三边长a、b、c满足 ,那么这个三角形是直角三角形。
a2 + b2 = c2
分析:根据勾股定理的逆定理, 判断一个三角形是不是直角三角形, 只要看两条较少边长的平方和是否等于最大边长的平方.
例1:判断由线段a,b,c组成的三角形是不是直角
三角形
(1) a=15,b=17,c=8; (2) a=13,b=15,c=14
解:(1)最大边为17
∵152+82=225+64 =289
172 =289
∴152+82 =172
∴以15, 8, 17为边长的三角形是直角三角形
(2)最大边为15
∵132+142=169+196=365
152 =225
∴132+ 142 ≠ 152
∴以13, 15, 14为边长的三角形不是直角三角形
像15,17,8,能够成为直角三角形三条边长的三个正整数,称为勾股数.
下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?
(1) a=25 b=20 c=15 ____ _____ ;
(2) a=13 b=14 c=15 ____ _____ ;
(4) a:b: c=3:4:5 _____ _____ ;
是
是
不是
是
∠ A=900
∠ B=900
∠ C=900
(3) a=1 b=2 c= ____ _____ ;
(1)两条直线平行,内错角相等.
(2)如果两个实数相等,那么它们的立方相等.
(3)如果两个实数相等,那么它们的绝对值相等.
(4)全等三角形的对应角相等.
(5)对顶角相等
练:说出下列命题的逆命题.这些命题的逆命题成立吗
逆命题: 内错角相等,两条直线平行. 成立
逆命题:如果两个实数的立方相等,那么这两个实数相等. 成立
逆命题:如果两个实数的绝对值相等,那么这两个实数相等. 不成立
逆命题:对应角相等的两个三角形是全等三角形. 不成立
逆命题:相等的两个角是对顶角. 不成立
感悟: 原命题成立时, 逆命题有时成立, 有时不成立
练习3:
1、小蒋要求△ABC的的最长边上的高,测得AB=8cm,
AC=6cm,BC=10cm。则可知最长边上的高_______
4.8cm
2. 满足下列条件的△ABC,不是直角三角形的是( )
A.b2=a2-c2 B. a:b:c=3:4:5
C.∠C=∠A-∠B D. ∠A:∠B : ∠C =3:4:5
D
3.在下列长度的各组线段中,能组成直角三角形的是( )
A. 5,6,7 B. 32,42,52 C. 5,11,12 D. 5,12,13
D
4.若一个三角形的三边长分别为: 32, 42, x2 ,则此三角形是
直角三角形的x2的值是_____________
5.求证:m2-n2,m2+n2,2mn(m>n,m,n是正整数)是直角三角形的三条边长。
B
A、锐角三角形 B、直角三角形C、钝角三角形 D、等边三角形
△ABC三边a,b,c为边向外作正方形,正三角形,以三边为直径作半圆,若S1+S2=S3成立,则
是直角三角形吗?
A
C
a
b
c
S1
S2
S3
B
A
B
C
a
b
c
S1
S2
S3
已知:如图,四边形ABCD中,∠B=900,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积
A
B
C
D
中考链接
S四边形ABCD=36
一个零件的形状如下图所示,按规定这个零件
中∠A和∠DBC都应为直角.工人师傅量出了这个
零件各边尺寸,那么这个零件符合要求吗
此时四边形ABCD
的面积是多少
6. 已知a,b,c为△ABC的三边,且 满足
a2+b2+c2+338=10a+24b+26c.
试判断△ABC的形状.
已知:如图,四边形ABCD中,AB=20,BC=15,
CD=7,AD=24, ∠B=90°
求证:∠A+∠C=180°
A
B
C
D
20
15
7
24
如图BE⊥AE, ∠A=∠EBC=60°,AB=4,BC=
CD= DE=3,求证:AD⊥CD
A
B
C
D
4
E
3
60°
60°
思考题
“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里。它们离开港口一个半小时后相距30海里。如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
E
N
R
Q
S
P
解:根据题意画图,如图所示:
PQ=16×1.5=24
PR=12×1.5=18
QR=30
∵242+182=302,
即 PQ2+PR2=QR2
∴∠QPR=900
由”远航“号沿东北方向航行可知,∠QPS=450.所以∠RPS=450,
即“海天”号沿西北方向航行.
R’
或东南方向
分析:先来判断a,b,c三边哪条最长,可以代m,n为满足条件的特殊值来试,m=5,n=4.则a=9,b=40,c=41,c最大。
∴△ABC是直角三角形
7. 阅读下列解题过程: 已知a,b,c为△ABC的三边,且
满足a2c2-b2c2=a4-b4, 试判断△ABC的形状.
解∵ a2c2-b2c2=a4-b4 ①
∴ (a2-b2)c2=(a2+b2)(a2-b2) ②
∴ c2=a2+b2 ③
∴ △ABC是直角三角形
问:上述解题过程,从哪一步开始出现错误 请写出该步的序号:______,错误的原因为:______________;本题正确的结论
是______________________
③
a2-b2可能为0
直角三角形或等腰三角形
8.已知:在△ABC中,AB=13cm,BC=10cm,
BC边上的中线AD=12cm.
求证:AB=AC.
活动与探究
给出一组式子:32+42=52,82+62=102,
152+82=172,242+102=262.…
(1)你能发现上面式子的规律吗 请你用发现的规律,给
出第5个式子;
(2)请你证明你所发现的规律.
9.已知:在△ABC中,AB=AC=26, 点D是AC上一点,
CD=2,BD=10.
求: △ABC的面积 .
在RtΔABC中,AC=BC,点PA是三角形内一点,PA=3,PB=1,PC=2,
求证:∠BPC=135°
A
B
C
P
P’
(A)
在一根长为180个单位的绳子上,分别标出A,B,C,D四个点,它们将绳子分为长为60个单位、45个单位和75个单位的三段线段。
自己握住绳子的两个端点(A点和D点),两名同伴分别握住B点和C点,一起将绳子拉直,会得到一根什么形状?为什么?
自主评价:
1、勾股定理的逆定理
2、什么叫做互逆命题、原命题与逆命题
3、什么称为互为逆定理。
回顾直角三角形的性质
(1)有一个角是直角;
(2)两个锐角互余 ;
(3)两直角边的平方和等于斜边的平方 ;
(4)在直角三角形中, 如果有一个锐角是30°,那么它
所对的直角边是斜边的一半 ;
(5)在直角三角形中, 如果一条直角边是斜边的一半,
那么它所对的锐角是30°;
反之,一个三角形满足什么条件,才能是直角三角形呢
思考:
(1)有一个角是直角的三角形是直角三角形;
(2)有两个角的和是90°的三角形是直角三角形;
(3)如果一个三角形的三边a ,b ,c 满足a2 +b 2=c2 ,
那么这个三角形是直角三角形
一个三角形满足什么条件才能是直角三角形
据说,古埃及人曾用下面的方法画直角:
他们用13个等距的结巴一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其直角在第4个结处。
这个问题意味着:
如果围成的三角形的三边分别为3、4、5.满足关系: 32+42=52.那么围成的三角形是直角三角形.
勾股定理:如果直角三角形两直角边分别为a,b,斜边为c,那么 。
a2 + b2 = c2
逆命题:如果三角形的三边长a、b、c满足 ,那么这个三角形是直角三角形。
a2 + b2 = c2
互逆命题
逆命题:如果三角形的三边长a、b、c满足 ,那么这个三角形是直角三角形。
a2 + b2 = c2
已知△ABC,AB=c,AC=b,BC=a,且a2+b2=c2,
求证:∠C=900
证明:作RT△A′B′C′,
使∠C′=900,A′C′=b,B′C′=a
则△ABC≌ △A′B′C′
∴∠C=900
勾股定理的逆定理:如果三角形的三边长a、b、c满足 ,那么这个三角形是直角三角形。
a2 + b2 = c2
分析:根据勾股定理的逆定理, 判断一个三角形是不是直角三角形, 只要看两条较少边长的平方和是否等于最大边长的平方.
例1:判断由线段a,b,c组成的三角形是不是直角
三角形
(1) a=15,b=17,c=8; (2) a=13,b=15,c=14
解:(1)最大边为17
∵152+82=225+64 =289
172 =289
∴152+82 =172
∴以15, 8, 17为边长的三角形是直角三角形
(2)最大边为15
∵132+142=169+196=365
152 =225
∴132+ 142 ≠ 152
∴以13, 15, 14为边长的三角形不是直角三角形
像15,17,8,能够成为直角三角形三条边长的三个正整数,称为勾股数.
下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?
(1) a=25 b=20 c=15 ____ _____ ;
(2) a=13 b=14 c=15 ____ _____ ;
(4) a:b: c=3:4:5 _____ _____ ;
是
是
不是
是
∠ A=900
∠ B=900
∠ C=900
(3) a=1 b=2 c= ____ _____ ;
(1)两条直线平行,内错角相等.
(2)如果两个实数相等,那么它们的立方相等.
(3)如果两个实数相等,那么它们的绝对值相等.
(4)全等三角形的对应角相等.
(5)对顶角相等
练:说出下列命题的逆命题.这些命题的逆命题成立吗
逆命题: 内错角相等,两条直线平行. 成立
逆命题:如果两个实数的立方相等,那么这两个实数相等. 成立
逆命题:如果两个实数的绝对值相等,那么这两个实数相等. 不成立
逆命题:对应角相等的两个三角形是全等三角形. 不成立
逆命题:相等的两个角是对顶角. 不成立
感悟: 原命题成立时, 逆命题有时成立, 有时不成立
练习3:
1、小蒋要求△ABC的的最长边上的高,测得AB=8cm,
AC=6cm,BC=10cm。则可知最长边上的高_______
4.8cm
2. 满足下列条件的△ABC,不是直角三角形的是( )
A.b2=a2-c2 B. a:b:c=3:4:5
C.∠C=∠A-∠B D. ∠A:∠B : ∠C =3:4:5
D
3.在下列长度的各组线段中,能组成直角三角形的是( )
A. 5,6,7 B. 32,42,52 C. 5,11,12 D. 5,12,13
D
4.若一个三角形的三边长分别为: 32, 42, x2 ,则此三角形是
直角三角形的x2的值是_____________
5.求证:m2-n2,m2+n2,2mn(m>n,m,n是正整数)是直角三角形的三条边长。
B
A、锐角三角形 B、直角三角形C、钝角三角形 D、等边三角形
△ABC三边a,b,c为边向外作正方形,正三角形,以三边为直径作半圆,若S1+S2=S3成立,则
是直角三角形吗?
A
C
a
b
c
S1
S2
S3
B
A
B
C
a
b
c
S1
S2
S3
已知:如图,四边形ABCD中,∠B=900,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积
A
B
C
D
中考链接
S四边形ABCD=36
一个零件的形状如下图所示,按规定这个零件
中∠A和∠DBC都应为直角.工人师傅量出了这个
零件各边尺寸,那么这个零件符合要求吗
此时四边形ABCD
的面积是多少
6. 已知a,b,c为△ABC的三边,且 满足
a2+b2+c2+338=10a+24b+26c.
试判断△ABC的形状.
已知:如图,四边形ABCD中,AB=20,BC=15,
CD=7,AD=24, ∠B=90°
求证:∠A+∠C=180°
A
B
C
D
20
15
7
24
如图BE⊥AE, ∠A=∠EBC=60°,AB=4,BC=
CD= DE=3,求证:AD⊥CD
A
B
C
D
4
E
3
60°
60°
思考题
“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里。它们离开港口一个半小时后相距30海里。如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
E
N
R
Q
S
P
解:根据题意画图,如图所示:
PQ=16×1.5=24
PR=12×1.5=18
QR=30
∵242+182=302,
即 PQ2+PR2=QR2
∴∠QPR=900
由”远航“号沿东北方向航行可知,∠QPS=450.所以∠RPS=450,
即“海天”号沿西北方向航行.
R’
或东南方向
分析:先来判断a,b,c三边哪条最长,可以代m,n为满足条件的特殊值来试,m=5,n=4.则a=9,b=40,c=41,c最大。
∴△ABC是直角三角形
7. 阅读下列解题过程: 已知a,b,c为△ABC的三边,且
满足a2c2-b2c2=a4-b4, 试判断△ABC的形状.
解∵ a2c2-b2c2=a4-b4 ①
∴ (a2-b2)c2=(a2+b2)(a2-b2) ②
∴ c2=a2+b2 ③
∴ △ABC是直角三角形
问:上述解题过程,从哪一步开始出现错误 请写出该步的序号:______,错误的原因为:______________;本题正确的结论
是______________________
③
a2-b2可能为0
直角三角形或等腰三角形
8.已知:在△ABC中,AB=13cm,BC=10cm,
BC边上的中线AD=12cm.
求证:AB=AC.
活动与探究
给出一组式子:32+42=52,82+62=102,
152+82=172,242+102=262.…
(1)你能发现上面式子的规律吗 请你用发现的规律,给
出第5个式子;
(2)请你证明你所发现的规律.
9.已知:在△ABC中,AB=AC=26, 点D是AC上一点,
CD=2,BD=10.
求: △ABC的面积 .
在RtΔABC中,AC=BC,点PA是三角形内一点,PA=3,PB=1,PC=2,
求证:∠BPC=135°
A
B
C
P
P’
(A)
在一根长为180个单位的绳子上,分别标出A,B,C,D四个点,它们将绳子分为长为60个单位、45个单位和75个单位的三段线段。
自己握住绳子的两个端点(A点和D点),两名同伴分别握住B点和C点,一起将绳子拉直,会得到一根什么形状?为什么?
自主评价:
1、勾股定理的逆定理
2、什么叫做互逆命题、原命题与逆命题
3、什么称为互为逆定理。
