陕西省汉中市汉台县高中2022届高三上学期月考(一)文科数学试题(Word版,含答案)
文档属性
| 名称 | 陕西省汉中市汉台县高中2022届高三上学期月考(一)文科数学试题(Word版,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 470.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-03 07:45:27 | ||
图片预览


文档简介
汉台高中2022届高三第一次月考文科数学试卷
2021.8.28
第Ⅰ卷(选择题)
一、单选题(共60分)
1.
已知集合,,则(
)
A.
B.
C.
D.
2.
命题:,,命题:,,则下列命题中是真命题的是(
)
A.
B.
C.
D.
3.
函数的单调递增区间是(
)
A.
B.
C.
D.
4.
函数是定义在上的偶函数,在上是减函数且,则使的的取值范围(
)
A.
B.
C.
D.
5.
已知是定义域为的奇函数,满足,若,则(
)
A.
50
B.
2
C.
0
D.
-50
6.
若偶函数满足,,则(
)
A.
2
B.
-2
C.
1
D.
-1
7.
已知函数的图象关于直线对称,则函数的值域为(
)
A.
B.
C.
D.
8.
函数的图像的切线斜率可能为(
)
A.
B.
-2
C.
D.
-4
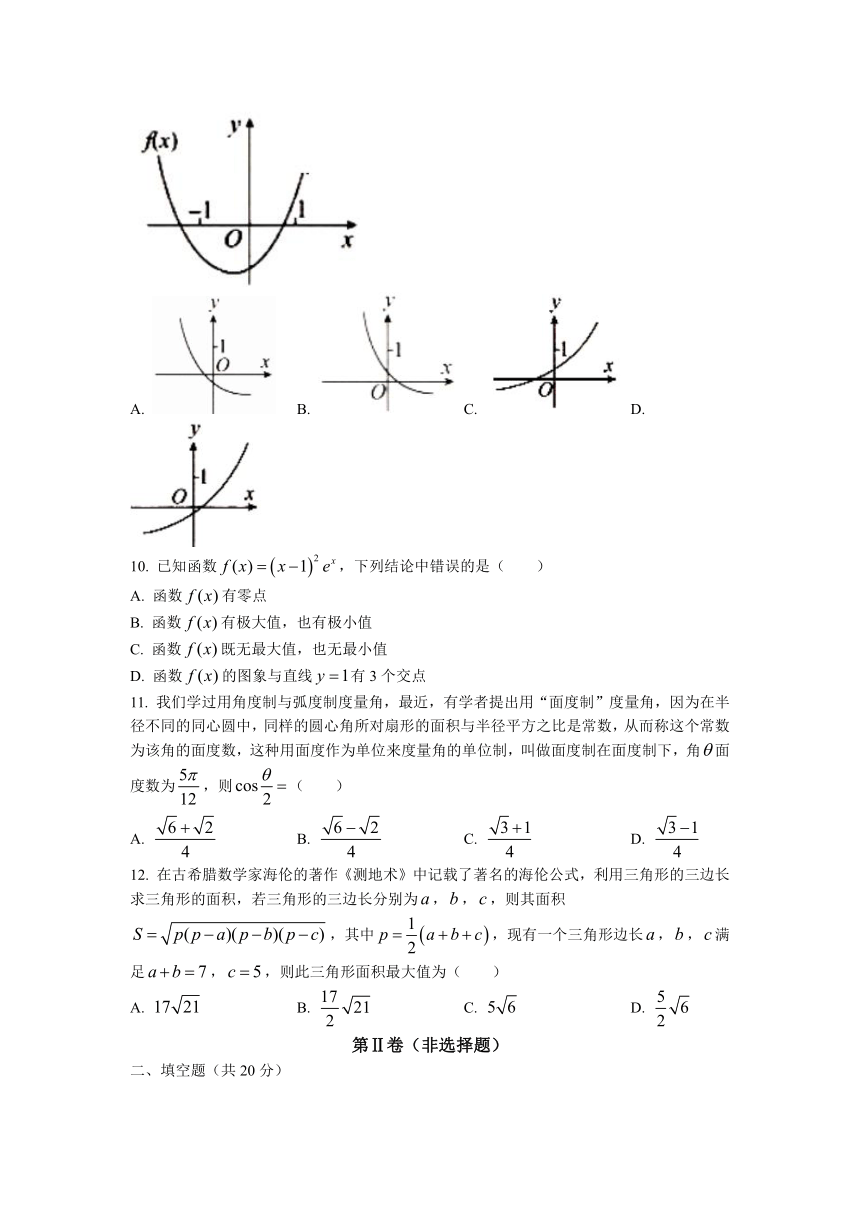
9.
已知函数(其中)的图象如图所示,则函数的图像是(
)
A.
B.
C.
D.
10.
已知函数,下列结论中错误的是(
)
A.
函数有零点
B.
函数有极大值,也有极小值
C.
函数既无最大值,也无最小值
D.
函数的图象与直线有3个交点
11.
我们学过用角度制与弧度制度量角,最近,有学者提出用“面度制”度量角,因为在半径不同的同心圆中,同样的圆心角所对扇形的面积与半径平方之比是常数,从而称这个常数为该角的面度数,这种用面度作为单位来度量角的单位制,叫做面度制在面度制下,角面度数为,则(
)
A.
B.
C.
D.
12.
在古希腊数学家海伦的著作《测地术》中记载了著名的海伦公式,利用三角形的三边长求三角形的面积,若三角形的三边长分别为,,,则其面积,其中,现有一个三角形边长,,满足,,则此三角形面积最大值为(
)
A.
B.
C.
D.
第Ⅱ卷(非选择题)
二、填空题(共20分)
13.
已知函数在区间上有最大值6,最小值5,则实数的取值范围是__________.
14.
函数是幂函数且为偶函数,则的值为___________.
15.
已知函数,若,则__________.
16.
下列说法正确的序号是:__________.
①偶函数的定义域为,则;
②一次函数满足,则函数的解析式为;
③奇函数在上单调递增,且最大值为8,最小值为-1,则;
④若集合中至多有一个元素,则.
三、解答题(共70分)
17.
已知全集,集合,集合.
(1)若,求,;
(2)若,求实数的取值范围.
18.
已知函数,并且的解集也是不等式解集.
(1)求的解析式;
(2)若在区间上不单调,求实数的取值范围.
19.
已知,,,.
(1)求的值;
(2)求的值.
20.
已知函数,在一周期内,当时,取得最大值3,当时,取得最小值-3,求:
(1)函数的解析式;
(2)求出函数的单调递增区间、对称轴方程、对称中心坐标;
(3)当时,求函数的值域.
21.
已知锐角内角,,及对边,,,满足.
(1)求的大小;
(2)若,求的取值范围.
22.
已知函数为,其中为常数.
(1)当时,求的最大值;
(2)若在区间(为自然对数的底数)上的最大值为-3,求的值.
汉台高中2022届高三第一次月考文科数学参考答案
一、选择题:
1-5:ADDCB
6-10:DBAAC
11-12:BD
二、填空题:
13.
14.
-1
15.
-3
16.
①③
三、解答题:
17.【详解】(1)由题意,
当时,,则,
所以,;
(2)若,则,
∴,解得,∴实数的取值范围是.
18.【详解】(1)不等式的解集为,
依题意,方程的两个根为-3和2,则,
由根与系数关系可得:,解得,
所以的解析式为;
(2)由(1)可知函数的图象的对称轴为,
若在区间上不单调,则有,解得,
所以实数的取值范围是.
19.【详解】(1)∵,
;
(2)由,可得,,
则;
,
则
.
20.【详解】(1)由题设知,,周期,,由得.
所以.
又因为时,取得最大值3,
即,∴,解得,又,
所以,所以.
(2)由,得,
所以函数的单调递增区间为.
由,,得,.
对称轴方程为,.
由,得.
所以,该函数的对称中心为.
(3)因为,所以,则,
所以,所以值域为:.
所以函数的值域为.
21.【详解】(1)因为,
由正弦定理可得,
又因为,
所以,
可得,由,可得.
(2)因为,,
由正弦定理,可得,,
可得,
因为锐角三角形中,所以,解得,所以,
所以,可得.
22.【详解】(1)∵,∴.
当时,,.
当时,;当时,.
∴在上是增函数,在上是减函数,.
(2)∵,,∴.
①若,则,在上是增函数,
∴.不合题意.
②若,则由,即,
由,即.
从而在上为增函数,在上为减函数,
∴.
令,则,∴,即.
∵,∴为所求.
2021.8.28
第Ⅰ卷(选择题)
一、单选题(共60分)
1.
已知集合,,则(
)
A.
B.
C.
D.
2.
命题:,,命题:,,则下列命题中是真命题的是(
)
A.
B.
C.
D.
3.
函数的单调递增区间是(
)
A.
B.
C.
D.
4.
函数是定义在上的偶函数,在上是减函数且,则使的的取值范围(
)
A.
B.
C.
D.
5.
已知是定义域为的奇函数,满足,若,则(
)
A.
50
B.
2
C.
0
D.
-50
6.
若偶函数满足,,则(
)
A.
2
B.
-2
C.
1
D.
-1
7.
已知函数的图象关于直线对称,则函数的值域为(
)
A.
B.
C.
D.
8.
函数的图像的切线斜率可能为(
)
A.
B.
-2
C.
D.
-4
9.
已知函数(其中)的图象如图所示,则函数的图像是(
)
A.
B.
C.
D.
10.
已知函数,下列结论中错误的是(
)
A.
函数有零点
B.
函数有极大值,也有极小值
C.
函数既无最大值,也无最小值
D.
函数的图象与直线有3个交点
11.
我们学过用角度制与弧度制度量角,最近,有学者提出用“面度制”度量角,因为在半径不同的同心圆中,同样的圆心角所对扇形的面积与半径平方之比是常数,从而称这个常数为该角的面度数,这种用面度作为单位来度量角的单位制,叫做面度制在面度制下,角面度数为,则(
)
A.
B.
C.
D.
12.
在古希腊数学家海伦的著作《测地术》中记载了著名的海伦公式,利用三角形的三边长求三角形的面积,若三角形的三边长分别为,,,则其面积,其中,现有一个三角形边长,,满足,,则此三角形面积最大值为(
)
A.
B.
C.
D.
第Ⅱ卷(非选择题)
二、填空题(共20分)
13.
已知函数在区间上有最大值6,最小值5,则实数的取值范围是__________.
14.
函数是幂函数且为偶函数,则的值为___________.
15.
已知函数,若,则__________.
16.
下列说法正确的序号是:__________.
①偶函数的定义域为,则;
②一次函数满足,则函数的解析式为;
③奇函数在上单调递增,且最大值为8,最小值为-1,则;
④若集合中至多有一个元素,则.
三、解答题(共70分)
17.
已知全集,集合,集合.
(1)若,求,;
(2)若,求实数的取值范围.
18.
已知函数,并且的解集也是不等式解集.
(1)求的解析式;
(2)若在区间上不单调,求实数的取值范围.
19.
已知,,,.
(1)求的值;
(2)求的值.
20.
已知函数,在一周期内,当时,取得最大值3,当时,取得最小值-3,求:
(1)函数的解析式;
(2)求出函数的单调递增区间、对称轴方程、对称中心坐标;
(3)当时,求函数的值域.
21.
已知锐角内角,,及对边,,,满足.
(1)求的大小;
(2)若,求的取值范围.
22.
已知函数为,其中为常数.
(1)当时,求的最大值;
(2)若在区间(为自然对数的底数)上的最大值为-3,求的值.
汉台高中2022届高三第一次月考文科数学参考答案
一、选择题:
1-5:ADDCB
6-10:DBAAC
11-12:BD
二、填空题:
13.
14.
-1
15.
-3
16.
①③
三、解答题:
17.【详解】(1)由题意,
当时,,则,
所以,;
(2)若,则,
∴,解得,∴实数的取值范围是.
18.【详解】(1)不等式的解集为,
依题意,方程的两个根为-3和2,则,
由根与系数关系可得:,解得,
所以的解析式为;
(2)由(1)可知函数的图象的对称轴为,
若在区间上不单调,则有,解得,
所以实数的取值范围是.
19.【详解】(1)∵,
;
(2)由,可得,,
则;
,
则
.
20.【详解】(1)由题设知,,周期,,由得.
所以.
又因为时,取得最大值3,
即,∴,解得,又,
所以,所以.
(2)由,得,
所以函数的单调递增区间为.
由,,得,.
对称轴方程为,.
由,得.
所以,该函数的对称中心为.
(3)因为,所以,则,
所以,所以值域为:.
所以函数的值域为.
21.【详解】(1)因为,
由正弦定理可得,
又因为,
所以,
可得,由,可得.
(2)因为,,
由正弦定理,可得,,
可得,
因为锐角三角形中,所以,解得,所以,
所以,可得.
22.【详解】(1)∵,∴.
当时,,.
当时,;当时,.
∴在上是增函数,在上是减函数,.
(2)∵,,∴.
①若,则,在上是增函数,
∴.不合题意.
②若,则由,即,
由,即.
从而在上为增函数,在上为减函数,
∴.
令,则,∴,即.
∵,∴为所求.
同课章节目录
