2020-2021学年华东师大版八年级数学上册12.1 幂的运算同步习题 (word解析版)
文档属性
| 名称 | 2020-2021学年华东师大版八年级数学上册12.1 幂的运算同步习题 (word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-04 17:59:59 | ||
图片预览




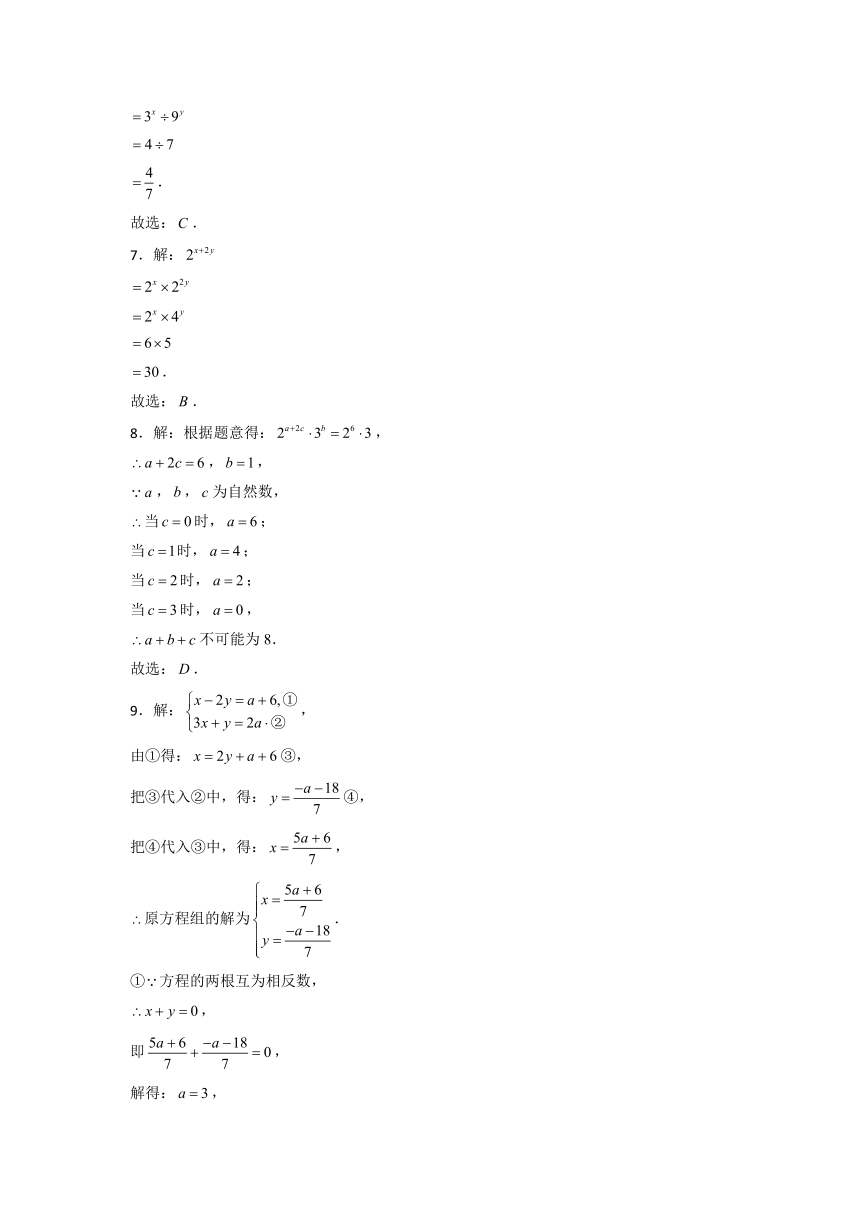
文档简介
《12.1
幂的运算》同步习题2020-2021年数学华东师大新版八(上)
一.选择题(共10小题)
1.下列计算正确的是
A.
B.
C.
D.
2.计算得
A.0.8
B.
C.
D.
3.若不为0,则
A.
B.
C.
D.
4.已知,,,则,,大小关系是
A.
B.
C.
D.
5.若,则下列正确的是
A.
B.
C.,
D.,
6.若,,则的值为
A.
B.
C.
D.
7.已知,,那么的值是
A.11
B.30
C.150
D.15
8.已知,,为自然数,且满足,则的取值不可能是
A.5
B.6
C.7
D.8
9.在关于,的二元一次方程组的下列说法中,正确的是
①当时,方程的两根互为相反数;②当且仅当时,解得与相等;③,满足关系式;④若,则.
A.①③
B.①②
C.①②③
D.①②③④
10.我们知道,同底数幂的乘法法则为(其中,、为正整数),类似地我们规定关于任意正整数、的一种新运算:;比如(2),则(4),若(2),那么的结果是
A.
B.
C.
D.
二.填空题(共8小题)
11.若,则 .
12.若,则的值为
.
13.已知,,则的值 .
14.若,,则 .
15.已知,,那么
.
16.若,则等于
.
17.若,则的值为
.
18.已知,,则
.
三.解答题(共8小题)
19.计算.
20.计算
(1)
(2)
(3);
(4).
21.已知常数、满足,且,求的值.
22.我们规定:,例如,请解决以下问题:
(1)试求的值.
(2)想一想与相等吗?请说明理由.
23.为了求的值,可令,则,因此,所以仿照以上推理,计算的值.
24.已知,求证:.
25.定义:如果,为正数),那么我们把叫做的数,记作.
(1)根据数的定义,填空:(2) , .
(2)数有如下运算性质:,,其中.
根据运算性质,计算:
①若(a),求;
②若已知(3),(5),试求,,,的值(用、、表示).
26.阅读下列材料:
一般地,个相同的因数相乘记为.如,此时,3叫做以2为底8的对数,记为(即.一般地,若且,,则叫做以为底的对数,记为(即.如,则4叫做以3为底81的对数,记为(即.
(1)计算以下各对数的值:
, , .
(2)观察(1)中三数4、16、64之间满足怎样的关系式,、、之间又满足怎样的关系式;
(3)由(2)的结果,你能归纳出一个一般性的结论吗?
;且,,
(4)根据幂的运算法则:以及对数的含义证明上述结论.
参考答案
一.选择题(共10小题)
1.解:、,故错误,不符合题意;
、,故错误,不符合题意;
、,故正确,符合题意;
、,故错误,不符合题意.
故选:.
2.解:原式
.
即为0.8.
故选:.
3.解:若不为0,则.
故选:.
4.解:,
,
,
,
,
故选:.
5.解:,
,
,
,
故选:.
6.解:原式
.
故选:.
7.解:
.
故选:.
8.解:根据题意得:,
,,
,,为自然数,
当时,;
当时,;
当时,;
当时,,
不可能为8.
故选:.
9.解:,
由①得:③,
把③代入②中,得:④,
把④代入③中,得:,
原方程组的解为.
①方程的两根互为相反数,
,
即,
解得:,
①正确;
②当与相等时,,
即,
解得:,
②正确;
③在原方程中,我们消去,得到,的关系,
②①得:,
③正确;
④,
,
,
,
,
将方程组的解代入得:,
解得:,
④正确.
综上所述,①②③④都正确.
故选:.
10.解:(2),,
,
故选:.
二.填空题(共8小题)
11.解:,
,
.
故答案为:2.
12.解:,,
.
.
故答案为:.
13.解:,,
,
.
故答案为:256.
14.解:,,
.
故答案为.
15.解:,
,
.
故答案为:1.
16.解:,
,
.
故答案为:8.
17.解:,
,
,
,
,
.
故答案为:.
18.解:,,
,,
,,
,
,
三.解答题(共8小题)
19.解:
.
20.解:(1)
,
;
(2)
;
(3)
;
(4)
21.解:,
,
,
,
,
,
,
.
22.解:(1);
(2),
,
与相等.
23.解:令,
则,
,
,
则.
24.证明:,
,
①
同理可证:②
由①②两式得,
即,
.
25.解:(1),
(2),
,
,
故答案为:1;4.
(2)①,
.
.
.
②,
(3)(5)
,
.
,
(3)(3)(3)(2)(2)
(3)(2)
.
,
(3)(3)(3)(5)(2)(2)
(3)(5)(2)
,
26.解:(1),,;
(2),;
(3);
(4)证明:设,,
则,,
,
即.
幂的运算》同步习题2020-2021年数学华东师大新版八(上)
一.选择题(共10小题)
1.下列计算正确的是
A.
B.
C.
D.
2.计算得
A.0.8
B.
C.
D.
3.若不为0,则
A.
B.
C.
D.
4.已知,,,则,,大小关系是
A.
B.
C.
D.
5.若,则下列正确的是
A.
B.
C.,
D.,
6.若,,则的值为
A.
B.
C.
D.
7.已知,,那么的值是
A.11
B.30
C.150
D.15
8.已知,,为自然数,且满足,则的取值不可能是
A.5
B.6
C.7
D.8
9.在关于,的二元一次方程组的下列说法中,正确的是
①当时,方程的两根互为相反数;②当且仅当时,解得与相等;③,满足关系式;④若,则.
A.①③
B.①②
C.①②③
D.①②③④
10.我们知道,同底数幂的乘法法则为(其中,、为正整数),类似地我们规定关于任意正整数、的一种新运算:;比如(2),则(4),若(2),那么的结果是
A.
B.
C.
D.
二.填空题(共8小题)
11.若,则 .
12.若,则的值为
.
13.已知,,则的值 .
14.若,,则 .
15.已知,,那么
.
16.若,则等于
.
17.若,则的值为
.
18.已知,,则
.
三.解答题(共8小题)
19.计算.
20.计算
(1)
(2)
(3);
(4).
21.已知常数、满足,且,求的值.
22.我们规定:,例如,请解决以下问题:
(1)试求的值.
(2)想一想与相等吗?请说明理由.
23.为了求的值,可令,则,因此,所以仿照以上推理,计算的值.
24.已知,求证:.
25.定义:如果,为正数),那么我们把叫做的数,记作.
(1)根据数的定义,填空:(2) , .
(2)数有如下运算性质:,,其中.
根据运算性质,计算:
①若(a),求;
②若已知(3),(5),试求,,,的值(用、、表示).
26.阅读下列材料:
一般地,个相同的因数相乘记为.如,此时,3叫做以2为底8的对数,记为(即.一般地,若且,,则叫做以为底的对数,记为(即.如,则4叫做以3为底81的对数,记为(即.
(1)计算以下各对数的值:
, , .
(2)观察(1)中三数4、16、64之间满足怎样的关系式,、、之间又满足怎样的关系式;
(3)由(2)的结果,你能归纳出一个一般性的结论吗?
;且,,
(4)根据幂的运算法则:以及对数的含义证明上述结论.
参考答案
一.选择题(共10小题)
1.解:、,故错误,不符合题意;
、,故错误,不符合题意;
、,故正确,符合题意;
、,故错误,不符合题意.
故选:.
2.解:原式
.
即为0.8.
故选:.
3.解:若不为0,则.
故选:.
4.解:,
,
,
,
,
故选:.
5.解:,
,
,
,
故选:.
6.解:原式
.
故选:.
7.解:
.
故选:.
8.解:根据题意得:,
,,
,,为自然数,
当时,;
当时,;
当时,;
当时,,
不可能为8.
故选:.
9.解:,
由①得:③,
把③代入②中,得:④,
把④代入③中,得:,
原方程组的解为.
①方程的两根互为相反数,
,
即,
解得:,
①正确;
②当与相等时,,
即,
解得:,
②正确;
③在原方程中,我们消去,得到,的关系,
②①得:,
③正确;
④,
,
,
,
,
将方程组的解代入得:,
解得:,
④正确.
综上所述,①②③④都正确.
故选:.
10.解:(2),,
,
故选:.
二.填空题(共8小题)
11.解:,
,
.
故答案为:2.
12.解:,,
.
.
故答案为:.
13.解:,,
,
.
故答案为:256.
14.解:,,
.
故答案为.
15.解:,
,
.
故答案为:1.
16.解:,
,
.
故答案为:8.
17.解:,
,
,
,
,
.
故答案为:.
18.解:,,
,,
,,
,
,
三.解答题(共8小题)
19.解:
.
20.解:(1)
,
;
(2)
;
(3)
;
(4)
21.解:,
,
,
,
,
,
,
.
22.解:(1);
(2),
,
与相等.
23.解:令,
则,
,
,
则.
24.证明:,
,
①
同理可证:②
由①②两式得,
即,
.
25.解:(1),
(2),
,
,
故答案为:1;4.
(2)①,
.
.
.
②,
(3)(5)
,
.
,
(3)(3)(3)(2)(2)
(3)(2)
.
,
(3)(3)(3)(5)(2)(2)
(3)(5)(2)
,
26.解:(1),,;
(2),;
(3);
(4)证明:设,,
则,,
,
即.
