1.8三角函数的简单应用 同步练习2020-2021学年高一下学期数学北师大版(2019)必修第二册(Word含答案解析)
文档属性
| 名称 | 1.8三角函数的简单应用 同步练习2020-2021学年高一下学期数学北师大版(2019)必修第二册(Word含答案解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 418.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-05 00:00:00 | ||
图片预览




文档简介
三角函数的简单应用
1.如图,是一向右传播的绳波在某一时刻绳子各点的位置图,经过周期后,乙的位置将移至( )
A.甲
B.乙
C.丙
D.丁
2.电流强度I(安)随时间t(秒)变化的函数I=Asin(ωt+φ)(A>0,ω>0,0<φ<)的图象如图所示,则当t=秒时,电流强度是( )
A.-5安
B.5安
C.5
安
D.10安
3.若近似认为月球绕地球公转与地球绕太阳公转的轨道在同一平面内,且均为正圆,又知这两种转动同向,如图所示,月相变化的周期为29.5天(如图是相继两次满月时,月、地、日相对位置的示意图).则月球绕地球一周所用的时间T为( )
A.24.5天
B.29.5天
C.28.5天
D.24天
4.为了研究钟表与三角函数的关系,建立如图所示的坐标系,设秒针位置为P(x,y).若初始位置为P0,当秒针从P0(注:此时t=0)开始走时,点P的纵坐标y与时间t的函数解析式可以是( )
A.y=sin
B.y=sin
C.y=sin
D.y=sin
5.如图,某港口一天6时到18时的水深变化曲线近似满足函数y=3sin+k.据此函数可知,这段时间水深(单位:m)的最大值为( )
A.5
B.6
C.8
D.10
6.某人的血压满足函数关系式f(t)=24sin
160πt+110,其中f(t)为血压,t为时间,则此人每分钟心跳的次数为________.
7.弹簧振子以O点为平衡位置,在B、C间做简谐振动,B、C相距20
cm,某时刻振子处在B点,经0.5
s振子首次达到C点,则振子在5秒内通过的路程及5
s末相对平衡位置的位移大小分别为________cm,________cm.
8.某时钟的秒针端点A到中心点O的距离为5
cm,秒针均匀地绕点O旋转,当时间t=0时,点A与钟面上标有12的点B重合,将A、B两点的距离d(cm)表示成t(s)的函数,则d=________,其中t∈[0,60].
9.如图所示,某地夏天8~14时用电量变化曲线近似满足函数y=Asin(ωx+φ)+bA>0,ω>0,|φ|<.
(1)求这一天的最大用电量及最小用电量;
(2)写出这段曲线的函数解析式.
10.下表是某地某年月平均气温(华氏):
月份
1
2
3
4
5
6
平均气温
21.4
26.0
36.0
48.8
59.1
68.6
月份
7
8
9
10
11
12
平均气温
73.0
71.9
64.7
53.5
39.8
27.7
以月份为x轴(x=月份-1),以平均气温为y轴.
(1)用正弦曲线去拟合这些数据;
(2)估计这个正弦曲线的周期T和振幅A;
(3)下面三个函数模型中,哪一个最适合这些数据?
①=cos;②=cos;③=cos.
11.如图所示,某风车的半径为2
m,每12
s旋转一周,它的最低点O距离地面0.5
m.风车圆周上一点A从最低点O开始,运动t(s)后与地面的距离为h(m).则h与t满足的函数关系为( )
A.h=sin+2.5
B.h=2sin+1.5
C.h=-2cost+2.5
D.h=2cost+2.5
12.如图所示,有一广告气球,直径为6
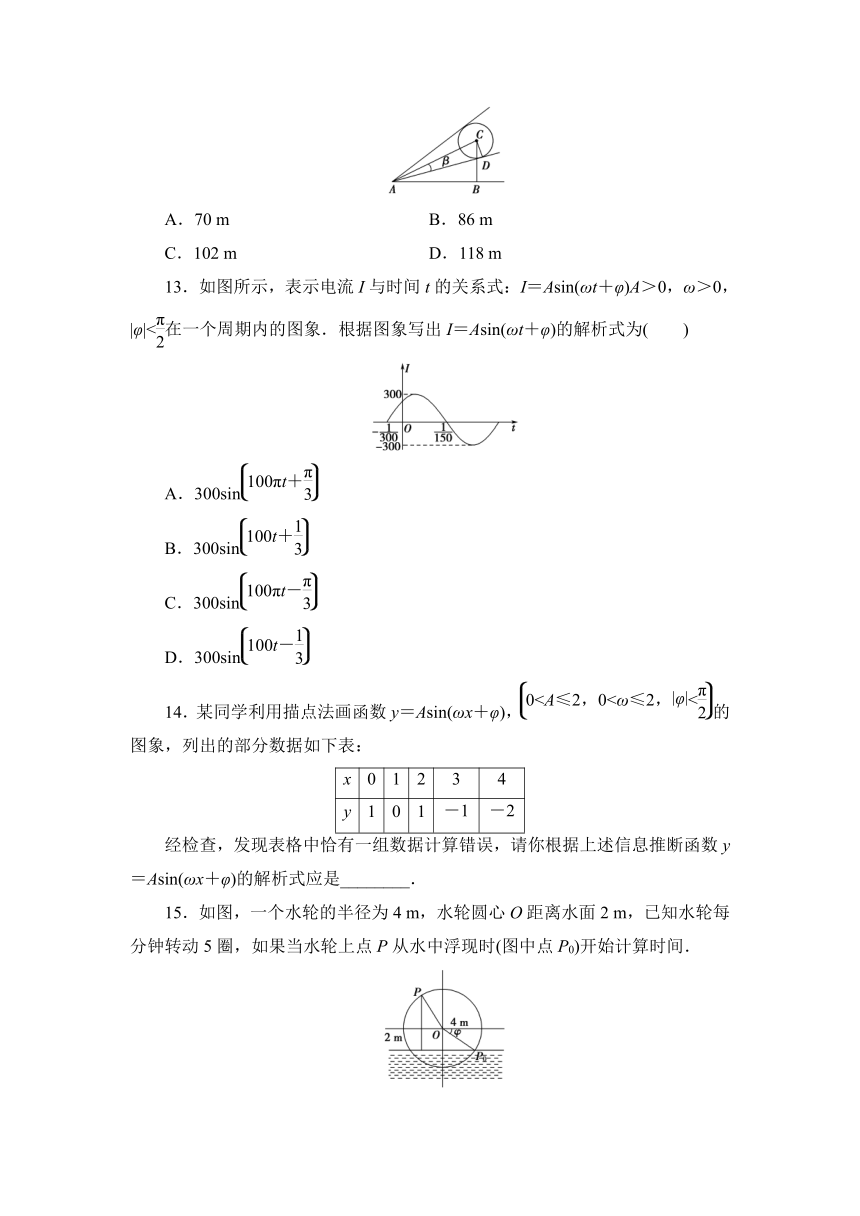
m,放在公司大楼上空,当行人仰望气球中心的仰角∠BAC=30°时,测得气球的视角为β=1°,当θ很小时,可取sin
θ≈θ,试估算气球的高BC的值约为( )
A.70
m
B.86
m
C.102
m
D.118
m
13.如图所示,表示电流I与时间t的关系式:I=Asin(ωt+φ)A>0,ω>0,|φ|<在一个周期内的图象.根据图象写出I=Asin(ωt+φ)的解析式为( )
A.300sin
B.300sin
C.300sin
D.300sin
14.某同学利用描点法画函数y=Asin(ωx+φ),的图象,列出的部分数据如下表:
x
0
1
2
3
4
y
1
0
1
-1
-2
经检查,发现表格中恰有一组数据计算错误,请你根据上述信息推断函数y=Asin(ωx+φ)的解析式应是________.
15.如图,一个水轮的半径为4
m,水轮圆心O距离水面2
m,已知水轮每分钟转动5圈,如果当水轮上点P从水中浮现时(图中点P0)开始计算时间.
(1)将点P距离水面的高度z(m)表示为时间t(s)的函数;
(2)点P第一次到达最高点大约需要多少时间?
答案
1.如图,是一向右传播的绳波在某一时刻绳子各点的位置图,经过周期后,乙的位置将移至( )
A.甲
B.乙
C.丙
D.丁
C [该题目考察了最值与周期间的关系;相邻的最大值与最小值之间间隔区间长度相差半个周期,选C.]
2.电流强度I(安)随时间t(秒)变化的函数I=Asin(ωt+φ)(A>0,ω>0,0<φ<)的图象如图所示,则当t=秒时,电流强度是( )
A.-5安
B.5安
C.5
安
D.10安
A [由图象知A=10,=-=,∴ω==100π,∴I=10sin(100πt+φ).
又(,10)为五点中的第二个点,
∴100π×
+φ=.
∴φ=,∴I=10sin,
当t=秒时,I=-5安.]
3.若近似认为月球绕地球公转与地球绕太阳公转的轨道在同一平面内,且均为正圆,又知这两种转动同向,如图所示,月相变化的周期为29.5天(如图是相继两次满月时,月、地、日相对位置的示意图).则月球绕地球一周所用的时间T为( )
A.24.5天
B.29.5天
C.28.5天
D.24天
B [由题图知,地球从E1到E2用时29.5天,月球从月、地、日一条线重新回到月、地、日一条线,完成一个周期.]
4.为了研究钟表与三角函数的关系,建立如图所示的坐标系,设秒针位置为P(x,y).若初始位置为P0,当秒针从P0(注:此时t=0)开始走时,点P的纵坐标y与时间t的函数解析式可以是( )
A.y=sin
B.y=sin
C.y=sin
D.y=sin
C [由题意知,函数的周期为T=60,∴|ω|==.
设函数解析式为y=sin.
∵初始位置为P0,
∴t=0时,y=,∴sin
φ=,∴φ可取,
∴函数解析式可以是y=sin.
又由秒针顺时针转动可知,y的值从t=0开始要先逐渐减小,
故y=sin.]
5.如图,某港口一天6时到18时的水深变化曲线近似满足函数y=3sin+k.据此函数可知,这段时间水深(单位:m)的最大值为( )
A.5
B.6
C.8
D.10
C [根据图象得函数的最小值为2,有-3+k=2,k=5,最大值为3+5=8.]
6.某人的血压满足函数关系式f(t)=24sin
160πt+110,其中f(t)为血压,t为时间,则此人每分钟心跳的次数为________.
80 [∵T==,∴f==80.]
7.弹簧振子以O点为平衡位置,在B、C间做简谐振动,B、C相距20
cm,某时刻振子处在B点,经0.5
s振子首次达到C点,则振子在5秒内通过的路程及5
s末相对平衡位置的位移大小分别为________cm,________cm.
200 10 [振幅A=10,T=0.5×2=1,每个周期通过的路程为40
cm,5秒内通过200
cm;经过5个周期仍回到初始位置B,位移为10
cm.]
8.某时钟的秒针端点A到中心点O的距离为5
cm,秒针均匀地绕点O旋转,当时间t=0时,点A与钟面上标有12的点B重合,将A、B两点的距离d(cm)表示成t(s)的函数,则d=________,其中t∈[0,60].
10sin [解析式可写为d=Asin(ωt+φ)的形式,由题意易知A=10,当t=0时,d=0,得φ=0;当t=30时,d=10,可得ω=,所以d=10sin.]
9.如图所示,某地夏天8~14时用电量变化曲线近似满足函数y=Asin(ωx+φ)+bA>0,ω>0,|φ|<.
(1)求这一天的最大用电量及最小用电量;
(2)写出这段曲线的函数解析式.
[解] (1)由题图可知,一天最大用电量为50万度,最小用电量为30万度.
(2)b==40,A×1+40=50A=10,
由图可知,=14-8=6,则T=12,ω==,
则y=10sin+40,代入(8,30)得φ=,
∴解析式为y=10sin+40,x∈[8,14].
10.下表是某地某年月平均气温(华氏):
月份
1
2
3
4
5
6
平均气温
21.4
26.0
36.0
48.8
59.1
68.6
月份
7
8
9
10
11
12
平均气温
73.0
71.9
64.7
53.5
39.8
27.7
以月份为x轴(x=月份-1),以平均气温为y轴.
(1)用正弦曲线去拟合这些数据;
(2)估计这个正弦曲线的周期T和振幅A;
(3)下面三个函数模型中,哪一个最适合这些数据?
①=cos;②=cos;③=cos.
[解] (1)如图.
(2)最低气温为1月份21.4,最高气温为7月份73.0,
故=7-1=6,所以T=12.
因为2A的值等于最高气温与最低气温的差,即2A=73.0-21.4=51.6,
所以A=25.8.
(3)因为x=月份-1,所以不妨取x=2-1=1,y=26.0.
代入①,得=>1≠cos,故①不适合;代入②,得=<0≠cos,故②不适合.所以应选③.
11.如图所示,某风车的半径为2
m,每12
s旋转一周,它的最低点O距离地面0.5
m.风车圆周上一点A从最低点O开始,运动t(s)后与地面的距离为h(m).则h与t满足的函数关系为( )
A.h=sin+2.5
B.h=2sin+1.5
C.h=-2cost+2.5
D.h=2cost+2.5
C [最大值M=4.5
m,最小值m=0.5
m,所以A==2,b==2.5,因为T=12,所以ω==,又风车从最低点开始运动,所以
×0+φ=2kπ+(k∈Z),不妨设φ=,所以h与t满足的函数关系为h=2sin+2.5=-2cost+2.5.]
12.如图所示,有一广告气球,直径为6
m,放在公司大楼上空,当行人仰望气球中心的仰角∠BAC=30°时,测得气球的视角为β=1°,当θ很小时,可取sin
θ≈θ,试估算气球的高BC的值约为( )
A.70
m
B.86
m
C.102
m
D.118
m
B [AC==≈×180≈172(m),又∠BAC=30°,∴BC=AC=86
m.]
13.如图所示,表示电流I与时间t的关系式:I=Asin(ωt+φ)A>0,ω>0,|φ|<在一个周期内的图象.根据图象写出I=Asin(ωt+φ)的解析式为( )
A.300sin
B.300sin
C.300sin
D.300sin
A [由图象可知A=300,又T=2=,∴ω==100π.
又∵t=-时,I=0,
∴100π(-)+φ=2kπ,k∈Z,即φ=,
∴I=300sin.]
14.某同学利用描点法画函数y=Asin(ωx+φ),的图象,列出的部分数据如下表:
x
0
1
2
3
4
y
1
0
1
-1
-2
经检查,发现表格中恰有一组数据计算错误,请你根据上述信息推断函数y=Asin(ωx+φ)的解析式应是________.
y=2sin [在平面直角坐标系中描出这五个点,如图所示.
根据函数图象的大致走势,
可知点(1,0)不符合题意;又∵0∴A=2,
∵函数图象过点(0,1),
∴2sin
φ=1.又∵-<φ<,∴φ=,
由(0,1),(2,1)关于直线x=1对称,知x=1时函数取得最大值2,
∴函数的最小正周期为6.
∴ω=,∴函数的解析式为y=2sinx+.]
15.如图,一个水轮的半径为4
m,水轮圆心O距离水面2
m,已知水轮每分钟转动5圈,如果当水轮上点P从水中浮现时(图中点P0)开始计算时间.
(1)将点P距离水面的高度z(m)表示为时间t(s)的函数;
(2)点P第一次到达最高点大约需要多少时间?
[解] (1)如图所示建立直角坐标系,设角φ是以Ox为始边,OP0为终边的角.
OP每秒钟内所转过的角为=.
则OP在时间t(s)内所转过的角为t.
由题意可知水轮逆时针转动,
得z=4sin+2.
当t=0时,z=0,得sin
φ=-,即φ=-.
故所求的函数关系式为z=4sin+2.
(2)令z=4sin+2=6,
得sin=1,令t-=,得t=4,
故点P第一次到达最高点大约需要4
s.
1.如图,是一向右传播的绳波在某一时刻绳子各点的位置图,经过周期后,乙的位置将移至( )
A.甲
B.乙
C.丙
D.丁
2.电流强度I(安)随时间t(秒)变化的函数I=Asin(ωt+φ)(A>0,ω>0,0<φ<)的图象如图所示,则当t=秒时,电流强度是( )
A.-5安
B.5安
C.5
安
D.10安
3.若近似认为月球绕地球公转与地球绕太阳公转的轨道在同一平面内,且均为正圆,又知这两种转动同向,如图所示,月相变化的周期为29.5天(如图是相继两次满月时,月、地、日相对位置的示意图).则月球绕地球一周所用的时间T为( )
A.24.5天
B.29.5天
C.28.5天
D.24天
4.为了研究钟表与三角函数的关系,建立如图所示的坐标系,设秒针位置为P(x,y).若初始位置为P0,当秒针从P0(注:此时t=0)开始走时,点P的纵坐标y与时间t的函数解析式可以是( )
A.y=sin
B.y=sin
C.y=sin
D.y=sin
5.如图,某港口一天6时到18时的水深变化曲线近似满足函数y=3sin+k.据此函数可知,这段时间水深(单位:m)的最大值为( )
A.5
B.6
C.8
D.10
6.某人的血压满足函数关系式f(t)=24sin
160πt+110,其中f(t)为血压,t为时间,则此人每分钟心跳的次数为________.
7.弹簧振子以O点为平衡位置,在B、C间做简谐振动,B、C相距20
cm,某时刻振子处在B点,经0.5
s振子首次达到C点,则振子在5秒内通过的路程及5
s末相对平衡位置的位移大小分别为________cm,________cm.
8.某时钟的秒针端点A到中心点O的距离为5
cm,秒针均匀地绕点O旋转,当时间t=0时,点A与钟面上标有12的点B重合,将A、B两点的距离d(cm)表示成t(s)的函数,则d=________,其中t∈[0,60].
9.如图所示,某地夏天8~14时用电量变化曲线近似满足函数y=Asin(ωx+φ)+bA>0,ω>0,|φ|<.
(1)求这一天的最大用电量及最小用电量;
(2)写出这段曲线的函数解析式.
10.下表是某地某年月平均气温(华氏):
月份
1
2
3
4
5
6
平均气温
21.4
26.0
36.0
48.8
59.1
68.6
月份
7
8
9
10
11
12
平均气温
73.0
71.9
64.7
53.5
39.8
27.7
以月份为x轴(x=月份-1),以平均气温为y轴.
(1)用正弦曲线去拟合这些数据;
(2)估计这个正弦曲线的周期T和振幅A;
(3)下面三个函数模型中,哪一个最适合这些数据?
①=cos;②=cos;③=cos.
11.如图所示,某风车的半径为2
m,每12
s旋转一周,它的最低点O距离地面0.5
m.风车圆周上一点A从最低点O开始,运动t(s)后与地面的距离为h(m).则h与t满足的函数关系为( )
A.h=sin+2.5
B.h=2sin+1.5
C.h=-2cost+2.5
D.h=2cost+2.5
12.如图所示,有一广告气球,直径为6
m,放在公司大楼上空,当行人仰望气球中心的仰角∠BAC=30°时,测得气球的视角为β=1°,当θ很小时,可取sin
θ≈θ,试估算气球的高BC的值约为( )
A.70
m
B.86
m
C.102
m
D.118
m
13.如图所示,表示电流I与时间t的关系式:I=Asin(ωt+φ)A>0,ω>0,|φ|<在一个周期内的图象.根据图象写出I=Asin(ωt+φ)的解析式为( )
A.300sin
B.300sin
C.300sin
D.300sin
14.某同学利用描点法画函数y=Asin(ωx+φ),的图象,列出的部分数据如下表:
x
0
1
2
3
4
y
1
0
1
-1
-2
经检查,发现表格中恰有一组数据计算错误,请你根据上述信息推断函数y=Asin(ωx+φ)的解析式应是________.
15.如图,一个水轮的半径为4
m,水轮圆心O距离水面2
m,已知水轮每分钟转动5圈,如果当水轮上点P从水中浮现时(图中点P0)开始计算时间.
(1)将点P距离水面的高度z(m)表示为时间t(s)的函数;
(2)点P第一次到达最高点大约需要多少时间?
答案
1.如图,是一向右传播的绳波在某一时刻绳子各点的位置图,经过周期后,乙的位置将移至( )
A.甲
B.乙
C.丙
D.丁
C [该题目考察了最值与周期间的关系;相邻的最大值与最小值之间间隔区间长度相差半个周期,选C.]
2.电流强度I(安)随时间t(秒)变化的函数I=Asin(ωt+φ)(A>0,ω>0,0<φ<)的图象如图所示,则当t=秒时,电流强度是( )
A.-5安
B.5安
C.5
安
D.10安
A [由图象知A=10,=-=,∴ω==100π,∴I=10sin(100πt+φ).
又(,10)为五点中的第二个点,
∴100π×
+φ=.
∴φ=,∴I=10sin,
当t=秒时,I=-5安.]
3.若近似认为月球绕地球公转与地球绕太阳公转的轨道在同一平面内,且均为正圆,又知这两种转动同向,如图所示,月相变化的周期为29.5天(如图是相继两次满月时,月、地、日相对位置的示意图).则月球绕地球一周所用的时间T为( )
A.24.5天
B.29.5天
C.28.5天
D.24天
B [由题图知,地球从E1到E2用时29.5天,月球从月、地、日一条线重新回到月、地、日一条线,完成一个周期.]
4.为了研究钟表与三角函数的关系,建立如图所示的坐标系,设秒针位置为P(x,y).若初始位置为P0,当秒针从P0(注:此时t=0)开始走时,点P的纵坐标y与时间t的函数解析式可以是( )
A.y=sin
B.y=sin
C.y=sin
D.y=sin
C [由题意知,函数的周期为T=60,∴|ω|==.
设函数解析式为y=sin.
∵初始位置为P0,
∴t=0时,y=,∴sin
φ=,∴φ可取,
∴函数解析式可以是y=sin.
又由秒针顺时针转动可知,y的值从t=0开始要先逐渐减小,
故y=sin.]
5.如图,某港口一天6时到18时的水深变化曲线近似满足函数y=3sin+k.据此函数可知,这段时间水深(单位:m)的最大值为( )
A.5
B.6
C.8
D.10
C [根据图象得函数的最小值为2,有-3+k=2,k=5,最大值为3+5=8.]
6.某人的血压满足函数关系式f(t)=24sin
160πt+110,其中f(t)为血压,t为时间,则此人每分钟心跳的次数为________.
80 [∵T==,∴f==80.]
7.弹簧振子以O点为平衡位置,在B、C间做简谐振动,B、C相距20
cm,某时刻振子处在B点,经0.5
s振子首次达到C点,则振子在5秒内通过的路程及5
s末相对平衡位置的位移大小分别为________cm,________cm.
200 10 [振幅A=10,T=0.5×2=1,每个周期通过的路程为40
cm,5秒内通过200
cm;经过5个周期仍回到初始位置B,位移为10
cm.]
8.某时钟的秒针端点A到中心点O的距离为5
cm,秒针均匀地绕点O旋转,当时间t=0时,点A与钟面上标有12的点B重合,将A、B两点的距离d(cm)表示成t(s)的函数,则d=________,其中t∈[0,60].
10sin [解析式可写为d=Asin(ωt+φ)的形式,由题意易知A=10,当t=0时,d=0,得φ=0;当t=30时,d=10,可得ω=,所以d=10sin.]
9.如图所示,某地夏天8~14时用电量变化曲线近似满足函数y=Asin(ωx+φ)+bA>0,ω>0,|φ|<.
(1)求这一天的最大用电量及最小用电量;
(2)写出这段曲线的函数解析式.
[解] (1)由题图可知,一天最大用电量为50万度,最小用电量为30万度.
(2)b==40,A×1+40=50A=10,
由图可知,=14-8=6,则T=12,ω==,
则y=10sin+40,代入(8,30)得φ=,
∴解析式为y=10sin+40,x∈[8,14].
10.下表是某地某年月平均气温(华氏):
月份
1
2
3
4
5
6
平均气温
21.4
26.0
36.0
48.8
59.1
68.6
月份
7
8
9
10
11
12
平均气温
73.0
71.9
64.7
53.5
39.8
27.7
以月份为x轴(x=月份-1),以平均气温为y轴.
(1)用正弦曲线去拟合这些数据;
(2)估计这个正弦曲线的周期T和振幅A;
(3)下面三个函数模型中,哪一个最适合这些数据?
①=cos;②=cos;③=cos.
[解] (1)如图.
(2)最低气温为1月份21.4,最高气温为7月份73.0,
故=7-1=6,所以T=12.
因为2A的值等于最高气温与最低气温的差,即2A=73.0-21.4=51.6,
所以A=25.8.
(3)因为x=月份-1,所以不妨取x=2-1=1,y=26.0.
代入①,得=>1≠cos,故①不适合;代入②,得=<0≠cos,故②不适合.所以应选③.
11.如图所示,某风车的半径为2
m,每12
s旋转一周,它的最低点O距离地面0.5
m.风车圆周上一点A从最低点O开始,运动t(s)后与地面的距离为h(m).则h与t满足的函数关系为( )
A.h=sin+2.5
B.h=2sin+1.5
C.h=-2cost+2.5
D.h=2cost+2.5
C [最大值M=4.5
m,最小值m=0.5
m,所以A==2,b==2.5,因为T=12,所以ω==,又风车从最低点开始运动,所以
×0+φ=2kπ+(k∈Z),不妨设φ=,所以h与t满足的函数关系为h=2sin+2.5=-2cost+2.5.]
12.如图所示,有一广告气球,直径为6
m,放在公司大楼上空,当行人仰望气球中心的仰角∠BAC=30°时,测得气球的视角为β=1°,当θ很小时,可取sin
θ≈θ,试估算气球的高BC的值约为( )
A.70
m
B.86
m
C.102
m
D.118
m
B [AC==≈×180≈172(m),又∠BAC=30°,∴BC=AC=86
m.]
13.如图所示,表示电流I与时间t的关系式:I=Asin(ωt+φ)A>0,ω>0,|φ|<在一个周期内的图象.根据图象写出I=Asin(ωt+φ)的解析式为( )
A.300sin
B.300sin
C.300sin
D.300sin
A [由图象可知A=300,又T=2=,∴ω==100π.
又∵t=-时,I=0,
∴100π(-)+φ=2kπ,k∈Z,即φ=,
∴I=300sin.]
14.某同学利用描点法画函数y=Asin(ωx+φ),的图象,列出的部分数据如下表:
x
0
1
2
3
4
y
1
0
1
-1
-2
经检查,发现表格中恰有一组数据计算错误,请你根据上述信息推断函数y=Asin(ωx+φ)的解析式应是________.
y=2sin [在平面直角坐标系中描出这五个点,如图所示.
根据函数图象的大致走势,
可知点(1,0)不符合题意;又∵0
∵函数图象过点(0,1),
∴2sin
φ=1.又∵-<φ<,∴φ=,
由(0,1),(2,1)关于直线x=1对称,知x=1时函数取得最大值2,
∴函数的最小正周期为6.
∴ω=,∴函数的解析式为y=2sinx+.]
15.如图,一个水轮的半径为4
m,水轮圆心O距离水面2
m,已知水轮每分钟转动5圈,如果当水轮上点P从水中浮现时(图中点P0)开始计算时间.
(1)将点P距离水面的高度z(m)表示为时间t(s)的函数;
(2)点P第一次到达最高点大约需要多少时间?
[解] (1)如图所示建立直角坐标系,设角φ是以Ox为始边,OP0为终边的角.
OP每秒钟内所转过的角为=.
则OP在时间t(s)内所转过的角为t.
由题意可知水轮逆时针转动,
得z=4sin+2.
当t=0时,z=0,得sin
φ=-,即φ=-.
故所求的函数关系式为z=4sin+2.
(2)令z=4sin+2=6,
得sin=1,令t-=,得t=4,
故点P第一次到达最高点大约需要4
s.
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
