6.3平面向量线性运算的应用练习题-2021-2022学年高中数学人教版B版(2019)必修第二册(Word含答案解析)
文档属性
| 名称 | 6.3平面向量线性运算的应用练习题-2021-2022学年高中数学人教版B版(2019)必修第二册(Word含答案解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 254.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-05 00:00:00 | ||
图片预览



文档简介
平面向量线性运算的应用
一、选择题
1.已知作用在点A的三个力F1=(3,4),F2=(2,-5),F3=(3,1)且A(1,1),则合力F=F1+F2+F3的终点坐标为( )
A.(9,1)
B.(1,9)
C.(9,0)
D.(0,9)
2.在△ABC中,若(++)=,则点G是△ABC的( )
A.内心
B.外心
C.垂心
D.重心
3.在五边形ABCDE中(如图),+-=( )
A.
B.
C.
D.
4.已知A(7,1),B(1,4),直线y=ax与线段AB交于点C,且=2,则a等于( )
A.2
B.1
C.
D.
5.炮弹的初速度为v0,发射角为θ,则炮弹上升的高度y与v0之间的关系式(t为飞行时间)为( )
A.y=|v0|t
B.y=|v0|sin
θ·t-|g|t2
C.y=|v0|sin
θ·t
D.y=|v0|cos
θ·t
二、填空题
6.一艘船从O点出发以2
km/h的速度向垂直于对岸的方向行驶,而船实际行驶速度的大小为4
km/h,则河水的流速大小为________km/h.
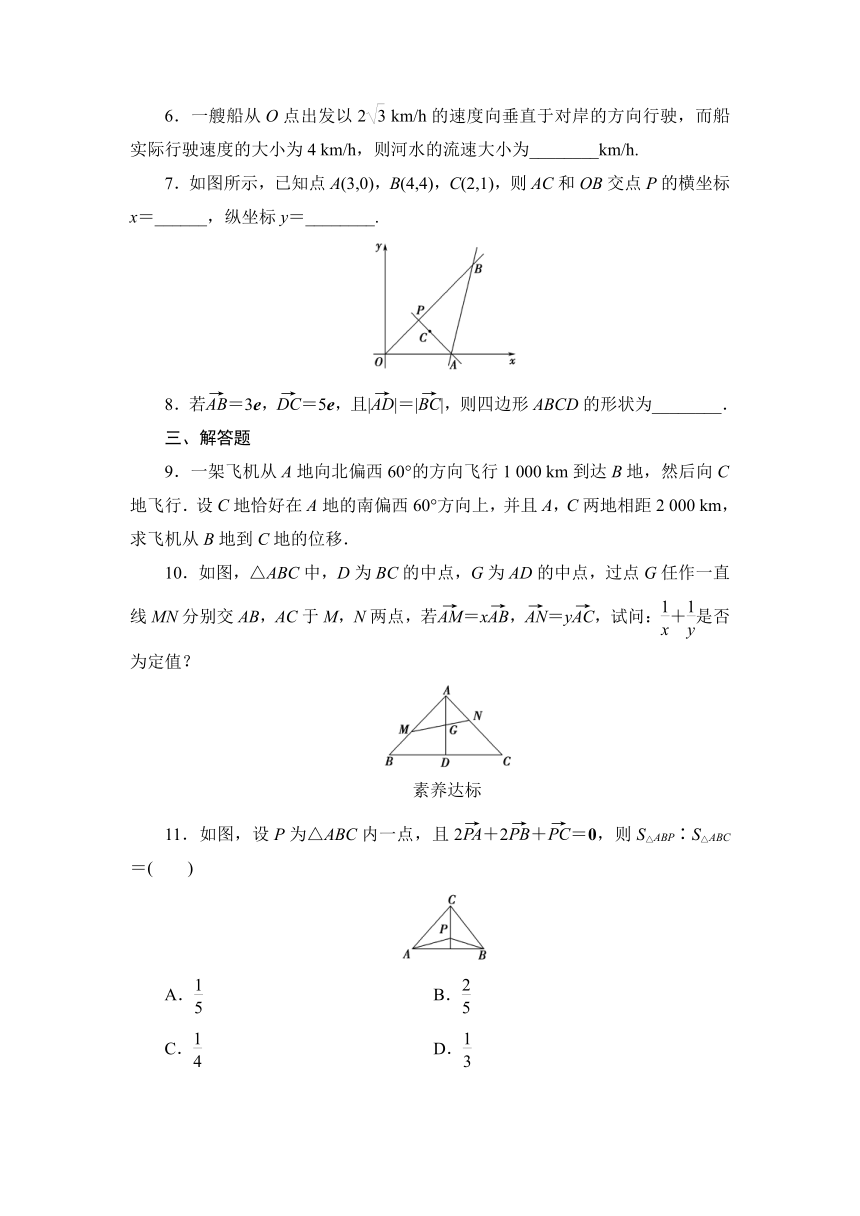
7.如图所示,已知点A(3,0),B(4,4),C(2,1),则AC和OB交点P的横坐标x=______,纵坐标y=________.
8.若=3e,=5e,且||=||,则四边形ABCD的形状为________.
三、解答题
9.一架飞机从A地向北偏西60°的方向飞行1
000
km到达B地,然后向C地飞行.设C地恰好在A地的南偏西60°方向上,并且A,C两地相距2
000
km,求飞机从B地到C地的位移.
10.如图,△ABC中,D为BC的中点,G为AD的中点,过点G任作一直线MN分别交AB,AC于M,N两点,若=x,=y,试问:+是否为定值?
素养达标
11.如图,设P为△ABC内一点,且2+2+=0,则S△ABP∶S△ABC=( )
A.
B.
C.
D.
12.点P是△ABC所在平面内一点,满足|-|-|+-2|=0,则△ABC的形状不可能是( )
A.钝角三角形
B.直角三角形
C.等腰三角形
D.等边三角形
13.某人骑车以每小时a千米的速度向东行驶,感到风从正北方向吹来,而当速度为2a时,感到风从东北方向吹来,则实际风速的大小为________,方向是________风.
14.已知△AOB,点P在直线AB上,且满足=2t+t(t∈R),则t=________.
15.如图所示,四边形ABCD是正方形,BE∥AC,AC=CE,EC的延长线交BA的延长线于F.求证:AF=AE.
一、选择题
1.已知作用在点A的三个力F1=(3,4),F2=(2,-5),F3=(3,1)且A(1,1),则合力F=F1+F2+F3的终点坐标为( )
A.(9,1)
B.(1,9)
C.(9,0)
D.(0,9)
A [F=F1+F2+F3=(8,0),又∵起点坐标为A(1,1),∴终点坐标为(9,1).]
2.在△ABC中,若(++)=,则点G是△ABC的( )
A.内心
B.外心
C.垂心
D.重心
D [因为(++)=,所以-+-+-=3,化简得++=0,故点G为△ABC的重心.]
3.在五边形ABCDE中(如图),+-=( )
A.
B.
C.
D.
B [+-=+=.]
4.已知A(7,1),B(1,4),直线y=ax与线段AB交于点C,且=2,则a等于( )
A.2
B.1
C.
D.
A [设C(x,y),则(x-7,y-1)=2(1-x,4-y)???
∴3=a×3?a=2.故选A.]
5.炮弹的初速度为v0,发射角为θ,则炮弹上升的高度y与v0之间的关系式(t为飞行时间)为( )
A.y=|v0|t
B.y=|v0|sin
θ·t-|g|t2
C.y=|v0|sin
θ·t
D.y=|v0|cos
θ·t
B [炮弹上升的速度的大小为|v0|sin
θ,所以上升的高度与时间t的关系是:y=|v0|sin
θ·t-|g|t2.]
二、填空题
6.一艘船从O点出发以2
km/h的速度向垂直于对岸的方向行驶,而船实际行驶速度的大小为4
km/h,则河水的流速大小为________km/h.
2 [如图,||=4,||=2,
则||==2.]
7.如图所示,已知点A(3,0),B(4,4),C(2,1),则AC和OB交点P的横坐标x=______,纵坐标y=________.
[设=t=t(4,4)=(4t,4t),
则=-=(4t-3,4t),
=(2,1)-(3,0)=(-1,1).
由,共线得(4t-3)×1-4t×(-1)=0,
解得t=.∴=(4t,4t)=.
∴P点坐标为.]
8.若=3e,=5e,且||=||,则四边形ABCD的形状为________.
等腰梯形 [由=3e,=5e,得∥,
又因为ABCD为四边形,≠,
所以AB∥DC,AB≠DC.
又||=||,得AD=BC,
所以四边形ABCD为等腰梯形.]
三、解答题
9.一架飞机从A地向北偏西60°的方向飞行1
000
km到达B地,然后向C地飞行.设C地恰好在A地的南偏西60°方向上,并且A,C两地相距2
000
km,求飞机从B地到C地的位移.
[解] 如图所示,设A地在东西基线和南北基线的交点处,
则A(0,0),B(-1
000cos
30°,1
000sin
30°)=(-500,500),
C(-2
000cos
30°,-2
000sin
30°)=(-1
000,-1
000),
∴=(-500,-1
500),
∴||==1
000(km).
∴飞机从B地到C地的位移大小是1
000
km,方向是南偏西30°.
10.如图,△ABC中,D为BC的中点,G为AD的中点,过点G任作一直线MN分别交AB,AC于M,N两点,若=x,=y,试问:+是否为定值?
[解] 设=a,=b,则=xa,=yb,
==(+)=(a+b),
所以=-=(a+b)-xa=a+b,=-=yb-xa=-xa+yb,
因为与共线,所以存在实数λ,使=λ,所以a+b=λ(-xa+yb)=-λxa+λyb.因为a与b不共线,
所以消去λ,得+=4,
所以+为定值.
素养达标
11.如图,设P为△ABC内一点,且2+2+=0,则S△ABP∶S△ABC=( )
A.
B.
C.
D.
A [设AB的中点是D(图略),
∵+=2=-,∴=-,
∴P为CD的五等分点,∴△ABP的面积为△ABC的面积的.]
12.点P是△ABC所在平面内一点,满足|-|-|+-2|=0,则△ABC的形状不可能是( )
A.钝角三角形
B.直角三角形
C.等腰三角形
D.等边三角形
AD [∵P是△ABC所在平面内一点,且|-|-|+-2|=0,
∴||-|(-)+(-)|=0,
即||=|+|,
∴|-|=|+|,
由向量加法减法的几何意义知ABDC(+=)为矩形,∴⊥,
∴∠A=90°,则△ABC一定是直角三角形.故选AD.]
13.某人骑车以每小时a千米的速度向东行驶,感到风从正北方向吹来,而当速度为2a时,感到风从东北方向吹来,则实际风速的大小为________,方向是________风.
a 西北 [如图,设=-a,
=-2a,
∵+=,∴=v-a,这就是感到由正北方向吹来的风速.
∵+=,∴=v-2a,
于是当此人的速度是原来的2倍时所感受到由东北方向吹来的风速就是,
由题意知∠PBO=45°,PA⊥BO,BA=AO,从而△POB为等腰直角三角形.
∴PO=PB=a,即|v|=a,所以实际风速是大小为a的西北风.]
14.已知△AOB,点P在直线AB上,且满足=2t+t(t∈R),则t=________.
1 [=2t(-)+t,
(2t+1)=2t+t,
∴=+.
∵A,B,P三点共线,∴+=1,∴t=1.]
15.如图所示,四边形ABCD是正方形,BE∥AC,AC=CE,EC的延长线交BA的延长线于F.求证:AF=AE.
[证明] 如图,建立直角坐标系,设正方形的边长为1,则A(-1,1),B(0,1).
若设E(x,y),则=(x,y-1),=(1,-1).
又∵∥,∴x·(-1)-1×(y-1)=0,
∴x+y-1=0.又∵||=||,
∴x2+y2-2=0.
由得或(舍).
即E.
又设F(x′,1),由=(x′,1)和=共线得:x′-=0,得x′=-2-,∴F(-2-,1),
∴=(-1-,0),=,
∴||=eq
\r(\b\lc\(\rc\)(\a\vs4\al\co1(\f(3+\r(3),2)))+\b\lc\(\rc\)(\a\vs4\al\co1(\f(-1-\r(3),2))))=1+=||,∴AF=AE.
一、选择题
1.已知作用在点A的三个力F1=(3,4),F2=(2,-5),F3=(3,1)且A(1,1),则合力F=F1+F2+F3的终点坐标为( )
A.(9,1)
B.(1,9)
C.(9,0)
D.(0,9)
2.在△ABC中,若(++)=,则点G是△ABC的( )
A.内心
B.外心
C.垂心
D.重心
3.在五边形ABCDE中(如图),+-=( )
A.
B.
C.
D.
4.已知A(7,1),B(1,4),直线y=ax与线段AB交于点C,且=2,则a等于( )
A.2
B.1
C.
D.
5.炮弹的初速度为v0,发射角为θ,则炮弹上升的高度y与v0之间的关系式(t为飞行时间)为( )
A.y=|v0|t
B.y=|v0|sin
θ·t-|g|t2
C.y=|v0|sin
θ·t
D.y=|v0|cos
θ·t
二、填空题
6.一艘船从O点出发以2
km/h的速度向垂直于对岸的方向行驶,而船实际行驶速度的大小为4
km/h,则河水的流速大小为________km/h.
7.如图所示,已知点A(3,0),B(4,4),C(2,1),则AC和OB交点P的横坐标x=______,纵坐标y=________.
8.若=3e,=5e,且||=||,则四边形ABCD的形状为________.
三、解答题
9.一架飞机从A地向北偏西60°的方向飞行1
000
km到达B地,然后向C地飞行.设C地恰好在A地的南偏西60°方向上,并且A,C两地相距2
000
km,求飞机从B地到C地的位移.
10.如图,△ABC中,D为BC的中点,G为AD的中点,过点G任作一直线MN分别交AB,AC于M,N两点,若=x,=y,试问:+是否为定值?
素养达标
11.如图,设P为△ABC内一点,且2+2+=0,则S△ABP∶S△ABC=( )
A.
B.
C.
D.
12.点P是△ABC所在平面内一点,满足|-|-|+-2|=0,则△ABC的形状不可能是( )
A.钝角三角形
B.直角三角形
C.等腰三角形
D.等边三角形
13.某人骑车以每小时a千米的速度向东行驶,感到风从正北方向吹来,而当速度为2a时,感到风从东北方向吹来,则实际风速的大小为________,方向是________风.
14.已知△AOB,点P在直线AB上,且满足=2t+t(t∈R),则t=________.
15.如图所示,四边形ABCD是正方形,BE∥AC,AC=CE,EC的延长线交BA的延长线于F.求证:AF=AE.
一、选择题
1.已知作用在点A的三个力F1=(3,4),F2=(2,-5),F3=(3,1)且A(1,1),则合力F=F1+F2+F3的终点坐标为( )
A.(9,1)
B.(1,9)
C.(9,0)
D.(0,9)
A [F=F1+F2+F3=(8,0),又∵起点坐标为A(1,1),∴终点坐标为(9,1).]
2.在△ABC中,若(++)=,则点G是△ABC的( )
A.内心
B.外心
C.垂心
D.重心
D [因为(++)=,所以-+-+-=3,化简得++=0,故点G为△ABC的重心.]
3.在五边形ABCDE中(如图),+-=( )
A.
B.
C.
D.
B [+-=+=.]
4.已知A(7,1),B(1,4),直线y=ax与线段AB交于点C,且=2,则a等于( )
A.2
B.1
C.
D.
A [设C(x,y),则(x-7,y-1)=2(1-x,4-y)???
∴3=a×3?a=2.故选A.]
5.炮弹的初速度为v0,发射角为θ,则炮弹上升的高度y与v0之间的关系式(t为飞行时间)为( )
A.y=|v0|t
B.y=|v0|sin
θ·t-|g|t2
C.y=|v0|sin
θ·t
D.y=|v0|cos
θ·t
B [炮弹上升的速度的大小为|v0|sin
θ,所以上升的高度与时间t的关系是:y=|v0|sin
θ·t-|g|t2.]
二、填空题
6.一艘船从O点出发以2
km/h的速度向垂直于对岸的方向行驶,而船实际行驶速度的大小为4
km/h,则河水的流速大小为________km/h.
2 [如图,||=4,||=2,
则||==2.]
7.如图所示,已知点A(3,0),B(4,4),C(2,1),则AC和OB交点P的横坐标x=______,纵坐标y=________.
[设=t=t(4,4)=(4t,4t),
则=-=(4t-3,4t),
=(2,1)-(3,0)=(-1,1).
由,共线得(4t-3)×1-4t×(-1)=0,
解得t=.∴=(4t,4t)=.
∴P点坐标为.]
8.若=3e,=5e,且||=||,则四边形ABCD的形状为________.
等腰梯形 [由=3e,=5e,得∥,
又因为ABCD为四边形,≠,
所以AB∥DC,AB≠DC.
又||=||,得AD=BC,
所以四边形ABCD为等腰梯形.]
三、解答题
9.一架飞机从A地向北偏西60°的方向飞行1
000
km到达B地,然后向C地飞行.设C地恰好在A地的南偏西60°方向上,并且A,C两地相距2
000
km,求飞机从B地到C地的位移.
[解] 如图所示,设A地在东西基线和南北基线的交点处,
则A(0,0),B(-1
000cos
30°,1
000sin
30°)=(-500,500),
C(-2
000cos
30°,-2
000sin
30°)=(-1
000,-1
000),
∴=(-500,-1
500),
∴||==1
000(km).
∴飞机从B地到C地的位移大小是1
000
km,方向是南偏西30°.
10.如图,△ABC中,D为BC的中点,G为AD的中点,过点G任作一直线MN分别交AB,AC于M,N两点,若=x,=y,试问:+是否为定值?
[解] 设=a,=b,则=xa,=yb,
==(+)=(a+b),
所以=-=(a+b)-xa=a+b,=-=yb-xa=-xa+yb,
因为与共线,所以存在实数λ,使=λ,所以a+b=λ(-xa+yb)=-λxa+λyb.因为a与b不共线,
所以消去λ,得+=4,
所以+为定值.
素养达标
11.如图,设P为△ABC内一点,且2+2+=0,则S△ABP∶S△ABC=( )
A.
B.
C.
D.
A [设AB的中点是D(图略),
∵+=2=-,∴=-,
∴P为CD的五等分点,∴△ABP的面积为△ABC的面积的.]
12.点P是△ABC所在平面内一点,满足|-|-|+-2|=0,则△ABC的形状不可能是( )
A.钝角三角形
B.直角三角形
C.等腰三角形
D.等边三角形
AD [∵P是△ABC所在平面内一点,且|-|-|+-2|=0,
∴||-|(-)+(-)|=0,
即||=|+|,
∴|-|=|+|,
由向量加法减法的几何意义知ABDC(+=)为矩形,∴⊥,
∴∠A=90°,则△ABC一定是直角三角形.故选AD.]
13.某人骑车以每小时a千米的速度向东行驶,感到风从正北方向吹来,而当速度为2a时,感到风从东北方向吹来,则实际风速的大小为________,方向是________风.
a 西北 [如图,设=-a,
=-2a,
∵+=,∴=v-a,这就是感到由正北方向吹来的风速.
∵+=,∴=v-2a,
于是当此人的速度是原来的2倍时所感受到由东北方向吹来的风速就是,
由题意知∠PBO=45°,PA⊥BO,BA=AO,从而△POB为等腰直角三角形.
∴PO=PB=a,即|v|=a,所以实际风速是大小为a的西北风.]
14.已知△AOB,点P在直线AB上,且满足=2t+t(t∈R),则t=________.
1 [=2t(-)+t,
(2t+1)=2t+t,
∴=+.
∵A,B,P三点共线,∴+=1,∴t=1.]
15.如图所示,四边形ABCD是正方形,BE∥AC,AC=CE,EC的延长线交BA的延长线于F.求证:AF=AE.
[证明] 如图,建立直角坐标系,设正方形的边长为1,则A(-1,1),B(0,1).
若设E(x,y),则=(x,y-1),=(1,-1).
又∵∥,∴x·(-1)-1×(y-1)=0,
∴x+y-1=0.又∵||=||,
∴x2+y2-2=0.
由得或(舍).
即E.
又设F(x′,1),由=(x′,1)和=共线得:x′-=0,得x′=-2-,∴F(-2-,1),
∴=(-1-,0),=,
∴||=eq
\r(\b\lc\(\rc\)(\a\vs4\al\co1(\f(3+\r(3),2)))+\b\lc\(\rc\)(\a\vs4\al\co1(\f(-1-\r(3),2))))=1+=||,∴AF=AE.
