2020-2021学年河北省张家口市涿鹿县七年级(下)期末数学试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年河北省张家口市涿鹿县七年级(下)期末数学试卷(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 339.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-03 00:00:00 | ||
图片预览



文档简介
2020-2021学年河北省张家口市涿鹿县七年级(下)期末数学试卷
一、选择题(本大题共14个小题。每小题3分,共42分,在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.(3分)下面调查方式中,合适的是( )
A.调查你所在班级同学的身高,采用抽样调查方式
B.调查大汶河的水质情况,采用抽样调查的方式
C.调查CCTV﹣5《NBA
总决赛》栏目在我市的收视率,采用普查的方式
D.要了解全市初中学生的业余爱好,采用普查的方式
2.(3分)下列方程中是二元一次方程的是( )
A.x﹣5=3
B.x+=3
C.x+=1
D.xy=3
3.(3分)下列说法正确的是( )
A.a,b,c是直线,且a∥b,b∥c,则a∥c
B.a,b,c是直线,且a⊥b,b⊥c,则a⊥c
C.a,b,c是直线,且a∥b,b⊥c,则a∥c
D.a,b,c是直线,且a∥b,b∥c,则a⊥c
4.(3分)下列说法中,错误的是( )
A.4的算术平方根是2
B.的平方根是±9
C.8的平方根是
D.平方根等于1的实数是1
5.(3分)下列现象:①电梯的升降运动,②飞机在地面上沿直线滑行,③风车的转动,④冷水加热过程中气泡的上升.其中不属于平移的是( )
A.①②
B.①③
C.②③
D.③④
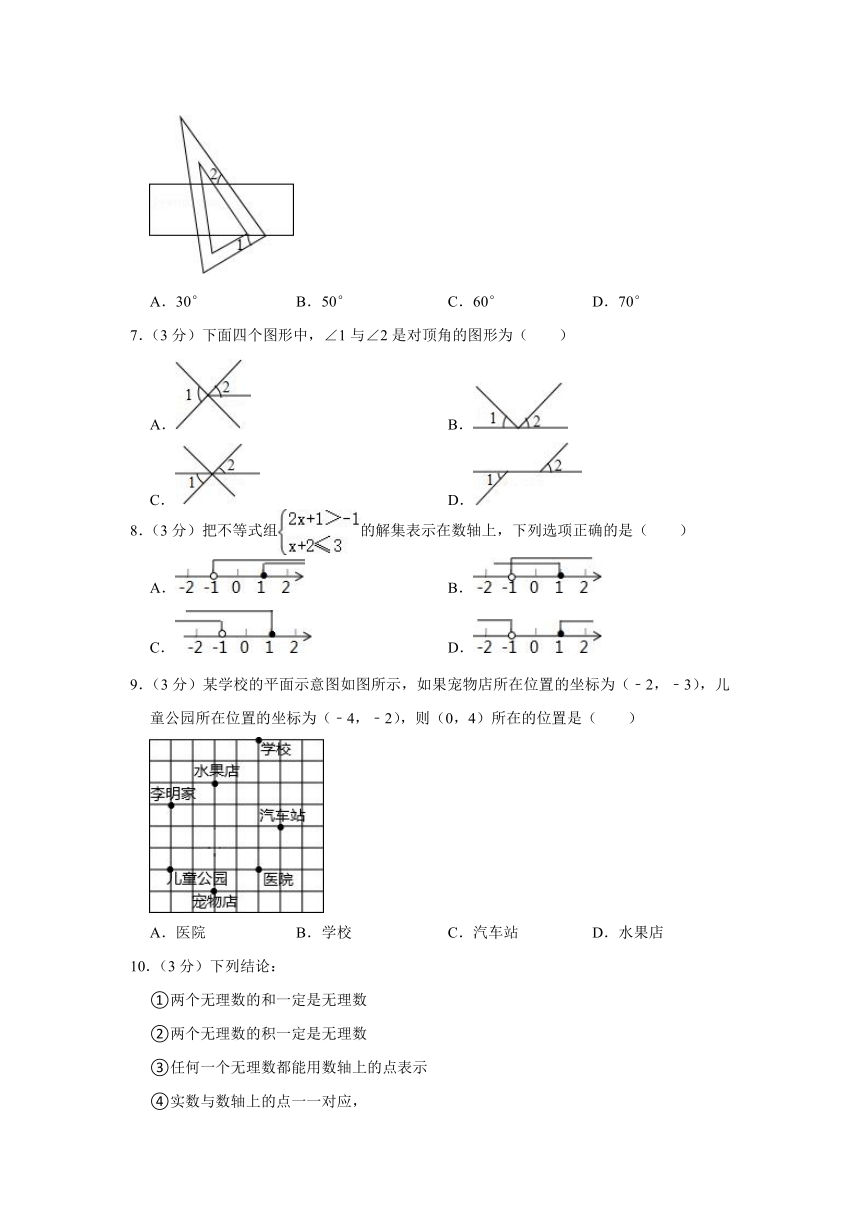
6.(3分)如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=30°,那么∠2的度数是( )
A.30°
B.50°
C.60°
D.70°
7.(3分)下面四个图形中,∠1与∠2是对顶角的图形为( )
A.
B.
C.
D.
8.(3分)把不等式组的解集表示在数轴上,下列选项正确的是( )
A.
B.
C.
D.
9.(3分)某学校的平面示意图如图所示,如果宠物店所在位置的坐标为(﹣2,﹣3),儿童公园所在位置的坐标为(﹣4,﹣2),则(0,4)所在的位置是( )
A.医院
B.学校
C.汽车站
D.水果店
10.(3分)下列结论:
①两个无理数的和一定是无理数
②两个无理数的积一定是无理数
③任何一个无理数都能用数轴上的点表示
④实数与数轴上的点一一对应,
其中正确的是( )
A.①②
B.②③
C.③④
D.②③④
11.(3分)甲,乙两人练习跑步,若乙先跑10米,则甲跑5秒就可以追上乙;如果乙先跑2秒,甲跑4秒就可以追上乙.设甲的速度为x米/秒,乙的速度为y米/秒,根据题意,下列选项中所列方程组正确的是( )
A.
B.
C.
D.
12.(3分)A、B、C是直线l上的三点,P是直线l外一点.若PA=5cm、PB=6cm、PC=8cm.由此可知,点P到直线l的距离是( )
A.5cm
B.不小于5cm
C.不大于5cm
D.在6cm与8cm之间
13.(3分)如图所示的运算程序中,如果开始输入的x值为﹣48,我们发现第1次输出的结果为﹣24,第2次输出的结果为﹣12,……,第2021次输出的结果为( )
A.﹣6
B.﹣3
C.﹣24
D.﹣12
14.(3分)利用两块长方体木块测量一张桌子的高度.首先按图1方式放置,再交换两木块的位置,按图2方式放置.测量的数据如图,则桌子的高度是( )
A.73cm
B.74cm
C.75cm
D.76cm
二、填空题(本大题共4个小题,每小题3分,共12分)
15.(3分)同一平面内的三条直线,其交点的个数可能为
.
16.(3分)把7的平方根和立方根按从小到大的顺序排列为
.
17.(3分)已知点A(4,y),B(x,﹣3),若AB∥x轴,且线段AB的长为5,x=
,y=
.
18.(3分)若关于x的不等式组的整数解共有3个,则a的取值范围为
.
三、解答题(本大题共6个小题,共66分,解答应写出必要的文字说明,证明过程及演算步骤)
19.(10分)解不等式组,并把它的解集在数轴上表示出来.
20.(10分)若方程组的解x与y是互为相反数,求k的值.
21.(12分)已知,如图,∠1=∠2,∠A=∠F.求证:∠C=∠D.
证明:∵∠1=∠2(已知)
∠1=∠3(
)
∴∠2=∠
(
)
∴BD∥
(
)
∴∠4=∠C
(
)
又∵∠A=
(已知)
∴AC∥
(
)
∴
=∠D(
)
∴∠C=∠D(
)
22.(10分)在“弘扬传统文化,打造书香校园”活动中,学校计划开展四项活动:“A﹣国学诵读”、“B﹣演讲”、“C﹣课本剧”、“D﹣书法”,要求每位同学必须且只能参加其中一项活动,学校为了了解学生的意愿,随机调查了部分学生,结果统计如下:
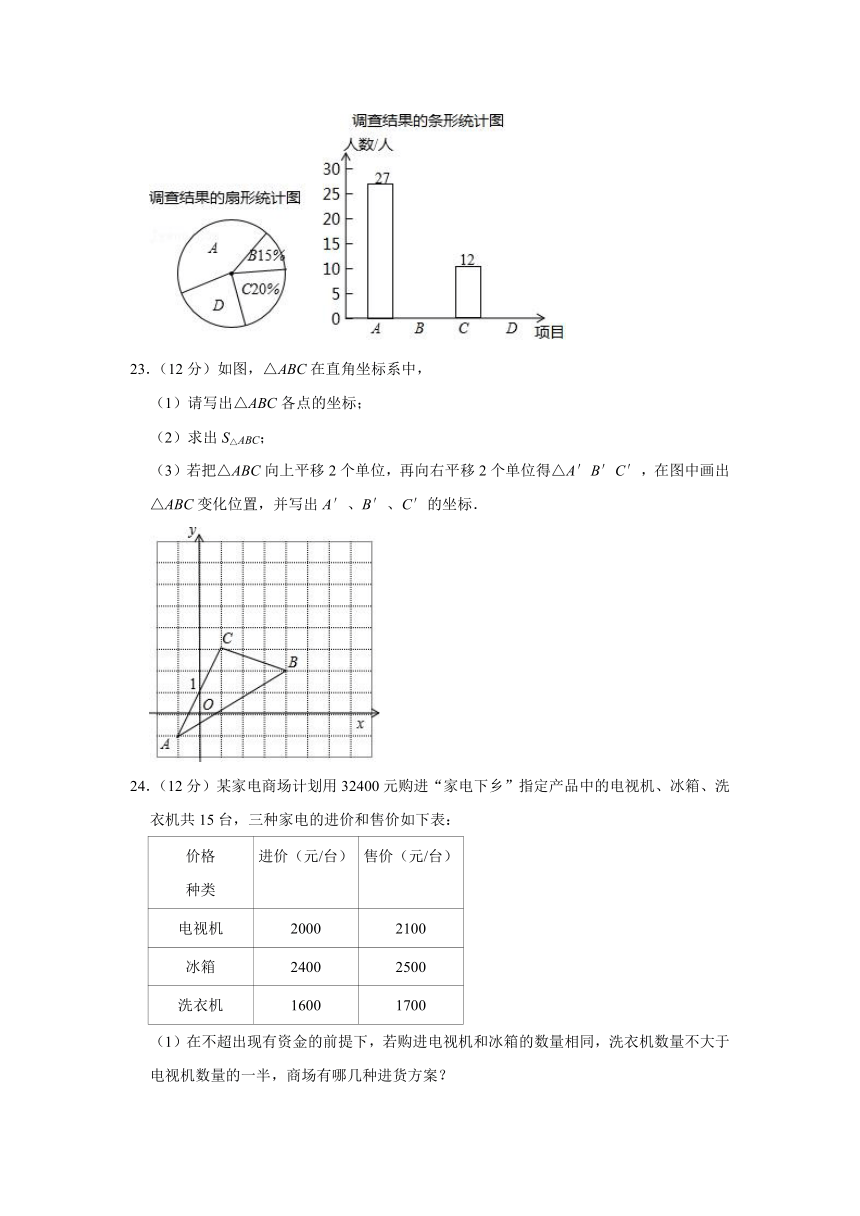
(1)如图,希望参加活动C占20%,希望参加活动B占15%,则被调查的总人数为
人,扇形统计图中,希望参加活动D所占圆心角为
度,根据题中信息补全条形统计图.
(2)学校现有800名学生,请根据图中信息,估算全校学生希望参加活动A有多少人?
23.(12分)如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标;
(2)求出S△ABC;
(3)若把△ABC向上平移2个单位,再向右平移2个单位得△A′B′C′,在图中画出△ABC变化位置,并写出A′、B′、C′的坐标.
24.(12分)某家电商场计划用32400元购进“家电下乡”指定产品中的电视机、冰箱、洗衣机共15台,三种家电的进价和售价如下表:
价格种类
进价(元/台)
售价(元/台)
电视机
2000
2100
冰箱
2400
2500
洗衣机
1600
1700
(1)在不超出现有资金的前提下,若购进电视机和冰箱的数量相同,洗衣机数量不大于电视机数量的一半,商场有哪几种进货方案?
(2)国家规定,农民购买家电后,可根据商场售价的13%领取补贴.在(1)的条件下,如果这15台家电全部销售给农民,国家最多需补贴农民多少元?
2020-2021学年河北省张家口市涿鹿县七年级(下)期末数学试卷
参考答案与试题解析
一、选择题(本大题共14个小题。每小题3分,共42分,在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.(3分)下面调查方式中,合适的是( )
A.调查你所在班级同学的身高,采用抽样调查方式
B.调查大汶河的水质情况,采用抽样调查的方式
C.调查CCTV﹣5《NBA
总决赛》栏目在我市的收视率,采用普查的方式
D.要了解全市初中学生的业余爱好,采用普查的方式
【分析】根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似判断即可.
【解答】解:A、调查你所在班级同学的身高,采用普查,故A不符合题意;
B、调查大汶河的水质情况,采用抽样调查的方式,故B符合题意;
C、调查CCTV﹣5《NBA
总决赛》栏目在我市的收视率,采用抽样调查,故C不符合题意;
D、要了解全市初中学生的业余爱好,采用抽样调查,故D不符合题意;
故选:B.
2.(3分)下列方程中是二元一次方程的是( )
A.x﹣5=3
B.x+=3
C.x+=1
D.xy=3
【分析】根据二元一次方程的定义对四个选项进行逐一分析.
【解答】解:A、含有一个未知数,是一元一次方程,故本选项错误;
B、分母中含有未知数,是分式方程,故本选项错误;
C、含有两个未知数,并且未知数的次数都是1,是二元一次方程,故本选项正确;
D、含有两个未知数,并且未知数的最高次数是2,是二元二次方程,故本选项错误.
故选:C.
3.(3分)下列说法正确的是( )
A.a,b,c是直线,且a∥b,b∥c,则a∥c
B.a,b,c是直线,且a⊥b,b⊥c,则a⊥c
C.a,b,c是直线,且a∥b,b⊥c,则a∥c
D.a,b,c是直线,且a∥b,b∥c,则a⊥c
【分析】根据“在同一平面内,如果两条直线都和第三条直线平行,那么这两条直线也互相平行”和“在同一平面内垂直于同一直线的两条直线互相平行”解答即可.
【解答】解:A、正确,根据“在同一平面内,如果两条直线都和第三条直线平行,那么这两条直线也互相平行”.
B、错误,因为“在同一平面内垂直于同一直线的两条直线互相平行”.
C、错误,a,b,c是直线,且a∥b,b⊥c则a⊥c;
D、错误,b,c是直线,且a∥b,b∥c,则a∥c.
故选:A.
4.(3分)下列说法中,错误的是( )
A.4的算术平方根是2
B.的平方根是±9
C.8的平方根是
D.平方根等于1的实数是1
【分析】根据平方根、算术平方根的定义,即可判定.
【解答】解:A、4的算术平方根是2,正确;
B、=9,9的平方根是±3,故错误;
C、8的平方根是±,正确;
D、平方根等于1的实数是1,故正确.
故选:B.
5.(3分)下列现象:①电梯的升降运动,②飞机在地面上沿直线滑行,③风车的转动,④冷水加热过程中气泡的上升.其中不属于平移的是( )
A.①②
B.①③
C.②③
D.③④
【分析】根据平移的特点可得答案.
【解答】解:①电梯的升降运动,是平移运动;
②飞机在地面上沿直线滑行,是平移运动;
③风车的转动,是旋转运动;
④冷水加热过程中气泡的上升,不是平移运动;
故选:D.
6.(3分)如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=30°,那么∠2的度数是( )
A.30°
B.50°
C.60°
D.70°
【分析】由a与b平行,利用两直线平行同位角相等得到一对角相等,再由∠ABC为直角,即可确定出所求角的度数.
【解答】解:∵a∥b,
∴∠2=∠3,
∵∠ABC=90°,
∴∠3+∠1=90°,
∴∠2+∠1=90°,
∵∠1=30°,
∴∠2=60°.
故选:C.
7.(3分)下面四个图形中,∠1与∠2是对顶角的图形为( )
A.
B.
C.
D.
【分析】根据对顶角的定义,两条直线相交后所得的只有一个公共顶点且两边互为反向延长线,这样的两个角叫做对顶角.
【解答】解:根据对顶角的定义可知:只有C选项中的是对顶角,其它都不是.
故选:C.
8.(3分)把不等式组的解集表示在数轴上,下列选项正确的是( )
A.
B.
C.
D.
【分析】本题的关键是先解不等式组,然后再在数轴上表示.
【解答】解:由(1)得x>﹣1,由(2)得x≤1,所以﹣1<x≤1.故选:B.
9.(3分)某学校的平面示意图如图所示,如果宠物店所在位置的坐标为(﹣2,﹣3),儿童公园所在位置的坐标为(﹣4,﹣2),则(0,4)所在的位置是( )
A.医院
B.学校
C.汽车站
D.水果店
【分析】根据题意,宠物店向右2个单位,向上3个单位为坐标原点建立平面直角坐标系,然后找出(0,4)所在的位置即可.
【解答】解:建立平面直角坐标系如图,
(0,4)所在的位置是学校.
故选B.
10.(3分)下列结论:
①两个无理数的和一定是无理数
②两个无理数的积一定是无理数
③任何一个无理数都能用数轴上的点表示
④实数与数轴上的点一一对应,
其中正确的是( )
A.①②
B.②③
C.③④
D.②③④
【分析】举出反例即可判断①②,根据任何有理数都能用数轴上的点表示出来即可判断③;实数和数轴上的点能建立一一对应关系,即可判断④.
【解答】解:∵如π+(﹣π)=0,0是有理数,不是无理数,∴①错误;
∵×=2,是有理数,不是无理数,∴②错误;
∵任何一个无理数都能用数轴上的点表示正确,∴③正确;
∵实数与数轴上的点一一对应,∴④正确;
故选:C.
11.(3分)甲,乙两人练习跑步,若乙先跑10米,则甲跑5秒就可以追上乙;如果乙先跑2秒,甲跑4秒就可以追上乙.设甲的速度为x米/秒,乙的速度为y米/秒,根据题意,下列选项中所列方程组正确的是( )
A.
B.
C.
D.
【分析】此题中的等量关系:①乙先跑10米,则甲跑5秒就可以追上乙;②乙先跑2秒,则甲跑4秒就可追上乙.列出方程组即可.
【解答】解:根据乙先跑10米,则甲跑5秒就可以追上乙,得方程5x﹣5y=10;
根据乙先跑2秒,则甲跑4秒就可追上乙,得方程4x=4y+2y.
可得方程组.
故选:A.
12.(3分)A、B、C是直线l上的三点,P是直线l外一点.若PA=5cm、PB=6cm、PC=8cm.由此可知,点P到直线l的距离是( )
A.5cm
B.不小于5cm
C.不大于5cm
D.在6cm与8cm之间
【分析】根据“直线外一点到直线上各点的所有线中,垂线段最短”进行解答.
【解答】解:∵直线外一点与直线上各点连接的所有线段中,垂线段最短,
∴点P到直线l的距离≤PA,
即点P到直线l的距离不大于5cm.
故选:C.
13.(3分)如图所示的运算程序中,如果开始输入的x值为﹣48,我们发现第1次输出的结果为﹣24,第2次输出的结果为﹣12,……,第2021次输出的结果为( )
A.﹣6
B.﹣3
C.﹣24
D.﹣12
【分析】根据题意和题目中的运算程序,可以写出前几次的输出结果,从而可以发现输出结果的变化规律,从而可以求得第2019次输出的结果.
【解答】解:由题意可得,
第一次输出的结果为:﹣24,
第二次输出的结果为:﹣12,
第三次输出的结果为:﹣6,
第四次输出的结果为:﹣3,
第五次输出的结果为:﹣6,
…,
∵(2021﹣2)÷2=2019÷2=1009…1,
∴第2021次输出的结果为﹣6,
故选:A.
14.(3分)利用两块长方体木块测量一张桌子的高度.首先按图1方式放置,再交换两木块的位置,按图2方式放置.测量的数据如图,则桌子的高度是( )
A.73cm
B.74cm
C.75cm
D.76cm
【分析】设长方体长xcm,宽ycm,桌子的高为acm,由图象建立方程组求出其解就可以得出结论.
【解答】解:设长方体长xcm,宽ycm,桌子的高为acm,由题意,得
,
解得:2a=152,
∴a=76.
故选:D.
二、填空题(本大题共4个小题,每小题3分,共12分)
15.(3分)同一平面内的三条直线,其交点的个数可能为 0、1、2、3 .
【分析】当三条直线平行时,没有交点,三条直线交于一点时,有一个交点;两条平行线与一条直线相交时,有两个交点;三条直线两两相交时有三个交点.画出图形,即可得到正确结果.
【解答】解:如图,同一平面内的三条直线,其交点个数为:0个;1个;2个;3个.
故答案为:0、1、2、3.
16.(3分)把7的平方根和立方根按从小到大的顺序排列为 .
【分析】先分别得到7的平方根和立方根,然后比较大小.
【解答】解:7的平方根为﹣,;7的立方根为,
所以7的平方根和立方根按从小到大的顺序排列为﹣<<.
故答案为:﹣<<.
17.(3分)已知点A(4,y),B(x,﹣3),若AB∥x轴,且线段AB的长为5,x= 9或﹣1 ,y= ﹣3 .
【分析】若AB∥x轴,则A,B的纵坐标相同,因而y=﹣3;线段AB的长为5,即|x﹣4|=5,解得x=9或﹣1.
【解答】解:若AB∥x轴,则A,B的纵坐标相同,因而y=﹣3;
线段AB的长为5,即|x﹣4|=5,解得x=9或﹣1.
故答案填:9或﹣1,﹣3.
18.(3分)若关于x的不等式组的整数解共有3个,则a的取值范围为 ﹣2<a≤﹣1 .
【分析】先把a当作已知表示出不等式组的解集,再根据不等式组有3个整数解即可求出a的取值范围.
【解答】解:,
∵由①得,x≥a;由②得,x<2,
∴不等式组的解集为:a≤x<2,
∵不等式组有3个整数解,
∴这三个整数解是:﹣1,0,1,
∴﹣2<a≤﹣1.
故答案为:﹣2<a≤﹣1.
三、解答题(本大题共6个小题,共66分,解答应写出必要的文字说明,证明过程及演算步骤)
19.(10分)解不等式组,并把它的解集在数轴上表示出来.
【分析】分别求出各不等式的解集,再求出其公共解集,并在数轴上表示出来即可.
【解答】解:,
由①得,x≥﹣2,
由②得,x<4,
故此不等式组的解集为﹣2≤x<4;
在数轴上表示为:
.
20.(10分)若方程组的解x与y是互为相反数,求k的值.
【分析】由于x与y是互为相反数,则把y=﹣x分别代入两个方程求出x,然后得到关于k的一次方程,再解此一次方程即可.
【解答】解:,
把y=﹣x代入①得x﹣2x=7+k,解得x=﹣7﹣k,
把y=﹣x代入②得5x+x=k,解得x=,
所以﹣7﹣k=,
解得k=﹣6.
21.(12分)已知,如图,∠1=∠2,∠A=∠F.求证:∠C=∠D.
证明:∵∠1=∠2(已知)
∠1=∠3( 对顶角相等
)
∴∠2=∠ 3 ( 等量代换 )
∴BD∥ CE ( 同位角相等,两直线平行 )
∴∠4=∠C
( 两直线平行,同位角相等 )
又∵∠A= ∠F (已知)
∴AC∥ DF ( 内错角相等,两直线平行 )
∴ ∠4 =∠D( 两直线平行,内错角相等 )
∴∠C=∠D( 等量代换
)
【分析】根据平行线的性质以及判定定理,结合图形即可解答.
【解答】证明:∵∠1=∠2(已知)
∠1=∠3(
对顶角相等
)
∴∠2=∠3(等量代换)
∴BD∥CE(
同位角相等,两直线平行)
∴∠4=∠C
(
两直线平行,同位角相等)
又∵∠A=∠F(已知)
∴AC∥DF(
内错角相等,两直线平行)
∴∠4=∠D(
两直线平行,内错角相等)
∴∠C=∠D(
等量代换).
22.(10分)在“弘扬传统文化,打造书香校园”活动中,学校计划开展四项活动:“A﹣国学诵读”、“B﹣演讲”、“C﹣课本剧”、“D﹣书法”,要求每位同学必须且只能参加其中一项活动,学校为了了解学生的意愿,随机调查了部分学生,结果统计如下:
(1)如图,希望参加活动C占20%,希望参加活动B占15%,则被调查的总人数为 60 人,扇形统计图中,希望参加活动D所占圆心角为 72 度,根据题中信息补全条形统计图.
(2)学校现有800名学生,请根据图中信息,估算全校学生希望参加活动A有多少人?
【分析】(1)根据统计图中希望参加C的人数和所占的百分比可以求得被调查的总人数,进而可以求得参加活动B和D的人数,计算出希望参加活动D所占圆心角的度数,将条形统计图补充完整;
(2)根据统计图中的数据可以估算全校学生希望参加活动A有多少人.
【解答】解:(1)由题意可得,
被调查的总人数是:12÷20%=60,希望参加活动B的人数为:60×15%=9,希望参加活动D的人数为:60﹣27﹣9﹣12=12,
扇形统计图中,希望参加活动D所占圆心角为:360°×(1﹣﹣15%﹣20%)=360°×20%=72°,
故答案为:60,72,
补全的条形统计图如右图所示;
(2)由题意可得,
800×=360,
答:全校学生希望参加活动A有360人.
23.(12分)如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标;
(2)求出S△ABC;
(3)若把△ABC向上平移2个单位,再向右平移2个单位得△A′B′C′,在图中画出△ABC变化位置,并写出A′、B′、C′的坐标.
【分析】(1)根据各点所在象限的符号和距坐标轴的距离可得各点的坐标;
(2)S△ABC=边长为4,5的长方形的面积减去直角边长为2,4的直角三角形的面积,减去直角边长为3,5的直角三角形的面积,减去边长为1,3的直角三角形面积;
(3)把三角形ABC的各顶点向上平移2个单位,再向右平移2个单位得到平移后的坐标,顺次连接平移后的各顶点即为平移后的三角形,根据各点所在象限的符号和距坐标轴的距离可得各点的坐标.
【解答】解:(1)A(﹣1,﹣1),B(4,2),C(1,3);
(2)S△ABC=4×5﹣×2×4﹣×1×3﹣×3×5=7;
(3)A′(1,1),B′(6,4),C′(3,5).
24.(12分)某家电商场计划用32400元购进“家电下乡”指定产品中的电视机、冰箱、洗衣机共15台,三种家电的进价和售价如下表:
价格种类
进价(元/台)
售价(元/台)
电视机
2000
2100
冰箱
2400
2500
洗衣机
1600
1700
(1)在不超出现有资金的前提下,若购进电视机和冰箱的数量相同,洗衣机数量不大于电视机数量的一半,商场有哪几种进货方案?
(2)国家规定,农民购买家电后,可根据商场售价的13%领取补贴.在(1)的条件下,如果这15台家电全部销售给农民,国家最多需补贴农民多少元?
【分析】(1)由题意可知:电视机的数量和冰箱的数量相同,则洗衣机的数量等于总台数减去2倍的电视机或洗衣机的数量,又知洗衣机数量不大于电视机数量的一半,则15﹣2x≤x;根据各个电器的单价以及数量,可列不等式2000x+2400x+1600(15﹣2x)≤32400;根据这两个不等式可以求得x的取值,根据x的取值可以确定有几种方案;
(2)分别计算出方案一和方案二的家电销售的总额,相加后将总额乘13%,即可求得补贴农民的钱数.
【解答】解:(1)1)设购进电视机、冰箱各x台,则洗衣机为(15﹣2x)台,
由题意得,
解得6≤x≤7,
∵x为整数,
∴x=6或7.
故商场有2种方案:
方案1:购进电视机、冰箱各6台、洗衣机3台.
方案2:购进电视机、冰箱各7台、洗衣机1台.
(2)设补贴为y元,则
y=[2
100x+2
500x+1
700(15﹣2x)]×13%=(1
200x+25
500)×13%,
当x=6时,y=4251;
当x=7时,y=4407.
所以国家最多需补贴农民4407元.
一、选择题(本大题共14个小题。每小题3分,共42分,在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.(3分)下面调查方式中,合适的是( )
A.调查你所在班级同学的身高,采用抽样调查方式
B.调查大汶河的水质情况,采用抽样调查的方式
C.调查CCTV﹣5《NBA
总决赛》栏目在我市的收视率,采用普查的方式
D.要了解全市初中学生的业余爱好,采用普查的方式
2.(3分)下列方程中是二元一次方程的是( )
A.x﹣5=3
B.x+=3
C.x+=1
D.xy=3
3.(3分)下列说法正确的是( )
A.a,b,c是直线,且a∥b,b∥c,则a∥c
B.a,b,c是直线,且a⊥b,b⊥c,则a⊥c
C.a,b,c是直线,且a∥b,b⊥c,则a∥c
D.a,b,c是直线,且a∥b,b∥c,则a⊥c
4.(3分)下列说法中,错误的是( )
A.4的算术平方根是2
B.的平方根是±9
C.8的平方根是
D.平方根等于1的实数是1
5.(3分)下列现象:①电梯的升降运动,②飞机在地面上沿直线滑行,③风车的转动,④冷水加热过程中气泡的上升.其中不属于平移的是( )
A.①②
B.①③
C.②③
D.③④
6.(3分)如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=30°,那么∠2的度数是( )
A.30°
B.50°
C.60°
D.70°
7.(3分)下面四个图形中,∠1与∠2是对顶角的图形为( )
A.
B.
C.
D.
8.(3分)把不等式组的解集表示在数轴上,下列选项正确的是( )
A.
B.
C.
D.
9.(3分)某学校的平面示意图如图所示,如果宠物店所在位置的坐标为(﹣2,﹣3),儿童公园所在位置的坐标为(﹣4,﹣2),则(0,4)所在的位置是( )
A.医院
B.学校
C.汽车站
D.水果店
10.(3分)下列结论:
①两个无理数的和一定是无理数
②两个无理数的积一定是无理数
③任何一个无理数都能用数轴上的点表示
④实数与数轴上的点一一对应,
其中正确的是( )
A.①②
B.②③
C.③④
D.②③④
11.(3分)甲,乙两人练习跑步,若乙先跑10米,则甲跑5秒就可以追上乙;如果乙先跑2秒,甲跑4秒就可以追上乙.设甲的速度为x米/秒,乙的速度为y米/秒,根据题意,下列选项中所列方程组正确的是( )
A.
B.
C.
D.
12.(3分)A、B、C是直线l上的三点,P是直线l外一点.若PA=5cm、PB=6cm、PC=8cm.由此可知,点P到直线l的距离是( )
A.5cm
B.不小于5cm
C.不大于5cm
D.在6cm与8cm之间
13.(3分)如图所示的运算程序中,如果开始输入的x值为﹣48,我们发现第1次输出的结果为﹣24,第2次输出的结果为﹣12,……,第2021次输出的结果为( )
A.﹣6
B.﹣3
C.﹣24
D.﹣12
14.(3分)利用两块长方体木块测量一张桌子的高度.首先按图1方式放置,再交换两木块的位置,按图2方式放置.测量的数据如图,则桌子的高度是( )
A.73cm
B.74cm
C.75cm
D.76cm
二、填空题(本大题共4个小题,每小题3分,共12分)
15.(3分)同一平面内的三条直线,其交点的个数可能为
.
16.(3分)把7的平方根和立方根按从小到大的顺序排列为
.
17.(3分)已知点A(4,y),B(x,﹣3),若AB∥x轴,且线段AB的长为5,x=
,y=
.
18.(3分)若关于x的不等式组的整数解共有3个,则a的取值范围为
.
三、解答题(本大题共6个小题,共66分,解答应写出必要的文字说明,证明过程及演算步骤)
19.(10分)解不等式组,并把它的解集在数轴上表示出来.
20.(10分)若方程组的解x与y是互为相反数,求k的值.
21.(12分)已知,如图,∠1=∠2,∠A=∠F.求证:∠C=∠D.
证明:∵∠1=∠2(已知)
∠1=∠3(
)
∴∠2=∠
(
)
∴BD∥
(
)
∴∠4=∠C
(
)
又∵∠A=
(已知)
∴AC∥
(
)
∴
=∠D(
)
∴∠C=∠D(
)
22.(10分)在“弘扬传统文化,打造书香校园”活动中,学校计划开展四项活动:“A﹣国学诵读”、“B﹣演讲”、“C﹣课本剧”、“D﹣书法”,要求每位同学必须且只能参加其中一项活动,学校为了了解学生的意愿,随机调查了部分学生,结果统计如下:
(1)如图,希望参加活动C占20%,希望参加活动B占15%,则被调查的总人数为
人,扇形统计图中,希望参加活动D所占圆心角为
度,根据题中信息补全条形统计图.
(2)学校现有800名学生,请根据图中信息,估算全校学生希望参加活动A有多少人?
23.(12分)如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标;
(2)求出S△ABC;
(3)若把△ABC向上平移2个单位,再向右平移2个单位得△A′B′C′,在图中画出△ABC变化位置,并写出A′、B′、C′的坐标.
24.(12分)某家电商场计划用32400元购进“家电下乡”指定产品中的电视机、冰箱、洗衣机共15台,三种家电的进价和售价如下表:
价格种类
进价(元/台)
售价(元/台)
电视机
2000
2100
冰箱
2400
2500
洗衣机
1600
1700
(1)在不超出现有资金的前提下,若购进电视机和冰箱的数量相同,洗衣机数量不大于电视机数量的一半,商场有哪几种进货方案?
(2)国家规定,农民购买家电后,可根据商场售价的13%领取补贴.在(1)的条件下,如果这15台家电全部销售给农民,国家最多需补贴农民多少元?
2020-2021学年河北省张家口市涿鹿县七年级(下)期末数学试卷
参考答案与试题解析
一、选择题(本大题共14个小题。每小题3分,共42分,在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.(3分)下面调查方式中,合适的是( )
A.调查你所在班级同学的身高,采用抽样调查方式
B.调查大汶河的水质情况,采用抽样调查的方式
C.调查CCTV﹣5《NBA
总决赛》栏目在我市的收视率,采用普查的方式
D.要了解全市初中学生的业余爱好,采用普查的方式
【分析】根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似判断即可.
【解答】解:A、调查你所在班级同学的身高,采用普查,故A不符合题意;
B、调查大汶河的水质情况,采用抽样调查的方式,故B符合题意;
C、调查CCTV﹣5《NBA
总决赛》栏目在我市的收视率,采用抽样调查,故C不符合题意;
D、要了解全市初中学生的业余爱好,采用抽样调查,故D不符合题意;
故选:B.
2.(3分)下列方程中是二元一次方程的是( )
A.x﹣5=3
B.x+=3
C.x+=1
D.xy=3
【分析】根据二元一次方程的定义对四个选项进行逐一分析.
【解答】解:A、含有一个未知数,是一元一次方程,故本选项错误;
B、分母中含有未知数,是分式方程,故本选项错误;
C、含有两个未知数,并且未知数的次数都是1,是二元一次方程,故本选项正确;
D、含有两个未知数,并且未知数的最高次数是2,是二元二次方程,故本选项错误.
故选:C.
3.(3分)下列说法正确的是( )
A.a,b,c是直线,且a∥b,b∥c,则a∥c
B.a,b,c是直线,且a⊥b,b⊥c,则a⊥c
C.a,b,c是直线,且a∥b,b⊥c,则a∥c
D.a,b,c是直线,且a∥b,b∥c,则a⊥c
【分析】根据“在同一平面内,如果两条直线都和第三条直线平行,那么这两条直线也互相平行”和“在同一平面内垂直于同一直线的两条直线互相平行”解答即可.
【解答】解:A、正确,根据“在同一平面内,如果两条直线都和第三条直线平行,那么这两条直线也互相平行”.
B、错误,因为“在同一平面内垂直于同一直线的两条直线互相平行”.
C、错误,a,b,c是直线,且a∥b,b⊥c则a⊥c;
D、错误,b,c是直线,且a∥b,b∥c,则a∥c.
故选:A.
4.(3分)下列说法中,错误的是( )
A.4的算术平方根是2
B.的平方根是±9
C.8的平方根是
D.平方根等于1的实数是1
【分析】根据平方根、算术平方根的定义,即可判定.
【解答】解:A、4的算术平方根是2,正确;
B、=9,9的平方根是±3,故错误;
C、8的平方根是±,正确;
D、平方根等于1的实数是1,故正确.
故选:B.
5.(3分)下列现象:①电梯的升降运动,②飞机在地面上沿直线滑行,③风车的转动,④冷水加热过程中气泡的上升.其中不属于平移的是( )
A.①②
B.①③
C.②③
D.③④
【分析】根据平移的特点可得答案.
【解答】解:①电梯的升降运动,是平移运动;
②飞机在地面上沿直线滑行,是平移运动;
③风车的转动,是旋转运动;
④冷水加热过程中气泡的上升,不是平移运动;
故选:D.
6.(3分)如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=30°,那么∠2的度数是( )
A.30°
B.50°
C.60°
D.70°
【分析】由a与b平行,利用两直线平行同位角相等得到一对角相等,再由∠ABC为直角,即可确定出所求角的度数.
【解答】解:∵a∥b,
∴∠2=∠3,
∵∠ABC=90°,
∴∠3+∠1=90°,
∴∠2+∠1=90°,
∵∠1=30°,
∴∠2=60°.
故选:C.
7.(3分)下面四个图形中,∠1与∠2是对顶角的图形为( )
A.
B.
C.
D.
【分析】根据对顶角的定义,两条直线相交后所得的只有一个公共顶点且两边互为反向延长线,这样的两个角叫做对顶角.
【解答】解:根据对顶角的定义可知:只有C选项中的是对顶角,其它都不是.
故选:C.
8.(3分)把不等式组的解集表示在数轴上,下列选项正确的是( )
A.
B.
C.
D.
【分析】本题的关键是先解不等式组,然后再在数轴上表示.
【解答】解:由(1)得x>﹣1,由(2)得x≤1,所以﹣1<x≤1.故选:B.
9.(3分)某学校的平面示意图如图所示,如果宠物店所在位置的坐标为(﹣2,﹣3),儿童公园所在位置的坐标为(﹣4,﹣2),则(0,4)所在的位置是( )
A.医院
B.学校
C.汽车站
D.水果店
【分析】根据题意,宠物店向右2个单位,向上3个单位为坐标原点建立平面直角坐标系,然后找出(0,4)所在的位置即可.
【解答】解:建立平面直角坐标系如图,
(0,4)所在的位置是学校.
故选B.
10.(3分)下列结论:
①两个无理数的和一定是无理数
②两个无理数的积一定是无理数
③任何一个无理数都能用数轴上的点表示
④实数与数轴上的点一一对应,
其中正确的是( )
A.①②
B.②③
C.③④
D.②③④
【分析】举出反例即可判断①②,根据任何有理数都能用数轴上的点表示出来即可判断③;实数和数轴上的点能建立一一对应关系,即可判断④.
【解答】解:∵如π+(﹣π)=0,0是有理数,不是无理数,∴①错误;
∵×=2,是有理数,不是无理数,∴②错误;
∵任何一个无理数都能用数轴上的点表示正确,∴③正确;
∵实数与数轴上的点一一对应,∴④正确;
故选:C.
11.(3分)甲,乙两人练习跑步,若乙先跑10米,则甲跑5秒就可以追上乙;如果乙先跑2秒,甲跑4秒就可以追上乙.设甲的速度为x米/秒,乙的速度为y米/秒,根据题意,下列选项中所列方程组正确的是( )
A.
B.
C.
D.
【分析】此题中的等量关系:①乙先跑10米,则甲跑5秒就可以追上乙;②乙先跑2秒,则甲跑4秒就可追上乙.列出方程组即可.
【解答】解:根据乙先跑10米,则甲跑5秒就可以追上乙,得方程5x﹣5y=10;
根据乙先跑2秒,则甲跑4秒就可追上乙,得方程4x=4y+2y.
可得方程组.
故选:A.
12.(3分)A、B、C是直线l上的三点,P是直线l外一点.若PA=5cm、PB=6cm、PC=8cm.由此可知,点P到直线l的距离是( )
A.5cm
B.不小于5cm
C.不大于5cm
D.在6cm与8cm之间
【分析】根据“直线外一点到直线上各点的所有线中,垂线段最短”进行解答.
【解答】解:∵直线外一点与直线上各点连接的所有线段中,垂线段最短,
∴点P到直线l的距离≤PA,
即点P到直线l的距离不大于5cm.
故选:C.
13.(3分)如图所示的运算程序中,如果开始输入的x值为﹣48,我们发现第1次输出的结果为﹣24,第2次输出的结果为﹣12,……,第2021次输出的结果为( )
A.﹣6
B.﹣3
C.﹣24
D.﹣12
【分析】根据题意和题目中的运算程序,可以写出前几次的输出结果,从而可以发现输出结果的变化规律,从而可以求得第2019次输出的结果.
【解答】解:由题意可得,
第一次输出的结果为:﹣24,
第二次输出的结果为:﹣12,
第三次输出的结果为:﹣6,
第四次输出的结果为:﹣3,
第五次输出的结果为:﹣6,
…,
∵(2021﹣2)÷2=2019÷2=1009…1,
∴第2021次输出的结果为﹣6,
故选:A.
14.(3分)利用两块长方体木块测量一张桌子的高度.首先按图1方式放置,再交换两木块的位置,按图2方式放置.测量的数据如图,则桌子的高度是( )
A.73cm
B.74cm
C.75cm
D.76cm
【分析】设长方体长xcm,宽ycm,桌子的高为acm,由图象建立方程组求出其解就可以得出结论.
【解答】解:设长方体长xcm,宽ycm,桌子的高为acm,由题意,得
,
解得:2a=152,
∴a=76.
故选:D.
二、填空题(本大题共4个小题,每小题3分,共12分)
15.(3分)同一平面内的三条直线,其交点的个数可能为 0、1、2、3 .
【分析】当三条直线平行时,没有交点,三条直线交于一点时,有一个交点;两条平行线与一条直线相交时,有两个交点;三条直线两两相交时有三个交点.画出图形,即可得到正确结果.
【解答】解:如图,同一平面内的三条直线,其交点个数为:0个;1个;2个;3个.
故答案为:0、1、2、3.
16.(3分)把7的平方根和立方根按从小到大的顺序排列为 .
【分析】先分别得到7的平方根和立方根,然后比较大小.
【解答】解:7的平方根为﹣,;7的立方根为,
所以7的平方根和立方根按从小到大的顺序排列为﹣<<.
故答案为:﹣<<.
17.(3分)已知点A(4,y),B(x,﹣3),若AB∥x轴,且线段AB的长为5,x= 9或﹣1 ,y= ﹣3 .
【分析】若AB∥x轴,则A,B的纵坐标相同,因而y=﹣3;线段AB的长为5,即|x﹣4|=5,解得x=9或﹣1.
【解答】解:若AB∥x轴,则A,B的纵坐标相同,因而y=﹣3;
线段AB的长为5,即|x﹣4|=5,解得x=9或﹣1.
故答案填:9或﹣1,﹣3.
18.(3分)若关于x的不等式组的整数解共有3个,则a的取值范围为 ﹣2<a≤﹣1 .
【分析】先把a当作已知表示出不等式组的解集,再根据不等式组有3个整数解即可求出a的取值范围.
【解答】解:,
∵由①得,x≥a;由②得,x<2,
∴不等式组的解集为:a≤x<2,
∵不等式组有3个整数解,
∴这三个整数解是:﹣1,0,1,
∴﹣2<a≤﹣1.
故答案为:﹣2<a≤﹣1.
三、解答题(本大题共6个小题,共66分,解答应写出必要的文字说明,证明过程及演算步骤)
19.(10分)解不等式组,并把它的解集在数轴上表示出来.
【分析】分别求出各不等式的解集,再求出其公共解集,并在数轴上表示出来即可.
【解答】解:,
由①得,x≥﹣2,
由②得,x<4,
故此不等式组的解集为﹣2≤x<4;
在数轴上表示为:
.
20.(10分)若方程组的解x与y是互为相反数,求k的值.
【分析】由于x与y是互为相反数,则把y=﹣x分别代入两个方程求出x,然后得到关于k的一次方程,再解此一次方程即可.
【解答】解:,
把y=﹣x代入①得x﹣2x=7+k,解得x=﹣7﹣k,
把y=﹣x代入②得5x+x=k,解得x=,
所以﹣7﹣k=,
解得k=﹣6.
21.(12分)已知,如图,∠1=∠2,∠A=∠F.求证:∠C=∠D.
证明:∵∠1=∠2(已知)
∠1=∠3( 对顶角相等
)
∴∠2=∠ 3 ( 等量代换 )
∴BD∥ CE ( 同位角相等,两直线平行 )
∴∠4=∠C
( 两直线平行,同位角相等 )
又∵∠A= ∠F (已知)
∴AC∥ DF ( 内错角相等,两直线平行 )
∴ ∠4 =∠D( 两直线平行,内错角相等 )
∴∠C=∠D( 等量代换
)
【分析】根据平行线的性质以及判定定理,结合图形即可解答.
【解答】证明:∵∠1=∠2(已知)
∠1=∠3(
对顶角相等
)
∴∠2=∠3(等量代换)
∴BD∥CE(
同位角相等,两直线平行)
∴∠4=∠C
(
两直线平行,同位角相等)
又∵∠A=∠F(已知)
∴AC∥DF(
内错角相等,两直线平行)
∴∠4=∠D(
两直线平行,内错角相等)
∴∠C=∠D(
等量代换).
22.(10分)在“弘扬传统文化,打造书香校园”活动中,学校计划开展四项活动:“A﹣国学诵读”、“B﹣演讲”、“C﹣课本剧”、“D﹣书法”,要求每位同学必须且只能参加其中一项活动,学校为了了解学生的意愿,随机调查了部分学生,结果统计如下:
(1)如图,希望参加活动C占20%,希望参加活动B占15%,则被调查的总人数为 60 人,扇形统计图中,希望参加活动D所占圆心角为 72 度,根据题中信息补全条形统计图.
(2)学校现有800名学生,请根据图中信息,估算全校学生希望参加活动A有多少人?
【分析】(1)根据统计图中希望参加C的人数和所占的百分比可以求得被调查的总人数,进而可以求得参加活动B和D的人数,计算出希望参加活动D所占圆心角的度数,将条形统计图补充完整;
(2)根据统计图中的数据可以估算全校学生希望参加活动A有多少人.
【解答】解:(1)由题意可得,
被调查的总人数是:12÷20%=60,希望参加活动B的人数为:60×15%=9,希望参加活动D的人数为:60﹣27﹣9﹣12=12,
扇形统计图中,希望参加活动D所占圆心角为:360°×(1﹣﹣15%﹣20%)=360°×20%=72°,
故答案为:60,72,
补全的条形统计图如右图所示;
(2)由题意可得,
800×=360,
答:全校学生希望参加活动A有360人.
23.(12分)如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标;
(2)求出S△ABC;
(3)若把△ABC向上平移2个单位,再向右平移2个单位得△A′B′C′,在图中画出△ABC变化位置,并写出A′、B′、C′的坐标.
【分析】(1)根据各点所在象限的符号和距坐标轴的距离可得各点的坐标;
(2)S△ABC=边长为4,5的长方形的面积减去直角边长为2,4的直角三角形的面积,减去直角边长为3,5的直角三角形的面积,减去边长为1,3的直角三角形面积;
(3)把三角形ABC的各顶点向上平移2个单位,再向右平移2个单位得到平移后的坐标,顺次连接平移后的各顶点即为平移后的三角形,根据各点所在象限的符号和距坐标轴的距离可得各点的坐标.
【解答】解:(1)A(﹣1,﹣1),B(4,2),C(1,3);
(2)S△ABC=4×5﹣×2×4﹣×1×3﹣×3×5=7;
(3)A′(1,1),B′(6,4),C′(3,5).
24.(12分)某家电商场计划用32400元购进“家电下乡”指定产品中的电视机、冰箱、洗衣机共15台,三种家电的进价和售价如下表:
价格种类
进价(元/台)
售价(元/台)
电视机
2000
2100
冰箱
2400
2500
洗衣机
1600
1700
(1)在不超出现有资金的前提下,若购进电视机和冰箱的数量相同,洗衣机数量不大于电视机数量的一半,商场有哪几种进货方案?
(2)国家规定,农民购买家电后,可根据商场售价的13%领取补贴.在(1)的条件下,如果这15台家电全部销售给农民,国家最多需补贴农民多少元?
【分析】(1)由题意可知:电视机的数量和冰箱的数量相同,则洗衣机的数量等于总台数减去2倍的电视机或洗衣机的数量,又知洗衣机数量不大于电视机数量的一半,则15﹣2x≤x;根据各个电器的单价以及数量,可列不等式2000x+2400x+1600(15﹣2x)≤32400;根据这两个不等式可以求得x的取值,根据x的取值可以确定有几种方案;
(2)分别计算出方案一和方案二的家电销售的总额,相加后将总额乘13%,即可求得补贴农民的钱数.
【解答】解:(1)1)设购进电视机、冰箱各x台,则洗衣机为(15﹣2x)台,
由题意得,
解得6≤x≤7,
∵x为整数,
∴x=6或7.
故商场有2种方案:
方案1:购进电视机、冰箱各6台、洗衣机3台.
方案2:购进电视机、冰箱各7台、洗衣机1台.
(2)设补贴为y元,则
y=[2
100x+2
500x+1
700(15﹣2x)]×13%=(1
200x+25
500)×13%,
当x=6时,y=4251;
当x=7时,y=4407.
所以国家最多需补贴农民4407元.
同课章节目录
