沪教版(上海)高一数学上册 1.3 集合的运算_3 课件(共18张PPT)
文档属性
| 名称 | 沪教版(上海)高一数学上册 1.3 集合的运算_3 课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-06 11:07:33 | ||
图片预览






文档简介
(共18张PPT)
集合之间的关系与运算
知识回顾
1.集合元素的三个特征:
确定性、互异性、无序性
2.集合的表示法:
列举法、描述法、图示法.
3.元素与集合的关系有:
∈
?
4.集合与集合之间的关系有:
包含关系
相等关系
真包含关系
?
=
5.子集与真子集
交集
A∩B=
.
并集
A∪B=
.
补集
?UA=
.
6、集合的运算
{x|x∈A且x∈B}
{x|x∈A或x∈B}
{x|x∈U且x∈A}
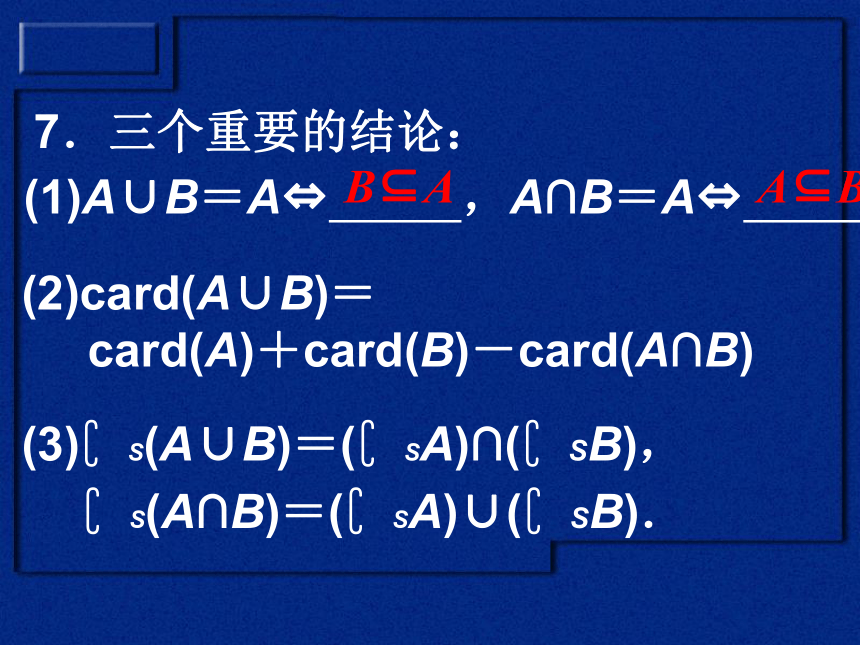
7.三个重要的结论:
(1)A∪B=A?
,A∩B=A?
.
B?A
A?B
(2)card(A∪B)=
card(A)+card(B)-card(A∩B)
(3)?S(A∪B)=(?SA)∩(?SB),
?S(A∩B)=(?SA)∪(?SB).
例题讲解
例1、有三个实数的集合既可以表
示为
,
也可以表示为
则
例2、
例3、
例4、
8
例5、某班共30人,其中15人喜爱
篮球运动,10人喜爱乒乓球运动,
8人对这两项运动都不喜爱,则喜
爱篮球运动但不喜爱乒乓球运动的
人数为________
12
例6、从集合{1,2,3,4,5}的所有非空子集中,等可能地取出一个.
(1)记性质r:集合中的所有元素之和为10,求所取出的非空子集满足性质r的概率;
(2)记所取出的非空子集的元素个数为ξ,求ξ的分布列和数学期望Eξ.
例7、
例8、
例9、
例10、
方法规律
一、集合的概念
1.解题时要注意集合中元素的三个性质的应用,特别是无序性和互异性,要进
行解题后的检验.注意符号语言与文字语言之间的相互转化.
2.解题时要关照空集的特殊地位,讨论时要防止遗漏.
3.元素与集合之间是从属关系,集合与集合之间是包含关系.
4.可以用图示显示集合与集合之间的关系,用数轴上的点表示数集,注意数形结合思想方法的运用.
二、集合的运算
1.数形结合的思想方法在集合的运
算中也是常见的,对于一般的集合运
算时可用韦恩图直观显示,对于可以
用区间表示的数集可以利用数轴进行
集合的运算.
2.注意一些常见集合运算的性质的运用.
集合之间的关系与运算
知识回顾
1.集合元素的三个特征:
确定性、互异性、无序性
2.集合的表示法:
列举法、描述法、图示法.
3.元素与集合的关系有:
∈
?
4.集合与集合之间的关系有:
包含关系
相等关系
真包含关系
?
=
5.子集与真子集
交集
A∩B=
.
并集
A∪B=
.
补集
?UA=
.
6、集合的运算
{x|x∈A且x∈B}
{x|x∈A或x∈B}
{x|x∈U且x∈A}
7.三个重要的结论:
(1)A∪B=A?
,A∩B=A?
.
B?A
A?B
(2)card(A∪B)=
card(A)+card(B)-card(A∩B)
(3)?S(A∪B)=(?SA)∩(?SB),
?S(A∩B)=(?SA)∪(?SB).
例题讲解
例1、有三个实数的集合既可以表
示为
,
也可以表示为
则
例2、
例3、
例4、
8
例5、某班共30人,其中15人喜爱
篮球运动,10人喜爱乒乓球运动,
8人对这两项运动都不喜爱,则喜
爱篮球运动但不喜爱乒乓球运动的
人数为________
12
例6、从集合{1,2,3,4,5}的所有非空子集中,等可能地取出一个.
(1)记性质r:集合中的所有元素之和为10,求所取出的非空子集满足性质r的概率;
(2)记所取出的非空子集的元素个数为ξ,求ξ的分布列和数学期望Eξ.
例7、
例8、
例9、
例10、
方法规律
一、集合的概念
1.解题时要注意集合中元素的三个性质的应用,特别是无序性和互异性,要进
行解题后的检验.注意符号语言与文字语言之间的相互转化.
2.解题时要关照空集的特殊地位,讨论时要防止遗漏.
3.元素与集合之间是从属关系,集合与集合之间是包含关系.
4.可以用图示显示集合与集合之间的关系,用数轴上的点表示数集,注意数形结合思想方法的运用.
二、集合的运算
1.数形结合的思想方法在集合的运
算中也是常见的,对于一般的集合运
算时可用韦恩图直观显示,对于可以
用区间表示的数集可以利用数轴进行
集合的运算.
2.注意一些常见集合运算的性质的运用.
