沪教版(上海)高一数学上册 4.3 借助计算器观察函数递增的快慢 课件(共20张PPT)
文档属性
| 名称 | 沪教版(上海)高一数学上册 4.3 借助计算器观察函数递增的快慢 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 346.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-06 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
借助计算器观察函数递增的快慢
我们以实例展开研究
幂函数
、指数函数
和线性函数
在区间
上都是单调增函数,增函数递增的快慢是单调函数的重要性质。
用描点法作出它们的图象:
解:首先建立模型
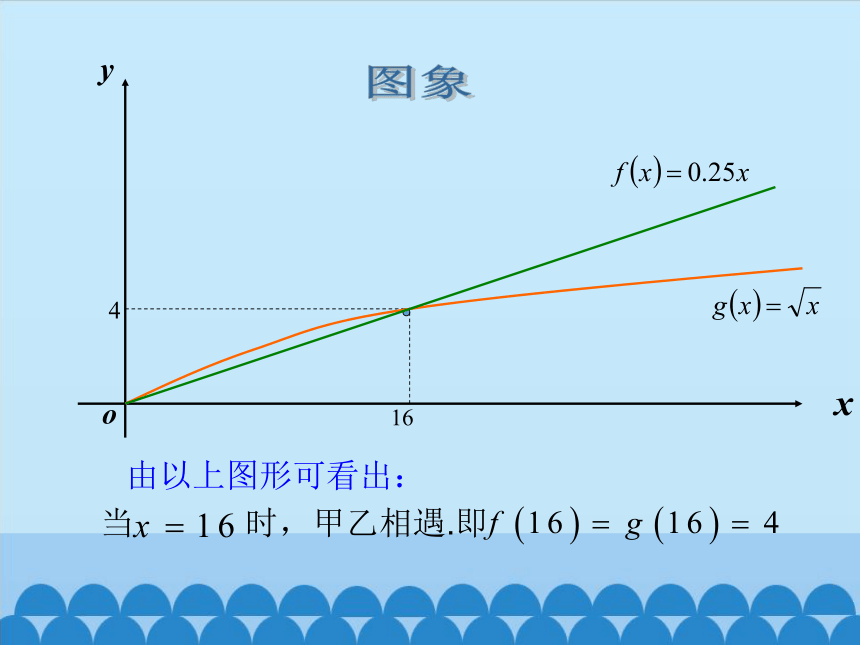
由以上图形可看出:
图象
当
时,甲乙相遇.即
仔细观察两个函数的图像关系,可以得出以下事实:
甲乙两兔同时出发,乙兔的速度快于甲兔的速度,乙兔跑在甲兔前面且超前距离越来越大
经过一段时间后,乙兔的速度逐渐减慢,乙兔超前距离逐渐缩小
乙兔被甲兔追上,甲乙两兔相遇
乙兔的速度在减慢,乙兔落后于甲兔,最终甲兔跑在乙兔的前面且超前距离越来越大
甲兔的速度保持不变,乙兔的速度一直变化
注意:
函数图像上下方位置反映的是甲乙两兔所跑路程的长短,不能反映速度的快慢;两个函数图像上下方的分界点与函数值递增快慢的分界点不一定是同一个点.
思考:无法从函数的图像上发现任意时刻谁的速度大.那么,如何分析和描述甲乙两兔的速度变化关系呢?
平均变化率概念与模型的构建
为了刻画函数变化的快慢,定义
为平均变化率.它刻画了函数
在
到
上的增长快慢
特别地,当
时
,有
下面我们研究甲乙两兔递增速度的快慢比较
在赛跑过程中,甲兔保持0.25米/秒的匀速运动,而通过计算可知乙兔在[0,1),[1,2),[2,3),[3,4)各区间段内的平均速度均大于0.25,而在[4,5)以后各区间段内的平均速度均小于0.25
因此,可以得到,在
内甲兔慢于乙兔,而在
内甲兔快于乙兔。
如果时间区间
取得更小些,会得出相同的结果吗?
小结
利用平均变化率
这个数学模型描述函数递增的快慢.这是在
、
的起始点相同,且区间相同的前提下进行的函数递增快慢的比较,这是一种局部性质的讨论.事实上,平均变化率反映了函数局部变化快慢的性质.
试一试
在同一坐标系观察函数
和
在
上的图象,说明在不同区间内函数增长的快慢.
增加量
增加量
0
0
/
0
/
1
6
6
1
1
2
12
6
4
3
3
18
6
9
5
4
24
6
16
7
5
30
6
25
9
6
36
6
36
11
7
42
6
49
13
总结规律:
幂函数与线性函数的比较:当幂函数
当
,
适当增大时,幂函数增长慢于线性函数递增;当
,
适当增大时,幂函数递增快于线性递增.
巩固与拓展
x
x2
x3
1.1x
1.2x
0
1
30
50
100
150
200
250
300
350
400
x
x2
x3
1.1x
1.2x
0
0
0
1
1
1
30
50
100
150
200
250
300
350
400
x
x2
x3
1.1x
1.2x
0
0
0
1
1
1
1
1
1.1
1.2
30
50
100
150
200
250
300
350
400
x
x2
x3
1.1x
1.2x
0
0
0
1
1
1
1
1
1.1
1.2
30
900
27000
17.4494
237.3763
50
100
150
200
250
300
350
400
x
x2
x3
1.1x
1.2x
0
0
0
1
1
1
1
1
1.1
1.2
30
900
27000
17.4494
237.3763
50
2500
125000
117.391
9100.4382
100
150
200
250
300
350
400
x
x2
x3
1.1x
1.2x
0
1
30
50
100
10000
1000000
13780.612
82817974.52
150
200
250
300
350
400
x
x2
x3
1.1x
1.2x
0
1
30
50
100
150
22500
3375000
1617717.836
7.5368×1011
200
250
300
350
400
x
x2
x3
1.1x
1.2x
0
1
30
50
100
150
200
40000
8000000
189905276.5
6.8588×1015
250
300
350
400
x
x2
x3
1.1x
1.2x
0
1
30
50
100
150
200
250
62500
15625000
2.23×1010
6.242×1019
300
350
400
x
x2
x3
1.1x
1.2x
0
1
30
50
100
150
200
250
300
90000
27000000
2.617×1012
5.68×1023
350
400
x
x2
x3
1.1x
1.2x
0
1
30
50
100
150
200
250
300
350
122500
42875000
3.072×1014
5.17×1027
400
x
x2
x3
1.1x
1.2x
0
1
30
50
100
150
200
250
300
350
400
160000
64000000
3.61×1016
4.7×1031
从表中数值变化的观察可以归纳哪些函数递增的规律?
思考:
由以上分析可得出哪些规律?
总结规律:
指数函数与幂函数、线性函数的比较:当
适当大时,指数函数(底数
)递增快于幂函数和线性函数的递增。
谢
谢!
借助计算器观察函数递增的快慢
我们以实例展开研究
幂函数
、指数函数
和线性函数
在区间
上都是单调增函数,增函数递增的快慢是单调函数的重要性质。
用描点法作出它们的图象:
解:首先建立模型
由以上图形可看出:
图象
当
时,甲乙相遇.即
仔细观察两个函数的图像关系,可以得出以下事实:
甲乙两兔同时出发,乙兔的速度快于甲兔的速度,乙兔跑在甲兔前面且超前距离越来越大
经过一段时间后,乙兔的速度逐渐减慢,乙兔超前距离逐渐缩小
乙兔被甲兔追上,甲乙两兔相遇
乙兔的速度在减慢,乙兔落后于甲兔,最终甲兔跑在乙兔的前面且超前距离越来越大
甲兔的速度保持不变,乙兔的速度一直变化
注意:
函数图像上下方位置反映的是甲乙两兔所跑路程的长短,不能反映速度的快慢;两个函数图像上下方的分界点与函数值递增快慢的分界点不一定是同一个点.
思考:无法从函数的图像上发现任意时刻谁的速度大.那么,如何分析和描述甲乙两兔的速度变化关系呢?
平均变化率概念与模型的构建
为了刻画函数变化的快慢,定义
为平均变化率.它刻画了函数
在
到
上的增长快慢
特别地,当
时
,有
下面我们研究甲乙两兔递增速度的快慢比较
在赛跑过程中,甲兔保持0.25米/秒的匀速运动,而通过计算可知乙兔在[0,1),[1,2),[2,3),[3,4)各区间段内的平均速度均大于0.25,而在[4,5)以后各区间段内的平均速度均小于0.25
因此,可以得到,在
内甲兔慢于乙兔,而在
内甲兔快于乙兔。
如果时间区间
取得更小些,会得出相同的结果吗?
小结
利用平均变化率
这个数学模型描述函数递增的快慢.这是在
、
的起始点相同,且区间相同的前提下进行的函数递增快慢的比较,这是一种局部性质的讨论.事实上,平均变化率反映了函数局部变化快慢的性质.
试一试
在同一坐标系观察函数
和
在
上的图象,说明在不同区间内函数增长的快慢.
增加量
增加量
0
0
/
0
/
1
6
6
1
1
2
12
6
4
3
3
18
6
9
5
4
24
6
16
7
5
30
6
25
9
6
36
6
36
11
7
42
6
49
13
总结规律:
幂函数与线性函数的比较:当幂函数
当
,
适当增大时,幂函数增长慢于线性函数递增;当
,
适当增大时,幂函数递增快于线性递增.
巩固与拓展
x
x2
x3
1.1x
1.2x
0
1
30
50
100
150
200
250
300
350
400
x
x2
x3
1.1x
1.2x
0
0
0
1
1
1
30
50
100
150
200
250
300
350
400
x
x2
x3
1.1x
1.2x
0
0
0
1
1
1
1
1
1.1
1.2
30
50
100
150
200
250
300
350
400
x
x2
x3
1.1x
1.2x
0
0
0
1
1
1
1
1
1.1
1.2
30
900
27000
17.4494
237.3763
50
100
150
200
250
300
350
400
x
x2
x3
1.1x
1.2x
0
0
0
1
1
1
1
1
1.1
1.2
30
900
27000
17.4494
237.3763
50
2500
125000
117.391
9100.4382
100
150
200
250
300
350
400
x
x2
x3
1.1x
1.2x
0
1
30
50
100
10000
1000000
13780.612
82817974.52
150
200
250
300
350
400
x
x2
x3
1.1x
1.2x
0
1
30
50
100
150
22500
3375000
1617717.836
7.5368×1011
200
250
300
350
400
x
x2
x3
1.1x
1.2x
0
1
30
50
100
150
200
40000
8000000
189905276.5
6.8588×1015
250
300
350
400
x
x2
x3
1.1x
1.2x
0
1
30
50
100
150
200
250
62500
15625000
2.23×1010
6.242×1019
300
350
400
x
x2
x3
1.1x
1.2x
0
1
30
50
100
150
200
250
300
90000
27000000
2.617×1012
5.68×1023
350
400
x
x2
x3
1.1x
1.2x
0
1
30
50
100
150
200
250
300
350
122500
42875000
3.072×1014
5.17×1027
400
x
x2
x3
1.1x
1.2x
0
1
30
50
100
150
200
250
300
350
400
160000
64000000
3.61×1016
4.7×1031
从表中数值变化的观察可以归纳哪些函数递增的规律?
思考:
由以上分析可得出哪些规律?
总结规律:
指数函数与幂函数、线性函数的比较:当
适当大时,指数函数(底数
)递增快于幂函数和线性函数的递增。
谢
谢!
