沪教版(上海)高一数学上册 2.2 一元二次不等式的解法_3 课件(共36张PPT)
文档属性
| 名称 | 沪教版(上海)高一数学上册 2.2 一元二次不等式的解法_3 课件(共36张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-06 00:00:00 | ||
图片预览











文档简介
(共36张PPT)
一元二次不等式
一元二次不等式的解法
1.会从实际情境中抽象出一元二次不等式模型.
2.通过函数图像了解一元二次不等式与相应二次函数、一元二次方程的联系.
3.会解一元二次不等式,对给定的一元二次不等式,会设计求解的程序框图.
1.对一元二次不等式解法和三个“二次”关系的考查是本节热点.
2.本节内容常与二次函数图像、一元二次方程、集合等内容结合命题.
3.多以选择题、填空题形式考查.
1.已知二次函数f(x)的两个零点分别为x1、x2
则f(x)=
.
2.一元二次方程ax2+bx+c=0(a≠0)
当Δ<0时,
实数根;当Δ=0时,有
实数根x=
;当Δ>0时,有
实数根x=
.
3.若y=x2-2x-3,则当x∈
时,y=0;当x∈
时,y>0;当x∈
时,y<0.
a(x-x1)(x-x2)(a≠0)
没有
两个相等
两个不等
{-1,3}
(-∞,-1)∪(3,+∞)
(-1,3)
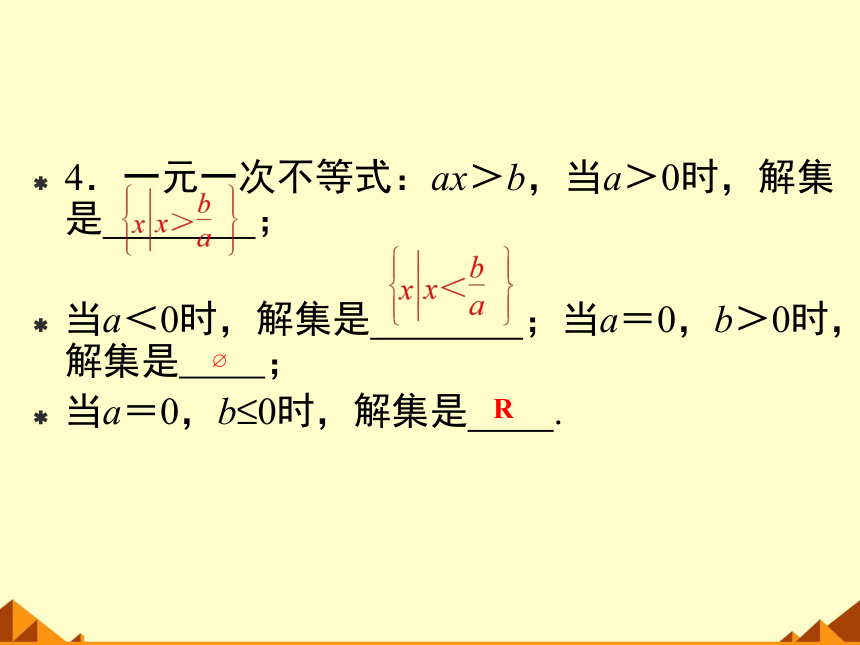
4.一元一次不等式:ax>b,当a>0时,解集是
;
当a<0时,解集是
;当a=0,b>0时,解集是
;
当a=0,b≤0时,解集是
.
?
R
1.一元二次不等式
一般地,含有
未知数,且未知数的最高次数为
的不等式,叫做一元二次不等式.
使某个一元二次不等式
叫这个一元二次不等式的解.
一元二次不等式的
组成的集合,叫做这个一元二次不等式的解集.
一个
二次
成立的x的值
所有解
2.二次函数、二次方程、二次不等式间的关系
1.下列不等式中一元二次不等式的个数为( )
①(m+1)x2-3x+1<0;②2x2-x>2;
③-x2+5x+6≥0;④(x+a)(x+a+1)<0.
A.1
B.2
C.3
D.4
解析: ③④符合一元二次不等式的定义;对于①,当m+1=0时,不是一元二次不等式;而②是指数不等式.
答案: B
2.不等式(x-2)(x+3)>0的解集是( )
A.(-3,2)
B.(2,+∞)
C.(-∞,-3)∪(2,+∞)
D.(-∞,-2)∪(3,+∞)
解析: 不等式(x-2)(x+3)>0的解集是(-∞,-3)∪(2,+∞),故选C.
答案: C
3.若集合A={x|(2x+1)(x-3)<0},B={x∈N+|x≤5},则A∩B=________.
答案: {1,2}
4.函数y=x2+4x-5的判别式Δ________0,该图像与x轴有________个交点,其交点横坐标为________,不等式x2+4x-5>0的解集是________,不等式x2+4x-5<0的解集是________.
答案: > 两 -5 1 (-∞,-5)∪(1,+∞)
(-5,1)
5.解下列不等式:
(1)x2+2x-15>0;(2)x2>2x-1;(3)x2<2x-2.
解析: (1)x2+2x-15>0?(x+5)(x-3)>0?x<-5或x>3,
∴不等式的解集是{x|x<-5或x>3}.
(2)x2>2x-1?x2-2x+1>0?(x-1)2>0?x≠1,
∴不等式的解集是{x∈R|x≠1}.
(3)x2<2x-2?x2-2x+2<0.
∵Δ=(-2)2-4×2=-4<0,
∴方程x2-2x+2=0无解.
∴不等式x2<2x-2的解集是?.
由题目可以获取以下主要信息:
①(1)、(2)题二次项系数为正,(3)、(4)二次项系数为负.
②(1)、(3)题对应方程的判别式大于零.(2)、(4)题对应方程的判别式等于零.
解答本题可先将二次项系数化为正,再求对应方程的根,并根据根的情况画出草图,观察图像写出解集.
(3)由-x2+7x>6,得x2-7x+6<0,
而x2-7x+6=0的两个根是x=1或x=6.
∴不等式x2-7x+6<0的解集为{x|1(4)原不等式可化为x2-6x+9<0,即(x-3)2<0,
∴原不等式的解集为?.
[题后感悟] 解不含参数的一元二次不等式的一般步骤:
(1)通过对不等式的变形,使不等式右侧为0,使二次项系数为正.
(2)对不等式左侧因式分解,若不易分解,则计算对应方程的判别式.
(3)求出相应的一元二次方程的根或根据判别式说明方程无实根.
(4)根据一元二次方程根的情况画出对应的二次函数的草图.
(5)根据图像写出不等式的解集.
1.求下列不等式的解集.
(1)-2x2+3x+2<0;(2)-2x2+x-6<0;
(3)4x2+4x+1>0;(4)x2+25≤10x.
解关于x的不等式:ax2-(a-1)x-1<0(a∈R).
[策略点睛]
[题后感悟] 对字母系数分类讨论时,要注意确定分类的标准,而且分类时要不重不漏.一般方法是:
(1)当二次项系数不确定时,按二次项系数等于零、大于零、小于零三种情况进行分类.
(2)判别式大于零时,还需要讨论两根的大小.
(3)判别式不确定时,按判别式大于零、等于零、小于零三种情况讨论.
解关于x的不等式:ax2-2(a+1)x+4>0.
若不等式ax2+bx+c>0的解集为{x|-3根据已知解集和一元二次不等式解的结构,逆向推出a、b、c应满足的关系,进而求解不等式.一元二次不等式解集的两个端点值是一元二次方程的两根.
两边同除以-a>0,即x2-2x-15<0,
令x2-2x-15=0,则Δ=64>0,且x1=-3,x2=5是方程的两个根,
故所求的不等式的解集为{x|-3[题后感悟] 解一元二次不等式要密切联系其所对应的一元二次方程以及二次函数的图像.一元二次方程的根就是二次函数图像与x轴交点的横坐标,对应不等式的解集,就是使函数图像在x轴上方或下方的部分所对应的x的集合,而方程的根就是不等式解集区间的端点.
已知关于x的不等式x2+ax+b<0的解集为(1,2),试求关于x的不等式bx2+ax+1>0的解集.
1.解一元二次不等式解集的一般步骤
(1)化一元二次不等式为标准形式:ax2+bx+c>0或ax2+bx+c<0(a>0);
(2)求出一元二次方程ax2+bx+c=0(a>0)的根,并画出对应函数y=ax2+bx+c(a>0)的简图;
(3)根据图像写出不等式的解集.
当一元二次不等式为ax2+bx+c≥0或ax2+bx+c≤0时,要注意解集的端点.
2.求解一般的一元二次不等式ax2+bx+c>0(a>0)的解集过程可用如下程序框图表示.
◎解不等式x2>x.
【错解】 由x2>x两边同时约去x,得x>1,
所以原不等式的解集为{x|x>1}.
【错因】 本题因没有将不等式化成标准形式,直接约去x而现求解错误.应将一元二次不等式化成标准形式,再由方程的根得出解集.
【正解】 原不等式可化为x2-x>0,
即x(x-1)>0.
∵方程x(x-1)=0的两根为x1=0,x2=1
∴原不等式的解集为{x|x>1或x<0}.
一元二次不等式
一元二次不等式的解法
1.会从实际情境中抽象出一元二次不等式模型.
2.通过函数图像了解一元二次不等式与相应二次函数、一元二次方程的联系.
3.会解一元二次不等式,对给定的一元二次不等式,会设计求解的程序框图.
1.对一元二次不等式解法和三个“二次”关系的考查是本节热点.
2.本节内容常与二次函数图像、一元二次方程、集合等内容结合命题.
3.多以选择题、填空题形式考查.
1.已知二次函数f(x)的两个零点分别为x1、x2
则f(x)=
.
2.一元二次方程ax2+bx+c=0(a≠0)
当Δ<0时,
实数根;当Δ=0时,有
实数根x=
;当Δ>0时,有
实数根x=
.
3.若y=x2-2x-3,则当x∈
时,y=0;当x∈
时,y>0;当x∈
时,y<0.
a(x-x1)(x-x2)(a≠0)
没有
两个相等
两个不等
{-1,3}
(-∞,-1)∪(3,+∞)
(-1,3)
4.一元一次不等式:ax>b,当a>0时,解集是
;
当a<0时,解集是
;当a=0,b>0时,解集是
;
当a=0,b≤0时,解集是
.
?
R
1.一元二次不等式
一般地,含有
未知数,且未知数的最高次数为
的不等式,叫做一元二次不等式.
使某个一元二次不等式
叫这个一元二次不等式的解.
一元二次不等式的
组成的集合,叫做这个一元二次不等式的解集.
一个
二次
成立的x的值
所有解
2.二次函数、二次方程、二次不等式间的关系
1.下列不等式中一元二次不等式的个数为( )
①(m+1)x2-3x+1<0;②2x2-x>2;
③-x2+5x+6≥0;④(x+a)(x+a+1)<0.
A.1
B.2
C.3
D.4
解析: ③④符合一元二次不等式的定义;对于①,当m+1=0时,不是一元二次不等式;而②是指数不等式.
答案: B
2.不等式(x-2)(x+3)>0的解集是( )
A.(-3,2)
B.(2,+∞)
C.(-∞,-3)∪(2,+∞)
D.(-∞,-2)∪(3,+∞)
解析: 不等式(x-2)(x+3)>0的解集是(-∞,-3)∪(2,+∞),故选C.
答案: C
3.若集合A={x|(2x+1)(x-3)<0},B={x∈N+|x≤5},则A∩B=________.
答案: {1,2}
4.函数y=x2+4x-5的判别式Δ________0,该图像与x轴有________个交点,其交点横坐标为________,不等式x2+4x-5>0的解集是________,不等式x2+4x-5<0的解集是________.
答案: > 两 -5 1 (-∞,-5)∪(1,+∞)
(-5,1)
5.解下列不等式:
(1)x2+2x-15>0;(2)x2>2x-1;(3)x2<2x-2.
解析: (1)x2+2x-15>0?(x+5)(x-3)>0?x<-5或x>3,
∴不等式的解集是{x|x<-5或x>3}.
(2)x2>2x-1?x2-2x+1>0?(x-1)2>0?x≠1,
∴不等式的解集是{x∈R|x≠1}.
(3)x2<2x-2?x2-2x+2<0.
∵Δ=(-2)2-4×2=-4<0,
∴方程x2-2x+2=0无解.
∴不等式x2<2x-2的解集是?.
由题目可以获取以下主要信息:
①(1)、(2)题二次项系数为正,(3)、(4)二次项系数为负.
②(1)、(3)题对应方程的判别式大于零.(2)、(4)题对应方程的判别式等于零.
解答本题可先将二次项系数化为正,再求对应方程的根,并根据根的情况画出草图,观察图像写出解集.
(3)由-x2+7x>6,得x2-7x+6<0,
而x2-7x+6=0的两个根是x=1或x=6.
∴不等式x2-7x+6<0的解集为{x|1
∴原不等式的解集为?.
[题后感悟] 解不含参数的一元二次不等式的一般步骤:
(1)通过对不等式的变形,使不等式右侧为0,使二次项系数为正.
(2)对不等式左侧因式分解,若不易分解,则计算对应方程的判别式.
(3)求出相应的一元二次方程的根或根据判别式说明方程无实根.
(4)根据一元二次方程根的情况画出对应的二次函数的草图.
(5)根据图像写出不等式的解集.
1.求下列不等式的解集.
(1)-2x2+3x+2<0;(2)-2x2+x-6<0;
(3)4x2+4x+1>0;(4)x2+25≤10x.
解关于x的不等式:ax2-(a-1)x-1<0(a∈R).
[策略点睛]
[题后感悟] 对字母系数分类讨论时,要注意确定分类的标准,而且分类时要不重不漏.一般方法是:
(1)当二次项系数不确定时,按二次项系数等于零、大于零、小于零三种情况进行分类.
(2)判别式大于零时,还需要讨论两根的大小.
(3)判别式不确定时,按判别式大于零、等于零、小于零三种情况讨论.
解关于x的不等式:ax2-2(a+1)x+4>0.
若不等式ax2+bx+c>0的解集为{x|-3
两边同除以-a>0,即x2-2x-15<0,
令x2-2x-15=0,则Δ=64>0,且x1=-3,x2=5是方程的两个根,
故所求的不等式的解集为{x|-3
已知关于x的不等式x2+ax+b<0的解集为(1,2),试求关于x的不等式bx2+ax+1>0的解集.
1.解一元二次不等式解集的一般步骤
(1)化一元二次不等式为标准形式:ax2+bx+c>0或ax2+bx+c<0(a>0);
(2)求出一元二次方程ax2+bx+c=0(a>0)的根,并画出对应函数y=ax2+bx+c(a>0)的简图;
(3)根据图像写出不等式的解集.
当一元二次不等式为ax2+bx+c≥0或ax2+bx+c≤0时,要注意解集的端点.
2.求解一般的一元二次不等式ax2+bx+c>0(a>0)的解集过程可用如下程序框图表示.
◎解不等式x2>x.
【错解】 由x2>x两边同时约去x,得x>1,
所以原不等式的解集为{x|x>1}.
【错因】 本题因没有将不等式化成标准形式,直接约去x而现求解错误.应将一元二次不等式化成标准形式,再由方程的根得出解集.
【正解】 原不等式可化为x2-x>0,
即x(x-1)>0.
∵方程x(x-1)=0的两根为x1=0,x2=1
∴原不等式的解集为{x|x>1或x<0}.
