沪教版(上海)高一数学上册 第4章 幂函数、指数函数和对数函数(上) 复习 课件(共18张PPT)
文档属性
| 名称 | 沪教版(上海)高一数学上册 第4章 幂函数、指数函数和对数函数(上) 复习 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 495.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-06 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
第4章
幂函数、指数函数和对数函数(上)
复习课件
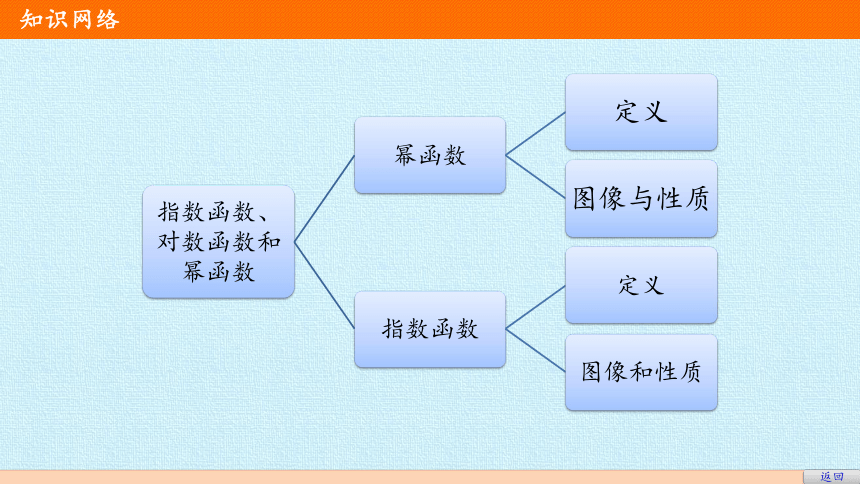
一、知识网络
整体构建
二、要点归纳
主干梳理
三、题型探究
重点突破
栏目索引
返回
知识网络
(1)所有的幂函数在(0,+∞)上都有定义,并且图象都过点(1,1);
(2)如果α>0,则幂函数的图象过原点,并且在区间[0,+∞)上为增函数;
(3)如果α<0,则幂函数的图象在区间(0,+∞)上是减函数,在第一象限内,当x从右边趋向于原点时,图象在y轴右方无限地逼近y轴,当x从原点趋向于+∞时,图象在x轴上方无限地逼近x轴;
(4)当α为奇数时,幂函数为奇函数;当α为偶数时,幂函数为偶函数.
知识点一 幂函数y=xα的性质
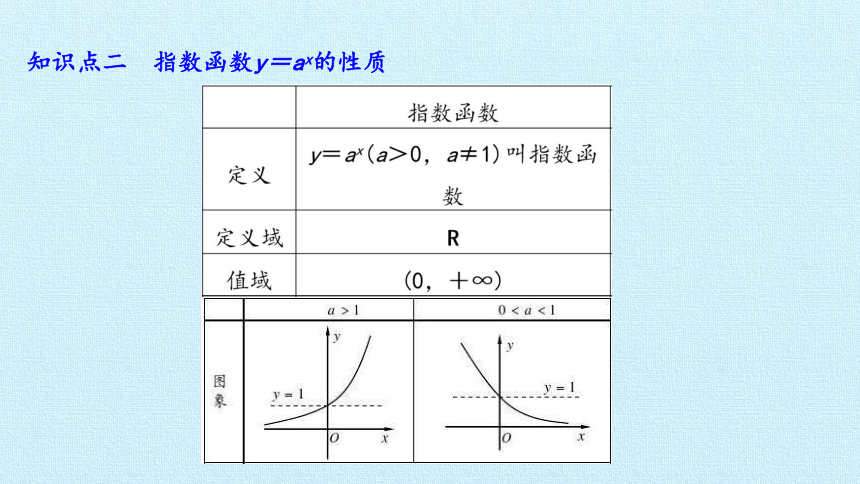
知识点二 指数函数y=ax的性质
知识点二 指数函数y=ax的性质
.
题型一 有关指数的运算问题
指数与指数运算是本章重要的知识点,不仅是本章考查的重要题型,也是高考的必考内容.
指数式的运算首先要注意化简顺序,一般负指数先转化成正指数,根式化为指数式;其次若出现分式,则要注意把分子、分母因式分解以达到约分的目的.
题型探究
解析答案
题型二 指数函数、幂函数的图象与性质
函数的图象是研究函数性质的前提和基础,它较形象直观地反映了函数的一切性质。教材对幂函数和指数函数的性质的研究也正好体现了由图象到性质,由具体到抽象的过程,突出了函数图象在研究相应函数性质时的作用.
解析答案
(1)画出函数f(x)的图象;
解析答案
(2)根据图象写出f(x)的单调区间,并写出函数的值域.
解 函数f(x)的单调递增区间为(-∞,0),单调递减区间为[0,+∞),值域为(0,1].
题型三 比较大小
比较几个数的大小问题是指数函数、幂函数的重要应用,其基本方法是:将需要比较大小的几个数视为某类函数的函数值,其主要方法可分以下三种:
(1)根据函数的单调性(如根据一次函数、二次函数、指数函数、幂函数的单调性),利用单调性的定义求解;
(2)采用中间量的方法(实际上也要用到函数的单调性),常用的中间量如0,1,-1等;
(3)采用数形结合的方法,通过函数的图象解决.
解析答案
a<b
数形结合思想
解决思想方法
在解数学问题时,将抽象的数学语言与直观的图形结合起来,就是使抽象思维和形象思维联系在一起,实现抽象概念与具体图象之间的相互转化,即数量关系转化为图形的性质或者把图形的性质转化为数量关系来研究.
解析答案
解析 易知函数f(x)的图象如图所示:
由图可知00转化与化归思想
解决思想方法
转化是将数学命题由一种形式转向另一种形式的转换过程;化归是将待解决的问题通过某种转化的过程,归结为一类已解决或比较容易解决的问题.在解决函数问题时,常进行数与形或数与数的转化,从而达到解决问题的目的.
例5 当a为何值时,函数y=7x2-(a+13)x+a2-a-2的一个零点在区间(0,1)上,另一个零点在区间(1,2)上.
解 已知函数对应的方程为7x2-(a+13)x+a2-a-2=0,
函数的大致图象如图所示.
根据方程的根与函数的零点的关系,
方程的根一个在(0,1)上,另一个在(1,2)上,
∴-2<a<-1或3<a<4.
返回
解析答案
谢
谢
第4章
幂函数、指数函数和对数函数(上)
复习课件
一、知识网络
整体构建
二、要点归纳
主干梳理
三、题型探究
重点突破
栏目索引
返回
知识网络
(1)所有的幂函数在(0,+∞)上都有定义,并且图象都过点(1,1);
(2)如果α>0,则幂函数的图象过原点,并且在区间[0,+∞)上为增函数;
(3)如果α<0,则幂函数的图象在区间(0,+∞)上是减函数,在第一象限内,当x从右边趋向于原点时,图象在y轴右方无限地逼近y轴,当x从原点趋向于+∞时,图象在x轴上方无限地逼近x轴;
(4)当α为奇数时,幂函数为奇函数;当α为偶数时,幂函数为偶函数.
知识点一 幂函数y=xα的性质
知识点二 指数函数y=ax的性质
知识点二 指数函数y=ax的性质
.
题型一 有关指数的运算问题
指数与指数运算是本章重要的知识点,不仅是本章考查的重要题型,也是高考的必考内容.
指数式的运算首先要注意化简顺序,一般负指数先转化成正指数,根式化为指数式;其次若出现分式,则要注意把分子、分母因式分解以达到约分的目的.
题型探究
解析答案
题型二 指数函数、幂函数的图象与性质
函数的图象是研究函数性质的前提和基础,它较形象直观地反映了函数的一切性质。教材对幂函数和指数函数的性质的研究也正好体现了由图象到性质,由具体到抽象的过程,突出了函数图象在研究相应函数性质时的作用.
解析答案
(1)画出函数f(x)的图象;
解析答案
(2)根据图象写出f(x)的单调区间,并写出函数的值域.
解 函数f(x)的单调递增区间为(-∞,0),单调递减区间为[0,+∞),值域为(0,1].
题型三 比较大小
比较几个数的大小问题是指数函数、幂函数的重要应用,其基本方法是:将需要比较大小的几个数视为某类函数的函数值,其主要方法可分以下三种:
(1)根据函数的单调性(如根据一次函数、二次函数、指数函数、幂函数的单调性),利用单调性的定义求解;
(2)采用中间量的方法(实际上也要用到函数的单调性),常用的中间量如0,1,-1等;
(3)采用数形结合的方法,通过函数的图象解决.
解析答案
a<b
数形结合思想
解决思想方法
在解数学问题时,将抽象的数学语言与直观的图形结合起来,就是使抽象思维和形象思维联系在一起,实现抽象概念与具体图象之间的相互转化,即数量关系转化为图形的性质或者把图形的性质转化为数量关系来研究.
解析答案
解析 易知函数f(x)的图象如图所示:
由图可知0
解决思想方法
转化是将数学命题由一种形式转向另一种形式的转换过程;化归是将待解决的问题通过某种转化的过程,归结为一类已解决或比较容易解决的问题.在解决函数问题时,常进行数与形或数与数的转化,从而达到解决问题的目的.
例5 当a为何值时,函数y=7x2-(a+13)x+a2-a-2的一个零点在区间(0,1)上,另一个零点在区间(1,2)上.
解 已知函数对应的方程为7x2-(a+13)x+a2-a-2=0,
函数的大致图象如图所示.
根据方程的根与函数的零点的关系,
方程的根一个在(0,1)上,另一个在(1,2)上,
∴-2<a<-1或3<a<4.
返回
解析答案
谢
谢
