沪教版(上海)高一数学上册 第1章 集合和命题 复习 课件(共29张PPT)
文档属性
| 名称 | 沪教版(上海)高一数学上册 第1章 集合和命题 复习 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-06 00:00:00 | ||
图片预览







文档简介
(共29张PPT)
第1章
集合和命题
复习课件
知识梳理
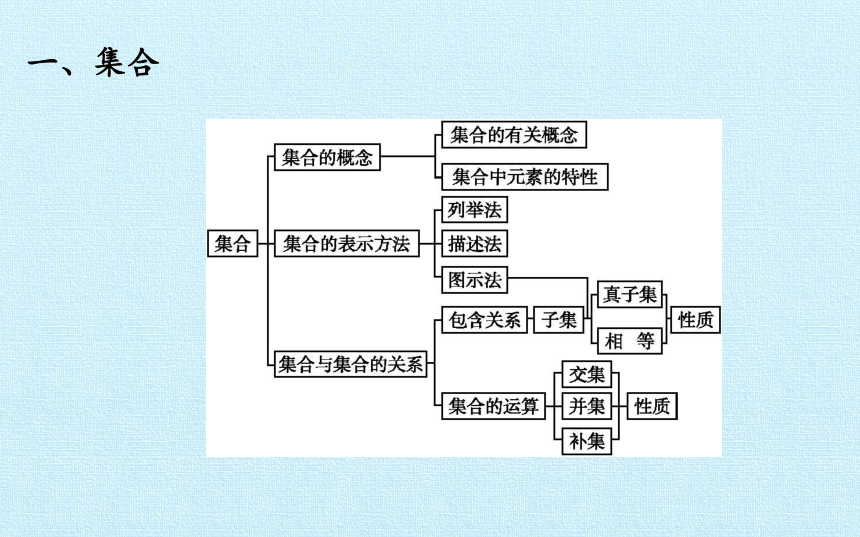
一、集合
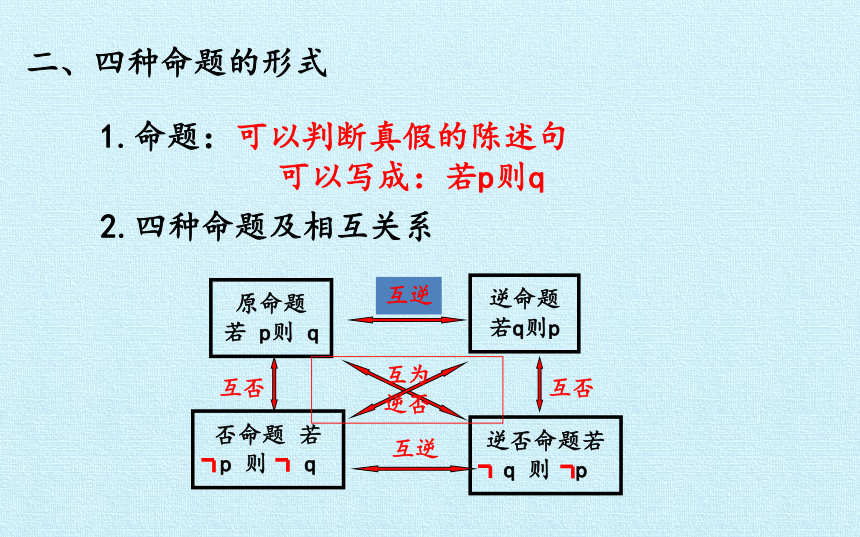
2.四种命题及相互关系
1.命题:可以判断真假的陈述句
可以写成:若p则q
原命题
若
p则
q
逆命题
若q则p
否命题
若
p
则
q
逆否命题若
q
则
p
互逆
互逆
互否
互否
互为
逆否
二、四种命题的形式
三、充分条件与必要条件
1.如果PQ,那么P是Q的充分条件,Q是P的必要条件;
2.如果PQ,那么P是Q的充要条件,也就是说,命题P与命题Q是等价命题。
应注意的问题
1.集合中的元素是确定的,各不相同的.
2.集合与元素的属于关系与集合之间的包含关系,两者不能混淆.
3.证明充分性的证明:.
4.原命题与它的逆否命题同真(假),因此它们是等价命题,逆命题与否命题互为逆否命题.
题型探究·素养提升
类型一
元素、集合与集合的关系
思路点拨:求解本题首先明确集合A和集合B的含义,再判断a与B的关系.
解:a∈A,因为a=n2+1=(n2+4n+4)-4(n+2)+5=(n+2)2-4(n+2)+5.
又因为n∈N+,所以n+2∈N+,所以a∈B.
【例1】
设集合A={a|a=n2+1,n∈N+},集合B={b|b=k2-4k+5,k∈N+},若已知a∈A,判断a与集合B的关系.
方法技巧
判断元素与集合的关系,首先要明确集合中元素的特征,其次要看元素是否满足集合中元素的公共属性,满足即为属于关系,不满足即为不属于关系.
思路点拨:先化简集合A,然后借助数轴,分类讨论.
方法技巧
利用不等式表示的集合的问题,常用数轴的直观图来解,特别要注意不等式边界值的取舍,含参数时要注意对集合空集的讨论.
类型二
集合的运算
【例3】
设A={-4,2a-1,a2},B={a-5,1-a,9},已知A∩B={9},求A∪B.
思路点拨:根据已知条件先求a,然后分别求出集合A,B,再利用并集的定义求A∪B.
解:因为A∩B={9},所以9∈A.
所以a2=9或2a-1=9,解得a=±3或a=5.
当a=3时,A={9,5,-4},B={-2,-2,9},B中元素不满足集合元素的互异性,舍去.
当a=-3时,A={9,-7,-4},B={-8,4,9},A∩B={9}满足题意,故A∪B={-7,
-4,-8,4,9}.
当a=5时,A={25,9,-4},B={0,-4,9},此时A∩B={-4,9},与A∩B={9}矛盾,故舍去.综上所述,A∪B={-7,-4,-8,4,9}.
方法技巧
求解含参数的集合交集、并集运算问题,求出参数的值后,应检验该参数的值是否满足集合中元素的性质.
方法技巧
利用不等式表示的集合的问题,常用数轴的直观图来解,特别要注意不等式边界值的取舍,含参数时要注意对集合空集的讨论.
类型三
补集思想
思路点拨:本题所给集合之间的关系是不等关系,求解时可以先从其对立面的相等关系求解,然后取其补集.
方法技巧
求解一些与不等式有关的集合问题时,若不易直接求解,或者较难分析,可利用“正难则反”的思想转化.“正难则反”策略运用的是补集思想,即已知全集U,求子集A,若直接求A困难,可先求?UA,再由?U(?UA)=A求A.
真
真
假
逆否命题
【例6】
判断下列命题的真假:
(1)已知
(2)若
(3)若
类型四
命题与充分条件、必要条件、充要条件的判断
【例7】
命题“若x2>1,则x<-1或x>1”的逆否命题是
A.若x2>1,则-1≤x≤1
B.若-1≤x≤1,则x2≤1
C.若-11
D.若x<-1或x>1,则x2>1
√
【例8】
集合A={|||≤4,},B={|},则“”是“”的( )
(A)充分不必要条件
(B)必要不充分条件
(C)充要条件
(D)既不充分也不必要条件
解析:
={|||≤4,},所以C.
方法技巧
命题真假与充分条件、必要条件的判断问题一般以选择题、填空题的形式进行考察,并且与其他数学知识考察融合在一起.因此,理解命题的四种形式,充分条件、必要条件、充要条件的含义是解题的基础,在此基础之上,再结合题目相关条件解决实际问题。
类型五
易错辨析
【例9】
设A={1,1+a,1+2a},B={1,b,b2},若A=B,求b的值.
【例10】
设A={x|2≤x≤6},B={x|2a≤x≤a+3},若B?A,则实数a的取值范围是( )
A.{a|1≤a≤3}
B.{a|a>3}
C.{a|a≥1}
D.{a|1纠错:空集是任何集合的子集,忽视这一点,会导致漏解,产生错误结论.
谢
谢
第1章
集合和命题
复习课件
知识梳理
一、集合
2.四种命题及相互关系
1.命题:可以判断真假的陈述句
可以写成:若p则q
原命题
若
p则
q
逆命题
若q则p
否命题
若
p
则
q
逆否命题若
q
则
p
互逆
互逆
互否
互否
互为
逆否
二、四种命题的形式
三、充分条件与必要条件
1.如果PQ,那么P是Q的充分条件,Q是P的必要条件;
2.如果PQ,那么P是Q的充要条件,也就是说,命题P与命题Q是等价命题。
应注意的问题
1.集合中的元素是确定的,各不相同的.
2.集合与元素的属于关系与集合之间的包含关系,两者不能混淆.
3.证明充分性的证明:.
4.原命题与它的逆否命题同真(假),因此它们是等价命题,逆命题与否命题互为逆否命题.
题型探究·素养提升
类型一
元素、集合与集合的关系
思路点拨:求解本题首先明确集合A和集合B的含义,再判断a与B的关系.
解:a∈A,因为a=n2+1=(n2+4n+4)-4(n+2)+5=(n+2)2-4(n+2)+5.
又因为n∈N+,所以n+2∈N+,所以a∈B.
【例1】
设集合A={a|a=n2+1,n∈N+},集合B={b|b=k2-4k+5,k∈N+},若已知a∈A,判断a与集合B的关系.
方法技巧
判断元素与集合的关系,首先要明确集合中元素的特征,其次要看元素是否满足集合中元素的公共属性,满足即为属于关系,不满足即为不属于关系.
思路点拨:先化简集合A,然后借助数轴,分类讨论.
方法技巧
利用不等式表示的集合的问题,常用数轴的直观图来解,特别要注意不等式边界值的取舍,含参数时要注意对集合空集的讨论.
类型二
集合的运算
【例3】
设A={-4,2a-1,a2},B={a-5,1-a,9},已知A∩B={9},求A∪B.
思路点拨:根据已知条件先求a,然后分别求出集合A,B,再利用并集的定义求A∪B.
解:因为A∩B={9},所以9∈A.
所以a2=9或2a-1=9,解得a=±3或a=5.
当a=3时,A={9,5,-4},B={-2,-2,9},B中元素不满足集合元素的互异性,舍去.
当a=-3时,A={9,-7,-4},B={-8,4,9},A∩B={9}满足题意,故A∪B={-7,
-4,-8,4,9}.
当a=5时,A={25,9,-4},B={0,-4,9},此时A∩B={-4,9},与A∩B={9}矛盾,故舍去.综上所述,A∪B={-7,-4,-8,4,9}.
方法技巧
求解含参数的集合交集、并集运算问题,求出参数的值后,应检验该参数的值是否满足集合中元素的性质.
方法技巧
利用不等式表示的集合的问题,常用数轴的直观图来解,特别要注意不等式边界值的取舍,含参数时要注意对集合空集的讨论.
类型三
补集思想
思路点拨:本题所给集合之间的关系是不等关系,求解时可以先从其对立面的相等关系求解,然后取其补集.
方法技巧
求解一些与不等式有关的集合问题时,若不易直接求解,或者较难分析,可利用“正难则反”的思想转化.“正难则反”策略运用的是补集思想,即已知全集U,求子集A,若直接求A困难,可先求?UA,再由?U(?UA)=A求A.
真
真
假
逆否命题
【例6】
判断下列命题的真假:
(1)已知
(2)若
(3)若
类型四
命题与充分条件、必要条件、充要条件的判断
【例7】
命题“若x2>1,则x<-1或x>1”的逆否命题是
A.若x2>1,则-1≤x≤1
B.若-1≤x≤1,则x2≤1
C.若-1
D.若x<-1或x>1,则x2>1
√
【例8】
集合A={|||≤4,},B={|},则“”是“”的( )
(A)充分不必要条件
(B)必要不充分条件
(C)充要条件
(D)既不充分也不必要条件
解析:
={|||≤4,},所以C.
方法技巧
命题真假与充分条件、必要条件的判断问题一般以选择题、填空题的形式进行考察,并且与其他数学知识考察融合在一起.因此,理解命题的四种形式,充分条件、必要条件、充要条件的含义是解题的基础,在此基础之上,再结合题目相关条件解决实际问题。
类型五
易错辨析
【例9】
设A={1,1+a,1+2a},B={1,b,b2},若A=B,求b的值.
【例10】
设A={x|2≤x≤6},B={x|2a≤x≤a+3},若B?A,则实数a的取值范围是( )
A.{a|1≤a≤3}
B.{a|a>3}
C.{a|a≥1}
D.{a|1
谢
谢
