沪教版(上海)高一数学上册 2.5 不等式的证明_1 课件(共22张PPT)
文档属性
| 名称 | 沪教版(上海)高一数学上册 2.5 不等式的证明_1 课件(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 680.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-06 00:00:00 | ||
图片预览








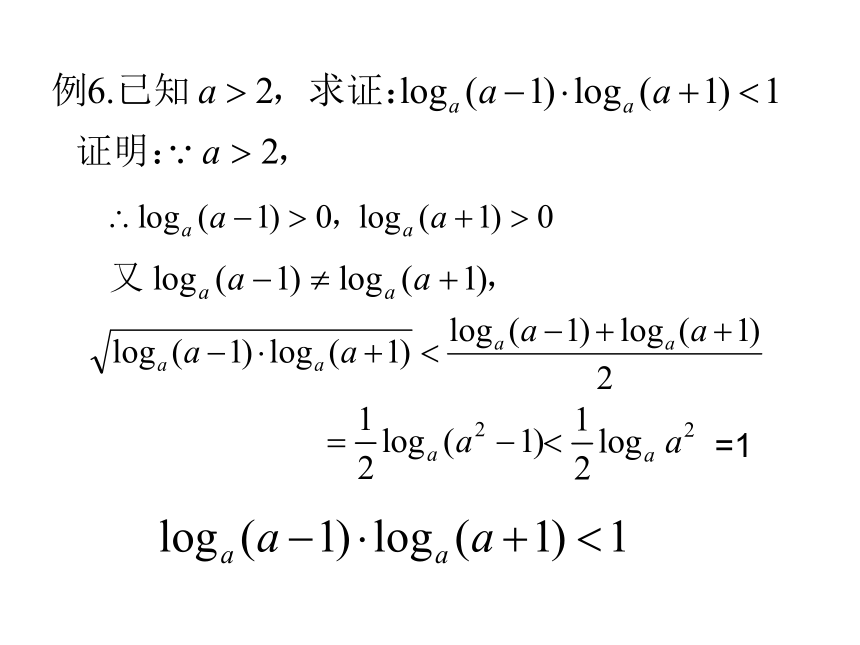
文档简介
(共22张PPT)
一、复习比较两个实数大小的主要方法:
(1)作差比较法:作差——变形——与0比较大小
(2)作商比较法:作商——变形——与1比较大小
例1.求证:
证:∵
≥
1.变形的目的全在于判断差的符号,而不必考虑差的值是
多少。至于怎样变形,要灵活处理。
2.本题的变形方法——配方法
二、比较法证明不等式:
例2.已知
都是正数,并且
求证
证明:
∵
都是正数,
并且
即:
1.本题变形的方法—通分法
2.本题的结论反映了分式的一个性质:若
都是正数,
当
时,
当
时,
例3.
已知
都是正数,并且
,
求证:
证明:
∵
都是正数,
∴
又∵
即:
本题变形的方法—
因式分解法
小结:
比较法是证明不等式的一种最基本、最重要的一种方法,用比较法证明不等式的步骤是:作差—变形—判断符号
要灵活掌握配方法和通分法对差式进行恒等变形。
利用已经证明过的不等式(如均值不等式及其变形式)和
不等式的性质推导出所要证明的不等式成立,这种证明方法
叫做综合法。
三、综合法证明不等式:
例4.已知
是不全相等的正数,求证:
证明:∵
三式中不能
全取“=”号,从而①②③式也不能全取“=”号,
由例5可得一个重要的不等式:
=1
小结:
综合法是证明不等式的基本方法,用综合法证明不等式
的逻辑关系是:
为证明过的
不等式,
要证的不等式)。
即综合法是:由因导果
从求证的不等式出发,分析寻找使这个不等式成立的
充分条件,把证明这个不等式的问题转化为判定这些条件
是否具备的问题。如果最后能够肯定这些条件都已具备,
那么就可以断定所求证的不等式成立。这种证明方法通常
叫做分析法。
四、分析法证明不等式:
例1.已知
都是正数,并且
求证
证明:
∵
都是正数,
本题的结论反映了分式的一个性质:若
都是正数,
当
时,
当
时,
为了要证明
只需证明
因此,只需证明
例2.
求证:.
所以为了证明
只需证明
展开得
证明某些含有根式的不等式时,用综合法比较困
难。例如,在例2中我们很难想到从”21<25“入手。
在不等式的证明中,分析法占有重要位置。我们常用
分析法探索证明的途径,然后用综合法的形式写出证
明过程。这是解决数学问题的一种重要思想。
分析法的思路是“执果索因”,即从求证的不等
式出发,不断地充分条件来代替前面的不等式,直
至找到已知的不等式为止。
例3.证明:当周长相等时,圆的面积比正方形的
面积大。
证明:设周长为
依题意,圆的面积为
正方形的面积为
所以本题只需证明
为了证明上式成立,只需证明
因此只需证明
上式是成立的,所以
这就证明了,如果周长相等,那么
圆的面积比正方形的面积大。
证明不等式的主要方法
一、比较法:
二、分析法:
三、综合法:
综合法证明不等式是“由因导果”
分析法证明不等式是“由果导因”
四、其它方法:
反证法
换元法
放缩法
课堂小结:
一、复习比较两个实数大小的主要方法:
(1)作差比较法:作差——变形——与0比较大小
(2)作商比较法:作商——变形——与1比较大小
例1.求证:
证:∵
≥
1.变形的目的全在于判断差的符号,而不必考虑差的值是
多少。至于怎样变形,要灵活处理。
2.本题的变形方法——配方法
二、比较法证明不等式:
例2.已知
都是正数,并且
求证
证明:
∵
都是正数,
并且
即:
1.本题变形的方法—通分法
2.本题的结论反映了分式的一个性质:若
都是正数,
当
时,
当
时,
例3.
已知
都是正数,并且
,
求证:
证明:
∵
都是正数,
∴
又∵
即:
本题变形的方法—
因式分解法
小结:
比较法是证明不等式的一种最基本、最重要的一种方法,用比较法证明不等式的步骤是:作差—变形—判断符号
要灵活掌握配方法和通分法对差式进行恒等变形。
利用已经证明过的不等式(如均值不等式及其变形式)和
不等式的性质推导出所要证明的不等式成立,这种证明方法
叫做综合法。
三、综合法证明不等式:
例4.已知
是不全相等的正数,求证:
证明:∵
三式中不能
全取“=”号,从而①②③式也不能全取“=”号,
由例5可得一个重要的不等式:
=1
小结:
综合法是证明不等式的基本方法,用综合法证明不等式
的逻辑关系是:
为证明过的
不等式,
要证的不等式)。
即综合法是:由因导果
从求证的不等式出发,分析寻找使这个不等式成立的
充分条件,把证明这个不等式的问题转化为判定这些条件
是否具备的问题。如果最后能够肯定这些条件都已具备,
那么就可以断定所求证的不等式成立。这种证明方法通常
叫做分析法。
四、分析法证明不等式:
例1.已知
都是正数,并且
求证
证明:
∵
都是正数,
本题的结论反映了分式的一个性质:若
都是正数,
当
时,
当
时,
为了要证明
只需证明
因此,只需证明
例2.
求证:.
所以为了证明
只需证明
展开得
证明某些含有根式的不等式时,用综合法比较困
难。例如,在例2中我们很难想到从”21<25“入手。
在不等式的证明中,分析法占有重要位置。我们常用
分析法探索证明的途径,然后用综合法的形式写出证
明过程。这是解决数学问题的一种重要思想。
分析法的思路是“执果索因”,即从求证的不等
式出发,不断地充分条件来代替前面的不等式,直
至找到已知的不等式为止。
例3.证明:当周长相等时,圆的面积比正方形的
面积大。
证明:设周长为
依题意,圆的面积为
正方形的面积为
所以本题只需证明
为了证明上式成立,只需证明
因此只需证明
上式是成立的,所以
这就证明了,如果周长相等,那么
圆的面积比正方形的面积大。
证明不等式的主要方法
一、比较法:
二、分析法:
三、综合法:
综合法证明不等式是“由因导果”
分析法证明不等式是“由果导因”
四、其它方法:
反证法
换元法
放缩法
课堂小结:
