沪教版(上海)高一数学上册 1.5 充分条件,必要条件_1 课件(共15张PPT)
文档属性
| 名称 | 沪教版(上海)高一数学上册 1.5 充分条件,必要条件_1 课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 724.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-06 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
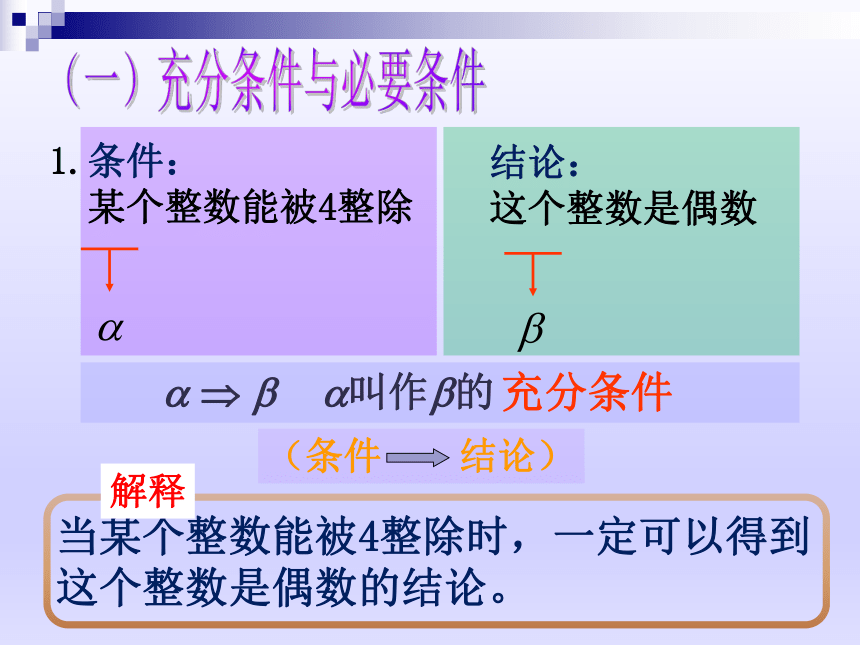
充分条件,必要条件
1.条件:
某个整数能被4整除
结论:
这个整数是偶数
充分条件
(条件
结论)
当某个整数能被4整除时,一定可以得到这个整数是偶数的结论。
解释
可以推出
吗?
“若某个整数能被4整除,则这个整数是偶数。”
2.条件:
某个整数是偶数
结论:
这个整数能被4整除
必要条件
(结论
条件)
不能
考察此命题的逆否命题
若这个整数不是偶数,则这个整数不能被4整除。
可见偶数是这个整数能被4整除必须要有的条件,不可或缺。
解释
总结
1、认清条件和结论
情况1:“……”是“……”的_____条件
条件
结论
情况2:“……”的_____条件是“……”
结论
条件
2、条件
结论
结论
条件
则条件是结论的充分条件
若反之不然,则条件是结论的充分非必要条件
则条件是结论的必要条件
若反之不然,则条件是结论的必要非充分条件
结论
条件
则条件是结论的充要条件
若都不成立,则条件是结论的既非充分又
非必要条件
例如:质数是奇数。
必要非充分
充分非必要
充分非必要
必要非充分
既非充分又非必要
举例
B
(2)已知A是B的充分非必要条件,B是C的充要条件,D是C的必要非充分条件,则D是A的(
)条件
必要非充分
举例
证明(1)充分性
充分性成立
(2)必要性
找好条件结论
条件到结论
结论到条件
(舍)
(舍)
必要性成立
综上:
证明(1)充分性
充分性成立
(2)必要性
条件到结论
举反例
必要性不成立
解:是必要非充分条件,下面证明
必要性成立
充分性不成立
说明:
(1)肯定充分性和必要性要通过直接证明,否定则需要举反例即可;
(2)充分必要条件的证明需两方面都要考虑(除非题目只要求证一方面).
的_________________条件
的_________________条件
举例
小结
1.
2.条件与结论之间的关系分为:
充分非必要条件、必要非充分条件
充要条件、既非充分又非必要条件
3.充要条件的证明需两方面都要考虑,即充分性、必要性。
作业:课后练习
充分条件,必要条件
1.条件:
某个整数能被4整除
结论:
这个整数是偶数
充分条件
(条件
结论)
当某个整数能被4整除时,一定可以得到这个整数是偶数的结论。
解释
可以推出
吗?
“若某个整数能被4整除,则这个整数是偶数。”
2.条件:
某个整数是偶数
结论:
这个整数能被4整除
必要条件
(结论
条件)
不能
考察此命题的逆否命题
若这个整数不是偶数,则这个整数不能被4整除。
可见偶数是这个整数能被4整除必须要有的条件,不可或缺。
解释
总结
1、认清条件和结论
情况1:“……”是“……”的_____条件
条件
结论
情况2:“……”的_____条件是“……”
结论
条件
2、条件
结论
结论
条件
则条件是结论的充分条件
若反之不然,则条件是结论的充分非必要条件
则条件是结论的必要条件
若反之不然,则条件是结论的必要非充分条件
结论
条件
则条件是结论的充要条件
若都不成立,则条件是结论的既非充分又
非必要条件
例如:质数是奇数。
必要非充分
充分非必要
充分非必要
必要非充分
既非充分又非必要
举例
B
(2)已知A是B的充分非必要条件,B是C的充要条件,D是C的必要非充分条件,则D是A的(
)条件
必要非充分
举例
证明(1)充分性
充分性成立
(2)必要性
找好条件结论
条件到结论
结论到条件
(舍)
(舍)
必要性成立
综上:
证明(1)充分性
充分性成立
(2)必要性
条件到结论
举反例
必要性不成立
解:是必要非充分条件,下面证明
必要性成立
充分性不成立
说明:
(1)肯定充分性和必要性要通过直接证明,否定则需要举反例即可;
(2)充分必要条件的证明需两方面都要考虑(除非题目只要求证一方面).
的_________________条件
的_________________条件
举例
小结
1.
2.条件与结论之间的关系分为:
充分非必要条件、必要非充分条件
充要条件、既非充分又非必要条件
3.充要条件的证明需两方面都要考虑,即充分性、必要性。
作业:课后练习
