人教版八年级上册第十一章11.1-11.2 与三角形有关的线段和角 同步测试卷(word解析版)
文档属性
| 名称 | 人教版八年级上册第十一章11.1-11.2 与三角形有关的线段和角 同步测试卷(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 404.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-04 20:38:09 | ||
图片预览



文档简介
《与三角形有关的线段和角》单元测试卷
考试范围:新人教版八年级上册11.1~11.2;考试时间:100分钟;满分:120分
学校:___________姓名:___________班级:___________考号:___________
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)下列各图中,正确画出AC边上的高的是( )
A.
B.
C.
D.
2.(3分)下列长度的三根小木棒能构成三角形的是( )
A.2cm,3cm,5cm
B.7cm,4cm,2cm
C.3cm,4cm,8cm
D.3cm,3cm,4cm
3.(3分)下列图形中有稳定性的是( )
A.正方形
B.长方形
C.直角三角形
D.平行四边形
4.(3分)在△ABC中,若∠A=95°,∠B=40°,则∠C的度数为( )
A.35°
B.40°
C.45°
D.50°
5.(3分)如图,AE是△ABC的中线,已知EC=6,DE=2,则BD的长为( )
A.2
B.3
C.4
D.6
6.(3分)如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=( )
A.35°
B.95°
C.85°
D.75°
7.(3分)如图,CD,CE,CF分别是△ABC的高、角平分线、中线,则下列各式中错误的是( )
A.AB=2BF
B.∠ACE=∠ACB
C.AE=BE
D.CD⊥BE
8.(3分)如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC=( )
A.118°
B.119°
C.120°
D.121°
9.(3分)若一个三角形的三条边长分别为3,2a﹣1,6,则整数a的值可能是( )
A.2,3
B.3,4
C.2,3,4
D.3,4,5
10.(3分)如图,已知AF平分∠BAC,过F作FD⊥BC,若∠B比∠C
大20度,则∠F的度数是( )
A.10度
B.15度
C.20度
D.不能确定
二.填空题(共8小题,满分24分,每小题3分)
11.(3分)如图,△ABC中,AD⊥BC于D,点E在CD上,则图中
以AD为高的三角形有
个.
12.(3分)如图,生活中都把自行车的几根梁做成三角形的支架,这是因为三角形具
有
性.
13.(3分)已知等腰三角形的两边长分别为4cm和8cm,则此三角形的周长为
cm.
14.(3分)将一副三角尺按如图所示的方式放置,使含30°角的三角尺的短直角边和含45°角的三角尺的一条直角边重合,则∠1的度数是
.
15.(3分)已知a、b、c为△ABC的三边,化简:|a+b﹣c|+|a﹣b﹣c|﹣|a﹣b+c|=
.
16.(3分)如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=30°,∠2=20°,则∠B=
.
17.(3分)当三角形中一个内角α是另一个内角β的一半时,我们称此三角形为“半角三角形”,其中α称为“半角”.如果一个“半角三角形”的“半角”为20°,那么这个“半角三角形”的最大内角的度数为
.
18.(3分)如图,△ABC三边的中线AD、BE、CF的公共点为G,若S△ABC=12,则图中阴影部分的面积是
.
三.解答题(共7小题,满分66分)
19.(9分)已知△ABC(如图).
(1)画BC上的高;
(2)画∠B的平分线;
(3)画AB上的中线.
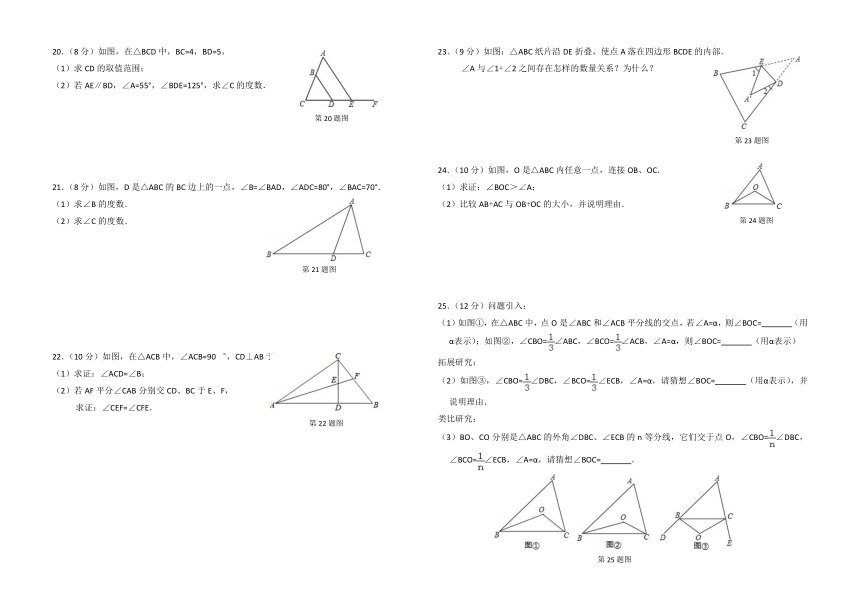
20.(8分)如图,在△BCD中,BC=4,BD=5,
(1)求CD的取值范围;
(2)若AE∥BD,∠A=55°,∠BDE=125°,求∠C的度数.
21.(8分)如图,D是△ABC的BC边上的一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°.
(1)求∠B的度数.
(2)求∠C的度数.
22.(10分)如图,在△ACB中,∠ACB=90゜,CD⊥AB于D.
(1)求证:∠ACD=∠B;
(2)若AF平分∠CAB分别交CD、BC于E、F,
求证:∠CEF=∠CFE.
23.(9分)如图:△ABC纸片沿DE折叠,使点A落在四边形BCDE的内部.
∠A与∠1+∠2之间存在怎样的数量关系?为什么?
24.(10分)如图,O是△ABC内任意一点,连接OB、OC.
(1)求证:∠BOC>∠A;
(2)比较AB+AC与OB+OC的大小,并说明理由.
25.(12分)问题引入:
(1)如图①,在△ABC中,点O是∠ABC和∠ACB平分线的交点,若∠A=α,则∠BOC=
(用α表示);如图②,∠CBO=∠ABC,∠BCO=∠ACB,∠A=α,则∠BOC=
(用α表示)
拓展研究:
(2)如图③,∠CBO=∠DBC,∠BCO=∠ECB,∠A=α,请猜想∠BOC=
(用α表示),并说明理由.
类比研究:
(3)BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线,它们交于点O,∠CBO=∠DBC,∠BCO=∠ECB,∠A=α,请猜想∠BOC=
.
《与三角形有关的线段和角》单元测试卷
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
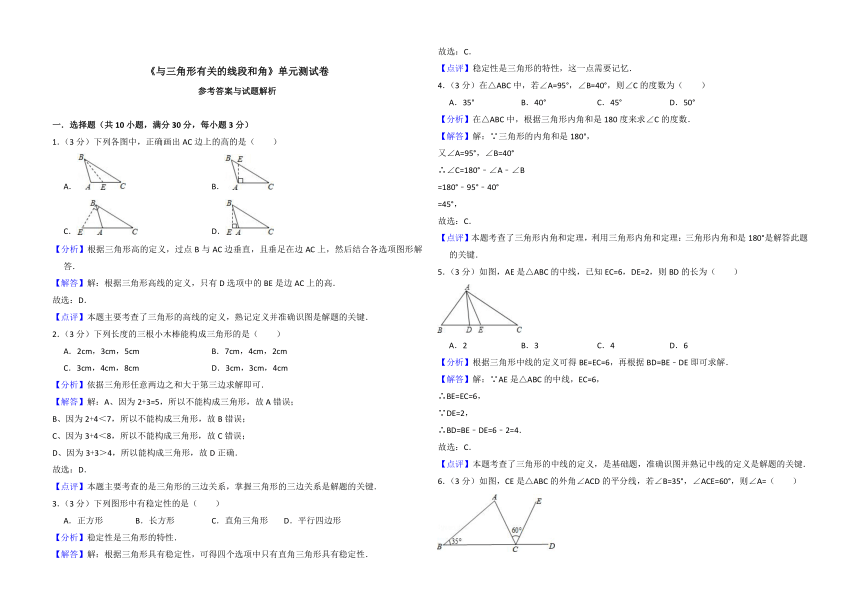
1.(3分)下列各图中,正确画出AC边上的高的是( )
A.
B.
C.
D.
【分析】根据三角形高的定义,过点B与AC边垂直,且垂足在边AC上,然后结合各选项图形解答.
【解答】解:根据三角形高线的定义,只有D选项中的BE是边AC上的高.
故选:D.
【点评】本题主要考查了三角形的高线的定义,熟记定义并准确识图是解题的关键.
2.(3分)下列长度的三根小木棒能构成三角形的是( )
A.2cm,3cm,5cm
B.7cm,4cm,2cm
C.3cm,4cm,8cm
D.3cm,3cm,4cm
【分析】依据三角形任意两边之和大于第三边求解即可.
【解答】解:A、因为2+3=5,所以不能构成三角形,故A错误;
B、因为2+4<7,所以不能构成三角形,故B错误;
C、因为3+4<8,所以不能构成三角形,故C错误;
D、因为3+3>4,所以能构成三角形,故D正确.
故选:D.
【点评】本题主要考查的是三角形的三边关系,掌握三角形的三边关系是解题的关键.
3.(3分)下列图形中有稳定性的是( )
A.正方形
B.长方形
C.直角三角形
D.平行四边形
【分析】稳定性是三角形的特性.
【解答】解:根据三角形具有稳定性,可得四个选项中只有直角三角形具有稳定性.
故选:C.
【点评】稳定性是三角形的特性,这一点需要记忆.
4.(3分)在△ABC中,若∠A=95°,∠B=40°,则∠C的度数为( )
A.35°
B.40°
C.45°
D.50°
【分析】在△ABC中,根据三角形内角和是180度来求∠C的度数.
【解答】解:∵三角形的内角和是180°,
又∠A=95°,∠B=40°
∴∠C=180°﹣∠A﹣∠B
=180°﹣95°﹣40°
=45°,
故选:C.
【点评】本题考查了三角形内角和定理,利用三角形内角和定理:三角形内角和是180°是解答此题的关键.
5.(3分)如图,AE是△ABC的中线,已知EC=6,DE=2,则BD的长为( )
A.2
B.3
C.4
D.6
【分析】根据三角形中线的定义可得BE=EC=6,再根据BD=BE﹣DE即可求解.
【解答】解:∵AE是△ABC的中线,EC=6,
∴BE=EC=6,
∵DE=2,
∴BD=BE﹣DE=6﹣2=4.
故选:C.
【点评】本题考查了三角形的中线的定义,是基础题,准确识图并熟记中线的定义是解题的关键.
6.(3分)如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=( )
A.35°
B.95°
C.85°
D.75°
【分析】根据三角形角平分线的性质求出∠ACD,根据三角形外角性质求出∠A即可.
【解答】解:∵CE是△ABC的外角∠ACD的平分线,∠ACE=60°,
∴∠ACD=2∠ACE=120°,
∵∠ACD=∠B+∠A,
∴∠A=∠ACD﹣∠B=120°﹣35°=85°,
故选:C.
【点评】本题考查了三角形外角性质,角平分线定义的应用,注意:三角形的一个外角等于和它不相邻的两个内角的和.
7.(3分)如图,CD,CE,CF分别是△ABC的高、角平分线、中线,则下列各式中错误的是( )
A.AB=2BF
B.∠ACE=∠ACB
C.AE=BE
D.CD⊥BE
【分析】从三角形的一个顶点向对边作垂线,垂足与顶点之间的线段叫做三角形的高.
三角形一个内角的平分线与这个内角的对边交于一点,则这个内角的顶点与所交的点间的线段叫做三角形的角平分线.
三角形一边的中点与此边所对顶点的连线叫做三角形的中线.依此即可求解.
【解答】解:∵CD,CE,CF分别是△ABC的高、角平分线、中线,
∴CD⊥BE,∠ACE=∠ACB,AB=2BF,无法确定AE=BE.
故选:C.
【点评】考查了三角形的角平分线、中线和高,根据是熟悉它们的定义和性质.
8.(3分)如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC=( )
A.118°
B.119°
C.120°
D.121°
【分析】由三角形内角和定理得∠ABC+∠ACB=120°,由角平分线的性质得∠CBE+∠BCD=60°,再利用三角形的内角和定理得结果.
【解答】解:∵∠A=60°,
∴∠ABC+∠ACB=120°,
∵BE,CD是∠B、∠C的平分线,
∴∠CBE=∠ABC,∠BCD=,
∴∠CBE+∠BCD=(∠ABC+∠BCA)=60°,
∴∠BFC=180°﹣60°=120°,
故选:C.
【点评】本题主要考查了三角形内角和定理和角平分线的性质,综合运用三角形内角和定理和角平分线的性质是解答此题的关键.
9.(3分)若一个三角形的三条边长分别为3,2a﹣1,6,则整数a的值可能是( )
A.2,3
B.3,4
C.2,3,4
D.3,4,5
【分析】直接利用三角形三边关系得出a的取值范围,进而得出答案.
【解答】解:∵一个三角形的三条边长分别为3,2a﹣1,6,
∴,
解得:2<a<5,
故整数a的值可能是:3,4.
故选:B.
【点评】此题主要考查了三角形三边关系,正确得出a的取值范围是解题关键.
10.(3分)如图,已知AF平分∠BAC,过F作FD⊥BC,若∠B比∠C大20度,则∠F的度数是( )
A.10度
B.15度
C.20度
D.不能确定
【分析】根据题意可知∠B=20°+∠C,根据三角形的内角和定理可知∠ADC+∠DAC+∠C=180°,∠ADC=∠B+∠BAF,根据角平分线的性质,可知∠EAC=∠BAF,可得出∠ADC=100°,再根据FD⊥BC,可得出∠F的度数.
【解答】解:∵∠B比∠C大20度,
∴∠B=20°+∠C,
∵AF平分∠BAC,
∴∠EAC=∠BAF,
∵∠ADC+∠BAF+∠B﹣20°=180°,
∠ADC=∠B+∠BAF,
得出∠BAF+∠B=100°,
∴∠ADC=100°,
∵FD⊥BC,
∴∠ADC=90°+∠F=100°,
∴∠F=10°.
故选:A.
【点评】本题主要考查了三角形的内角和定理,角平分线的性质,以及三角形的外角等于与它不相邻的两内角和,比较综合,难度适中.
二.填空题(共8小题,满分24分,每小题3分)
11.(3分)如图,△ABC中,AD⊥BC于D,点E在CD上,则图中以AD为高的三角形有 6 个.
【分析】由于AD⊥BC于D,图中共有6个三角形,它们都有一边在直线CB上,由此即可确定以AD为高的三角形的个数.
【解答】解:∵AD⊥BC于D,
而图中有一边在直线CB上,且以A为顶点的三角形有6个,
∴以AD为高的三角形有6个.
故答案为:6.
【点评】此题主要考查了三角形的高,三角形的高可以在三角形外,可以是三角形的边,也可以在三角形内,所以确定三角形的高比较灵活.
12.(3分)如图,生活中都把自行车的几根梁做成三角形的支架,这是因为三角形具有 稳定 性.
【分析】根据三角形具有稳定性解答.
【解答】解:生活中都把自行车的几根梁做成三角形的支架,这是因为三角形具有稳定性.
故答案为:稳定.
【点评】本题考查三角形稳定性的实际应用.三角形的稳定性在实际生活中有着广泛的应用,如钢架桥、房屋架梁等,因此要使一些图形具有稳定的结构,往往通过连接辅助线转化为三角形而获得.
13.(3分)已知等腰三角形的两边长分别为4cm和8cm,则此三角形的周长为 20 cm.
【分析】根据等腰三角形的性质,本题要分情况讨论.当腰长为4cm或是腰长为8cm两种情况.
【解答】解:等腰三角形的两边长分别为4cm和8cm,
当腰长是4cm时,则三角形的三边是4cm,4cm,8cm,4cm+4cm=8cm不满足三角形的三边关系;
当腰长是8cm时,三角形的三边是8cm,8cm,4cm,三角形的周长是20cm.
故填20.
【点评】本题考查了等腰三角形的性质和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,进行分类讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.
14.(3分)将一副三角尺按如图所示的方式放置,使含30°角的三角尺的短直角边和含45°角的三角尺的一条直角边重合,则∠1的度数是 75° .
【分析】根据含30°角的三角尺的短直角边和含45°角的三角尺的一条直角边重合,得出平行线,再利用平行线的性质和对顶角相等得出∠2=45°,再利用三角形的外角性质解答即可.
【解答】解:如图,
∵含30°角的三角尺的短直角边和含45°角的三角尺的一条直角边重合,
∴AB∥CD,
∴∠3=∠4=45°,
∴∠2=∠3=45°,
∵∠B=30°,
∴∠1=∠2+∠B=30°+45°=75°,
故答案为:75°.
【点评】此题考查三角形外角性质,关键是利用平行线性质和对顶角相等得出∠2的度数.
15.(3分)已知a、b、c为△ABC的三边,化简:|a+b﹣c|+|a﹣b﹣c|﹣|a﹣b+c|= ﹣a+3b﹣c .
【分析】根据三角形三边关系:两边之和大于第三边,两边之差小于第三边,来判定绝对值里的式子的正负值,然后去绝对值进行计算即可.
【解答】解:|a+b﹣c|+|a﹣b﹣c|﹣|a﹣b+c|,
=(a+b﹣c)+(﹣a+b+c)﹣(a﹣b+c),
=a+b﹣c﹣a+b+c﹣a+b﹣c,
=﹣a+3b﹣c,
故答案为:﹣a+3b﹣c.
【点评】此题主要考查了三角形三边关系,以及绝对值的性质,关键是掌握三边关系定理.
16.(3分)如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=30°,∠2=20°,则∠B= 50° .
【分析】由AE平分∠BAC,可得角相等,由∠1=30°,∠2=20°,可求得∠EAD的度数,在直角三角形ABD在利用两锐角互余可求得答案.
【解答】解:∵AE平分∠BAC,
∴∠1=∠EAD+∠2,
∴∠EAD=∠1﹣∠2=30°﹣20°=10°,
Rt△ABD中,∠B=90°﹣∠BAD
=90°﹣30°﹣10°=50°.
故答案为50°.
【点评】本题考查了三角形的角平分线、中线和高的相关知识;求得∠EAD=10°是正确解答本题的关键.
17.(3分)当三角形中一个内角α是另一个内角β的一半时,我们称此三角形为“半角三角形”,其中α称为“半角”.如果一个“半角三角形”的“半角”为20°,那么这个“半角三角形”的最大内角的度数为 120° .
【分析】根据半角三角形的定义得出β的度数,再由三角形内角和定理求出另一个内角即可.
【解答】解:∵α=20°,
∴β=2α=40°,
∴最大内角的度数=180°﹣20°﹣40°=120°.
故答案为:120°.
【点评】本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.
18.(3分)如图,△ABC三边的中线AD、BE、CF的公共点为G,若S△ABC=12,则图中阴影部分的面积是 4 .
【分析】根据三角形的中线把三角形的面积分成相等的两部分,知△ABC的面积即为阴影部分的面积的3倍.
【解答】方法1
解:∵△ABC的三条中线AD、BE,CF交于点G,
∴S△CGE=S△AGE=S△ACF,S△BGF=S△BGD=S△BCF,
∵S△ACF=S△BCF=S△ABC=×12=6,
∴S△CGE=S△ACF=×6=2,S△BGF=S△BCF=×6=2,
∴S阴影=S△CGE+S△BGF=4.
故答案为4.
方法2
设△AFG,△BFG,△BDG,△CDG,△CEG,△AEG的面积分别为S1,S2,S3,S4,S5,S6,根据中线平分三角形面积可得:S1=S2,S3=S4,S5=S6,S1+S2+S3=S4+S5+S6①,S2+S3+S4=S1+S5+S6②
由①﹣②可得S1=S4,所以S1=S2=S3=S4=S5=S6=2,故阴影部分的面积为4.
故答案为:4.
【点评】根据三角形的中线把三角形的面积分成相等的两部分,该图中,△BGF的面积=△BGD的面积=△CGD的面积,△AGF的面积=△AGE的面积=△CGE的面积.
三.解答题(共7小题,满分66分)
19.(9分)已知△ABC(如图).
(1)画BC上的高;
(2)画∠B的平分线;
(3)画AB上的中线.
【分析】(1)过A作BC的垂线交CB的延长线于点D,则AD就是BC上的高;
(2)作∠ABC的平分线交AC于点E,则BE就是∠B的平分线;
(3)先作AB的垂直平分线,得到AB的中点是F,连接CF,则CF就是AB上的中线.
【解答】解:(1)①以点A为圆心,以适当长度(只要与CB的延长线有两个交点即可)为半径,画弧交CB的延长线于两点,
②以两个交点为圆心,以大于两点之间距离的一半为半径画弧,两弧交于一点,
③过点A与交点作直线与CB的延长线相交于点D,
则AD就是所要求作的BC上的高;
(2)①以点B为圆心,以任意长为半径画弧,分别于BA、BC边相交,
②分别以两交点为圆心,以大于两交点之间的距离的一半为半径画弧,两弧相交于一点,
连接点B与交点,交AC于点E,
则BE就是所要求作的∠B的平分线;
(3)①分别以点A、B为圆心,以大于AB为半径画弧,两弧相交于两点,
②连接这两个交点,交AB于点F,
③连接CF,
则CF就是所要求作的AB上的中线.
【点评】本题考查了过直线外一点作已知直线的作法,角平分线的作法,线段垂直平分线的作法,都是基本作图,需要熟练掌握.
20.(8分)如图,在△BCD中,BC=4,BD=5,
(1)求CD的取值范围;
(2)若AE∥BD,∠A=55°,∠BDE=125°,求∠C的度数.
【分析】(1)利用三角形三边关系得出DC的取值范围即可;
(2)利用平行线的性质得出∠AEC的度数,再利用三角形内角和定理得出答案.
【解答】解:(1)∵在△BCD中,BC=4,BD=5,
∴1<DC<9;
(2)∵AE∥BD,∠BDE=125°,
∴∠AEC=55°,
又∵∠A=55°,
∴∠C=70°.
【点评】此题主要考查了三角形三边关系以及平行线的性质,得出∠AEC的度数是解题关键.
21.(8分)如图,D是△ABC的BC边上的一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°.
(1)求∠B的度数.
(2)求∠C的度数.
【分析】(1)先由三角形外角的性质得出∠ADC=∠B+∠BAD,再由∠ADC=80°,∠B=∠BAD即可得出∠B的度数;
(2)直接根据三角形的内角和定理得出∠C的度数.
【解答】解:(1)∵∠ADC是△ABD的一个外角,
∴∠ADC=∠B+∠BAD,
又∵∠ADC=80°,∠B=∠BAD,
∴∠B=∠ADC=×80°=40°;
(2)在△ABC
中,
∵∠BAC+∠B+∠C=180°,
∴∠C=180°﹣∠B﹣∠BAC=180°﹣40°﹣70°=70°.
【点评】本题考查的是三角形内角和定理及外角的性质,熟知三角形的内角和是180°是解答此题的关键.
22.(10分)如图,在△ACB中,∠ACB=90゜,CD⊥AB于D.
(1)求证:∠ACD=∠B;
(2)若AF平分∠CAB分别交CD、BC于E、F,求证:∠CEF=∠CFE.
【分析】(1)由于∠ACD与∠B都是∠BCD的余角,根据同角的余角相等即可得证;
(2)根据直角三角形两锐角互余得出∠CFA=90°﹣∠CAF,∠AED=90°﹣∠DAE,再根据角平分线的定义得出∠CAF=∠DAE,然后由对顶角相等的性质,等量代换即可证明∠CEF=∠CFE.
【解答】证明:(1)∵∠ACB=90゜,CD⊥AB于D,
∴∠ACD+∠BCD=90°,∠B+∠BCD=90°,
∴∠ACD=∠B;
(2)在Rt△AFC中,∠CFA=90°﹣∠CAF,
同理在Rt△AED中,∠AED=90°﹣∠DAE.
又∵AF平分∠CAB,
∴∠CAF=∠DAE,
∴∠AED=∠CFE,
又∵∠CEF=∠AED,
∴∠CEF=∠CFE.
【点评】本题考查了直角三角形的性质,三角形角平分线的定义,对顶角的性质,余角的性质,难度适中.
23.(9分)如图:△ABC纸片沿DE折叠,使点A落在四边形BCDE的内部.∠A与∠1+∠2之间存在怎样的数量关系?为什么?
【分析】本题可根据四边形的内角和为360°及翻折的性质,就可求出2∠A=∠1+∠2这一始终保持不变的性质.
【解答】解:2∠A=∠1+∠2,
理由:∵在四边形ADA′E中,∠A+∠A′+∠ADA′+∠AEA′=360°,
则2∠A+180°﹣∠2+180°﹣∠1=360°,
∴可得2∠A=∠1+∠2.
【点评】本题主要考查四边形的内角和及翻折的性质特点,解决本题的关键是熟记翻折的性质.
24.(10分)如图,O是△ABC内任意一点,连接OB、OC.
(1)求证:∠BOC>∠A;
(2)比较AB+AC与OB+OC的大小,并说明理由.
【分析】(1)延长BO交AC于点D,首先利用三角形的外角性质得到∠BOC>∠ODC,让根据∠ODC>∠A,证得∠BOC>∠A;
(2)根据三角形的三边关系证得AB+AD>OB+OD,OD+CD>OC,从而得到AB+AD+CD>OB+OC,进而得到AB+AC>OB+OC.
【解答】解:(1)证明:延长BO交AC于点D,
∴∠BOC>∠ODC,
又∠ODC>∠A,
∴∠BOC>∠A;
(2)AB+AC>OB+OC,
∵AB+AD>OB+OD,OD+CD>OC,
∴AB+AD+CD>OB+OC,
即:AB+AC>OB+OC.
【点评】本题考出了三角形的三边关系及三角形的外角的性质,解题的关键是能够正确的构造三角形,难度不大.
25.(12分)问题引入:
(1)如图①,在△ABC中,点O是∠ABC和∠ACB平分线的交点,若∠A=α,则∠BOC= 90°+α (用α表示);如图②,∠CBO=∠ABC,∠BCO=∠ACB,∠A=α,则∠BOC= 120°+α (用α表示)
拓展研究:
(2)如图③,∠CBO=∠DBC,∠BCO=∠ECB,∠A=α,请猜想∠BOC= 120°﹣α (用α表示),并说明理由.
类比研究:
(3)BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线,它们交于点O,∠CBO=∠DBC,∠BCO=∠ECB,∠A=α,请猜想∠BOC= ﹣α .
【分析】(1)如图①,根据角平分线的定义可得∠OBC=∠ABC,∠OCB=∠ACB,然后表示出∠OBC+∠OCB,再根据三角形的内角和等于180°列式整理即可得∠BOC=90°+α;如图②,根据三角形的内角和等于180°列式整理即可得∠BOC=120°+α;
(2)如图③,根据三角形的内角和等于180°列式整理即可得∠BOC=120°﹣α;
(3)根据三角形的内角和等于180°列式整理即可得∠BOC=﹣α.
【解答】解:(1)如图①,∵∠ABC与∠ACB的平分线相交于点O,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∴∠OBC+∠OCB=(∠ABC+∠ACB),
在△OBC中,∠BOC=180°﹣(∠OBC+∠OCB)
=180°﹣(∠ABC+∠ACB)
=180°﹣(180°﹣∠A)
=90°+∠A
=90°+α;
如图②,在△OBC中,∠BOC=180°﹣(∠OBC+∠OCB)
=180°﹣(∠ABC+∠ACB)
=180°﹣(180°﹣∠A)
=120°+∠A
=120°+α;
(2)如图③,在△OBC中,∠BOC=180°﹣(∠OBC+∠OCB)
=180°﹣(∠DBC+∠ECB)
=180°﹣(∠A+∠ACB+∠A+ABC)
=180°﹣(∠A+180°)
=120°﹣α;
(3)在△OBC中,∠BOC=180°﹣(∠OBC+∠OCB)
=180°﹣(∠DBC+∠ECB)
=180°﹣(∠A+∠ACB+∠A+ABC)
=180°﹣(∠A+180°)
=﹣α.
故答案为90°+α,120°+α;120°﹣α;﹣α.
【点评】本题考查了三角形的内角和定理,角平分线的定义,整体思想的利用是解题的关键.
第11题图
第12题图
第14题图
第16题图
第5题图
第6题图
第7题图
第8题图
第10题图
第18题图
第19题图
第20题图
第21题图
第22题图
第23题图
第24题图
第25题图
考试范围:新人教版八年级上册11.1~11.2;考试时间:100分钟;满分:120分
学校:___________姓名:___________班级:___________考号:___________
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)下列各图中,正确画出AC边上的高的是( )
A.
B.
C.
D.
2.(3分)下列长度的三根小木棒能构成三角形的是( )
A.2cm,3cm,5cm
B.7cm,4cm,2cm
C.3cm,4cm,8cm
D.3cm,3cm,4cm
3.(3分)下列图形中有稳定性的是( )
A.正方形
B.长方形
C.直角三角形
D.平行四边形
4.(3分)在△ABC中,若∠A=95°,∠B=40°,则∠C的度数为( )
A.35°
B.40°
C.45°
D.50°
5.(3分)如图,AE是△ABC的中线,已知EC=6,DE=2,则BD的长为( )
A.2
B.3
C.4
D.6
6.(3分)如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=( )
A.35°
B.95°
C.85°
D.75°
7.(3分)如图,CD,CE,CF分别是△ABC的高、角平分线、中线,则下列各式中错误的是( )
A.AB=2BF
B.∠ACE=∠ACB
C.AE=BE
D.CD⊥BE
8.(3分)如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC=( )
A.118°
B.119°
C.120°
D.121°
9.(3分)若一个三角形的三条边长分别为3,2a﹣1,6,则整数a的值可能是( )
A.2,3
B.3,4
C.2,3,4
D.3,4,5
10.(3分)如图,已知AF平分∠BAC,过F作FD⊥BC,若∠B比∠C
大20度,则∠F的度数是( )
A.10度
B.15度
C.20度
D.不能确定
二.填空题(共8小题,满分24分,每小题3分)
11.(3分)如图,△ABC中,AD⊥BC于D,点E在CD上,则图中
以AD为高的三角形有
个.
12.(3分)如图,生活中都把自行车的几根梁做成三角形的支架,这是因为三角形具
有
性.
13.(3分)已知等腰三角形的两边长分别为4cm和8cm,则此三角形的周长为
cm.
14.(3分)将一副三角尺按如图所示的方式放置,使含30°角的三角尺的短直角边和含45°角的三角尺的一条直角边重合,则∠1的度数是
.
15.(3分)已知a、b、c为△ABC的三边,化简:|a+b﹣c|+|a﹣b﹣c|﹣|a﹣b+c|=
.
16.(3分)如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=30°,∠2=20°,则∠B=
.
17.(3分)当三角形中一个内角α是另一个内角β的一半时,我们称此三角形为“半角三角形”,其中α称为“半角”.如果一个“半角三角形”的“半角”为20°,那么这个“半角三角形”的最大内角的度数为
.
18.(3分)如图,△ABC三边的中线AD、BE、CF的公共点为G,若S△ABC=12,则图中阴影部分的面积是
.
三.解答题(共7小题,满分66分)
19.(9分)已知△ABC(如图).
(1)画BC上的高;
(2)画∠B的平分线;
(3)画AB上的中线.
20.(8分)如图,在△BCD中,BC=4,BD=5,
(1)求CD的取值范围;
(2)若AE∥BD,∠A=55°,∠BDE=125°,求∠C的度数.
21.(8分)如图,D是△ABC的BC边上的一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°.
(1)求∠B的度数.
(2)求∠C的度数.
22.(10分)如图,在△ACB中,∠ACB=90゜,CD⊥AB于D.
(1)求证:∠ACD=∠B;
(2)若AF平分∠CAB分别交CD、BC于E、F,
求证:∠CEF=∠CFE.
23.(9分)如图:△ABC纸片沿DE折叠,使点A落在四边形BCDE的内部.
∠A与∠1+∠2之间存在怎样的数量关系?为什么?
24.(10分)如图,O是△ABC内任意一点,连接OB、OC.
(1)求证:∠BOC>∠A;
(2)比较AB+AC与OB+OC的大小,并说明理由.
25.(12分)问题引入:
(1)如图①,在△ABC中,点O是∠ABC和∠ACB平分线的交点,若∠A=α,则∠BOC=
(用α表示);如图②,∠CBO=∠ABC,∠BCO=∠ACB,∠A=α,则∠BOC=
(用α表示)
拓展研究:
(2)如图③,∠CBO=∠DBC,∠BCO=∠ECB,∠A=α,请猜想∠BOC=
(用α表示),并说明理由.
类比研究:
(3)BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线,它们交于点O,∠CBO=∠DBC,∠BCO=∠ECB,∠A=α,请猜想∠BOC=
.
《与三角形有关的线段和角》单元测试卷
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)下列各图中,正确画出AC边上的高的是( )
A.
B.
C.
D.
【分析】根据三角形高的定义,过点B与AC边垂直,且垂足在边AC上,然后结合各选项图形解答.
【解答】解:根据三角形高线的定义,只有D选项中的BE是边AC上的高.
故选:D.
【点评】本题主要考查了三角形的高线的定义,熟记定义并准确识图是解题的关键.
2.(3分)下列长度的三根小木棒能构成三角形的是( )
A.2cm,3cm,5cm
B.7cm,4cm,2cm
C.3cm,4cm,8cm
D.3cm,3cm,4cm
【分析】依据三角形任意两边之和大于第三边求解即可.
【解答】解:A、因为2+3=5,所以不能构成三角形,故A错误;
B、因为2+4<7,所以不能构成三角形,故B错误;
C、因为3+4<8,所以不能构成三角形,故C错误;
D、因为3+3>4,所以能构成三角形,故D正确.
故选:D.
【点评】本题主要考查的是三角形的三边关系,掌握三角形的三边关系是解题的关键.
3.(3分)下列图形中有稳定性的是( )
A.正方形
B.长方形
C.直角三角形
D.平行四边形
【分析】稳定性是三角形的特性.
【解答】解:根据三角形具有稳定性,可得四个选项中只有直角三角形具有稳定性.
故选:C.
【点评】稳定性是三角形的特性,这一点需要记忆.
4.(3分)在△ABC中,若∠A=95°,∠B=40°,则∠C的度数为( )
A.35°
B.40°
C.45°
D.50°
【分析】在△ABC中,根据三角形内角和是180度来求∠C的度数.
【解答】解:∵三角形的内角和是180°,
又∠A=95°,∠B=40°
∴∠C=180°﹣∠A﹣∠B
=180°﹣95°﹣40°
=45°,
故选:C.
【点评】本题考查了三角形内角和定理,利用三角形内角和定理:三角形内角和是180°是解答此题的关键.
5.(3分)如图,AE是△ABC的中线,已知EC=6,DE=2,则BD的长为( )
A.2
B.3
C.4
D.6
【分析】根据三角形中线的定义可得BE=EC=6,再根据BD=BE﹣DE即可求解.
【解答】解:∵AE是△ABC的中线,EC=6,
∴BE=EC=6,
∵DE=2,
∴BD=BE﹣DE=6﹣2=4.
故选:C.
【点评】本题考查了三角形的中线的定义,是基础题,准确识图并熟记中线的定义是解题的关键.
6.(3分)如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=( )
A.35°
B.95°
C.85°
D.75°
【分析】根据三角形角平分线的性质求出∠ACD,根据三角形外角性质求出∠A即可.
【解答】解:∵CE是△ABC的外角∠ACD的平分线,∠ACE=60°,
∴∠ACD=2∠ACE=120°,
∵∠ACD=∠B+∠A,
∴∠A=∠ACD﹣∠B=120°﹣35°=85°,
故选:C.
【点评】本题考查了三角形外角性质,角平分线定义的应用,注意:三角形的一个外角等于和它不相邻的两个内角的和.
7.(3分)如图,CD,CE,CF分别是△ABC的高、角平分线、中线,则下列各式中错误的是( )
A.AB=2BF
B.∠ACE=∠ACB
C.AE=BE
D.CD⊥BE
【分析】从三角形的一个顶点向对边作垂线,垂足与顶点之间的线段叫做三角形的高.
三角形一个内角的平分线与这个内角的对边交于一点,则这个内角的顶点与所交的点间的线段叫做三角形的角平分线.
三角形一边的中点与此边所对顶点的连线叫做三角形的中线.依此即可求解.
【解答】解:∵CD,CE,CF分别是△ABC的高、角平分线、中线,
∴CD⊥BE,∠ACE=∠ACB,AB=2BF,无法确定AE=BE.
故选:C.
【点评】考查了三角形的角平分线、中线和高,根据是熟悉它们的定义和性质.
8.(3分)如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC=( )
A.118°
B.119°
C.120°
D.121°
【分析】由三角形内角和定理得∠ABC+∠ACB=120°,由角平分线的性质得∠CBE+∠BCD=60°,再利用三角形的内角和定理得结果.
【解答】解:∵∠A=60°,
∴∠ABC+∠ACB=120°,
∵BE,CD是∠B、∠C的平分线,
∴∠CBE=∠ABC,∠BCD=,
∴∠CBE+∠BCD=(∠ABC+∠BCA)=60°,
∴∠BFC=180°﹣60°=120°,
故选:C.
【点评】本题主要考查了三角形内角和定理和角平分线的性质,综合运用三角形内角和定理和角平分线的性质是解答此题的关键.
9.(3分)若一个三角形的三条边长分别为3,2a﹣1,6,则整数a的值可能是( )
A.2,3
B.3,4
C.2,3,4
D.3,4,5
【分析】直接利用三角形三边关系得出a的取值范围,进而得出答案.
【解答】解:∵一个三角形的三条边长分别为3,2a﹣1,6,
∴,
解得:2<a<5,
故整数a的值可能是:3,4.
故选:B.
【点评】此题主要考查了三角形三边关系,正确得出a的取值范围是解题关键.
10.(3分)如图,已知AF平分∠BAC,过F作FD⊥BC,若∠B比∠C大20度,则∠F的度数是( )
A.10度
B.15度
C.20度
D.不能确定
【分析】根据题意可知∠B=20°+∠C,根据三角形的内角和定理可知∠ADC+∠DAC+∠C=180°,∠ADC=∠B+∠BAF,根据角平分线的性质,可知∠EAC=∠BAF,可得出∠ADC=100°,再根据FD⊥BC,可得出∠F的度数.
【解答】解:∵∠B比∠C大20度,
∴∠B=20°+∠C,
∵AF平分∠BAC,
∴∠EAC=∠BAF,
∵∠ADC+∠BAF+∠B﹣20°=180°,
∠ADC=∠B+∠BAF,
得出∠BAF+∠B=100°,
∴∠ADC=100°,
∵FD⊥BC,
∴∠ADC=90°+∠F=100°,
∴∠F=10°.
故选:A.
【点评】本题主要考查了三角形的内角和定理,角平分线的性质,以及三角形的外角等于与它不相邻的两内角和,比较综合,难度适中.
二.填空题(共8小题,满分24分,每小题3分)
11.(3分)如图,△ABC中,AD⊥BC于D,点E在CD上,则图中以AD为高的三角形有 6 个.
【分析】由于AD⊥BC于D,图中共有6个三角形,它们都有一边在直线CB上,由此即可确定以AD为高的三角形的个数.
【解答】解:∵AD⊥BC于D,
而图中有一边在直线CB上,且以A为顶点的三角形有6个,
∴以AD为高的三角形有6个.
故答案为:6.
【点评】此题主要考查了三角形的高,三角形的高可以在三角形外,可以是三角形的边,也可以在三角形内,所以确定三角形的高比较灵活.
12.(3分)如图,生活中都把自行车的几根梁做成三角形的支架,这是因为三角形具有 稳定 性.
【分析】根据三角形具有稳定性解答.
【解答】解:生活中都把自行车的几根梁做成三角形的支架,这是因为三角形具有稳定性.
故答案为:稳定.
【点评】本题考查三角形稳定性的实际应用.三角形的稳定性在实际生活中有着广泛的应用,如钢架桥、房屋架梁等,因此要使一些图形具有稳定的结构,往往通过连接辅助线转化为三角形而获得.
13.(3分)已知等腰三角形的两边长分别为4cm和8cm,则此三角形的周长为 20 cm.
【分析】根据等腰三角形的性质,本题要分情况讨论.当腰长为4cm或是腰长为8cm两种情况.
【解答】解:等腰三角形的两边长分别为4cm和8cm,
当腰长是4cm时,则三角形的三边是4cm,4cm,8cm,4cm+4cm=8cm不满足三角形的三边关系;
当腰长是8cm时,三角形的三边是8cm,8cm,4cm,三角形的周长是20cm.
故填20.
【点评】本题考查了等腰三角形的性质和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,进行分类讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.
14.(3分)将一副三角尺按如图所示的方式放置,使含30°角的三角尺的短直角边和含45°角的三角尺的一条直角边重合,则∠1的度数是 75° .
【分析】根据含30°角的三角尺的短直角边和含45°角的三角尺的一条直角边重合,得出平行线,再利用平行线的性质和对顶角相等得出∠2=45°,再利用三角形的外角性质解答即可.
【解答】解:如图,
∵含30°角的三角尺的短直角边和含45°角的三角尺的一条直角边重合,
∴AB∥CD,
∴∠3=∠4=45°,
∴∠2=∠3=45°,
∵∠B=30°,
∴∠1=∠2+∠B=30°+45°=75°,
故答案为:75°.
【点评】此题考查三角形外角性质,关键是利用平行线性质和对顶角相等得出∠2的度数.
15.(3分)已知a、b、c为△ABC的三边,化简:|a+b﹣c|+|a﹣b﹣c|﹣|a﹣b+c|= ﹣a+3b﹣c .
【分析】根据三角形三边关系:两边之和大于第三边,两边之差小于第三边,来判定绝对值里的式子的正负值,然后去绝对值进行计算即可.
【解答】解:|a+b﹣c|+|a﹣b﹣c|﹣|a﹣b+c|,
=(a+b﹣c)+(﹣a+b+c)﹣(a﹣b+c),
=a+b﹣c﹣a+b+c﹣a+b﹣c,
=﹣a+3b﹣c,
故答案为:﹣a+3b﹣c.
【点评】此题主要考查了三角形三边关系,以及绝对值的性质,关键是掌握三边关系定理.
16.(3分)如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=30°,∠2=20°,则∠B= 50° .
【分析】由AE平分∠BAC,可得角相等,由∠1=30°,∠2=20°,可求得∠EAD的度数,在直角三角形ABD在利用两锐角互余可求得答案.
【解答】解:∵AE平分∠BAC,
∴∠1=∠EAD+∠2,
∴∠EAD=∠1﹣∠2=30°﹣20°=10°,
Rt△ABD中,∠B=90°﹣∠BAD
=90°﹣30°﹣10°=50°.
故答案为50°.
【点评】本题考查了三角形的角平分线、中线和高的相关知识;求得∠EAD=10°是正确解答本题的关键.
17.(3分)当三角形中一个内角α是另一个内角β的一半时,我们称此三角形为“半角三角形”,其中α称为“半角”.如果一个“半角三角形”的“半角”为20°,那么这个“半角三角形”的最大内角的度数为 120° .
【分析】根据半角三角形的定义得出β的度数,再由三角形内角和定理求出另一个内角即可.
【解答】解:∵α=20°,
∴β=2α=40°,
∴最大内角的度数=180°﹣20°﹣40°=120°.
故答案为:120°.
【点评】本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.
18.(3分)如图,△ABC三边的中线AD、BE、CF的公共点为G,若S△ABC=12,则图中阴影部分的面积是 4 .
【分析】根据三角形的中线把三角形的面积分成相等的两部分,知△ABC的面积即为阴影部分的面积的3倍.
【解答】方法1
解:∵△ABC的三条中线AD、BE,CF交于点G,
∴S△CGE=S△AGE=S△ACF,S△BGF=S△BGD=S△BCF,
∵S△ACF=S△BCF=S△ABC=×12=6,
∴S△CGE=S△ACF=×6=2,S△BGF=S△BCF=×6=2,
∴S阴影=S△CGE+S△BGF=4.
故答案为4.
方法2
设△AFG,△BFG,△BDG,△CDG,△CEG,△AEG的面积分别为S1,S2,S3,S4,S5,S6,根据中线平分三角形面积可得:S1=S2,S3=S4,S5=S6,S1+S2+S3=S4+S5+S6①,S2+S3+S4=S1+S5+S6②
由①﹣②可得S1=S4,所以S1=S2=S3=S4=S5=S6=2,故阴影部分的面积为4.
故答案为:4.
【点评】根据三角形的中线把三角形的面积分成相等的两部分,该图中,△BGF的面积=△BGD的面积=△CGD的面积,△AGF的面积=△AGE的面积=△CGE的面积.
三.解答题(共7小题,满分66分)
19.(9分)已知△ABC(如图).
(1)画BC上的高;
(2)画∠B的平分线;
(3)画AB上的中线.
【分析】(1)过A作BC的垂线交CB的延长线于点D,则AD就是BC上的高;
(2)作∠ABC的平分线交AC于点E,则BE就是∠B的平分线;
(3)先作AB的垂直平分线,得到AB的中点是F,连接CF,则CF就是AB上的中线.
【解答】解:(1)①以点A为圆心,以适当长度(只要与CB的延长线有两个交点即可)为半径,画弧交CB的延长线于两点,
②以两个交点为圆心,以大于两点之间距离的一半为半径画弧,两弧交于一点,
③过点A与交点作直线与CB的延长线相交于点D,
则AD就是所要求作的BC上的高;
(2)①以点B为圆心,以任意长为半径画弧,分别于BA、BC边相交,
②分别以两交点为圆心,以大于两交点之间的距离的一半为半径画弧,两弧相交于一点,
连接点B与交点,交AC于点E,
则BE就是所要求作的∠B的平分线;
(3)①分别以点A、B为圆心,以大于AB为半径画弧,两弧相交于两点,
②连接这两个交点,交AB于点F,
③连接CF,
则CF就是所要求作的AB上的中线.
【点评】本题考查了过直线外一点作已知直线的作法,角平分线的作法,线段垂直平分线的作法,都是基本作图,需要熟练掌握.
20.(8分)如图,在△BCD中,BC=4,BD=5,
(1)求CD的取值范围;
(2)若AE∥BD,∠A=55°,∠BDE=125°,求∠C的度数.
【分析】(1)利用三角形三边关系得出DC的取值范围即可;
(2)利用平行线的性质得出∠AEC的度数,再利用三角形内角和定理得出答案.
【解答】解:(1)∵在△BCD中,BC=4,BD=5,
∴1<DC<9;
(2)∵AE∥BD,∠BDE=125°,
∴∠AEC=55°,
又∵∠A=55°,
∴∠C=70°.
【点评】此题主要考查了三角形三边关系以及平行线的性质,得出∠AEC的度数是解题关键.
21.(8分)如图,D是△ABC的BC边上的一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°.
(1)求∠B的度数.
(2)求∠C的度数.
【分析】(1)先由三角形外角的性质得出∠ADC=∠B+∠BAD,再由∠ADC=80°,∠B=∠BAD即可得出∠B的度数;
(2)直接根据三角形的内角和定理得出∠C的度数.
【解答】解:(1)∵∠ADC是△ABD的一个外角,
∴∠ADC=∠B+∠BAD,
又∵∠ADC=80°,∠B=∠BAD,
∴∠B=∠ADC=×80°=40°;
(2)在△ABC
中,
∵∠BAC+∠B+∠C=180°,
∴∠C=180°﹣∠B﹣∠BAC=180°﹣40°﹣70°=70°.
【点评】本题考查的是三角形内角和定理及外角的性质,熟知三角形的内角和是180°是解答此题的关键.
22.(10分)如图,在△ACB中,∠ACB=90゜,CD⊥AB于D.
(1)求证:∠ACD=∠B;
(2)若AF平分∠CAB分别交CD、BC于E、F,求证:∠CEF=∠CFE.
【分析】(1)由于∠ACD与∠B都是∠BCD的余角,根据同角的余角相等即可得证;
(2)根据直角三角形两锐角互余得出∠CFA=90°﹣∠CAF,∠AED=90°﹣∠DAE,再根据角平分线的定义得出∠CAF=∠DAE,然后由对顶角相等的性质,等量代换即可证明∠CEF=∠CFE.
【解答】证明:(1)∵∠ACB=90゜,CD⊥AB于D,
∴∠ACD+∠BCD=90°,∠B+∠BCD=90°,
∴∠ACD=∠B;
(2)在Rt△AFC中,∠CFA=90°﹣∠CAF,
同理在Rt△AED中,∠AED=90°﹣∠DAE.
又∵AF平分∠CAB,
∴∠CAF=∠DAE,
∴∠AED=∠CFE,
又∵∠CEF=∠AED,
∴∠CEF=∠CFE.
【点评】本题考查了直角三角形的性质,三角形角平分线的定义,对顶角的性质,余角的性质,难度适中.
23.(9分)如图:△ABC纸片沿DE折叠,使点A落在四边形BCDE的内部.∠A与∠1+∠2之间存在怎样的数量关系?为什么?
【分析】本题可根据四边形的内角和为360°及翻折的性质,就可求出2∠A=∠1+∠2这一始终保持不变的性质.
【解答】解:2∠A=∠1+∠2,
理由:∵在四边形ADA′E中,∠A+∠A′+∠ADA′+∠AEA′=360°,
则2∠A+180°﹣∠2+180°﹣∠1=360°,
∴可得2∠A=∠1+∠2.
【点评】本题主要考查四边形的内角和及翻折的性质特点,解决本题的关键是熟记翻折的性质.
24.(10分)如图,O是△ABC内任意一点,连接OB、OC.
(1)求证:∠BOC>∠A;
(2)比较AB+AC与OB+OC的大小,并说明理由.
【分析】(1)延长BO交AC于点D,首先利用三角形的外角性质得到∠BOC>∠ODC,让根据∠ODC>∠A,证得∠BOC>∠A;
(2)根据三角形的三边关系证得AB+AD>OB+OD,OD+CD>OC,从而得到AB+AD+CD>OB+OC,进而得到AB+AC>OB+OC.
【解答】解:(1)证明:延长BO交AC于点D,
∴∠BOC>∠ODC,
又∠ODC>∠A,
∴∠BOC>∠A;
(2)AB+AC>OB+OC,
∵AB+AD>OB+OD,OD+CD>OC,
∴AB+AD+CD>OB+OC,
即:AB+AC>OB+OC.
【点评】本题考出了三角形的三边关系及三角形的外角的性质,解题的关键是能够正确的构造三角形,难度不大.
25.(12分)问题引入:
(1)如图①,在△ABC中,点O是∠ABC和∠ACB平分线的交点,若∠A=α,则∠BOC= 90°+α (用α表示);如图②,∠CBO=∠ABC,∠BCO=∠ACB,∠A=α,则∠BOC= 120°+α (用α表示)
拓展研究:
(2)如图③,∠CBO=∠DBC,∠BCO=∠ECB,∠A=α,请猜想∠BOC= 120°﹣α (用α表示),并说明理由.
类比研究:
(3)BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线,它们交于点O,∠CBO=∠DBC,∠BCO=∠ECB,∠A=α,请猜想∠BOC= ﹣α .
【分析】(1)如图①,根据角平分线的定义可得∠OBC=∠ABC,∠OCB=∠ACB,然后表示出∠OBC+∠OCB,再根据三角形的内角和等于180°列式整理即可得∠BOC=90°+α;如图②,根据三角形的内角和等于180°列式整理即可得∠BOC=120°+α;
(2)如图③,根据三角形的内角和等于180°列式整理即可得∠BOC=120°﹣α;
(3)根据三角形的内角和等于180°列式整理即可得∠BOC=﹣α.
【解答】解:(1)如图①,∵∠ABC与∠ACB的平分线相交于点O,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∴∠OBC+∠OCB=(∠ABC+∠ACB),
在△OBC中,∠BOC=180°﹣(∠OBC+∠OCB)
=180°﹣(∠ABC+∠ACB)
=180°﹣(180°﹣∠A)
=90°+∠A
=90°+α;
如图②,在△OBC中,∠BOC=180°﹣(∠OBC+∠OCB)
=180°﹣(∠ABC+∠ACB)
=180°﹣(180°﹣∠A)
=120°+∠A
=120°+α;
(2)如图③,在△OBC中,∠BOC=180°﹣(∠OBC+∠OCB)
=180°﹣(∠DBC+∠ECB)
=180°﹣(∠A+∠ACB+∠A+ABC)
=180°﹣(∠A+180°)
=120°﹣α;
(3)在△OBC中,∠BOC=180°﹣(∠OBC+∠OCB)
=180°﹣(∠DBC+∠ECB)
=180°﹣(∠A+∠ACB+∠A+ABC)
=180°﹣(∠A+180°)
=﹣α.
故答案为90°+α,120°+α;120°﹣α;﹣α.
【点评】本题考查了三角形的内角和定理,角平分线的定义,整体思想的利用是解题的关键.
第11题图
第12题图
第14题图
第16题图
第5题图
第6题图
第7题图
第8题图
第10题图
第18题图
第19题图
第20题图
第21题图
第22题图
第23题图
第24题图
第25题图
