2021-2022学年北师大版八上数学第1章 第1节探索勾股定理 课堂练习(word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版八上数学第1章 第1节探索勾股定理 课堂练习(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 220.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-04 20:41:09 | ||
图片预览

文档简介
北师大版八上数学
第1章
第1节
第1课时
探索勾股定理(1)
一、选择题(共4小题;共20分)
1.
一个直角三角形,两直角边的长分别为
和
,下列说法中正确的是
A.
斜边长为
B.
三角形的周长为
C.
斜边长为
D.
三角形的面积为
2.
如图,在三个正方形中,已知其中两个正方形的面积分别为
,,则第三个正方形的面积
为
A.
B.
C.
D.
3.
下列说法中正确的是
A.
若
,,
是
的三边,则
B.
若
,,
是
的三边,则
C.
若
,,
是
的三边,,则
D.
若
,,
是
的三边,,则
4.
如图,正方形
的面积为
,
为直角三角形,,且
,那么
的长为
A.
B.
C.
D.
不能确定
二、填空题(共10小题;共50分)
5.
直角三角形三边存在的关系:在直角三角形中,任意两条边确定了,另外一条边也就随之
?,三边之间存在着一个特定的
?关系.
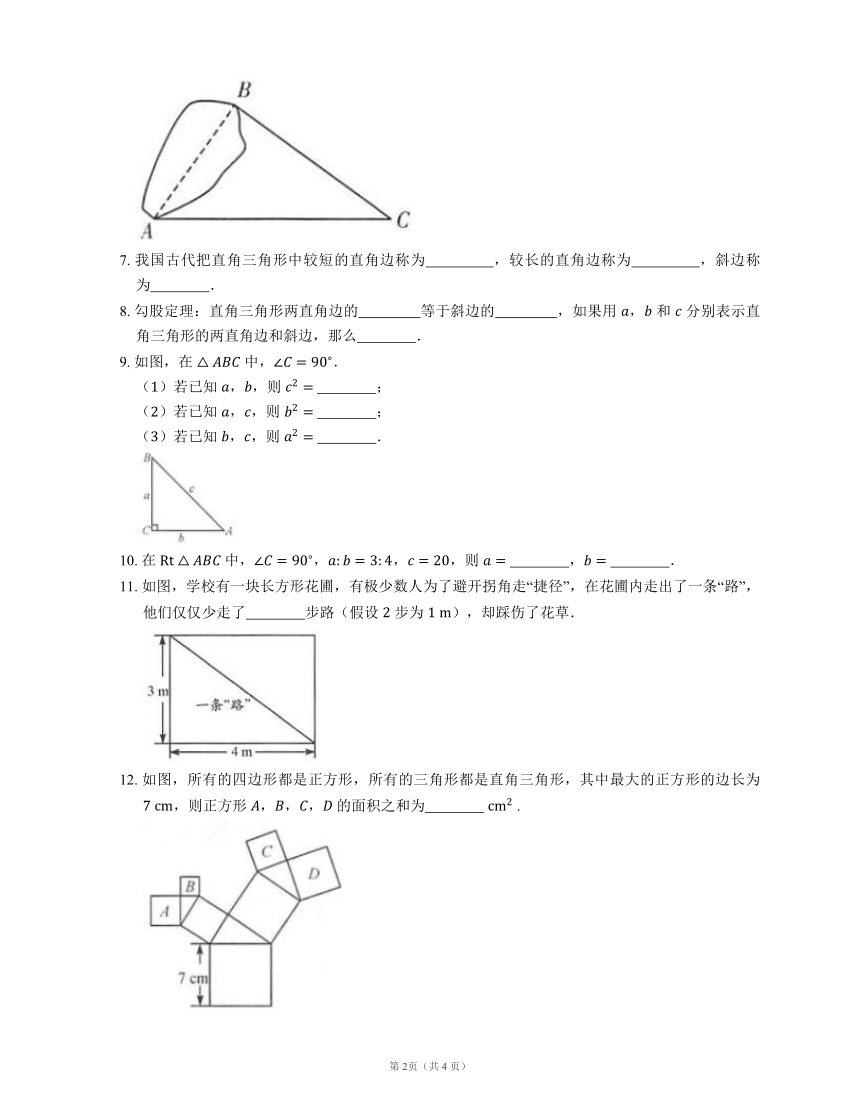
6.
如图,为了测得湖两岸点
和点
之间的距离,一个观测者在点
设桩,使
,并测得
,,则点
和点
之间的距离是
?.
7.
我国古代把直角三角形中较短的直角边称为
?,较长的直角边称为
?,斜边称为
?.
8.
勾股定理:直角三角形两直角边的
?等于斜边的
?,如果用
,
和
分别表示直角三角形的两直角边和斜边,那么
?.
9.
如图,在
中,.
()若已知
,,则
?;
()若已知
,,则
?;
()若已知
,,则
?.
10.
在
中,,,,则
?,
?.
11.
如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,他们仅仅少走了
?步路(假设
步为
),却踩伤了花草.
12.
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为
,则正方形
,,,
的面积之和为
?
.
13.
如果直角三角形的斜边与一条直角边的长分别是
和
,那么这个直角三角形的面积是
?
.
14.
如图,两个正方形的面积分别为
和
,则
?.
三、解答题(共3小题;共30分)
15.
求下列图形中未知边的长度
和未知正方形的面积
.
16.
有一架飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶正上方
处,过了
,飞机距离这个男孩头顶
,那么这架飞机每小时飞行多少千米?
17.
如图,在
中,,,,求
边上的高
的长.
答案
1.
C
2.
C
3.
D
4.
C
5.
确定,数量
6.
7.
勾,股,弦
8.
平方和,平方,
9.
,,
10.
,
11.
12.
13.
14.
15.
,.
16.
如图,
,,
故由勾股定理得
,
即
.
因为飞机
飞行
,
所以它每小时飞行的距离为
.
17.
设
,则
.
在
中,.
在
中,.
所以
.
解得
.
所以
.
第1页(共4
页)
第1章
第1节
第1课时
探索勾股定理(1)
一、选择题(共4小题;共20分)
1.
一个直角三角形,两直角边的长分别为
和
,下列说法中正确的是
A.
斜边长为
B.
三角形的周长为
C.
斜边长为
D.
三角形的面积为
2.
如图,在三个正方形中,已知其中两个正方形的面积分别为
,,则第三个正方形的面积
为
A.
B.
C.
D.
3.
下列说法中正确的是
A.
若
,,
是
的三边,则
B.
若
,,
是
的三边,则
C.
若
,,
是
的三边,,则
D.
若
,,
是
的三边,,则
4.
如图,正方形
的面积为
,
为直角三角形,,且
,那么
的长为
A.
B.
C.
D.
不能确定
二、填空题(共10小题;共50分)
5.
直角三角形三边存在的关系:在直角三角形中,任意两条边确定了,另外一条边也就随之
?,三边之间存在着一个特定的
?关系.
6.
如图,为了测得湖两岸点
和点
之间的距离,一个观测者在点
设桩,使
,并测得
,,则点
和点
之间的距离是
?.
7.
我国古代把直角三角形中较短的直角边称为
?,较长的直角边称为
?,斜边称为
?.
8.
勾股定理:直角三角形两直角边的
?等于斜边的
?,如果用
,
和
分别表示直角三角形的两直角边和斜边,那么
?.
9.
如图,在
中,.
()若已知
,,则
?;
()若已知
,,则
?;
()若已知
,,则
?.
10.
在
中,,,,则
?,
?.
11.
如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,他们仅仅少走了
?步路(假设
步为
),却踩伤了花草.
12.
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为
,则正方形
,,,
的面积之和为
?
.
13.
如果直角三角形的斜边与一条直角边的长分别是
和
,那么这个直角三角形的面积是
?
.
14.
如图,两个正方形的面积分别为
和
,则
?.
三、解答题(共3小题;共30分)
15.
求下列图形中未知边的长度
和未知正方形的面积
.
16.
有一架飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶正上方
处,过了
,飞机距离这个男孩头顶
,那么这架飞机每小时飞行多少千米?
17.
如图,在
中,,,,求
边上的高
的长.
答案
1.
C
2.
C
3.
D
4.
C
5.
确定,数量
6.
7.
勾,股,弦
8.
平方和,平方,
9.
,,
10.
,
11.
12.
13.
14.
15.
,.
16.
如图,
,,
故由勾股定理得
,
即
.
因为飞机
飞行
,
所以它每小时飞行的距离为
.
17.
设
,则
.
在
中,.
在
中,.
所以
.
解得
.
所以
.
第1页(共4
页)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
