2021-2022学年北师大版八上数学第1章 第3节 勾股定理的应用 课堂练习(word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版八上数学第1章 第3节 勾股定理的应用 课堂练习(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 146.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-04 20:44:58 | ||
图片预览

文档简介
北师大版八上数学
第1章
第3节
勾股定理的应用
一、选择题(共5小题;共20分)
1.
放学后,小林和小明从学校出发,分别沿东南方向和西南方向回家,他们行走的速度都是
,小林用了
到家,小明用了
到家,则他们两家之间的距离为
A.
B.
C.
D.
以上都不对
2.
一直角三角形的斜边比一直角边长
,另一直角边长为
,则斜边长为
A.
B.
C.
D.
3.
一只蚂蚁沿直角三角形的边爬行一周需
,若将直角三角形的边长均增加
倍,那么这只蚂蚁再沿直角三角形的边爬行一周需
A.
B.
C.
D.
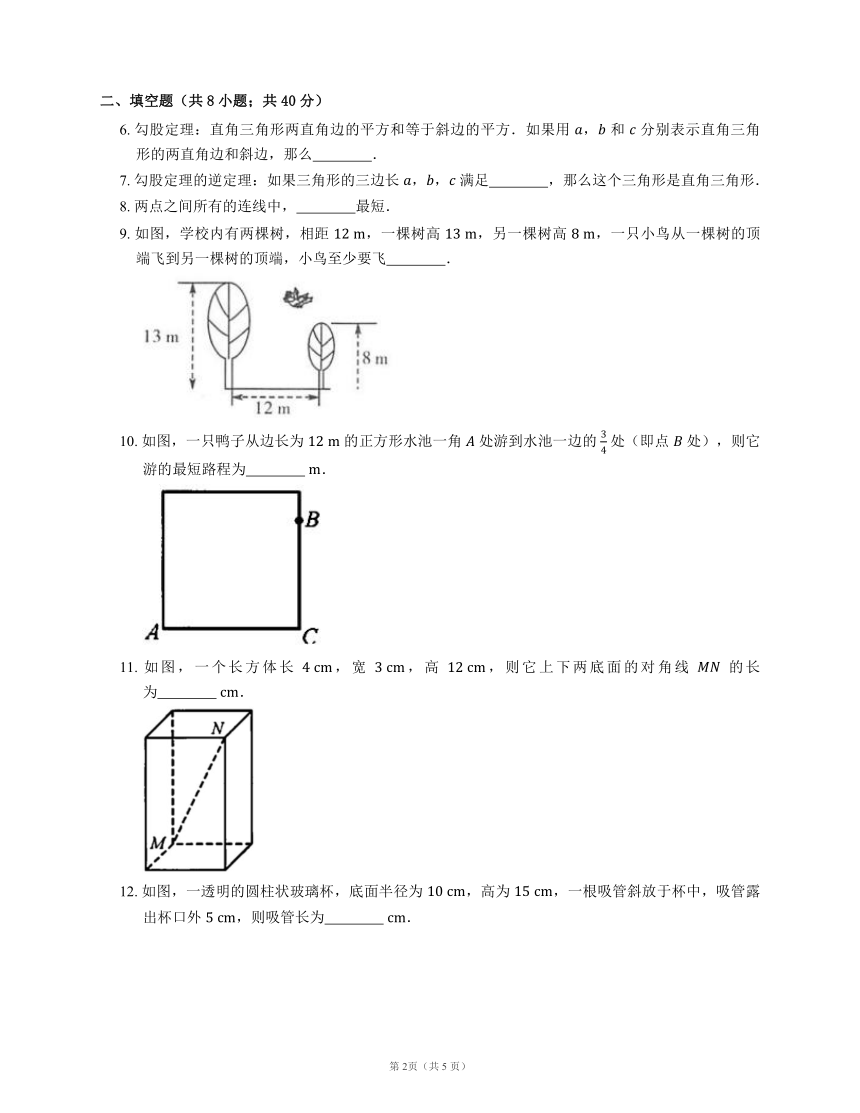
4.
如图所示,圆柱的高
,底面直径
,现在有一只蚂蚁想要从
处沿圆柱表面爬到对角
处捕食,则它爬行的最短距离是(
取
)
A.
B.
C.
D.
5.
如图是用
个全等的直角三角形与
个小正方形镶嵌而成的正方形图案,已知大正方形的面积为
,小正方形的面积为
,若用
,
表示直角三角形的两直角边(),请观察图案,指出以下关系式中不正确的是
A.
B.
C.
D.
二、填空题(共8小题;共40分)
6.
勾股定理:直角三角形两直角边的平方和等于斜边的平方.如果用
,
和
分别表示直角三角形的两直角边和斜边,那么
?.
7.
勾股定理的逆定理:如果三角形的三边长
,,
满足
?,那么这个三角形是直角三角形.
8.
两点之间所有的连线中,
?最短.
9.
如图,学校内有两棵树,相距
,一棵树高
,另一棵树高
,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞
?.
10.
如图,一只鸭子从边长为
的正方形水池一角
处游到水池一边的
处(即点
处),则它游的最短路程为
?
.
11.
如图,一个长方体长
,宽
,高
,则它上下两底面的对角线
的长为
?
.
12.
如图,一透明的圆柱状玻璃杯,底面半径为
,高为
,一根吸管斜放于杯中,吸管露出杯口外
,则吸管长为
?
.
13.
使用
长的梯子登上建筑物,如果梯子的底部与建筑物的底部的距离不能小于
,则使用该梯子最多可登上
?
高的建筑物.
三、解答题(共3小题;14,15题各13分,16题14分,共40分)
14.
如图,已知长方体的长为
,宽为
,高为
,一只蚂蚁如果沿长方体的表面从点
爬到点
,最短路程是多少?
15.
如图,有一个水池,水面是一个边长为
米的正方形,在水池正中央有一根芦苇,它高出水面
米.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.问这个水池的深度与这根芦苇的长度分别是多少?
16.
如图所示,某人到一个荒岛上去探宝,在
处登陆后,往东走
,又往北走
,遇到障碍后又往西走
,再折向北方走到
处往东一拐,仅
就找到了宝藏.问:登陆点(
处)到宝藏埋藏点(
处)的直线距离是多少?
答案
1.
C
2.
C
3.
A
4.
B
5.
D
6.
7.
8.
线段
9.
10.
11.
12.
13.
14.
.
15.
设水池的深度为
米,则芦苇的长度为
米,结合图形,
由勾股定理,得
,
即
.
解得
,这时
,
即水池的深度为
米,芦苇的长度为
米.
16.
千米.
第1页(共5
页)
第1章
第3节
勾股定理的应用
一、选择题(共5小题;共20分)
1.
放学后,小林和小明从学校出发,分别沿东南方向和西南方向回家,他们行走的速度都是
,小林用了
到家,小明用了
到家,则他们两家之间的距离为
A.
B.
C.
D.
以上都不对
2.
一直角三角形的斜边比一直角边长
,另一直角边长为
,则斜边长为
A.
B.
C.
D.
3.
一只蚂蚁沿直角三角形的边爬行一周需
,若将直角三角形的边长均增加
倍,那么这只蚂蚁再沿直角三角形的边爬行一周需
A.
B.
C.
D.
4.
如图所示,圆柱的高
,底面直径
,现在有一只蚂蚁想要从
处沿圆柱表面爬到对角
处捕食,则它爬行的最短距离是(
取
)
A.
B.
C.
D.
5.
如图是用
个全等的直角三角形与
个小正方形镶嵌而成的正方形图案,已知大正方形的面积为
,小正方形的面积为
,若用
,
表示直角三角形的两直角边(),请观察图案,指出以下关系式中不正确的是
A.
B.
C.
D.
二、填空题(共8小题;共40分)
6.
勾股定理:直角三角形两直角边的平方和等于斜边的平方.如果用
,
和
分别表示直角三角形的两直角边和斜边,那么
?.
7.
勾股定理的逆定理:如果三角形的三边长
,,
满足
?,那么这个三角形是直角三角形.
8.
两点之间所有的连线中,
?最短.
9.
如图,学校内有两棵树,相距
,一棵树高
,另一棵树高
,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞
?.
10.
如图,一只鸭子从边长为
的正方形水池一角
处游到水池一边的
处(即点
处),则它游的最短路程为
?
.
11.
如图,一个长方体长
,宽
,高
,则它上下两底面的对角线
的长为
?
.
12.
如图,一透明的圆柱状玻璃杯,底面半径为
,高为
,一根吸管斜放于杯中,吸管露出杯口外
,则吸管长为
?
.
13.
使用
长的梯子登上建筑物,如果梯子的底部与建筑物的底部的距离不能小于
,则使用该梯子最多可登上
?
高的建筑物.
三、解答题(共3小题;14,15题各13分,16题14分,共40分)
14.
如图,已知长方体的长为
,宽为
,高为
,一只蚂蚁如果沿长方体的表面从点
爬到点
,最短路程是多少?
15.
如图,有一个水池,水面是一个边长为
米的正方形,在水池正中央有一根芦苇,它高出水面
米.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.问这个水池的深度与这根芦苇的长度分别是多少?
16.
如图所示,某人到一个荒岛上去探宝,在
处登陆后,往东走
,又往北走
,遇到障碍后又往西走
,再折向北方走到
处往东一拐,仅
就找到了宝藏.问:登陆点(
处)到宝藏埋藏点(
处)的直线距离是多少?
答案
1.
C
2.
C
3.
A
4.
B
5.
D
6.
7.
8.
线段
9.
10.
11.
12.
13.
14.
.
15.
设水池的深度为
米,则芦苇的长度为
米,结合图形,
由勾股定理,得
,
即
.
解得
,这时
,
即水池的深度为
米,芦苇的长度为
米.
16.
千米.
第1页(共5
页)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
