第一章 勾股定理单元质量检测试卷C(含解析)
文档属性
| 名称 | 第一章 勾股定理单元质量检测试卷C(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-03 22:02:18 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
北师大版2021-2022学年八年级(上)第一章勾股定理检测试卷C
(时间120分钟,满分120分)
一、选择题(共12小题;每小题3分,共36分)
1.
校园内有两棵树,相距
米,一棵树高
米,另一棵树高
米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,则小鸟至少要飞
A.
米
B.
米
C.
米
D.
米
2.
如图,
中,,,,将
沿
翻折,使点
与点
重合,则
的长为
A.
B.
C.
D.
3.
如图,长为
的橡皮筋放置在
轴上,固定两端
和
,然后把中点
向上拉升
至
点,则橡皮筋被拉长了
A.
B.
C.
D.
4.
下列各组数中不能作为直角三角形的三边长的是
A.
,,
B.
,,
C.
,,
D.
,,
5.
如图,在
中,,,,将
折叠,使点
与
的中点
重合,折痕交
于点
,交
于点
,则线段
的长为
A.
B.
C.
D.
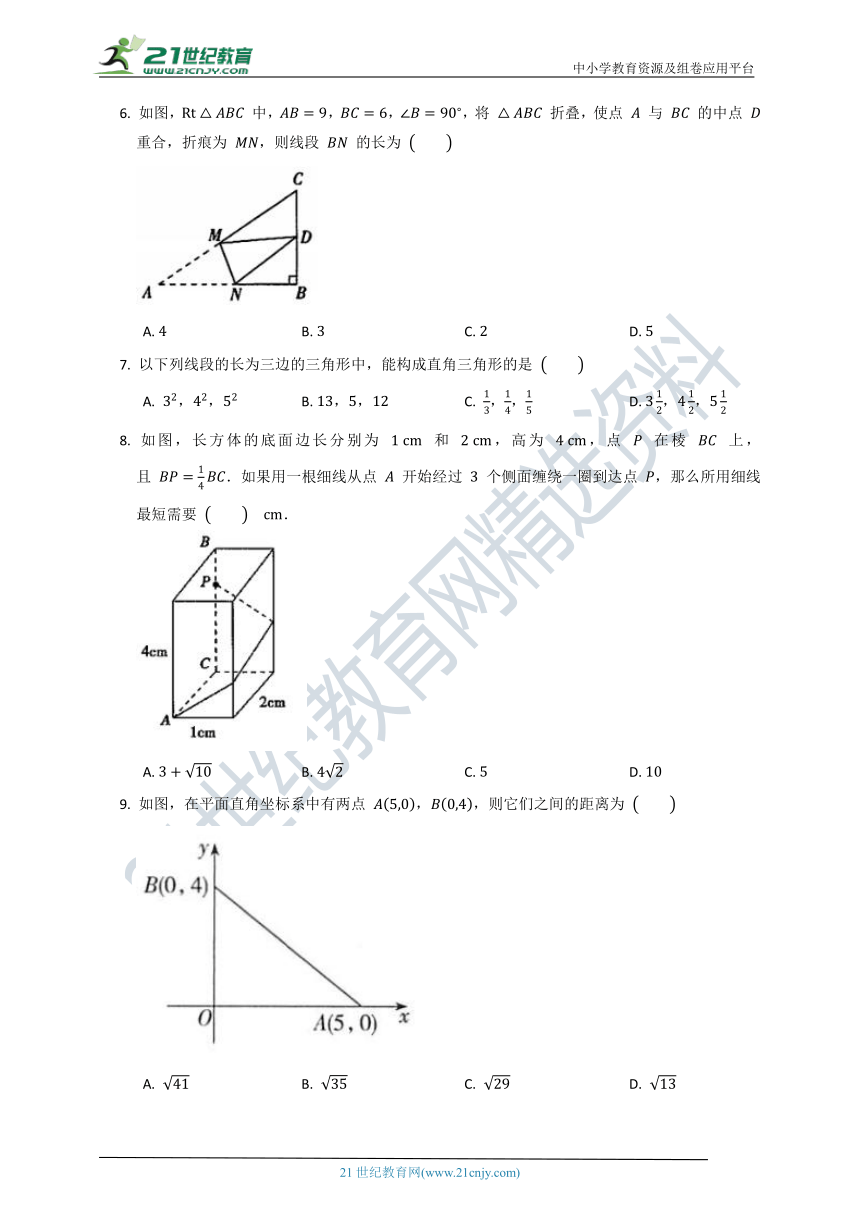
6.
如图,
中,,,,将
折叠,使点
与
的中点
重合,折痕为
,则线段
的长为
A.
B.
C.
D.
7.
以下列线段的长为三边的三角形中,能构成直角三角形的是
A.
,,
B.
,,
C.
,,
D.
,,
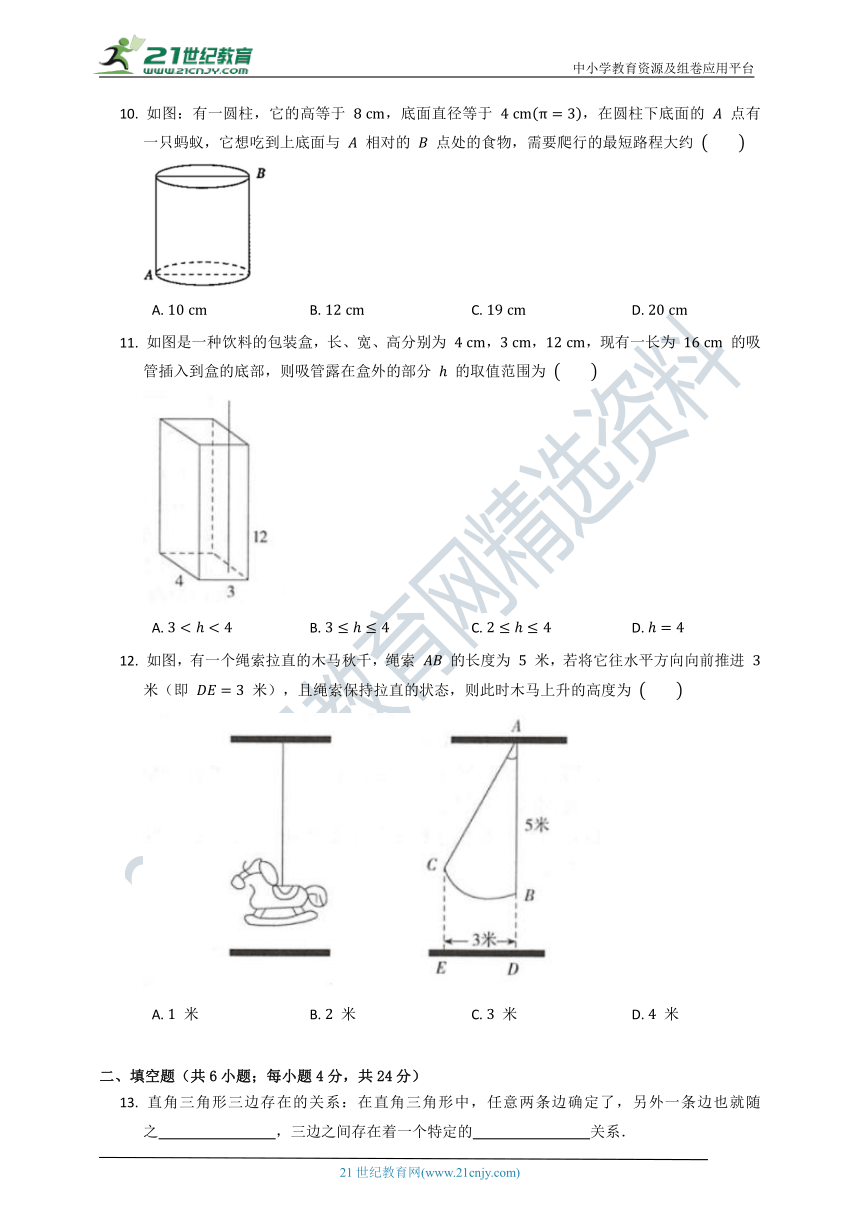
8.
如图,长方体的底面边长分别为
和
,高为
,点
在棱
上,且
.如果用一根细线从点
开始经过
个侧面缠绕一圈到达点
,那么所用细线最短需要
.
A.
B.
C.
D.
9.
如图,在平面直角坐标系中有两点
,,则它们之间的距离为
A.
B.
C.
D.
10.
如图:有一圆柱,它的高等于
,底面直径等于
,在圆柱下底面的
点有一只蚂蚁,它想吃到上底面与
相对的
点处的食物,需要爬行的最短路程大约
A.
B.
C.
D.
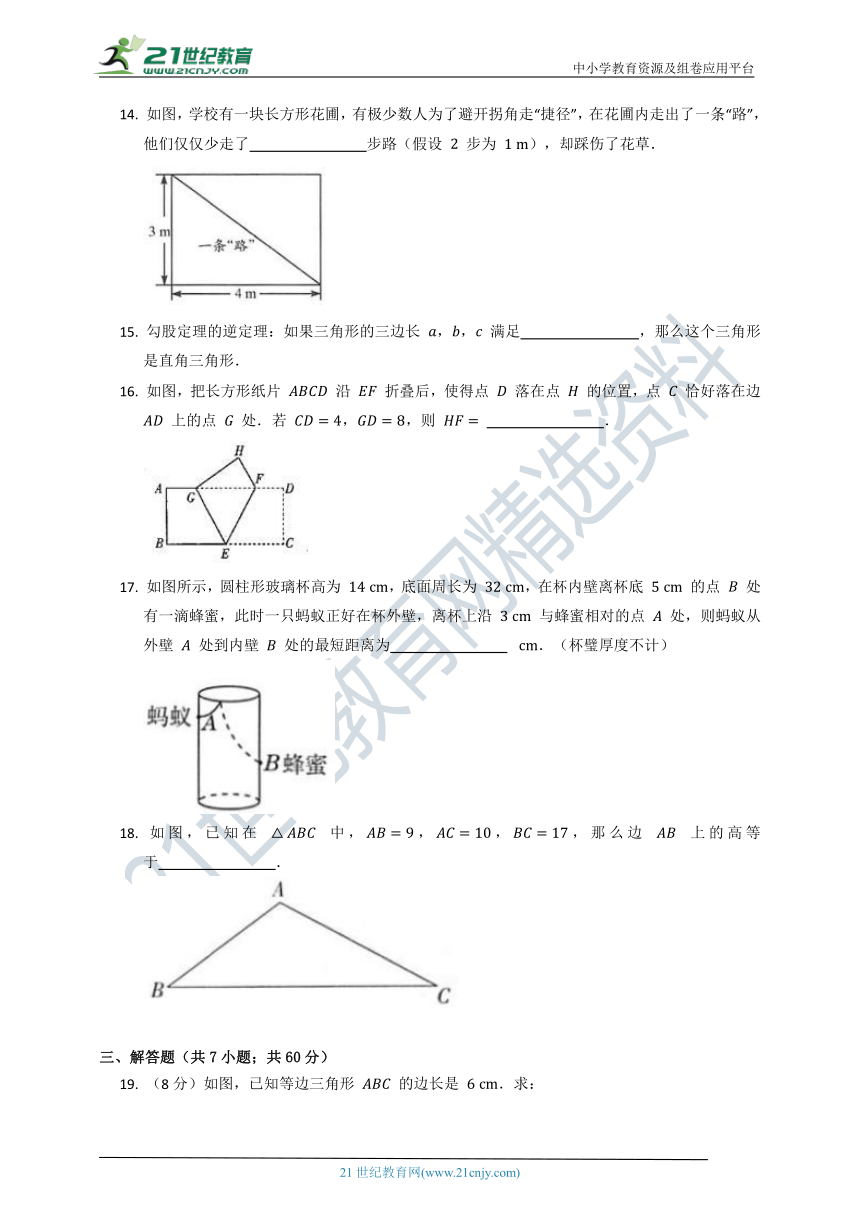
11.
如图是一种饮料的包装盒,长、宽、高分别为
,,,现有一长为
的吸管插入到盒的底部,则吸管露在盒外的部分
的取值范围为
A.
B.
C.
D.
12.
如图,有一个绳索拉直的木马秋千,绳索
的长度为
米,若将它往水平方向向前推进
米(即
米),且绳索保持拉直的状态,则此时木马上升的高度为
A.
米
B.
米
C.
米
D.
米
二、填空题(共6小题;每小题4分,共24分)
13.
直角三角形三边存在的关系:在直角三角形中,任意两条边确定了,另外一条边也就随之
?,三边之间存在着一个特定的
?关系.
14.
如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,他们仅仅少走了
?步路(假设
步为
),却踩伤了花草.
15.
勾股定理的逆定理:如果三角形的三边长
,,
满足
?,那么这个三角形是直角三角形.
16.
如图,把长方形纸片
沿
折叠后,使得点
落在点
的位置,点
恰好落在边
上的点
处.若
,,则
?.
17.
如图所示,圆柱形玻璃杯高为
,底面周长为
,在杯内壁离杯底
的点
处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿
与蜂蜜相对的点
处,则蚂蚁从外壁
处到内壁
处的最短距离为
?
.(杯璧厚度不计)
18.
如图,已知在
中,,,,那么边
上的高等于
?.
三、解答题(共7小题;共60分)
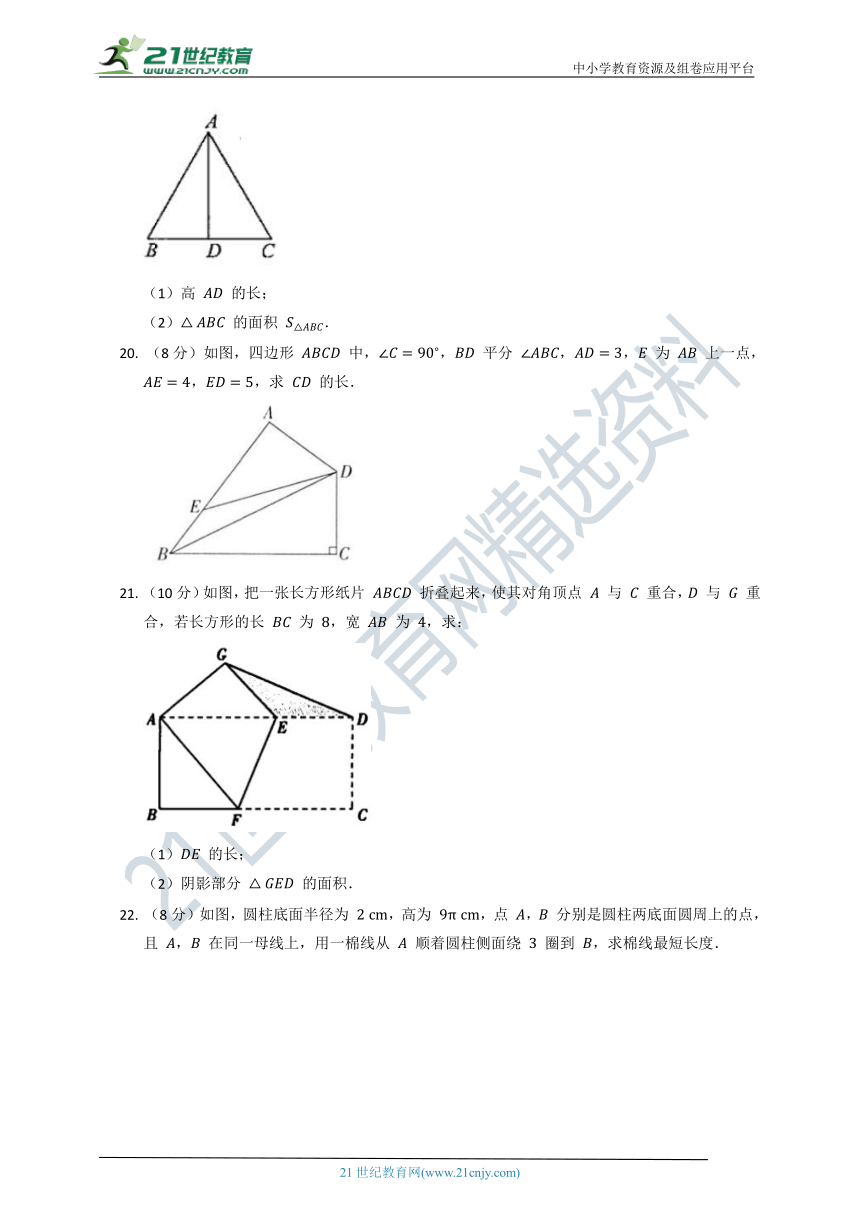
19.
(8分)如图,已知等边三角形
的边长是
.求:
(1)高
的长;
(2)
的面积
.
20.
(8分)如图,四边形
中,,
平分
,,
为
上一点,,,求
的长.
21.
(10分)如图,把一张长方形纸片
折叠起来,使其对角顶点
与
重合,
与
重合,若长方形的长
为
,宽
为
,求:
(1)
的长;
(2)阴影部分
的面积.
22.
(8分)如图,圆柱底面半径为
,高为
,点
,
分别是圆柱两底面圆周上的点,且
,
在同一母线上,用一棉线从
顺着圆柱侧面绕
圈到
,求棉线最短长度.
23.
(8分)一块
的长方形吹塑纸板,按照如图所示的方式设计构图,做新冠疫情防控宣传展板,若在
,
两点之间贴一条彩色胶带,则彩色胶带的长至少是多少米?
24.(8分)
如图,,,
是直线
上的三个点,
于点
,
于点
,且
,,,,求
的长.
25.(10分)
在
中,,,,
是
内部一点,且点
到各边的距离相等,求这个距离.
答案
第一部分
1.
A
【解析】如图所示,
,
为树,且
米,
米,
米.过
作
于
,则
米,
米,
在直角三角形
中,由勾股定理得
米,
故小鸟至少要飞
米.
2.
D
【解析】设
,则
,
在
中,,
即
,
解得
.
3.
A
【解析】在
中,
,,
根据勾股定理得
,
.
故橡皮筋被拉长了
,故选A.
4.
B
【解析】A.
,
以
,,
为边能组成直角三角形,故本选项不符合题意;
B.
,
以
,,
为边不能组成直角三角形,故本选项符合题意;
C.
,
以
,,
为边能组成直角三角形,故本选项不符合题意;
D.
,
以
,,
为边能组成直角三角形,故本选项不符合题意.
故选B.
5.
D
【解析】
是
中点,,
,
折叠,
,
,
在
中,,
,
,
.
6.
A
【解析】设
,由折叠可得
,
是
的中点,
,
在
中,,
解得
,即
.
7.
B
【解析】A.,不能构成直角三角形;
B.,能构成直角三角形;
C.,不能构成直角三角形;
D.,不能构成直角三角形.故选B.
8.
C
【解析】将长方体展开,连接
,
长方体的底面边长分别为
和
,高为
,点
在边
上,且
,
,,根据两点之间线段最短,.
9.
A
【解析】,,
,,
,
即这两点之间的距离是
.故选A.
10.
A
11.
B
【解析】①当吸管放进包装盒且垂直于包装盒底面时露在盒外的长度最长,最长为
.
②
露出部分最短时,包装盒内的吸管与底面对角线和高正好组成直角三角形,
底面对角线长为
,高为
.设包装盒里吸管长为
,
则
,
所以
,
所以露在包装盒外的吸管的长度最短为
.
则吸管露在盒外的部分
的取值范围为
.故选B.
12.
A
【解析】如图,过点
作
于点
,
根据题意,得
米,
米,
在
中,由勾股定理,得
,
,
米,
米.
此时木马上升的高度为
米,故选A.
第二部分
13.
确定,数量
14.
15.
16.
17.
【解析】如图所示,圆柱形玻璃杯的侧面展开图的一半为
,作点
关于
的对称点
,连接
,过点
作
,垂足为点
,
根据题意得
,,
所以
,.
因为
,
所以
,
即从外壁
处到内壁
处的最短距离为
.
18.
【解析】如图,作
,交
边的延长线于
点,
设
,,
在直角
中,,
在直角
中,,
,即
,
由①②得
,,即
,
为
边上的高,
边上的高等于
.
第三部分
19.
(1)
??????(2)
20.
,,,
,
,
.
,
.
平分
,
.
21.
(1)
设
,则
,
在
中,,
,
解得
,
.
??????(2)
过
点作
于
,
则
,
,,,
,
.
22.
圆柱体的展开图如图所示,
用一棉线从
顺着圆柱侧面绕
圈到
的运动最短路线是:,即在圆柱体的展开图长方形中,将长方形平均分成
个小长方形,
沿着
个小长方形的对角线运动到
的路线最短.
圆柱底面半径为
,
长方形的宽即是圆柱体的底面圆的周长为
.
又圆柱高为
,
小长方体的一条边长是
.
根据勾股定理求得
.
.
故棉线的最短长度为
.
23.
过点
作
于
,如图,
从图中可以看出
,
,
在直角
中,
为斜边,
则
.
答:彩色胶带的长至少是
.
24.
设
,则
,
于点
,
于点
,
和
都是直角三角形,
在
中,,
在
中,,
,
,
即
,
解得
,
即
的长为
.
25.
设点
到
各边距离都为
.
因为
,,,
,
所以
是直角三角形.
所以
.
因为
,
所以
.解得
.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
北师大版2021-2022学年八年级(上)第一章勾股定理检测试卷C
(时间120分钟,满分120分)
一、选择题(共12小题;每小题3分,共36分)
1.
校园内有两棵树,相距
米,一棵树高
米,另一棵树高
米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,则小鸟至少要飞
A.
米
B.
米
C.
米
D.
米
2.
如图,
中,,,,将
沿
翻折,使点
与点
重合,则
的长为
A.
B.
C.
D.
3.
如图,长为
的橡皮筋放置在
轴上,固定两端
和
,然后把中点
向上拉升
至
点,则橡皮筋被拉长了
A.
B.
C.
D.
4.
下列各组数中不能作为直角三角形的三边长的是
A.
,,
B.
,,
C.
,,
D.
,,
5.
如图,在
中,,,,将
折叠,使点
与
的中点
重合,折痕交
于点
,交
于点
,则线段
的长为
A.
B.
C.
D.
6.
如图,
中,,,,将
折叠,使点
与
的中点
重合,折痕为
,则线段
的长为
A.
B.
C.
D.
7.
以下列线段的长为三边的三角形中,能构成直角三角形的是
A.
,,
B.
,,
C.
,,
D.
,,
8.
如图,长方体的底面边长分别为
和
,高为
,点
在棱
上,且
.如果用一根细线从点
开始经过
个侧面缠绕一圈到达点
,那么所用细线最短需要
.
A.
B.
C.
D.
9.
如图,在平面直角坐标系中有两点
,,则它们之间的距离为
A.
B.
C.
D.
10.
如图:有一圆柱,它的高等于
,底面直径等于
,在圆柱下底面的
点有一只蚂蚁,它想吃到上底面与
相对的
点处的食物,需要爬行的最短路程大约
A.
B.
C.
D.
11.
如图是一种饮料的包装盒,长、宽、高分别为
,,,现有一长为
的吸管插入到盒的底部,则吸管露在盒外的部分
的取值范围为
A.
B.
C.
D.
12.
如图,有一个绳索拉直的木马秋千,绳索
的长度为
米,若将它往水平方向向前推进
米(即
米),且绳索保持拉直的状态,则此时木马上升的高度为
A.
米
B.
米
C.
米
D.
米
二、填空题(共6小题;每小题4分,共24分)
13.
直角三角形三边存在的关系:在直角三角形中,任意两条边确定了,另外一条边也就随之
?,三边之间存在着一个特定的
?关系.
14.
如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,他们仅仅少走了
?步路(假设
步为
),却踩伤了花草.
15.
勾股定理的逆定理:如果三角形的三边长
,,
满足
?,那么这个三角形是直角三角形.
16.
如图,把长方形纸片
沿
折叠后,使得点
落在点
的位置,点
恰好落在边
上的点
处.若
,,则
?.
17.
如图所示,圆柱形玻璃杯高为
,底面周长为
,在杯内壁离杯底
的点
处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿
与蜂蜜相对的点
处,则蚂蚁从外壁
处到内壁
处的最短距离为
?
.(杯璧厚度不计)
18.
如图,已知在
中,,,,那么边
上的高等于
?.
三、解答题(共7小题;共60分)
19.
(8分)如图,已知等边三角形
的边长是
.求:
(1)高
的长;
(2)
的面积
.
20.
(8分)如图,四边形
中,,
平分
,,
为
上一点,,,求
的长.
21.
(10分)如图,把一张长方形纸片
折叠起来,使其对角顶点
与
重合,
与
重合,若长方形的长
为
,宽
为
,求:
(1)
的长;
(2)阴影部分
的面积.
22.
(8分)如图,圆柱底面半径为
,高为
,点
,
分别是圆柱两底面圆周上的点,且
,
在同一母线上,用一棉线从
顺着圆柱侧面绕
圈到
,求棉线最短长度.
23.
(8分)一块
的长方形吹塑纸板,按照如图所示的方式设计构图,做新冠疫情防控宣传展板,若在
,
两点之间贴一条彩色胶带,则彩色胶带的长至少是多少米?
24.(8分)
如图,,,
是直线
上的三个点,
于点
,
于点
,且
,,,,求
的长.
25.(10分)
在
中,,,,
是
内部一点,且点
到各边的距离相等,求这个距离.
答案
第一部分
1.
A
【解析】如图所示,
,
为树,且
米,
米,
米.过
作
于
,则
米,
米,
在直角三角形
中,由勾股定理得
米,
故小鸟至少要飞
米.
2.
D
【解析】设
,则
,
在
中,,
即
,
解得
.
3.
A
【解析】在
中,
,,
根据勾股定理得
,
.
故橡皮筋被拉长了
,故选A.
4.
B
【解析】A.
,
以
,,
为边能组成直角三角形,故本选项不符合题意;
B.
,
以
,,
为边不能组成直角三角形,故本选项符合题意;
C.
,
以
,,
为边能组成直角三角形,故本选项不符合题意;
D.
,
以
,,
为边能组成直角三角形,故本选项不符合题意.
故选B.
5.
D
【解析】
是
中点,,
,
折叠,
,
,
在
中,,
,
,
.
6.
A
【解析】设
,由折叠可得
,
是
的中点,
,
在
中,,
解得
,即
.
7.
B
【解析】A.,不能构成直角三角形;
B.,能构成直角三角形;
C.,不能构成直角三角形;
D.,不能构成直角三角形.故选B.
8.
C
【解析】将长方体展开,连接
,
长方体的底面边长分别为
和
,高为
,点
在边
上,且
,
,,根据两点之间线段最短,.
9.
A
【解析】,,
,,
,
即这两点之间的距离是
.故选A.
10.
A
11.
B
【解析】①当吸管放进包装盒且垂直于包装盒底面时露在盒外的长度最长,最长为
.
②
露出部分最短时,包装盒内的吸管与底面对角线和高正好组成直角三角形,
底面对角线长为
,高为
.设包装盒里吸管长为
,
则
,
所以
,
所以露在包装盒外的吸管的长度最短为
.
则吸管露在盒外的部分
的取值范围为
.故选B.
12.
A
【解析】如图,过点
作
于点
,
根据题意,得
米,
米,
在
中,由勾股定理,得
,
,
米,
米.
此时木马上升的高度为
米,故选A.
第二部分
13.
确定,数量
14.
15.
16.
17.
【解析】如图所示,圆柱形玻璃杯的侧面展开图的一半为
,作点
关于
的对称点
,连接
,过点
作
,垂足为点
,
根据题意得
,,
所以
,.
因为
,
所以
,
即从外壁
处到内壁
处的最短距离为
.
18.
【解析】如图,作
,交
边的延长线于
点,
设
,,
在直角
中,,
在直角
中,,
,即
,
由①②得
,,即
,
为
边上的高,
边上的高等于
.
第三部分
19.
(1)
??????(2)
20.
,,,
,
,
.
,
.
平分
,
.
21.
(1)
设
,则
,
在
中,,
,
解得
,
.
??????(2)
过
点作
于
,
则
,
,,,
,
.
22.
圆柱体的展开图如图所示,
用一棉线从
顺着圆柱侧面绕
圈到
的运动最短路线是:,即在圆柱体的展开图长方形中,将长方形平均分成
个小长方形,
沿着
个小长方形的对角线运动到
的路线最短.
圆柱底面半径为
,
长方形的宽即是圆柱体的底面圆的周长为
.
又圆柱高为
,
小长方体的一条边长是
.
根据勾股定理求得
.
.
故棉线的最短长度为
.
23.
过点
作
于
,如图,
从图中可以看出
,
,
在直角
中,
为斜边,
则
.
答:彩色胶带的长至少是
.
24.
设
,则
,
于点
,
于点
,
和
都是直角三角形,
在
中,,
在
中,,
,
,
即
,
解得
,
即
的长为
.
25.
设点
到
各边距离都为
.
因为
,,,
,
所以
是直角三角形.
所以
.
因为
,
所以
.解得
.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
