鲁教版(五四制)数学八年级上册第五章平行四边形5.3 三角形的中位线(1) 导学案无答案
文档属性
| 名称 | 鲁教版(五四制)数学八年级上册第五章平行四边形5.3 三角形的中位线(1) 导学案无答案 |

|
|
| 格式 | doc | ||
| 文件大小 | 50.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-03 12:09:01 | ||
图片预览

文档简介
5.3
三角形的中位线
【学习目标】
1.经历探索、发现、猜想、证明的中位线定理,进一步发展推理论证能力。
2.掌握三角形中位线定理,并能运用其解决实际问题。
3.体会三角形中位线定理的证明过程中所运用的归纳、概括以及转化等数学思想方法。
预习案
复习回顾
平行四边形的性质:
平行四边形的判定:
【自主学习】
中位线的定义
______________________________________________
叫做三角形的中位线,一个三角形有_________
条中位线.
2.
在练习本上画出一个三角形,并画出它的一条中位线.
探究案
探究与思考
三角形的中位线有什么性质?
如图,EF是△ABC
的一条中位线.
(1)量一量DE,BC
的长是多少?你能作出什么猜测?
(2)观察图形中的EF与BC,猜测DE
与BC
位置关系吗?
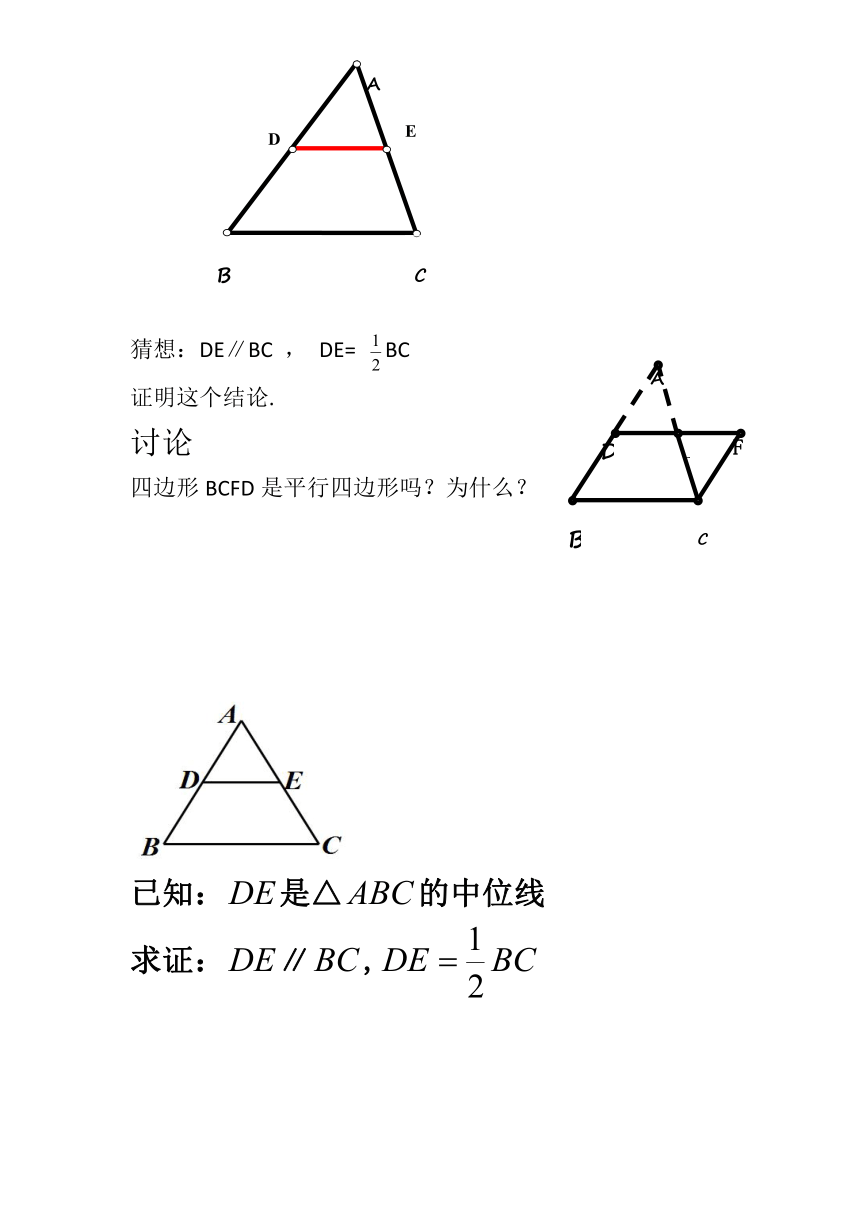
猜想:DE∥BC
,
DE=
BC
证明这个结论.
讨论
四边形BCFD是平行四边形吗?为什么?
已知:是△的中位线
求证:∥,
结论:中位线定理_____________________________________
符号语言
∵DE是△ABC的中位线
——————————————————
——————————————————
知识总结:
1.
定义:连接三角形两边中点的线段叫做三角形的中位线.
2.
三角形的中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.
数学思想:转化思想
1.
把四边形的问题转化为三角形问题解决.
2.
线段的倍分问题可转化为相等问题来解决
数学方法:在三角形的中位线定理的发现过程用到画图、测量、猜想、验证、证明等数学方法.
训练案
课堂检测
1.
如图,MN
为△ABC
的中位线,若∠ABC
=61°,则∠AMN=
,若MN
=12
,则BC
=
.
2.
如图,
△ABC
中,
D
,E
分别为AB,AC
的中点,当BC
=10㎝时,则DE
=
.
3.
如图,已知△ABC中,AB
=
3㎝,BC=3.4㎝,AC=4㎝且D,E,F分别为
AB,BC,AC边的中点,则△DEF的周长是
㎝.
4.如图,四边形ABCD中,AB=AD,E,F,G分别是AC,BC,CD的中点。
求证:∠1=∠2。
C
A
B
D
E
D
E
B
C
A
F
A
D
B
C
E
A
M
B
C
N
A
B
C
D
E
F
A
F
E
D
C
B
G
三角形的中位线
【学习目标】
1.经历探索、发现、猜想、证明的中位线定理,进一步发展推理论证能力。
2.掌握三角形中位线定理,并能运用其解决实际问题。
3.体会三角形中位线定理的证明过程中所运用的归纳、概括以及转化等数学思想方法。
预习案
复习回顾
平行四边形的性质:
平行四边形的判定:
【自主学习】
中位线的定义
______________________________________________
叫做三角形的中位线,一个三角形有_________
条中位线.
2.
在练习本上画出一个三角形,并画出它的一条中位线.
探究案
探究与思考
三角形的中位线有什么性质?
如图,EF是△ABC
的一条中位线.
(1)量一量DE,BC
的长是多少?你能作出什么猜测?
(2)观察图形中的EF与BC,猜测DE
与BC
位置关系吗?
猜想:DE∥BC
,
DE=
BC
证明这个结论.
讨论
四边形BCFD是平行四边形吗?为什么?
已知:是△的中位线
求证:∥,
结论:中位线定理_____________________________________
符号语言
∵DE是△ABC的中位线
——————————————————
——————————————————
知识总结:
1.
定义:连接三角形两边中点的线段叫做三角形的中位线.
2.
三角形的中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.
数学思想:转化思想
1.
把四边形的问题转化为三角形问题解决.
2.
线段的倍分问题可转化为相等问题来解决
数学方法:在三角形的中位线定理的发现过程用到画图、测量、猜想、验证、证明等数学方法.
训练案
课堂检测
1.
如图,MN
为△ABC
的中位线,若∠ABC
=61°,则∠AMN=
,若MN
=12
,则BC
=
.
2.
如图,
△ABC
中,
D
,E
分别为AB,AC
的中点,当BC
=10㎝时,则DE
=
.
3.
如图,已知△ABC中,AB
=
3㎝,BC=3.4㎝,AC=4㎝且D,E,F分别为
AB,BC,AC边的中点,则△DEF的周长是
㎝.
4.如图,四边形ABCD中,AB=AD,E,F,G分别是AC,BC,CD的中点。
求证:∠1=∠2。
C
A
B
D
E
D
E
B
C
A
F
A
D
B
C
E
A
M
B
C
N
A
B
C
D
E
F
A
F
E
D
C
B
G
