鲁教版八年级数学上册 5.4 多边形的内角和与外角和 学案无答案
文档属性
| 名称 | 鲁教版八年级数学上册 5.4 多边形的内角和与外角和 学案无答案 | 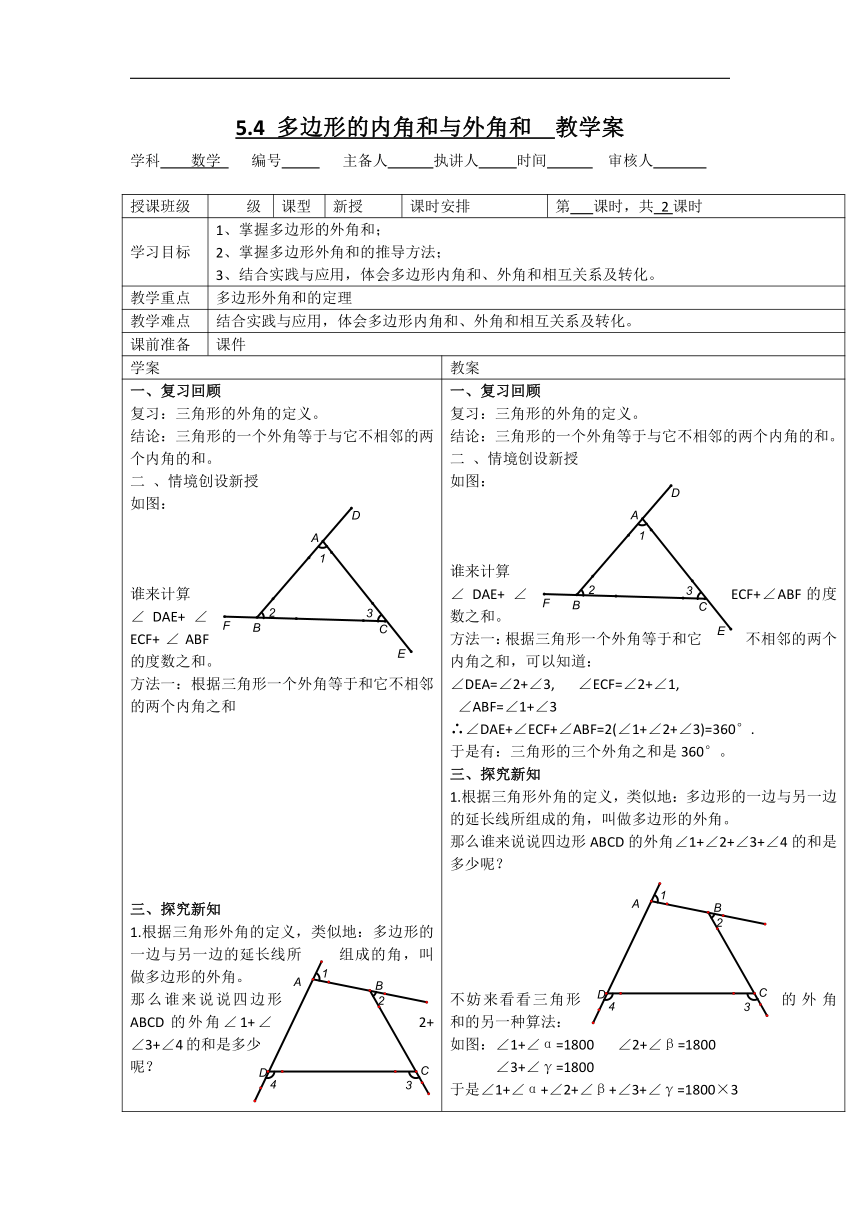 | |
| 格式 | doc | ||
| 文件大小 | 112.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-03 12:10:42 | ||
图片预览

文档简介
5.4
多边形的内角和与外角和
教学案
学科
数学
编号
主备人
执讲人
时间
审核人
授课班级
级
课型
新授
课时安排
第
课时,共
2课时
学习目标
1、掌握多边形的外角和;2、掌握多边形外角和的推导方法;3、结合实践与应用,体会多边形内角和、外角和相互关系及转化。
教学重点
多边形外角和的定理
教学难点
结合实践与应用,体会多边形内角和、外角和相互关系及转化。
课前准备
课件
学案
教案
一、复习回顾复习:三角形的外角的定义。结论:三角形的一个外角等于与它不相邻的两个内角的和。二
、情境创设新授如图:谁来计算∠DAE+∠ECF+∠ABF的度数之和。方法一:根据三角形一个外角等于和它不相邻的两个内角之和三、探究新知1.根据三角形外角的定义,类似地:多边形的一边与另一边的延长线所组成的角,叫做多边形的外角。那么谁来说说四边形ABCD的外角∠1+∠2+∠3+∠4的和是多少呢?三角形的外角和的另一种算法:2、引申为:n边形:3、结论:四、例题讲解解答题:1、一个多边形的内角和是外角和的3倍,求这个多边形的边数。2、一个多边形的每一个外角都是60°,求这个多边形的内角和。3、一个多边形所有内角与它的一个外角的和等于2000°,求这个外角的度数。注重方程思想的渗透和分析问题解决问题的能力训练。五、课堂练习课本随堂练习六、课堂收获七、布置作业课本习题
一、复习回顾复习:三角形的外角的定义。结论:三角形的一个外角等于与它不相邻的两个内角的和。二
、情境创设新授如图:谁来计算∠DAE+∠ECF+∠ABF的度数之和。方法一:根据三角形一个外角等于和它不相邻的两个内角之和,可以知道:∠DEA=∠2+∠3,
∠ECF=∠2+∠1,
∠ABF=∠1+∠3∴∠DAE+∠ECF+∠ABF=2(∠1+∠2+∠3)=360°.于是有:三角形的三个外角之和是360°。三、探究新知1.根据三角形外角的定义,类似地:多边形的一边与另一边的延长线所组成的角,叫做多边形的外角。那么谁来说说四边形ABCD的外角∠1+∠2+∠3+∠4的和是多少呢?不妨来看看三角形的外角和的另一种算法:如图:∠1+∠α=1800
∠2+∠β=1800
∠3+∠γ=1800于是∠1+∠α+∠2+∠β+∠3+∠γ=1800×3又∠1+∠2+∠3=1800,∴∠α+∠β+∠γ=360°.2.同样,类似地有:学生板演,得出四边形的外角和为360°.引申为:n边形中,每个内角与相邻的外角都是互补关系,共有n组,于是内外角总和为n×180°,其内角和为(n-2)×180°,那么外角和为360°.3.得出结论:任意多边形的外角和为360°.四、例题讲解解答题:1、一个多边形的内角和是外角和的3倍,求这个多边形的边数。2、一个多边形的每一个外角都是60°,求这个多边形的内角和。3、一个多边形所有内角与它的一个外角的和等于2000°,求这个外角的度数。注重方程思想的渗透和分析问题解决问题的能力训练。五、课堂练习课本随堂练习六、课堂小结1).外角和的推导过程2).外角和定理的应用3).猜想:多边形的外角中,最多能有几个角是钝角?七、布置作业课本习题
知识梳理
5.4
多边形的内角和与外角和(2)任意多边形的外角和为360°
收获反思
通过本节课的学习,学生掌握多边形的外角和;掌握多边形外角和的推导方法;能结合实践与应用,体会多边形内角和、外角和相互关系及转化。
多边形的内角和与外角和
教学案
学科
数学
编号
主备人
执讲人
时间
审核人
授课班级
级
课型
新授
课时安排
第
课时,共
2课时
学习目标
1、掌握多边形的外角和;2、掌握多边形外角和的推导方法;3、结合实践与应用,体会多边形内角和、外角和相互关系及转化。
教学重点
多边形外角和的定理
教学难点
结合实践与应用,体会多边形内角和、外角和相互关系及转化。
课前准备
课件
学案
教案
一、复习回顾复习:三角形的外角的定义。结论:三角形的一个外角等于与它不相邻的两个内角的和。二
、情境创设新授如图:谁来计算∠DAE+∠ECF+∠ABF的度数之和。方法一:根据三角形一个外角等于和它不相邻的两个内角之和三、探究新知1.根据三角形外角的定义,类似地:多边形的一边与另一边的延长线所组成的角,叫做多边形的外角。那么谁来说说四边形ABCD的外角∠1+∠2+∠3+∠4的和是多少呢?三角形的外角和的另一种算法:2、引申为:n边形:3、结论:四、例题讲解解答题:1、一个多边形的内角和是外角和的3倍,求这个多边形的边数。2、一个多边形的每一个外角都是60°,求这个多边形的内角和。3、一个多边形所有内角与它的一个外角的和等于2000°,求这个外角的度数。注重方程思想的渗透和分析问题解决问题的能力训练。五、课堂练习课本随堂练习六、课堂收获七、布置作业课本习题
一、复习回顾复习:三角形的外角的定义。结论:三角形的一个外角等于与它不相邻的两个内角的和。二
、情境创设新授如图:谁来计算∠DAE+∠ECF+∠ABF的度数之和。方法一:根据三角形一个外角等于和它不相邻的两个内角之和,可以知道:∠DEA=∠2+∠3,
∠ECF=∠2+∠1,
∠ABF=∠1+∠3∴∠DAE+∠ECF+∠ABF=2(∠1+∠2+∠3)=360°.于是有:三角形的三个外角之和是360°。三、探究新知1.根据三角形外角的定义,类似地:多边形的一边与另一边的延长线所组成的角,叫做多边形的外角。那么谁来说说四边形ABCD的外角∠1+∠2+∠3+∠4的和是多少呢?不妨来看看三角形的外角和的另一种算法:如图:∠1+∠α=1800
∠2+∠β=1800
∠3+∠γ=1800于是∠1+∠α+∠2+∠β+∠3+∠γ=1800×3又∠1+∠2+∠3=1800,∴∠α+∠β+∠γ=360°.2.同样,类似地有:学生板演,得出四边形的外角和为360°.引申为:n边形中,每个内角与相邻的外角都是互补关系,共有n组,于是内外角总和为n×180°,其内角和为(n-2)×180°,那么外角和为360°.3.得出结论:任意多边形的外角和为360°.四、例题讲解解答题:1、一个多边形的内角和是外角和的3倍,求这个多边形的边数。2、一个多边形的每一个外角都是60°,求这个多边形的内角和。3、一个多边形所有内角与它的一个外角的和等于2000°,求这个外角的度数。注重方程思想的渗透和分析问题解决问题的能力训练。五、课堂练习课本随堂练习六、课堂小结1).外角和的推导过程2).外角和定理的应用3).猜想:多边形的外角中,最多能有几个角是钝角?七、布置作业课本习题
知识梳理
5.4
多边形的内角和与外角和(2)任意多边形的外角和为360°
收获反思
通过本节课的学习,学生掌握多边形的外角和;掌握多边形外角和的推导方法;能结合实践与应用,体会多边形内角和、外角和相互关系及转化。
