18.4焦耳定律 2021-2022学年人教版九年级物理全一册(含答案)
文档属性
| 名称 | 18.4焦耳定律 2021-2022学年人教版九年级物理全一册(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 910.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-09-04 11:19:12 | ||
图片预览


文档简介
2021人教版九年级物理18.4焦耳定律考点
考点一.焦耳定律应用
1.如图所示,给电炉通电后,电炉丝热得发红,而用手触摸与之连接的导线却不觉得烫手,这是因为( )
A.电流通过导线时没有产生热效应
B.通过电炉丝的电流比通过导线的电流大得多
C.电炉丝的电阻比导线的电阻小得多
D.电炉丝消耗的电功率比导线消耗的电功率大得多
2.将口香糖的锡箔纸包装剥下来,用小刀剪成约5mm宽、10cm长的细条,做成两头宽、中间窄的纺锤形状(如图所示)。再把锡箔纸两头有亮光的一面(锡箔),分别用手摁在干电池的正负极上,3秒钟左右,锡箔纸中间狭窄部分即开始燃烧起来。关于此情景下列说法中正确的是( )
A.锡箔燃烧是因为此处电流较大
B.相同长度锡箔较窄处的电阻较小
C.锡箔中电子从电池正极流向负极
D.相同长度锡箔较窄处的电压较大
3.小明发现当给家中的电灯通电后,灯丝热得发光,而与灯泡串联的导线温度几乎感觉不到变化,对这一现象的解释,正确的是( )
A.通过灯丝的电流大些
B.电流在导线中不发生热效应
C.制成灯丝的材料电阻较小
D.导线和灯丝中的电流相同,但灯丝电阻更大
考点二.探究电流通过导体时产生的热量与什么因素有关
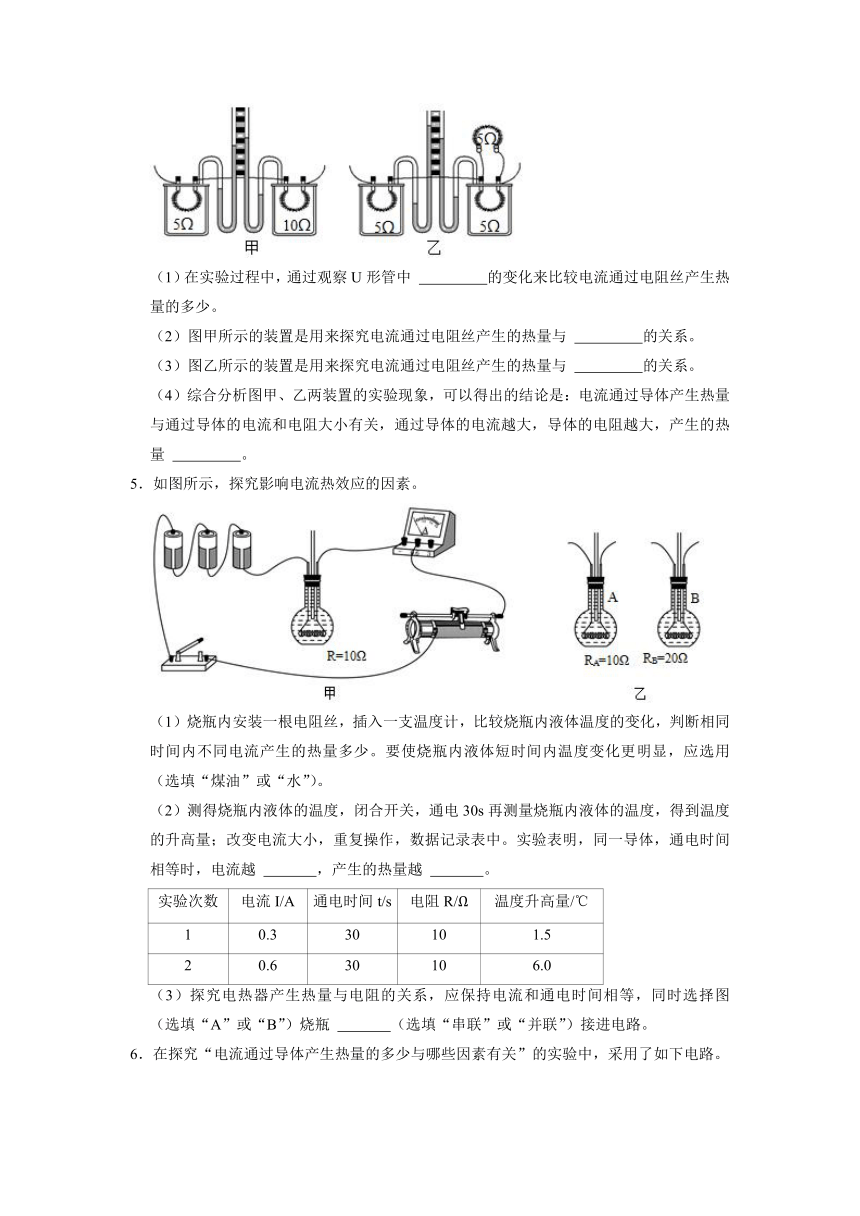
4.在做“探究电流通过导体时产生的热量与什么因素有关”的实验时,小龙采用了如图所示的实验装置。(两个透明容器中封闭着等量气体)
(1)在实验过程中,通过观察U形管中
的变化来比较电流通过电阻丝产生热量的多少。
(2)图甲所示的装置是用来探究电流通过电阻丝产生的热量与
的关系。
(3)图乙所示的装置是用来探究电流通过电阻丝产生的热量与
的关系。
(4)综合分析图甲、乙两装置的实验现象,可以得出的结论是:电流通过导体产生热量与通过导体的电流和电阻大小有关,通过导体的电流越大,导体的电阻越大,产生的热量
。
5.如图所示,探究影响电流热效应的因素。
(1)烧瓶内安装一根电阻丝,插入一支温度计,比较烧瓶内液体温度的变化,判断相同时间内不同电流产生的热量多少。要使烧瓶内液体短时间内温度变化更明显,应选用
(选填“煤油”或“水”)。
(2)测得烧瓶内液体的温度,闭合开关,通电30s再测量烧瓶内液体的温度,得到温度的升高量;改变电流大小,重复操作,数据记录表中。实验表明,同一导体,通电时间相等时,电流越
,产生的热量越
。
实验次数
电流I/A
通电时间t/s
电阻R/Ω
温度升高量/℃
1
0.3
30
10
1.5
2
0.6
30
10
6.0
(3)探究电热器产生热量与电阻的关系,应保持电流和通电时间相等,同时选择图
(选填“A”或“B”)烧瓶
(选填“串联”或“并联”)接进电路。
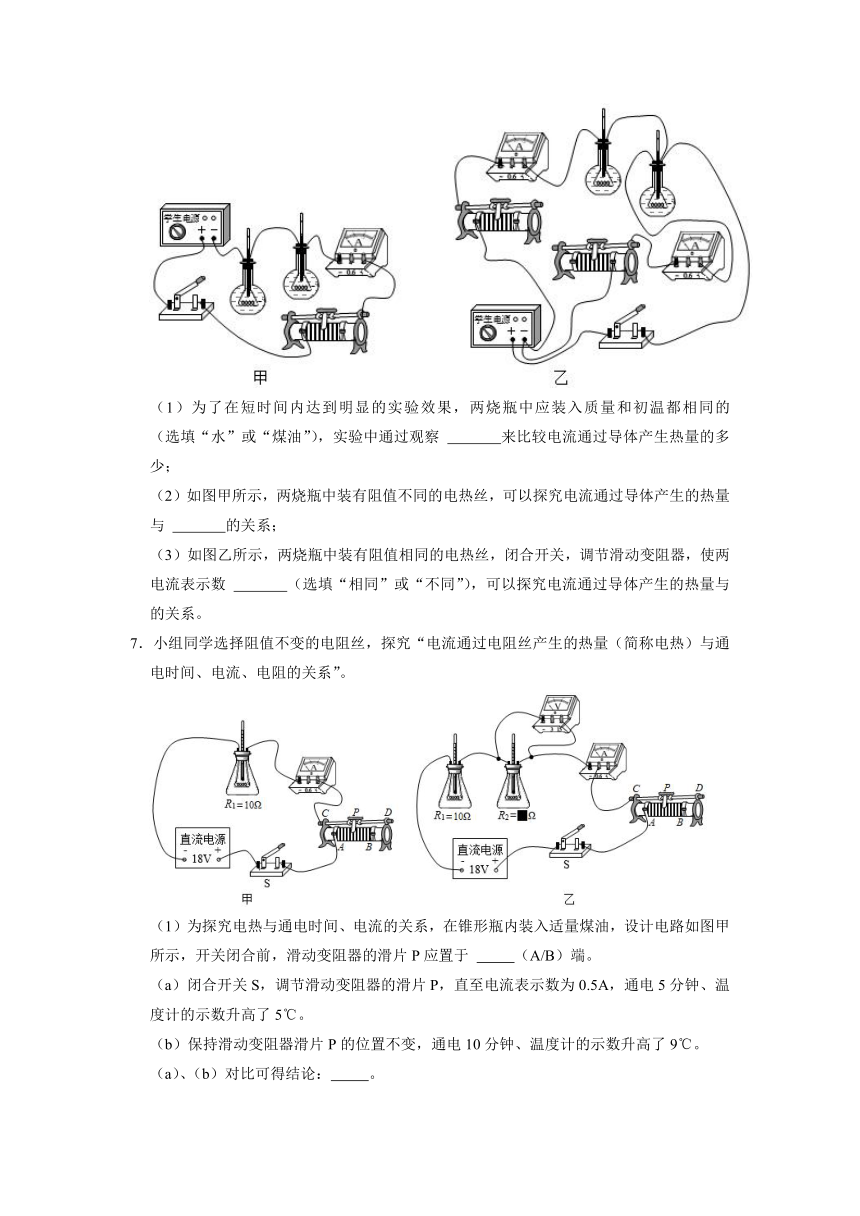
6.在探究“电流通过导体产生热量的多少与哪些因素有关”的实验中,采用了如下电路。
(1)为了在短时间内达到明显的实验效果,两烧瓶中应装入质量和初温都相同的
(选填“水”或“煤油”),实验中通过观察
来比较电流通过导体产生热量的多少;
(2)如图甲所示,两烧瓶中装有阻值不同的电热丝,可以探究电流通过导体产生的热量与
的关系;
(3)如图乙所示,两烧瓶中装有阻值相同的电热丝,闭合开关,调节滑动变阻器,使两电流表示数
(选填“相同”或“不同”),可以探究电流通过导体产生的热量与
的关系。
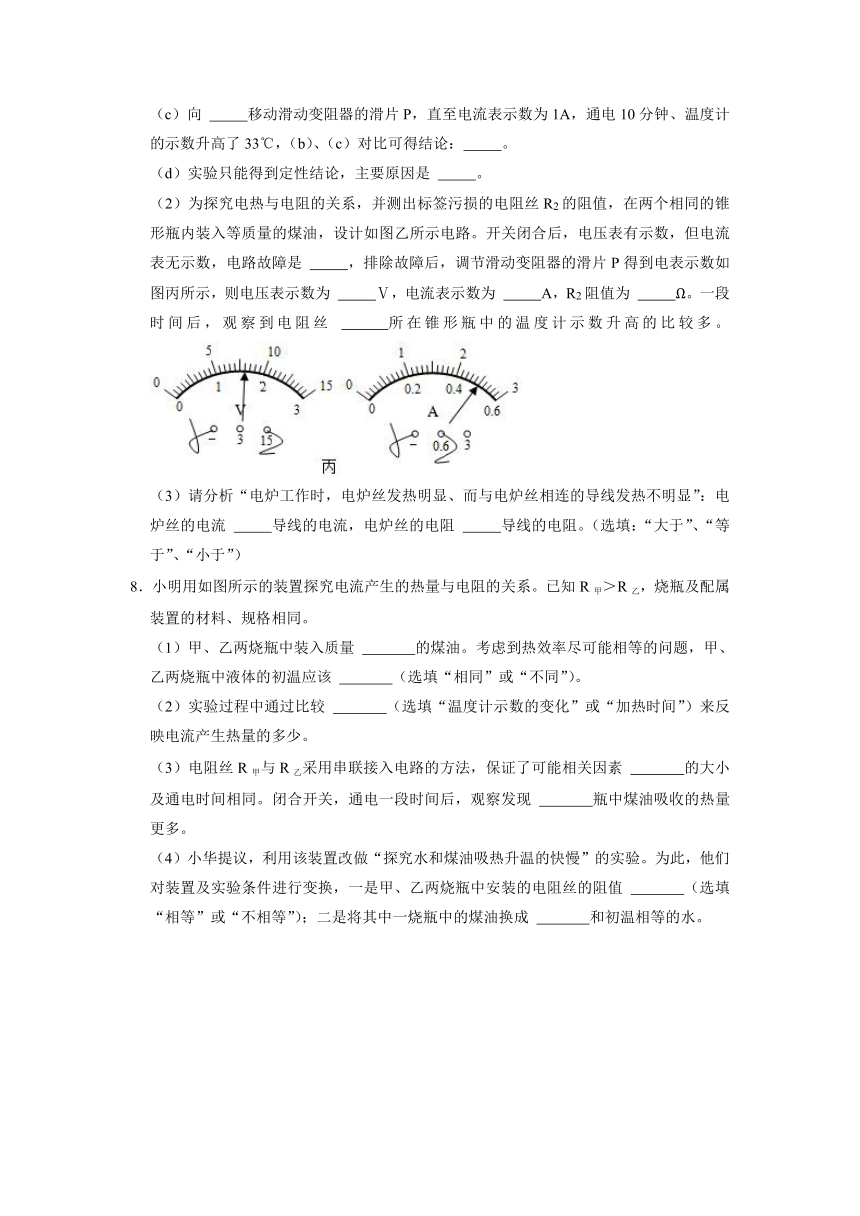
7.小组同学选择阻值不变的电阻丝,探究“电流通过电阻丝产生的热量(简称电热)与通电时间、电流、电阻的关系”。
(1)为探究电热与通电时间、电流的关系,在锥形瓶内装入适量煤油,设计电路如图甲所示,开关闭合前,滑动变阻器的滑片P应置于
(A/B)端。
(a)闭合开关S,调节滑动变阻器的滑片P,直至电流表示数为0.5A,通电5分钟、温度计的示数升高了5℃。
(b)保持滑动变阻器滑片P的位置不变,通电10分钟、温度计的示数升高了9℃。
(a)、(b)对比可得结论:
。
(c)向
移动滑动变阻器的滑片P,直至电流表示数为1A,通电10分钟、温度计的示数升高了33℃,(b)、(c)对比可得结论:
。
(d)实验只能得到定性结论,主要原因是
。
(2)为探究电热与电阻的关系,并测出标签污损的电阻丝R2的阻值,在两个相同的锥形瓶内装入等质量的煤油,设计如图乙所示电路。开关闭合后,电压表有示数,但电流表无示数,电路故障是
,排除故障后,调节滑动变阻器的滑片P得到电表示数如图丙所示,则电压表示数为
Ⅴ,电流表示数为
A,R2阻值为
Ω。一段时间后,观察到电阻丝
所在锥形瓶中的温度计示数升高的比较多。
(3)请分析“电炉工作时,电炉丝发热明显、而与电炉丝相连的导线发热不明显”:电炉丝的电流
导线的电流,电炉丝的电阻
导线的电阻。(选填:“大于”、“等于”、“小于”)
8.小明用如图所示的装置探究电流产生的热量与电阻的关系。已知R甲>R乙,烧瓶及配属装置的材料、规格相同。
(1)甲、乙两烧瓶中装入质量
的煤油。考虑到热效率尽可能相等的问题,甲、乙两烧瓶中液体的初温应该
(选填“相同”或“不同”)。
(2)实验过程中通过比较
(选填“温度计示数的变化”或“加热时间”)来反映电流产生热量的多少。
(3)电阻丝R甲与R乙采用串联接入电路的方法,保证了可能相关因素
的大小及通电时间相同。闭合开关,通电一段时间后,观察发现
瓶中煤油吸收的热量更多。
(4)小华提议,利用该装置改做“探究水和煤油吸热升温的快慢”的实验。为此,他们对装置及实验条件进行变换,一是甲、乙两烧瓶中安装的电阻丝的阻值
(选填“相等”或“不相等”);二是将其中一烧瓶中的煤油换成
和初温相等的水。
9.如图所示是某实验小组探究“电流产生的热量与哪些因素有关”的实验装置。
(1)实验时,两瓶煤油的质量要
,在这个实验中,电流产生的热量的多少,是通过
体现出来。为了便于实验观察,还应使两瓶煤油的
相同。
(2)图甲中,RA与RB采用串联的方式,其目的是为了控制通电时间、
相等,选用的RA和RB的阻值大小
(选填“相等”或“不相等”),实验中选用煤油而不选用水,主要是因为水的
比煤油大。
(3)图甲探究的是电热与
的关系。按图乙方法进行实验时,观察到在相同的时间内C瓶煤油比D瓶煤油的温度上升更多,这说明:其他条件相同时,
越大,电流通过导体产生的热量越多。
10.在“探究电流产生的热量与哪些因素有关”的实验中,实验电路如图1所示,其中R1>R2。
实验一:探究电流产生的热量与电阻大小的关系:
(1)请按照图1中的电路图将图2实物图连接完整;
(2)实验电路按照图1中的电路图连接是为了控制通电时间相同和控制
;电阻丝放出热量的多少,通过
来进行判断。
(3)为了便于比较两根电阻丝通过电流后产生热量的多少,a、b两瓶中要装入
相等、初温相同的同种液体。为了在较短时间内达到明显的实验效果,实验时选用煤油而不选水,是因为煤油的比热容
水的比热容(选填“大于”、“等于”或“小于”)。
实验二:探究电流产生的热量与电流大小的关系:
(4)闭合开关,移动滑动变阻器的滑片,使电路中的电流变成实验一中电流的2倍,且通电时间相同。实验发现:用电阻丝R1加热的煤油,在实验一中温度升高△t1,在实验二中温度升高△t1′,则△t1′
2△t1(选填“大于”、“等于”或“小于”),该实验说明电流产生的热量与电流大小
正比例关系(选填“成”或“不成”)。实验中,用电阻丝R2加热煤油重复以上实验步骤,也可以得出相同的结论。
(5)如果在两烧瓶中分别装入质量相等的不同液体,并接入两根阻值
的电阻丝(选填“相同”或“不同”),就可用这个装置来探究两种不同液体的吸热性质。假设a烧瓶中液体的质量为m,瓶中电阻丝的阻值为R,测出通过它的电流为I,通电一段时间t后,温度计的示数变化量为△t,若不计热量损失,则a液体的比热容为
(用所给出的物理量写出比热容的表达式)。
考点三.电热综合计算
11.如图甲所示是小媛家新买的新型电热水壶,该电热水壶有加热、保温和干烧断电功能,其简化电路如图乙所示。S1是壶底温控开关,通常闭合,当壶底发热盘温度达到120℃自动断开,S2是壶壁温控开关,闭合时对水加热,断开时对水保温。已知电热水壶加热功率为1100W,保温功率为55W。求:
(1)电热水壶处于加热状态时,电路中的电流;
(2)电阻R2的阻值;
(3)若水烧开后,S2没有自动断开,当壶里的水烧干瞬间,发热盘的温度为110℃,已知发热盘质量为0.44kg,比热容为0.5×103J/(kg?℃),若水壶的加热效率为80%,则经过多长时间S1才会断开?
12.智能全自动茶炉(如图)内有加热电阻,集抽水、烧水、保温于一体,美观大方,容易操作,如表为某款智能全自动茶炉的部分参数。[ρ水=1.0×103kg/m3,c水=4.2×103J/(kg?℃)]求:
产品名称
智能全自动茶炉
产品型号
XXXX
烧水功率
1210W
容量
0.8L
保温功率
22W
额定电压
220V
(1)将一壶水从20℃加热到70℃,水吸收的热量。
(2)保温状态下通过茶炉的电流。
(3)若用电高峰时,家庭电路的实际电压仅为200V,求该茶炉的实际加热功率(加热电阻阻值不变)。
13.如图所示是某电热器装置的简化电路图,开关S可切换加热和保温两种状态,它的额定电压为220V,额定加热功率是P热=1100W,R1、R2是发热电阻,R2=440Ω。已知电路电压正常,已知水的比热容为4.2×103J/(kg?℃),试完成下列问题:
(1)图中电阻R1的阻值是多大?
(2)该电热器的保温功率P温是多大?
(3)若该电热器将2kg的水从20℃,加热到75℃,需要8min时间,则它加热时将电能转化为水的内能的效率为多少?
14.多功能养生壶具有精细烹饪、营养量化等功能,深受市场认可和欢迎,如图乙所示是某品牌养生壶简化电路图。
[ρ水=1×103kg/m3,c水=4.2×103J/(kg?℃)]
中温挡功率/W
550
高温挡功率/W
1100
容积/L
1
(1)求R1的阻值。
(2)养生壶在低温挡工作时,求电路中的电流大小。
(3)在标准大气压下,使用高温挡将初温是12℃的一壶水烧开,若养生壶高温挡加热效率为80%,求烧开一壶水需要的时间。
15.如图是小灵家新购买的电热水器的简化原理图,R1和R2为定值电阻,S为温控开关,a、b是开关的连接触点,电热水器部分参数如表所示。求:
额定电压
220V
加热功率
2000W
保温功率
200W
(1)当把25kg的水由20℃加热到60℃时,水吸收的热量;若热水器加热时的效率为80%,需要消耗的电能。[c水=4.2×103J/(kg?℃)]
(2)R2的阻值。
考点四.比值计算
16.甲、乙两个电热器的电阻之比为2:3,通电相同时间产生的热量之比为6:1,则通过甲、乙的电流之比为( )
A.3:1
B.1:3
C.3:2
D.2:3
17.甲乙两电热器通过的电流之比为3:2,通电时间之比为2:3,电阻之比为4:3,则产生热量之比为( )
A.1:2
B.2:9
C.2:1
D.9:2
18.一阻值为R的电阻丝接在电压为U的电路中,在t时间内放出的热量为Q,现把该电阻丝对折起来接到原来的电路中,放出同样多的热量,需要的时间是( )
A.
B.
C.t
D.2t
19.甲、乙两段导体通电时间相同,甲的电阻是乙的3倍,甲、乙产生的热量之比是4:3,则通过甲、乙两导体的电流之比是( )
A.2:3
B.2:1
C.9:2
D.3:2
20.某一阻值为R的电阻,通过的电流为I时,在t时间内产生的热量是Q。则当另一阻值为2R的电阻,通过电流是2I时,在同样的t时间内产生的热量为( )
A.2Q
B.4Q
C.8Q
D.16Q
2021人教版九年级物理18.4焦耳定律考点
参考答案
1.如图所示,给电炉通电后,电炉丝热得发红,而用手触摸与之连接的导线却不觉得烫手,这是因为( )
A.电流通过导线时没有产生热效应
B.通过电炉丝的电流比通过导线的电流大得多
C.电炉丝的电阻比导线的电阻小得多
D.电炉丝消耗的电功率比导线消耗的电功率大得多
【解答】解:A、由于导线有电阻,电流通过导线时,导线会发热,产生热效应,故A错误;
BCD、电炉在使用时,电炉丝和导线串联,通过它们的电流相等,通电时间t相同,由于R电炉丝>R导线,根据Q=I2Rt可知,电流产生的热量:Q电炉丝>Q导线,根据P=I2R知,导线消耗的电功率比电炉丝消耗的电功率小,因而出现电炉丝热得发红,而与电炉丝相连的导线却不怎么发热的现象;故BC错误,D正确。
故选:D。
2.将口香糖的锡箔纸包装剥下来,用小刀剪成约5mm宽、10cm长的细条,做成两头宽、中间窄的纺锤形状(如图所示)。再把锡箔纸两头有亮光的一面(锡箔),分别用手摁在干电池的正负极上,3秒钟左右,锡箔纸中间狭窄部分即开始燃烧起来。关于此情景下列说法中正确的是( )
A.锡箔燃烧是因为此处电流较大
B.相同长度锡箔较窄处的电阻较小
C.锡箔中电子从电池正极流向负极
D.相同长度锡箔较窄处的电压较大
【解答】解:
A、由图可知,锡箔纸中间燃烧部分与两头是串联的,由串联电路的电流特点可知燃烧部分与两头的电流相等,故A错误;
B、长度和材料相同时,较窄处横截面积较小,其电阻较大,故B错误;
C、在电源外部,电流从电源正极流出经锡箔纸回到电源负极;而电子定向移动的方向与电流方向相反,所以电子从负极经锡箔纸流向正极,故C错误;
D、由B选项知,较窄处电阻较大,电流相等,由U=IR可知,较窄处的电压较大,故D正确。
故选:D。
3.小明发现当给家中的电灯通电后,灯丝热得发光,而与灯泡串联的导线温度几乎感觉不到变化,对这一现象的解释,正确的是( )
A.通过灯丝的电流大些
B.电流在导线中不发生热效应
C.制成灯丝的材料电阻较小
D.导线和灯丝中的电流相同,但灯丝电阻更大
【解答】解:因为灯丝和导线串联,所以通过灯丝和导线的电流、通电时间都相同,根据焦耳定律Q=I2Rt,灯丝电阻大,产生热量多,而导线电阻非常小,产生的热量就很小,所以电灯通电后,灯丝热得发光,而与灯泡串联的导线温度几乎感觉不到变化。故选项A、B、C都不正确,D选项正确。
故选:D。
4.在做“探究电流通过导体时产生的热量与什么因素有关”的实验时,小龙采用了如图所示的实验装置。(两个透明容器中封闭着等量气体)
(1)在实验过程中,通过观察U形管中
液面高度 的变化来比较电流通过电阻丝产生热量的多少。
(2)图甲所示的装置是用来探究电流通过电阻丝产生的热量与
电阻 的关系。
(3)图乙所示的装置是用来探究电流通过电阻丝产生的热量与
电流 的关系。
(4)综合分析图甲、乙两装置的实验现象,可以得出的结论是:电流通过导体产生热量与通过导体的电流和电阻大小有关,通过导体的电流越大,导体的电阻越大,产生的热量
越多 。
【解答】解:(1)电流通过导体产生热量的多少不能直接观察,可以利用转换法,在实验过程中,通过观察U形管中液面高度的变化来比较电流通过电阻丝产生热量的多少;
(2)如图甲,两个电阻串联在电路中,通过的电流相同,通电时间相同,电阻不同,由控制变量法的要求可知,图甲是探究电流产生热量跟电阻大小的关系;
(3)图乙装置中是两个5Ω的电阻并联之后再与一个5Ω的电阻串联,根据串并联电路的电流特点可知,右端两个电阻的总电流和左端的电阻通过的电流相等,则左端容器中电阻通过的电流大于右端容器中电阻通过的电流,由于两个容器内的电阻阻值相同,通电时间相同,而电流不同,由控制变量法的要求可知,图乙是探究电流产生热量跟电流的关系;
(4)综合分析图甲和图乙两装置的实验现象,可以得出的结论:电流通过导体产生的热量与通过导体的电流和电阻大小有关,通过导体的电流越大,导体的电阻越大,产生的热量越多。
故答案为:(1)液面高度;(2)电阻;(3)电流;(4)越多。
5.如图所示,探究影响电流热效应的因素。
(1)烧瓶内安装一根电阻丝,插入一支温度计,比较烧瓶内液体温度的变化,判断相同时间内不同电流产生的热量多少。要使烧瓶内液体短时间内温度变化更明显,应选用
煤油 (选填“煤油”或“水”)。
(2)测得烧瓶内液体的温度,闭合开关,通电30s再测量烧瓶内液体的温度,得到温度的升高量;改变电流大小,重复操作,数据记录表中。实验表明,同一导体,通电时间相等时,电流越
大 ,产生的热量越
多 。
实验次数
电流I/A
通电时间t/s
电阻R/Ω
温度升高量/℃
1
0.3
30
10
1.5
2
0.6
30
10
6.0
(3)探究电热器产生热量与电阻的关系,应保持电流和通电时间相等,同时选择图
(选填“A”或“B”)烧瓶
串联 (选填“串联”或“并联”)接进电路。
【解答】解:(1)由于煤油的比热容较小,质量相同吸收热量相同时,温度变化比较明显,应选用煤油进行实验;
(2)由表格中数据知,通电时间和电阻相等,电流增大为原来的2倍,温度升高为原来的4倍,即产生的热量为原来的4倍,可知通电时间和电阻相等,电流越大,产生的热量越多,产生的热量与电流的2次方成正比;
(3)若要探究电热器产生热量与电阻的关系,应保持电流和通电时间相等,电阻不同,所以应该选择B烧瓶和甲图中的烧瓶串联。
故答案为:(1)煤油;(2)大;多;(3)B;串联。
6.在探究“电流通过导体产生热量的多少与哪些因素有关”的实验中,采用了如下电路。
(1)为了在短时间内达到明显的实验效果,两烧瓶中应装入质量和初温都相同的
煤油 (选填“水”或“煤油”),实验中通过观察
两支温度计示数变化 来比较电流通过导体产生热量的多少;
(2)如图甲所示,两烧瓶中装有阻值不同的电热丝,可以探究电流通过导体产生的热量与
电阻 的关系;
(3)如图乙所示,两烧瓶中装有阻值相同的电热丝,闭合开关,调节滑动变阻器,使两电流表示数
不同 (选填“相同”或“不同”),可以探究电流通过导体产生的热量与
电流 的关系。
【解答】解:(1)根据Q吸=cm△t
知,只有两个烧瓶中装入初温度和质量均相同的煤油时,才能通过煤油的温度变化量来反映电流产生热量的多少;
若将烧瓶中装有水,则由Q=cm△t可知:在相同质量的水和煤油中,吸收的相同的热量时,由于水的比热容大,温度升高的度数少,温度计的示数变化不明显,故为了实验效果明显,应选用质量相同的煤油而不用水;
实验中通过观察两支温度计示数变化来比较电流产生的热量的多少,这用到了转换法;
(2)如图甲所示,两电阻串联,通过两电阻的电流和通电时间相同,改变电阻,可以探究电流通过导体产生的热量与电阻的关系;
(3)如图乙所示,两烧瓶中装有阻值相同的电热丝,闭合开关,控制电阻和通电时间相同,通过调节滑动变阻器改变电路的电流,观察同一只烧瓶中煤油升高的温度计的示数变化,可以探究电流通过导体产生的热量与电流的关系。
故答案为:(1)煤油;两支温度计示数变化;(2)电阻;(3)不同;电流。
7.小组同学选择阻值不变的电阻丝,探究“电流通过电阻丝产生的热量(简称电热)与通电时间、电流、电阻的关系”。
(1)为探究电热与通电时间、电流的关系,在锥形瓶内装入适量煤油,设计电路如图甲所示,开关闭合前,滑动变阻器的滑片P应置于
(A/B)端。
(a)闭合开关S,调节滑动变阻器的滑片P,直至电流表示数为0.5A,通电5分钟、温度计的示数升高了5℃。
(b)保持滑动变阻器滑片P的位置不变,通电10分钟、温度计的示数升高了9℃。
(a)、(b)对比可得结论: 在电流大小和电阻大小相同时,通电时间越长,电流通过电阻产生的热量越多 。
(c)向
A端 移动滑动变阻器的滑片P,直至电流表示数为1A,通电10分钟、温度计的示数升高了33℃,(b)、(c)对比可得结论: 在通电时间和电阻大小相同时,电流越大,电流通过电阻产生的热量越多 。
(d)实验只能得到定性结论,主要原因是
实验中只能通过温度计示数的变化量来反映电流通过电阻产生的热量的多少,无法精确测量电阻产生的热量 。
(2)为探究电热与电阻的关系,并测出标签污损的电阻丝R2的阻值,在两个相同的锥形瓶内装入等质量的煤油,设计如图乙所示电路。开关闭合后,电压表有示数,但电流表无示数,电路故障是
R2断路 ,排除故障后,调节滑动变阻器的滑片P得到电表示数如图丙所示,则电压表示数为
8 Ⅴ,电流表示数为
0.5 A,R2阻值为
16 Ω。一段时间后,观察到电阻丝
R2 所在锥形瓶中的温度计示数升高的比较多。
(3)请分析“电炉工作时,电炉丝发热明显、而与电炉丝相连的导线发热不明显”:电炉丝的电流
等于 导线的电流,电炉丝的电阻
大于 导线的电阻。(选填:“大于”、“等于”、“小于”)
【解答】解:(1)滑动变阻器有保护电路的作用,开关闭合前,滑动变阻器的滑片P应置于阻值最大处,故位于B端;
(b)两次实验中,电阻和电流大小均相同,通电时间不同,(b)中温度计升高的示数较大,说明电流通过电阻产生的热量多,可得结论:在电流大小和电阻大小相同时,通电时间越长,电流通过电阻产生的热量越多;
(c)(c)实验中电流表示数变大,根据欧姆定律可知电路中的总电阻变小,滑动变阻器接入电路中的电阻变小,故应向A端移动滑片;
(b)、(c)两次实验中,电阻大小和通电时间均相同,(c)中电流大于(b)中电流,且温度计升高的示数较大,说明电流通过电阻产生的热量多,可得结论:在通电时间和电阻大小相同时,电流越大,电流通过电阻产生的热量越多;
(d)实验只能得到定性结论,主要原因是实验中只能通过温度计示数的变化量来反映电流通过电阻产生的热量的多少,无法精确测量电阻产生的热量;
(2)开关闭合后,电压表有示数,说明电压表与电源接通,但电流表无示数,说明电路中有断路的地方,电路故障是R2断路;
从图乙中可知,闭合开关后,两电阻丝和滑动变阻器串联,电流表测量电路电流,电压表测量R2两端的电压。
电压表选择大量程,分度值为0.5V,示数为8V,电流表选择小量程,分度值为0.02A,示数为0.5A;
根据欧姆定律可知R2的阻值R2===16Ω;
已知R1=10Ω<R2,根据Q=I2Rt可知一段时间后,电阻丝R2产生的热量多,故观察到电阻丝R2所在锥形瓶中的温度计示数升高的比较多;
(3)电炉丝和导线串联,故电炉丝的电流等于导线的电流,电炉丝的电阻大于导线的电阻,根据Q=I2Rt可知通电相同时间,电炉丝产生的热量大于导线产生的热量,故电炉工作时,电炉丝发热明显、而与电炉丝相连的导线发热不明显。
故答案为:(1)B;(b)在电流大小和电阻大小相同时,通电时间越长,电流通过电阻产生的热量越多;(c)A端;在通电时间和电阻大小相同时,电流越大,电流通过电阻产生的热量越多;(d)实验中只能通过温度计示数的变化量来反映电流通过电阻产生的热量的多少,无法精确测量电阻产生的热量;
(2)R2断路;8;0.5;16;R2;(3)等于;大于。
8.小明用如图所示的装置探究电流产生的热量与电阻的关系。已知R甲>R乙,烧瓶及配属装置的材料、规格相同。
(1)甲、乙两烧瓶中装入质量
相同 的煤油。考虑到热效率尽可能相等的问题,甲、乙两烧瓶中液体的初温应该
相同 (选填“相同”或“不同”)。
(2)实验过程中通过比较
温度计示数的变化 (选填“温度计示数的变化”或“加热时间”)来反映电流产生热量的多少。
(3)电阻丝R甲与R乙采用串联接入电路的方法,保证了可能相关因素
电流 的大小及通电时间相同。闭合开关,通电一段时间后,观察发现
甲 瓶中煤油吸收的热量更多。
(4)小华提议,利用该装置改做“探究水和煤油吸热升温的快慢”的实验。为此,他们对装置及实验条件进行变换,一是甲、乙两烧瓶中安装的电阻丝的阻值
相等 (选填“相等”或“不相等”);二是将其中一烧瓶中的煤油换成
质量 和初温相等的水。
【解答】解:(1)根据控制变量法的要求知,甲、乙两烧瓶中装入质量相同、初温度相同的煤油,这样尽可能的使液体的散热快慢相同;
(2)实验过程中通过比较温度计示数的变化来反映电流产生热量的多少,这用到了转换法;
(3)两电阻串联,通电时间和电流相等,由焦耳定律Q=I2Rt得,电阻大的在相同时间产生的热量多,升高的温度快,由于R甲>R乙,所以甲烧瓶中温度计示数升高较快;
(4)利用该装置改做“探究水和煤油吸热升温的快慢”的实验,实际上是探究水和煤油比热容的大小,根据Q=cm△t,需要保持水和煤油吸收的热量、质量相同。要保持吸收热量的多少,就要保证电热相等,所以要保证电热丝的电阻阻值相等,所以需要在甲乙两烧瓶中安装的电阻丝的阻值相等,除此以外还将其中一烧瓶中的煤油换成质量和初温相等的水。
故答案为:(1)相同;相同;(2)温度计示数的变化;(3)电流;甲;(4)相等;质量。
9.如图所示是某实验小组探究“电流产生的热量与哪些因素有关”的实验装置。
(1)实验时,两瓶煤油的质量要
相等 ,在这个实验中,电流产生的热量的多少,是通过
温度计示数变化 体现出来。为了便于实验观察,还应使两瓶煤油的
初温 相同。
(2)图甲中,RA与RB采用串联的方式,其目的是为了控制通电时间、 电流 相等,选用的RA和RB的阻值大小
不相等 (选填“相等”或“不相等”),实验中选用煤油而不选用水,主要是因为水的
比热容 比煤油大。
(3)图甲探究的是电热与
电阻 的关系。按图乙方法进行实验时,观察到在相同的时间内C瓶煤油比D瓶煤油的温度上升更多,这说明:其他条件相同时, 电流 越大,电流通过导体产生的热量越多。
【解答】解:(1)根据控制变量法可知,实验前要使两瓶煤油的质量相等;
电流通过导体产生热量的多少,我们通过肉眼直接观察看不到其多少,在此应用了转换法,把电流通过导体产生热量的多少用我们能看到的现象表现出来,在该题中是通过温度计示数变化把电流通过导体产生热量的多少体现出来;
为了便于观察,实验前要使两瓶煤油的初温相等,通过温度计示数的变化来判断电流通过导体产生热量的多少;
(2)RA与RB采用串联的连接方式,目的是控制通过两电阻丝的电流相等,通电时间相同,所以探究的是电流产生的热量与电阻的关系,因此所选择的两段电阻丝的电阻大小应该不同;
因为煤油的比热容比水的小,相同质量的煤油和水比较,吸收相同的热量,煤油温度升高的多,用煤油做实验效果更明显;
(3)图甲中两电阻丝串联,电流相等,电阻不同,探究的是电热与电阻的关系;
乙装置中一个5Ω的电阻与两个5Ω的电阻并联后再串联,根据串联电路的电流特点可知,右端两个电阻的总电流和左端的电阻电流相等,即I右=I左,两个5Ω的电阻并联,根据并联电路的电流特点知I右=I1+I2,两电阻阻值相等,则支路中电流相等,I1=I2,所以右边容器中的通过电阻的电流是左侧通过电流的一半,因此通电一段时间后,在相同的时间内C瓶煤油比D瓶煤油的温度上升更多,说明在通电时间和电阻相同的情况下,电流越大,电流通过电阻丝产生的热量就越多。
故答案为:(1)相等;温度计示数变化;初温;(2)电流;不相等;比热容;(3)电阻;电流。
10.在“探究电流产生的热量与哪些因素有关”的实验中,实验电路如图1所示,其中R1>R2。
实验一:探究电流产生的热量与电阻大小的关系:
(1)请按照图1中的电路图将图2实物图连接完整;
(2)实验电路按照图1中的电路图连接是为了控制通电时间相同和控制
电流相同 ;电阻丝放出热量的多少,通过
温度计的示数变化 来进行判断。
(3)为了便于比较两根电阻丝通过电流后产生热量的多少,a、b两瓶中要装入
质量 相等、初温相同的同种液体。为了在较短时间内达到明显的实验效果,实验时选用煤油而不选水,是因为煤油的比热容
小于 水的比热容(选填“大于”、“等于”或“小于”)。
实验二:探究电流产生的热量与电流大小的关系:
(4)闭合开关,移动滑动变阻器的滑片,使电路中的电流变成实验一中电流的2倍,且通电时间相同。实验发现:用电阻丝R1加热的煤油,在实验一中温度升高△t1,在实验二中温度升高△t1′,则△t1′ 大于 2△t1(选填“大于”、“等于”或“小于”),该实验说明电流产生的热量与电流大小
不成 正比例关系(选填“成”或“不成”)。实验中,用电阻丝R2加热煤油重复以上实验步骤,也可以得出相同的结论。
(5)如果在两烧瓶中分别装入质量相等的不同液体,并接入两根阻值
相同 的电阻丝(选填“相同”或“不同”),就可用这个装置来探究两种不同液体的吸热性质。假设a烧瓶中液体的质量为m,瓶中电阻丝的阻值为R,测出通过它的电流为I,通电一段时间t后,温度计的示数变化量为△t,若不计热量损失,则a液体的比热容为
c= (用所给出的物理量写出比热容的表达式)。
【解答】解:(1)由电路图可知,滑片左移时变阻器接入电路中的电阻变小,则变阻器左下方接线柱必须接入电路中,如下图所示:
(2)由电路图可知,两电热丝串联在电路中,这是为了控制通电时间相同和控制电流相同;
根据转换法可知,电阻丝放出热量的多少,是通过温度计示数的变化进行比较的;
(3)为了便于比较两根电阻丝通过电流后产生热量的多少,a、b两瓶中要装入质量相等、初温相同的同种液体;
因为煤油的比热容比水的比热容小,相同质量的煤油和水比较,吸收相同的热量,煤油温度升高的多,用煤油做实验效果更明显,便于观察;
(4)闭合开关,移动滑动变阻器的滑片,使电路中的电流变成实验一中电流的2倍,且通电时间相同,
由Q=I2Rt可知,电阻丝产生的热量是原来的4倍,
由Q吸=cm△t的变形式△t=可知,用电阻丝R1加热的煤油,温度升高量△t1′大于2△t1,
该实验说明电流产生的热量与电流不成正比例关系;
(5)实验中两电阻丝串联,通过的电流和通电时间相同,为控制相同时间两液体吸热相同,根据Q=I2Rt可知,选用的两根电阻丝的阻值应相同;
假设a烧瓶中液体的质量为m,瓶中电阻丝的阻值为R,测出通过它的电流为I,通电一段时间t后,电热丝放出的热量Q=I2Rt,
温度计的示数变化量为△t,若不计热量损失,放出的热量全部被液体吸收,由Q吸=cm△t可得,a液体的比热容:c==。
故答案为:(1)如上图所示;(2)电流相同;温度计的示数变化;(3)质量;小于;(4)大于;不成;(4)相同;c=。
11.如图甲所示是小媛家新买的新型电热水壶,该电热水壶有加热、保温和干烧断电功能,其简化电路如图乙所示。S1是壶底温控开关,通常闭合,当壶底发热盘温度达到120℃自动断开,S2是壶壁温控开关,闭合时对水加热,断开时对水保温。已知电热水壶加热功率为1100W,保温功率为55W。求:
(1)电热水壶处于加热状态时,电路中的电流;
(2)电阻R2的阻值;
(3)若水烧开后,S2没有自动断开,当壶里的水烧干瞬间,发热盘的温度为110℃,已知发热盘质量为0.44kg,比热容为0.5×103J/(kg?℃),若水壶的加热效率为80%,则经过多长时间S1才会断开?
【解答】解:
(1)根据P=UI知电热水壶处于加热状态时,电路中的电流为:
I===5A;
(2)由图示和题意可知,当S1、S2闭合时,电路中只有R1工作,电热水壶处于加热状态,
根据P=知R1的阻值为:
R1===44Ω;
当S1闭合,S2断开时,R1与R2串联接入电路,电热水壶处于保温状态,
保温时电路的总电阻为:
R===880Ω,
由串联电路电阻的规律可知电阻R2的阻值为:
R2=R﹣R1=880Ω﹣44Ω=836Ω;
(3)当壶里的水烧干瞬间,发热盘的温度为110℃,当壶底发热盘温度达到120℃时S2自动断开,
该过程中发热盘吸收的热量为:
Q吸=cm(t﹣t0)=0.5×103J/(kg?℃)×0.44kg×(120℃﹣110℃)=2.2×103J,
根据η=得消耗的电能为:
W===2.75×103J,
根据P=得加热时间为:
t===2.5s,
所以当壶里的水烧干瞬间,经过2.5s的时间S1才会断开。
答:(1)电热水壶处于加热状态时,电路中的电流为5A;
(2)电阻R2的阻值为836Ω;
(3)若水烧开后,S2没有自动断开,当壶里的水烧干瞬间,经过2.5s的时间S1才会断开。
12.智能全自动茶炉(如图)内有加热电阻,集抽水、烧水、保温于一体,美观大方,容易操作,如表为某款智能全自动茶炉的部分参数。[ρ水=1.0×103kg/m3,c水=4.2×103J/(kg?℃)]求:
产品名称
智能全自动茶炉
产品型号
XXXX
烧水功率
1210W
容量
0.8L
保温功率
22W
额定电压
220V
(1)将一壶水从20℃加热到70℃,水吸收的热量。
(2)保温状态下通过茶炉的电流。
(3)若用电高峰时,家庭电路的实际电压仅为200V,求该茶炉的实际加热功率(加热电阻阻值不变)。
【解答】解:(1)根据ρ=知水的质量为:
m=ρ水V=1.0×103kg/m3×0.8×10﹣3m3=0.8kg,
水吸热的热量为:
Q吸=c水m(t﹣t0)
=4.2×103J/(kg?℃)×0.8kg×(70℃﹣20℃)
=1.68×105J;
(2)根据P=UI知保温状态下通过茶炉的电流为:
I保温===0.1A;
(3)根据P=知加热电阻为:
R===40Ω,
该茶炉的实际加热功率为:
P实===1000W。
答:(1)将一壶水从20℃加热到70℃,水吸收的热量为1.68×105J;
(2)保温状态下通过茶炉的电流为0.1A;
(3)该茶炉的实际加热功率为1000W。
13.如图所示是某电热器装置的简化电路图,开关S可切换加热和保温两种状态,它的额定电压为220V,额定加热功率是P热=1100W,R1、R2是发热电阻,R2=440Ω。已知电路电压正常,已知水的比热容为4.2×103J/(kg?℃),试完成下列问题:
(1)图中电阻R1的阻值是多大?
(2)该电热器的保温功率P温是多大?
(3)若该电热器将2kg的水从20℃,加热到75℃,需要8min时间,则它加热时将电能转化为水的内能的效率为多少?
【解答】解:(1)当开关S接a时,为R1的简单电路;S接b时,两电阻串联,
因根据串联总电阻大于其中任一电阻,根据P=可知,当开关S接a时,电热器为加热状态;当开关S接b时,电阻R1和R2串联,电热器为保温状态;
由P=可得,电阻R1的阻值:
R1===44Ω;
(2)当开关S接b时,电阻R1和R2串联,为保温状态,
根据P=和电阻的串联知保温功率为:
P保温===100W;
(3)水的初温为20℃,使水的温度升高到75℃,水吸收的热量为:
Q吸=c水m△t=4.2×103J/(kg?℃)×2kg×(75℃﹣20℃)=4.62×105J;
电热器正常工作加热8min消耗的电能:
W=P加热t=1100W×8×60s=5.28×105J;
电热装置的加热效率:
η=×100%×100%=87.5%。
答:(1)图中电阻R1的阻值是44Ω;
(2)该电热器的保温功率P温是100W;
(3)该加热器加热时将电能转化为水的内能的效率为87.5%。
14.多功能养生壶具有精细烹饪、营养量化等功能,深受市场认可和欢迎,如图乙所示是某品牌养生壶简化电路图。
[ρ水=1×103kg/m3,c水=4.2×103J/(kg?℃)]
中温挡功率/W
550
高温挡功率/W
1100
容积/L
1
(1)求R1的阻值。
(2)养生壶在低温挡工作时,求电路中的电流大小。
(3)在标准大气压下,使用高温挡将初温是12℃的一壶水烧开,若养生壶高温挡加热效率为80%,求烧开一壶水需要的时间。
【解答】解:
(1)由图知,当开关S1闭合,S2接B时,电阻R1、R2并联,电路中的总电阻最小,由P=可知,总功率最大,所以此状态为高温挡;
由图知,当开关S1断开,S2接A时,电阻R1、R2串联,电路中的总电阻最大,由P=可知,总功率最小,此时为低温挡;
当S2接A,S1闭合时,R2被短路,只有电阻R1接入电路,养生壶处于中温挡。
由P=UI得,正常工作时通过R1的电流为:I1===2.5A,
由I=得,R1的阻值:R1===88Ω;
(2)因高温挡和中温挡时R1均工作,且两种状态下R1两端电压和电阻均不变,则R1消耗的功率不变,所以高温挡时R2的功率:P2=P高﹣P中=1100W﹣550W=550W,
由P=可知,R2的阻值:R2===88Ω,
由串联电路电阻规律可知,养生壶在低温挡工作时,电路中的电流:I低===1.25A;
(3)由ρ=可得,水的质量:m=ρ水V=1.0×103kg/m3×1×10﹣3m3=1kg,
水吸收的热量:Q吸=c水m△t=4.2×103J/(kg?℃)×1kg×(100℃﹣12℃)=3.696×105J,
由η=可得,养生壶消耗的电能:W===4.62×105J,
由P=可得,烧开一壶水需要的时间:t===420s。
答:(1)R1的阻值为88Ω。
(2)养生壶在低温挡工作时,电路中的电流为1.25A。
(3)烧开一壶水需要的时间为420s。
15.如图是小灵家新购买的电热水器的简化原理图,R1和R2为定值电阻,S为温控开关,a、b是开关的连接触点,电热水器部分参数如表所示。求:
额定电压
220V
加热功率
2000W
保温功率
200W
(1)当把25kg的水由20℃加热到60℃时,水吸收的热量;若热水器加热时的效率为80%,需要消耗的电能。[c水=4.2×103J/(kg?℃)]
(2)R2的阻值。
【解答】解:(1)使水温由20℃升高到60℃,水需要吸收热量为:
Q吸=c水m(t﹣t0)=4.2×103J/(kg?℃)×25kg×(60℃﹣20℃)=4.2×106J;
根据η=得消耗的电能为:
W===5.25×106J;
(2)由电路图可知,开关S与触点a连通时电路为R1的简单电路,开关S与触点b连通时R1与R2串联,
因串联电路中总电阻等于各分电阻之和,
所以,开关S与触点a连通时,电路的总电阻最小,
电源的电压一定,由P=可知,此时电路的总功率最大,热水器处于加热状态;
反之,开关S与触点b连通时,电路的总电阻最大,总功率最小,热水器处于保温状态;
R1的阻值:
R1===24.2Ω,
热水器处于保温状态时,R1与R2串联,此时电路的总电阻:
R===242Ω,
因串联电路中总电阻等于各分电阻之和,
R2的阻值:
R2=R﹣R1=242Ω﹣24.2Ω=217.8Ω。
答:(1)当把25kg的水由20℃加热到60℃时,水吸收的热量为4.2×106J;
若热水器加热时的效率为80%,需要消耗的电能为5.25×106J;
(2)R2的阻值为217.8Ω。
16.甲、乙两个电热器的电阻之比为2:3,通电相同时间产生的热量之比为6:1,则通过甲、乙的电流之比为( )
A.3:1
B.1:3
C.3:2
D.2:3
【解答】解:由题意可知,R甲:R乙=2:3,t甲:t乙=1:1,Q甲:Q乙=6:1,
由Q=I2Rt可得,通过甲、乙的电流之比:
====。
故选:A。
17.甲乙两电热器通过的电流之比为3:2,通电时间之比为2:3,电阻之比为4:3,则产生热量之比为( )
A.1:2
B.2:9
C.2:1
D.9:2
【解答】解:由题意可知,I甲:I乙=3:2,t甲:t乙=2:3,R甲:R乙=4:3,
由Q=I2Rt可得,电流通过甲、乙两个电热器产生的热量之比:
==()2××=()2××=。
故选:C。
18.一阻值为R的电阻丝接在电压为U的电路中,在t时间内放出的热量为Q,现把该电阻丝对折起来接到原来的电路中,放出同样多的热量,需要的时间是( )
A.
B.
C.t
D.2t
【解答】解:导体的电阻与导体的材料、长度,横截面积有关,材料相同时,长度越长,横截面积越小,电阻越大,
该电阻丝对折起来,横截面积变为原来的2倍,长度变为原来的,电阻变为原来的,
根据焦耳定律的变形公式可知原来放出的热量为Q=,
对折起来接到原来的电路中,放出同样多的热量,需要的时间是:t′==t。
故选:A。
19.甲、乙两段导体通电时间相同,甲的电阻是乙的3倍,甲、乙产生的热量之比是4:3,则通过甲、乙两导体的电流之比是( )
A.2:3
B.2:1
C.9:2
D.3:2
【解答】解:由题知,甲、乙两段导体通电时间相同,甲的电阻是乙的3倍,即R甲=3R乙,甲、乙产生的热量之比是4:3,即3Q甲=4Q乙,
由Q=I2Rt有:3I甲2R甲t=4I乙2R乙t,
即:3I甲2×3R乙t=4I乙2R乙t
所以9I甲2=4I乙2,
=。
故选:A。
20.某一阻值为R的电阻,通过的电流为I时,在t时间内产生的热量是Q。则当另一阻值为2R的电阻,通过电流是2I时,在同样的t时间内产生的热量为( )
A.2Q
B.4Q
C.8Q
D.16Q
【解答】解:由题知,阻值为R的电阻,通过的电流为I时,在t时间内产生的热量是Q,
由焦耳定律有:Q=I2Rt,
当另一阻值为2R的电阻,通过电流是2I时,在同样的t时间内产生的热量:
Q'=(2I)2×2R×t=8I2Rt=8Q。
故选:C。
考点一.焦耳定律应用
1.如图所示,给电炉通电后,电炉丝热得发红,而用手触摸与之连接的导线却不觉得烫手,这是因为( )
A.电流通过导线时没有产生热效应
B.通过电炉丝的电流比通过导线的电流大得多
C.电炉丝的电阻比导线的电阻小得多
D.电炉丝消耗的电功率比导线消耗的电功率大得多
2.将口香糖的锡箔纸包装剥下来,用小刀剪成约5mm宽、10cm长的细条,做成两头宽、中间窄的纺锤形状(如图所示)。再把锡箔纸两头有亮光的一面(锡箔),分别用手摁在干电池的正负极上,3秒钟左右,锡箔纸中间狭窄部分即开始燃烧起来。关于此情景下列说法中正确的是( )
A.锡箔燃烧是因为此处电流较大
B.相同长度锡箔较窄处的电阻较小
C.锡箔中电子从电池正极流向负极
D.相同长度锡箔较窄处的电压较大
3.小明发现当给家中的电灯通电后,灯丝热得发光,而与灯泡串联的导线温度几乎感觉不到变化,对这一现象的解释,正确的是( )
A.通过灯丝的电流大些
B.电流在导线中不发生热效应
C.制成灯丝的材料电阻较小
D.导线和灯丝中的电流相同,但灯丝电阻更大
考点二.探究电流通过导体时产生的热量与什么因素有关
4.在做“探究电流通过导体时产生的热量与什么因素有关”的实验时,小龙采用了如图所示的实验装置。(两个透明容器中封闭着等量气体)
(1)在实验过程中,通过观察U形管中
的变化来比较电流通过电阻丝产生热量的多少。
(2)图甲所示的装置是用来探究电流通过电阻丝产生的热量与
的关系。
(3)图乙所示的装置是用来探究电流通过电阻丝产生的热量与
的关系。
(4)综合分析图甲、乙两装置的实验现象,可以得出的结论是:电流通过导体产生热量与通过导体的电流和电阻大小有关,通过导体的电流越大,导体的电阻越大,产生的热量
。
5.如图所示,探究影响电流热效应的因素。
(1)烧瓶内安装一根电阻丝,插入一支温度计,比较烧瓶内液体温度的变化,判断相同时间内不同电流产生的热量多少。要使烧瓶内液体短时间内温度变化更明显,应选用
(选填“煤油”或“水”)。
(2)测得烧瓶内液体的温度,闭合开关,通电30s再测量烧瓶内液体的温度,得到温度的升高量;改变电流大小,重复操作,数据记录表中。实验表明,同一导体,通电时间相等时,电流越
,产生的热量越
。
实验次数
电流I/A
通电时间t/s
电阻R/Ω
温度升高量/℃
1
0.3
30
10
1.5
2
0.6
30
10
6.0
(3)探究电热器产生热量与电阻的关系,应保持电流和通电时间相等,同时选择图
(选填“A”或“B”)烧瓶
(选填“串联”或“并联”)接进电路。
6.在探究“电流通过导体产生热量的多少与哪些因素有关”的实验中,采用了如下电路。
(1)为了在短时间内达到明显的实验效果,两烧瓶中应装入质量和初温都相同的
(选填“水”或“煤油”),实验中通过观察
来比较电流通过导体产生热量的多少;
(2)如图甲所示,两烧瓶中装有阻值不同的电热丝,可以探究电流通过导体产生的热量与
的关系;
(3)如图乙所示,两烧瓶中装有阻值相同的电热丝,闭合开关,调节滑动变阻器,使两电流表示数
(选填“相同”或“不同”),可以探究电流通过导体产生的热量与
的关系。
7.小组同学选择阻值不变的电阻丝,探究“电流通过电阻丝产生的热量(简称电热)与通电时间、电流、电阻的关系”。
(1)为探究电热与通电时间、电流的关系,在锥形瓶内装入适量煤油,设计电路如图甲所示,开关闭合前,滑动变阻器的滑片P应置于
(A/B)端。
(a)闭合开关S,调节滑动变阻器的滑片P,直至电流表示数为0.5A,通电5分钟、温度计的示数升高了5℃。
(b)保持滑动变阻器滑片P的位置不变,通电10分钟、温度计的示数升高了9℃。
(a)、(b)对比可得结论:
。
(c)向
移动滑动变阻器的滑片P,直至电流表示数为1A,通电10分钟、温度计的示数升高了33℃,(b)、(c)对比可得结论:
。
(d)实验只能得到定性结论,主要原因是
。
(2)为探究电热与电阻的关系,并测出标签污损的电阻丝R2的阻值,在两个相同的锥形瓶内装入等质量的煤油,设计如图乙所示电路。开关闭合后,电压表有示数,但电流表无示数,电路故障是
,排除故障后,调节滑动变阻器的滑片P得到电表示数如图丙所示,则电压表示数为
Ⅴ,电流表示数为
A,R2阻值为
Ω。一段时间后,观察到电阻丝
所在锥形瓶中的温度计示数升高的比较多。
(3)请分析“电炉工作时,电炉丝发热明显、而与电炉丝相连的导线发热不明显”:电炉丝的电流
导线的电流,电炉丝的电阻
导线的电阻。(选填:“大于”、“等于”、“小于”)
8.小明用如图所示的装置探究电流产生的热量与电阻的关系。已知R甲>R乙,烧瓶及配属装置的材料、规格相同。
(1)甲、乙两烧瓶中装入质量
的煤油。考虑到热效率尽可能相等的问题,甲、乙两烧瓶中液体的初温应该
(选填“相同”或“不同”)。
(2)实验过程中通过比较
(选填“温度计示数的变化”或“加热时间”)来反映电流产生热量的多少。
(3)电阻丝R甲与R乙采用串联接入电路的方法,保证了可能相关因素
的大小及通电时间相同。闭合开关,通电一段时间后,观察发现
瓶中煤油吸收的热量更多。
(4)小华提议,利用该装置改做“探究水和煤油吸热升温的快慢”的实验。为此,他们对装置及实验条件进行变换,一是甲、乙两烧瓶中安装的电阻丝的阻值
(选填“相等”或“不相等”);二是将其中一烧瓶中的煤油换成
和初温相等的水。
9.如图所示是某实验小组探究“电流产生的热量与哪些因素有关”的实验装置。
(1)实验时,两瓶煤油的质量要
,在这个实验中,电流产生的热量的多少,是通过
体现出来。为了便于实验观察,还应使两瓶煤油的
相同。
(2)图甲中,RA与RB采用串联的方式,其目的是为了控制通电时间、
相等,选用的RA和RB的阻值大小
(选填“相等”或“不相等”),实验中选用煤油而不选用水,主要是因为水的
比煤油大。
(3)图甲探究的是电热与
的关系。按图乙方法进行实验时,观察到在相同的时间内C瓶煤油比D瓶煤油的温度上升更多,这说明:其他条件相同时,
越大,电流通过导体产生的热量越多。
10.在“探究电流产生的热量与哪些因素有关”的实验中,实验电路如图1所示,其中R1>R2。
实验一:探究电流产生的热量与电阻大小的关系:
(1)请按照图1中的电路图将图2实物图连接完整;
(2)实验电路按照图1中的电路图连接是为了控制通电时间相同和控制
;电阻丝放出热量的多少,通过
来进行判断。
(3)为了便于比较两根电阻丝通过电流后产生热量的多少,a、b两瓶中要装入
相等、初温相同的同种液体。为了在较短时间内达到明显的实验效果,实验时选用煤油而不选水,是因为煤油的比热容
水的比热容(选填“大于”、“等于”或“小于”)。
实验二:探究电流产生的热量与电流大小的关系:
(4)闭合开关,移动滑动变阻器的滑片,使电路中的电流变成实验一中电流的2倍,且通电时间相同。实验发现:用电阻丝R1加热的煤油,在实验一中温度升高△t1,在实验二中温度升高△t1′,则△t1′
2△t1(选填“大于”、“等于”或“小于”),该实验说明电流产生的热量与电流大小
正比例关系(选填“成”或“不成”)。实验中,用电阻丝R2加热煤油重复以上实验步骤,也可以得出相同的结论。
(5)如果在两烧瓶中分别装入质量相等的不同液体,并接入两根阻值
的电阻丝(选填“相同”或“不同”),就可用这个装置来探究两种不同液体的吸热性质。假设a烧瓶中液体的质量为m,瓶中电阻丝的阻值为R,测出通过它的电流为I,通电一段时间t后,温度计的示数变化量为△t,若不计热量损失,则a液体的比热容为
(用所给出的物理量写出比热容的表达式)。
考点三.电热综合计算
11.如图甲所示是小媛家新买的新型电热水壶,该电热水壶有加热、保温和干烧断电功能,其简化电路如图乙所示。S1是壶底温控开关,通常闭合,当壶底发热盘温度达到120℃自动断开,S2是壶壁温控开关,闭合时对水加热,断开时对水保温。已知电热水壶加热功率为1100W,保温功率为55W。求:
(1)电热水壶处于加热状态时,电路中的电流;
(2)电阻R2的阻值;
(3)若水烧开后,S2没有自动断开,当壶里的水烧干瞬间,发热盘的温度为110℃,已知发热盘质量为0.44kg,比热容为0.5×103J/(kg?℃),若水壶的加热效率为80%,则经过多长时间S1才会断开?
12.智能全自动茶炉(如图)内有加热电阻,集抽水、烧水、保温于一体,美观大方,容易操作,如表为某款智能全自动茶炉的部分参数。[ρ水=1.0×103kg/m3,c水=4.2×103J/(kg?℃)]求:
产品名称
智能全自动茶炉
产品型号
XXXX
烧水功率
1210W
容量
0.8L
保温功率
22W
额定电压
220V
(1)将一壶水从20℃加热到70℃,水吸收的热量。
(2)保温状态下通过茶炉的电流。
(3)若用电高峰时,家庭电路的实际电压仅为200V,求该茶炉的实际加热功率(加热电阻阻值不变)。
13.如图所示是某电热器装置的简化电路图,开关S可切换加热和保温两种状态,它的额定电压为220V,额定加热功率是P热=1100W,R1、R2是发热电阻,R2=440Ω。已知电路电压正常,已知水的比热容为4.2×103J/(kg?℃),试完成下列问题:
(1)图中电阻R1的阻值是多大?
(2)该电热器的保温功率P温是多大?
(3)若该电热器将2kg的水从20℃,加热到75℃,需要8min时间,则它加热时将电能转化为水的内能的效率为多少?
14.多功能养生壶具有精细烹饪、营养量化等功能,深受市场认可和欢迎,如图乙所示是某品牌养生壶简化电路图。
[ρ水=1×103kg/m3,c水=4.2×103J/(kg?℃)]
中温挡功率/W
550
高温挡功率/W
1100
容积/L
1
(1)求R1的阻值。
(2)养生壶在低温挡工作时,求电路中的电流大小。
(3)在标准大气压下,使用高温挡将初温是12℃的一壶水烧开,若养生壶高温挡加热效率为80%,求烧开一壶水需要的时间。
15.如图是小灵家新购买的电热水器的简化原理图,R1和R2为定值电阻,S为温控开关,a、b是开关的连接触点,电热水器部分参数如表所示。求:
额定电压
220V
加热功率
2000W
保温功率
200W
(1)当把25kg的水由20℃加热到60℃时,水吸收的热量;若热水器加热时的效率为80%,需要消耗的电能。[c水=4.2×103J/(kg?℃)]
(2)R2的阻值。
考点四.比值计算
16.甲、乙两个电热器的电阻之比为2:3,通电相同时间产生的热量之比为6:1,则通过甲、乙的电流之比为( )
A.3:1
B.1:3
C.3:2
D.2:3
17.甲乙两电热器通过的电流之比为3:2,通电时间之比为2:3,电阻之比为4:3,则产生热量之比为( )
A.1:2
B.2:9
C.2:1
D.9:2
18.一阻值为R的电阻丝接在电压为U的电路中,在t时间内放出的热量为Q,现把该电阻丝对折起来接到原来的电路中,放出同样多的热量,需要的时间是( )
A.
B.
C.t
D.2t
19.甲、乙两段导体通电时间相同,甲的电阻是乙的3倍,甲、乙产生的热量之比是4:3,则通过甲、乙两导体的电流之比是( )
A.2:3
B.2:1
C.9:2
D.3:2
20.某一阻值为R的电阻,通过的电流为I时,在t时间内产生的热量是Q。则当另一阻值为2R的电阻,通过电流是2I时,在同样的t时间内产生的热量为( )
A.2Q
B.4Q
C.8Q
D.16Q
2021人教版九年级物理18.4焦耳定律考点
参考答案
1.如图所示,给电炉通电后,电炉丝热得发红,而用手触摸与之连接的导线却不觉得烫手,这是因为( )
A.电流通过导线时没有产生热效应
B.通过电炉丝的电流比通过导线的电流大得多
C.电炉丝的电阻比导线的电阻小得多
D.电炉丝消耗的电功率比导线消耗的电功率大得多
【解答】解:A、由于导线有电阻,电流通过导线时,导线会发热,产生热效应,故A错误;
BCD、电炉在使用时,电炉丝和导线串联,通过它们的电流相等,通电时间t相同,由于R电炉丝>R导线,根据Q=I2Rt可知,电流产生的热量:Q电炉丝>Q导线,根据P=I2R知,导线消耗的电功率比电炉丝消耗的电功率小,因而出现电炉丝热得发红,而与电炉丝相连的导线却不怎么发热的现象;故BC错误,D正确。
故选:D。
2.将口香糖的锡箔纸包装剥下来,用小刀剪成约5mm宽、10cm长的细条,做成两头宽、中间窄的纺锤形状(如图所示)。再把锡箔纸两头有亮光的一面(锡箔),分别用手摁在干电池的正负极上,3秒钟左右,锡箔纸中间狭窄部分即开始燃烧起来。关于此情景下列说法中正确的是( )
A.锡箔燃烧是因为此处电流较大
B.相同长度锡箔较窄处的电阻较小
C.锡箔中电子从电池正极流向负极
D.相同长度锡箔较窄处的电压较大
【解答】解:
A、由图可知,锡箔纸中间燃烧部分与两头是串联的,由串联电路的电流特点可知燃烧部分与两头的电流相等,故A错误;
B、长度和材料相同时,较窄处横截面积较小,其电阻较大,故B错误;
C、在电源外部,电流从电源正极流出经锡箔纸回到电源负极;而电子定向移动的方向与电流方向相反,所以电子从负极经锡箔纸流向正极,故C错误;
D、由B选项知,较窄处电阻较大,电流相等,由U=IR可知,较窄处的电压较大,故D正确。
故选:D。
3.小明发现当给家中的电灯通电后,灯丝热得发光,而与灯泡串联的导线温度几乎感觉不到变化,对这一现象的解释,正确的是( )
A.通过灯丝的电流大些
B.电流在导线中不发生热效应
C.制成灯丝的材料电阻较小
D.导线和灯丝中的电流相同,但灯丝电阻更大
【解答】解:因为灯丝和导线串联,所以通过灯丝和导线的电流、通电时间都相同,根据焦耳定律Q=I2Rt,灯丝电阻大,产生热量多,而导线电阻非常小,产生的热量就很小,所以电灯通电后,灯丝热得发光,而与灯泡串联的导线温度几乎感觉不到变化。故选项A、B、C都不正确,D选项正确。
故选:D。
4.在做“探究电流通过导体时产生的热量与什么因素有关”的实验时,小龙采用了如图所示的实验装置。(两个透明容器中封闭着等量气体)
(1)在实验过程中,通过观察U形管中
液面高度 的变化来比较电流通过电阻丝产生热量的多少。
(2)图甲所示的装置是用来探究电流通过电阻丝产生的热量与
电阻 的关系。
(3)图乙所示的装置是用来探究电流通过电阻丝产生的热量与
电流 的关系。
(4)综合分析图甲、乙两装置的实验现象,可以得出的结论是:电流通过导体产生热量与通过导体的电流和电阻大小有关,通过导体的电流越大,导体的电阻越大,产生的热量
越多 。
【解答】解:(1)电流通过导体产生热量的多少不能直接观察,可以利用转换法,在实验过程中,通过观察U形管中液面高度的变化来比较电流通过电阻丝产生热量的多少;
(2)如图甲,两个电阻串联在电路中,通过的电流相同,通电时间相同,电阻不同,由控制变量法的要求可知,图甲是探究电流产生热量跟电阻大小的关系;
(3)图乙装置中是两个5Ω的电阻并联之后再与一个5Ω的电阻串联,根据串并联电路的电流特点可知,右端两个电阻的总电流和左端的电阻通过的电流相等,则左端容器中电阻通过的电流大于右端容器中电阻通过的电流,由于两个容器内的电阻阻值相同,通电时间相同,而电流不同,由控制变量法的要求可知,图乙是探究电流产生热量跟电流的关系;
(4)综合分析图甲和图乙两装置的实验现象,可以得出的结论:电流通过导体产生的热量与通过导体的电流和电阻大小有关,通过导体的电流越大,导体的电阻越大,产生的热量越多。
故答案为:(1)液面高度;(2)电阻;(3)电流;(4)越多。
5.如图所示,探究影响电流热效应的因素。
(1)烧瓶内安装一根电阻丝,插入一支温度计,比较烧瓶内液体温度的变化,判断相同时间内不同电流产生的热量多少。要使烧瓶内液体短时间内温度变化更明显,应选用
煤油 (选填“煤油”或“水”)。
(2)测得烧瓶内液体的温度,闭合开关,通电30s再测量烧瓶内液体的温度,得到温度的升高量;改变电流大小,重复操作,数据记录表中。实验表明,同一导体,通电时间相等时,电流越
大 ,产生的热量越
多 。
实验次数
电流I/A
通电时间t/s
电阻R/Ω
温度升高量/℃
1
0.3
30
10
1.5
2
0.6
30
10
6.0
(3)探究电热器产生热量与电阻的关系,应保持电流和通电时间相等,同时选择图
(选填“A”或“B”)烧瓶
串联 (选填“串联”或“并联”)接进电路。
【解答】解:(1)由于煤油的比热容较小,质量相同吸收热量相同时,温度变化比较明显,应选用煤油进行实验;
(2)由表格中数据知,通电时间和电阻相等,电流增大为原来的2倍,温度升高为原来的4倍,即产生的热量为原来的4倍,可知通电时间和电阻相等,电流越大,产生的热量越多,产生的热量与电流的2次方成正比;
(3)若要探究电热器产生热量与电阻的关系,应保持电流和通电时间相等,电阻不同,所以应该选择B烧瓶和甲图中的烧瓶串联。
故答案为:(1)煤油;(2)大;多;(3)B;串联。
6.在探究“电流通过导体产生热量的多少与哪些因素有关”的实验中,采用了如下电路。
(1)为了在短时间内达到明显的实验效果,两烧瓶中应装入质量和初温都相同的
煤油 (选填“水”或“煤油”),实验中通过观察
两支温度计示数变化 来比较电流通过导体产生热量的多少;
(2)如图甲所示,两烧瓶中装有阻值不同的电热丝,可以探究电流通过导体产生的热量与
电阻 的关系;
(3)如图乙所示,两烧瓶中装有阻值相同的电热丝,闭合开关,调节滑动变阻器,使两电流表示数
不同 (选填“相同”或“不同”),可以探究电流通过导体产生的热量与
电流 的关系。
【解答】解:(1)根据Q吸=cm△t
知,只有两个烧瓶中装入初温度和质量均相同的煤油时,才能通过煤油的温度变化量来反映电流产生热量的多少;
若将烧瓶中装有水,则由Q=cm△t可知:在相同质量的水和煤油中,吸收的相同的热量时,由于水的比热容大,温度升高的度数少,温度计的示数变化不明显,故为了实验效果明显,应选用质量相同的煤油而不用水;
实验中通过观察两支温度计示数变化来比较电流产生的热量的多少,这用到了转换法;
(2)如图甲所示,两电阻串联,通过两电阻的电流和通电时间相同,改变电阻,可以探究电流通过导体产生的热量与电阻的关系;
(3)如图乙所示,两烧瓶中装有阻值相同的电热丝,闭合开关,控制电阻和通电时间相同,通过调节滑动变阻器改变电路的电流,观察同一只烧瓶中煤油升高的温度计的示数变化,可以探究电流通过导体产生的热量与电流的关系。
故答案为:(1)煤油;两支温度计示数变化;(2)电阻;(3)不同;电流。
7.小组同学选择阻值不变的电阻丝,探究“电流通过电阻丝产生的热量(简称电热)与通电时间、电流、电阻的关系”。
(1)为探究电热与通电时间、电流的关系,在锥形瓶内装入适量煤油,设计电路如图甲所示,开关闭合前,滑动变阻器的滑片P应置于
(A/B)端。
(a)闭合开关S,调节滑动变阻器的滑片P,直至电流表示数为0.5A,通电5分钟、温度计的示数升高了5℃。
(b)保持滑动变阻器滑片P的位置不变,通电10分钟、温度计的示数升高了9℃。
(a)、(b)对比可得结论: 在电流大小和电阻大小相同时,通电时间越长,电流通过电阻产生的热量越多 。
(c)向
A端 移动滑动变阻器的滑片P,直至电流表示数为1A,通电10分钟、温度计的示数升高了33℃,(b)、(c)对比可得结论: 在通电时间和电阻大小相同时,电流越大,电流通过电阻产生的热量越多 。
(d)实验只能得到定性结论,主要原因是
实验中只能通过温度计示数的变化量来反映电流通过电阻产生的热量的多少,无法精确测量电阻产生的热量 。
(2)为探究电热与电阻的关系,并测出标签污损的电阻丝R2的阻值,在两个相同的锥形瓶内装入等质量的煤油,设计如图乙所示电路。开关闭合后,电压表有示数,但电流表无示数,电路故障是
R2断路 ,排除故障后,调节滑动变阻器的滑片P得到电表示数如图丙所示,则电压表示数为
8 Ⅴ,电流表示数为
0.5 A,R2阻值为
16 Ω。一段时间后,观察到电阻丝
R2 所在锥形瓶中的温度计示数升高的比较多。
(3)请分析“电炉工作时,电炉丝发热明显、而与电炉丝相连的导线发热不明显”:电炉丝的电流
等于 导线的电流,电炉丝的电阻
大于 导线的电阻。(选填:“大于”、“等于”、“小于”)
【解答】解:(1)滑动变阻器有保护电路的作用,开关闭合前,滑动变阻器的滑片P应置于阻值最大处,故位于B端;
(b)两次实验中,电阻和电流大小均相同,通电时间不同,(b)中温度计升高的示数较大,说明电流通过电阻产生的热量多,可得结论:在电流大小和电阻大小相同时,通电时间越长,电流通过电阻产生的热量越多;
(c)(c)实验中电流表示数变大,根据欧姆定律可知电路中的总电阻变小,滑动变阻器接入电路中的电阻变小,故应向A端移动滑片;
(b)、(c)两次实验中,电阻大小和通电时间均相同,(c)中电流大于(b)中电流,且温度计升高的示数较大,说明电流通过电阻产生的热量多,可得结论:在通电时间和电阻大小相同时,电流越大,电流通过电阻产生的热量越多;
(d)实验只能得到定性结论,主要原因是实验中只能通过温度计示数的变化量来反映电流通过电阻产生的热量的多少,无法精确测量电阻产生的热量;
(2)开关闭合后,电压表有示数,说明电压表与电源接通,但电流表无示数,说明电路中有断路的地方,电路故障是R2断路;
从图乙中可知,闭合开关后,两电阻丝和滑动变阻器串联,电流表测量电路电流,电压表测量R2两端的电压。
电压表选择大量程,分度值为0.5V,示数为8V,电流表选择小量程,分度值为0.02A,示数为0.5A;
根据欧姆定律可知R2的阻值R2===16Ω;
已知R1=10Ω<R2,根据Q=I2Rt可知一段时间后,电阻丝R2产生的热量多,故观察到电阻丝R2所在锥形瓶中的温度计示数升高的比较多;
(3)电炉丝和导线串联,故电炉丝的电流等于导线的电流,电炉丝的电阻大于导线的电阻,根据Q=I2Rt可知通电相同时间,电炉丝产生的热量大于导线产生的热量,故电炉工作时,电炉丝发热明显、而与电炉丝相连的导线发热不明显。
故答案为:(1)B;(b)在电流大小和电阻大小相同时,通电时间越长,电流通过电阻产生的热量越多;(c)A端;在通电时间和电阻大小相同时,电流越大,电流通过电阻产生的热量越多;(d)实验中只能通过温度计示数的变化量来反映电流通过电阻产生的热量的多少,无法精确测量电阻产生的热量;
(2)R2断路;8;0.5;16;R2;(3)等于;大于。
8.小明用如图所示的装置探究电流产生的热量与电阻的关系。已知R甲>R乙,烧瓶及配属装置的材料、规格相同。
(1)甲、乙两烧瓶中装入质量
相同 的煤油。考虑到热效率尽可能相等的问题,甲、乙两烧瓶中液体的初温应该
相同 (选填“相同”或“不同”)。
(2)实验过程中通过比较
温度计示数的变化 (选填“温度计示数的变化”或“加热时间”)来反映电流产生热量的多少。
(3)电阻丝R甲与R乙采用串联接入电路的方法,保证了可能相关因素
电流 的大小及通电时间相同。闭合开关,通电一段时间后,观察发现
甲 瓶中煤油吸收的热量更多。
(4)小华提议,利用该装置改做“探究水和煤油吸热升温的快慢”的实验。为此,他们对装置及实验条件进行变换,一是甲、乙两烧瓶中安装的电阻丝的阻值
相等 (选填“相等”或“不相等”);二是将其中一烧瓶中的煤油换成
质量 和初温相等的水。
【解答】解:(1)根据控制变量法的要求知,甲、乙两烧瓶中装入质量相同、初温度相同的煤油,这样尽可能的使液体的散热快慢相同;
(2)实验过程中通过比较温度计示数的变化来反映电流产生热量的多少,这用到了转换法;
(3)两电阻串联,通电时间和电流相等,由焦耳定律Q=I2Rt得,电阻大的在相同时间产生的热量多,升高的温度快,由于R甲>R乙,所以甲烧瓶中温度计示数升高较快;
(4)利用该装置改做“探究水和煤油吸热升温的快慢”的实验,实际上是探究水和煤油比热容的大小,根据Q=cm△t,需要保持水和煤油吸收的热量、质量相同。要保持吸收热量的多少,就要保证电热相等,所以要保证电热丝的电阻阻值相等,所以需要在甲乙两烧瓶中安装的电阻丝的阻值相等,除此以外还将其中一烧瓶中的煤油换成质量和初温相等的水。
故答案为:(1)相同;相同;(2)温度计示数的变化;(3)电流;甲;(4)相等;质量。
9.如图所示是某实验小组探究“电流产生的热量与哪些因素有关”的实验装置。
(1)实验时,两瓶煤油的质量要
相等 ,在这个实验中,电流产生的热量的多少,是通过
温度计示数变化 体现出来。为了便于实验观察,还应使两瓶煤油的
初温 相同。
(2)图甲中,RA与RB采用串联的方式,其目的是为了控制通电时间、 电流 相等,选用的RA和RB的阻值大小
不相等 (选填“相等”或“不相等”),实验中选用煤油而不选用水,主要是因为水的
比热容 比煤油大。
(3)图甲探究的是电热与
电阻 的关系。按图乙方法进行实验时,观察到在相同的时间内C瓶煤油比D瓶煤油的温度上升更多,这说明:其他条件相同时, 电流 越大,电流通过导体产生的热量越多。
【解答】解:(1)根据控制变量法可知,实验前要使两瓶煤油的质量相等;
电流通过导体产生热量的多少,我们通过肉眼直接观察看不到其多少,在此应用了转换法,把电流通过导体产生热量的多少用我们能看到的现象表现出来,在该题中是通过温度计示数变化把电流通过导体产生热量的多少体现出来;
为了便于观察,实验前要使两瓶煤油的初温相等,通过温度计示数的变化来判断电流通过导体产生热量的多少;
(2)RA与RB采用串联的连接方式,目的是控制通过两电阻丝的电流相等,通电时间相同,所以探究的是电流产生的热量与电阻的关系,因此所选择的两段电阻丝的电阻大小应该不同;
因为煤油的比热容比水的小,相同质量的煤油和水比较,吸收相同的热量,煤油温度升高的多,用煤油做实验效果更明显;
(3)图甲中两电阻丝串联,电流相等,电阻不同,探究的是电热与电阻的关系;
乙装置中一个5Ω的电阻与两个5Ω的电阻并联后再串联,根据串联电路的电流特点可知,右端两个电阻的总电流和左端的电阻电流相等,即I右=I左,两个5Ω的电阻并联,根据并联电路的电流特点知I右=I1+I2,两电阻阻值相等,则支路中电流相等,I1=I2,所以右边容器中的通过电阻的电流是左侧通过电流的一半,因此通电一段时间后,在相同的时间内C瓶煤油比D瓶煤油的温度上升更多,说明在通电时间和电阻相同的情况下,电流越大,电流通过电阻丝产生的热量就越多。
故答案为:(1)相等;温度计示数变化;初温;(2)电流;不相等;比热容;(3)电阻;电流。
10.在“探究电流产生的热量与哪些因素有关”的实验中,实验电路如图1所示,其中R1>R2。
实验一:探究电流产生的热量与电阻大小的关系:
(1)请按照图1中的电路图将图2实物图连接完整;
(2)实验电路按照图1中的电路图连接是为了控制通电时间相同和控制
电流相同 ;电阻丝放出热量的多少,通过
温度计的示数变化 来进行判断。
(3)为了便于比较两根电阻丝通过电流后产生热量的多少,a、b两瓶中要装入
质量 相等、初温相同的同种液体。为了在较短时间内达到明显的实验效果,实验时选用煤油而不选水,是因为煤油的比热容
小于 水的比热容(选填“大于”、“等于”或“小于”)。
实验二:探究电流产生的热量与电流大小的关系:
(4)闭合开关,移动滑动变阻器的滑片,使电路中的电流变成实验一中电流的2倍,且通电时间相同。实验发现:用电阻丝R1加热的煤油,在实验一中温度升高△t1,在实验二中温度升高△t1′,则△t1′ 大于 2△t1(选填“大于”、“等于”或“小于”),该实验说明电流产生的热量与电流大小
不成 正比例关系(选填“成”或“不成”)。实验中,用电阻丝R2加热煤油重复以上实验步骤,也可以得出相同的结论。
(5)如果在两烧瓶中分别装入质量相等的不同液体,并接入两根阻值
相同 的电阻丝(选填“相同”或“不同”),就可用这个装置来探究两种不同液体的吸热性质。假设a烧瓶中液体的质量为m,瓶中电阻丝的阻值为R,测出通过它的电流为I,通电一段时间t后,温度计的示数变化量为△t,若不计热量损失,则a液体的比热容为
c= (用所给出的物理量写出比热容的表达式)。
【解答】解:(1)由电路图可知,滑片左移时变阻器接入电路中的电阻变小,则变阻器左下方接线柱必须接入电路中,如下图所示:
(2)由电路图可知,两电热丝串联在电路中,这是为了控制通电时间相同和控制电流相同;
根据转换法可知,电阻丝放出热量的多少,是通过温度计示数的变化进行比较的;
(3)为了便于比较两根电阻丝通过电流后产生热量的多少,a、b两瓶中要装入质量相等、初温相同的同种液体;
因为煤油的比热容比水的比热容小,相同质量的煤油和水比较,吸收相同的热量,煤油温度升高的多,用煤油做实验效果更明显,便于观察;
(4)闭合开关,移动滑动变阻器的滑片,使电路中的电流变成实验一中电流的2倍,且通电时间相同,
由Q=I2Rt可知,电阻丝产生的热量是原来的4倍,
由Q吸=cm△t的变形式△t=可知,用电阻丝R1加热的煤油,温度升高量△t1′大于2△t1,
该实验说明电流产生的热量与电流不成正比例关系;
(5)实验中两电阻丝串联,通过的电流和通电时间相同,为控制相同时间两液体吸热相同,根据Q=I2Rt可知,选用的两根电阻丝的阻值应相同;
假设a烧瓶中液体的质量为m,瓶中电阻丝的阻值为R,测出通过它的电流为I,通电一段时间t后,电热丝放出的热量Q=I2Rt,
温度计的示数变化量为△t,若不计热量损失,放出的热量全部被液体吸收,由Q吸=cm△t可得,a液体的比热容:c==。
故答案为:(1)如上图所示;(2)电流相同;温度计的示数变化;(3)质量;小于;(4)大于;不成;(4)相同;c=。
11.如图甲所示是小媛家新买的新型电热水壶,该电热水壶有加热、保温和干烧断电功能,其简化电路如图乙所示。S1是壶底温控开关,通常闭合,当壶底发热盘温度达到120℃自动断开,S2是壶壁温控开关,闭合时对水加热,断开时对水保温。已知电热水壶加热功率为1100W,保温功率为55W。求:
(1)电热水壶处于加热状态时,电路中的电流;
(2)电阻R2的阻值;
(3)若水烧开后,S2没有自动断开,当壶里的水烧干瞬间,发热盘的温度为110℃,已知发热盘质量为0.44kg,比热容为0.5×103J/(kg?℃),若水壶的加热效率为80%,则经过多长时间S1才会断开?
【解答】解:
(1)根据P=UI知电热水壶处于加热状态时,电路中的电流为:
I===5A;
(2)由图示和题意可知,当S1、S2闭合时,电路中只有R1工作,电热水壶处于加热状态,
根据P=知R1的阻值为:
R1===44Ω;
当S1闭合,S2断开时,R1与R2串联接入电路,电热水壶处于保温状态,
保温时电路的总电阻为:
R===880Ω,
由串联电路电阻的规律可知电阻R2的阻值为:
R2=R﹣R1=880Ω﹣44Ω=836Ω;
(3)当壶里的水烧干瞬间,发热盘的温度为110℃,当壶底发热盘温度达到120℃时S2自动断开,
该过程中发热盘吸收的热量为:
Q吸=cm(t﹣t0)=0.5×103J/(kg?℃)×0.44kg×(120℃﹣110℃)=2.2×103J,
根据η=得消耗的电能为:
W===2.75×103J,
根据P=得加热时间为:
t===2.5s,
所以当壶里的水烧干瞬间,经过2.5s的时间S1才会断开。
答:(1)电热水壶处于加热状态时,电路中的电流为5A;
(2)电阻R2的阻值为836Ω;
(3)若水烧开后,S2没有自动断开,当壶里的水烧干瞬间,经过2.5s的时间S1才会断开。
12.智能全自动茶炉(如图)内有加热电阻,集抽水、烧水、保温于一体,美观大方,容易操作,如表为某款智能全自动茶炉的部分参数。[ρ水=1.0×103kg/m3,c水=4.2×103J/(kg?℃)]求:
产品名称
智能全自动茶炉
产品型号
XXXX
烧水功率
1210W
容量
0.8L
保温功率
22W
额定电压
220V
(1)将一壶水从20℃加热到70℃,水吸收的热量。
(2)保温状态下通过茶炉的电流。
(3)若用电高峰时,家庭电路的实际电压仅为200V,求该茶炉的实际加热功率(加热电阻阻值不变)。
【解答】解:(1)根据ρ=知水的质量为:
m=ρ水V=1.0×103kg/m3×0.8×10﹣3m3=0.8kg,
水吸热的热量为:
Q吸=c水m(t﹣t0)
=4.2×103J/(kg?℃)×0.8kg×(70℃﹣20℃)
=1.68×105J;
(2)根据P=UI知保温状态下通过茶炉的电流为:
I保温===0.1A;
(3)根据P=知加热电阻为:
R===40Ω,
该茶炉的实际加热功率为:
P实===1000W。
答:(1)将一壶水从20℃加热到70℃,水吸收的热量为1.68×105J;
(2)保温状态下通过茶炉的电流为0.1A;
(3)该茶炉的实际加热功率为1000W。
13.如图所示是某电热器装置的简化电路图,开关S可切换加热和保温两种状态,它的额定电压为220V,额定加热功率是P热=1100W,R1、R2是发热电阻,R2=440Ω。已知电路电压正常,已知水的比热容为4.2×103J/(kg?℃),试完成下列问题:
(1)图中电阻R1的阻值是多大?
(2)该电热器的保温功率P温是多大?
(3)若该电热器将2kg的水从20℃,加热到75℃,需要8min时间,则它加热时将电能转化为水的内能的效率为多少?
【解答】解:(1)当开关S接a时,为R1的简单电路;S接b时,两电阻串联,
因根据串联总电阻大于其中任一电阻,根据P=可知,当开关S接a时,电热器为加热状态;当开关S接b时,电阻R1和R2串联,电热器为保温状态;
由P=可得,电阻R1的阻值:
R1===44Ω;
(2)当开关S接b时,电阻R1和R2串联,为保温状态,
根据P=和电阻的串联知保温功率为:
P保温===100W;
(3)水的初温为20℃,使水的温度升高到75℃,水吸收的热量为:
Q吸=c水m△t=4.2×103J/(kg?℃)×2kg×(75℃﹣20℃)=4.62×105J;
电热器正常工作加热8min消耗的电能:
W=P加热t=1100W×8×60s=5.28×105J;
电热装置的加热效率:
η=×100%×100%=87.5%。
答:(1)图中电阻R1的阻值是44Ω;
(2)该电热器的保温功率P温是100W;
(3)该加热器加热时将电能转化为水的内能的效率为87.5%。
14.多功能养生壶具有精细烹饪、营养量化等功能,深受市场认可和欢迎,如图乙所示是某品牌养生壶简化电路图。
[ρ水=1×103kg/m3,c水=4.2×103J/(kg?℃)]
中温挡功率/W
550
高温挡功率/W
1100
容积/L
1
(1)求R1的阻值。
(2)养生壶在低温挡工作时,求电路中的电流大小。
(3)在标准大气压下,使用高温挡将初温是12℃的一壶水烧开,若养生壶高温挡加热效率为80%,求烧开一壶水需要的时间。
【解答】解:
(1)由图知,当开关S1闭合,S2接B时,电阻R1、R2并联,电路中的总电阻最小,由P=可知,总功率最大,所以此状态为高温挡;
由图知,当开关S1断开,S2接A时,电阻R1、R2串联,电路中的总电阻最大,由P=可知,总功率最小,此时为低温挡;
当S2接A,S1闭合时,R2被短路,只有电阻R1接入电路,养生壶处于中温挡。
由P=UI得,正常工作时通过R1的电流为:I1===2.5A,
由I=得,R1的阻值:R1===88Ω;
(2)因高温挡和中温挡时R1均工作,且两种状态下R1两端电压和电阻均不变,则R1消耗的功率不变,所以高温挡时R2的功率:P2=P高﹣P中=1100W﹣550W=550W,
由P=可知,R2的阻值:R2===88Ω,
由串联电路电阻规律可知,养生壶在低温挡工作时,电路中的电流:I低===1.25A;
(3)由ρ=可得,水的质量:m=ρ水V=1.0×103kg/m3×1×10﹣3m3=1kg,
水吸收的热量:Q吸=c水m△t=4.2×103J/(kg?℃)×1kg×(100℃﹣12℃)=3.696×105J,
由η=可得,养生壶消耗的电能:W===4.62×105J,
由P=可得,烧开一壶水需要的时间:t===420s。
答:(1)R1的阻值为88Ω。
(2)养生壶在低温挡工作时,电路中的电流为1.25A。
(3)烧开一壶水需要的时间为420s。
15.如图是小灵家新购买的电热水器的简化原理图,R1和R2为定值电阻,S为温控开关,a、b是开关的连接触点,电热水器部分参数如表所示。求:
额定电压
220V
加热功率
2000W
保温功率
200W
(1)当把25kg的水由20℃加热到60℃时,水吸收的热量;若热水器加热时的效率为80%,需要消耗的电能。[c水=4.2×103J/(kg?℃)]
(2)R2的阻值。
【解答】解:(1)使水温由20℃升高到60℃,水需要吸收热量为:
Q吸=c水m(t﹣t0)=4.2×103J/(kg?℃)×25kg×(60℃﹣20℃)=4.2×106J;
根据η=得消耗的电能为:
W===5.25×106J;
(2)由电路图可知,开关S与触点a连通时电路为R1的简单电路,开关S与触点b连通时R1与R2串联,
因串联电路中总电阻等于各分电阻之和,
所以,开关S与触点a连通时,电路的总电阻最小,
电源的电压一定,由P=可知,此时电路的总功率最大,热水器处于加热状态;
反之,开关S与触点b连通时,电路的总电阻最大,总功率最小,热水器处于保温状态;
R1的阻值:
R1===24.2Ω,
热水器处于保温状态时,R1与R2串联,此时电路的总电阻:
R===242Ω,
因串联电路中总电阻等于各分电阻之和,
R2的阻值:
R2=R﹣R1=242Ω﹣24.2Ω=217.8Ω。
答:(1)当把25kg的水由20℃加热到60℃时,水吸收的热量为4.2×106J;
若热水器加热时的效率为80%,需要消耗的电能为5.25×106J;
(2)R2的阻值为217.8Ω。
16.甲、乙两个电热器的电阻之比为2:3,通电相同时间产生的热量之比为6:1,则通过甲、乙的电流之比为( )
A.3:1
B.1:3
C.3:2
D.2:3
【解答】解:由题意可知,R甲:R乙=2:3,t甲:t乙=1:1,Q甲:Q乙=6:1,
由Q=I2Rt可得,通过甲、乙的电流之比:
====。
故选:A。
17.甲乙两电热器通过的电流之比为3:2,通电时间之比为2:3,电阻之比为4:3,则产生热量之比为( )
A.1:2
B.2:9
C.2:1
D.9:2
【解答】解:由题意可知,I甲:I乙=3:2,t甲:t乙=2:3,R甲:R乙=4:3,
由Q=I2Rt可得,电流通过甲、乙两个电热器产生的热量之比:
==()2××=()2××=。
故选:C。
18.一阻值为R的电阻丝接在电压为U的电路中,在t时间内放出的热量为Q,现把该电阻丝对折起来接到原来的电路中,放出同样多的热量,需要的时间是( )
A.
B.
C.t
D.2t
【解答】解:导体的电阻与导体的材料、长度,横截面积有关,材料相同时,长度越长,横截面积越小,电阻越大,
该电阻丝对折起来,横截面积变为原来的2倍,长度变为原来的,电阻变为原来的,
根据焦耳定律的变形公式可知原来放出的热量为Q=,
对折起来接到原来的电路中,放出同样多的热量,需要的时间是:t′==t。
故选:A。
19.甲、乙两段导体通电时间相同,甲的电阻是乙的3倍,甲、乙产生的热量之比是4:3,则通过甲、乙两导体的电流之比是( )
A.2:3
B.2:1
C.9:2
D.3:2
【解答】解:由题知,甲、乙两段导体通电时间相同,甲的电阻是乙的3倍,即R甲=3R乙,甲、乙产生的热量之比是4:3,即3Q甲=4Q乙,
由Q=I2Rt有:3I甲2R甲t=4I乙2R乙t,
即:3I甲2×3R乙t=4I乙2R乙t
所以9I甲2=4I乙2,
=。
故选:A。
20.某一阻值为R的电阻,通过的电流为I时,在t时间内产生的热量是Q。则当另一阻值为2R的电阻,通过电流是2I时,在同样的t时间内产生的热量为( )
A.2Q
B.4Q
C.8Q
D.16Q
【解答】解:由题知,阻值为R的电阻,通过的电流为I时,在t时间内产生的热量是Q,
由焦耳定律有:Q=I2Rt,
当另一阻值为2R的电阻,通过电流是2I时,在同样的t时间内产生的热量:
Q'=(2I)2×2R×t=8I2Rt=8Q。
故选:C。
同课章节目录
- 第十三章 内能
- 第1节 分子热运动
- 第2节 内能
- 第3节 比热容
- 第十四章 内能的利用
- 第1节 热机
- 第2节 热机的效率
- 第3节 能量的转化和守恒
- 第十五章 电流和电路
- 第1节 两种电荷
- 第2节 电流和电路
- 第3节 串联和并联
- 第4节 电流的测量
- 第5节 串、并联电路中电流的规律
- 第十六章 电压 电阻
- 第1节 电压
- 第2节 串、并联电路电压的规律
- 第3节 电阻
- 第4节 变阻器
- 第十七章 欧姆定律
- 第1节 电流与电压和电阻的关系
- 第2节 欧姆定律
- 第3节 电阻的测量
- 第4节 欧姆定律在串、并联电路中的应用
- 第十八章 电功率
- 第1节 电能 电功
- 第2节 电功率
- 第3节 测量小灯泡的电功率
- 第4节 焦耳定律
- 第十九章 生活用电
- 第1节 家庭电路
- 第2节 家庭电路电流过大的原因
- 第3节 安全用电
- 第二十章 电与磁
- 第1节 磁现象 磁场
- 第2节 电生磁
- 第3节 电磁铁 电磁继电器
- 第4节 电动机
- 第5节 磁生电
- 第二十一章 信息的传递
- 第1节 现代顺风耳──电话
- 第2节 电磁波的海洋
- 第3节 广播、电视和移动通信
- 第4节 越来越宽的信息之路
- 第二十二章 能源与可持续发展
- 第1节 能源
- 第2节 核能
- 第3节 太阳能
- 第4节 能源与可持续发展
