高二数学《充分条件与必要条件》课件
文档属性
| 名称 | 高二数学《充分条件与必要条件》课件 |  | |
| 格式 | zip | ||
| 文件大小 | 304.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-20 07:50:01 | ||
图片预览








文档简介
(共21张PPT)
二、新课讲授
1、一般地:若p则q为真,记作: 或
若p则q为假,记作:
(1)如果两个三角形全等,那么两三角形面积相等。
(2)“若 则 ”为假命题
例如
两个三角形全等 两三角形面积相等
二、新课讲授
2、充分条件与必要条件
一般地,如果已知 那么我们就说
p是q的充分条件, q是p的必要条件。
两个三形全等 两三角形面积相等。
“两个三形全等”是“两三角形面积相等”的充分条件
“两三角形面积相等”是“两个三形全等 ”的必要条件
例如
3. 充要条件:
(1)若 且 ,则称p是q的充分必要条件,简称充要条件。
说明:①充要条件是互为的;
②“p是q的充要条件”也说成“p与q等价” 、 “p当且仅当q”等.
(2)若 且 ,则称p是q的充分不必要条件。
(3)若 且 ,则称p是q的必要不充分条件。
(4)若 且 ,则称p是q的既不充分也不必要条件。
例题1:说出下列各组命题中,p是q的什么条件?q是p的什么条件?
(1)p: x=y , q: x =y
2
2
2
2
2
2
解:因为: x=y x =y , 且x =y x=y
所以:p是q的充分不必要条件,q是p的必要不充分条件.
即: p q , 而q p
(2) p: (a-2)(a-3)=0, q: a=3
因为:p q , 而q p
所以:p是q的必要不充分条件,q是p的充分不必要条件.
因为: A > B BC > AC . 即:p q
所以:p与q互为充要条件
(3) ABC中,P: A > B . q: BC > AC .
(4)P: a < b . q: <1
a
b
因为: p q 且q p
所以:p是q的既不充分也不必要的条件
q是p的既不充分也不必要的条件
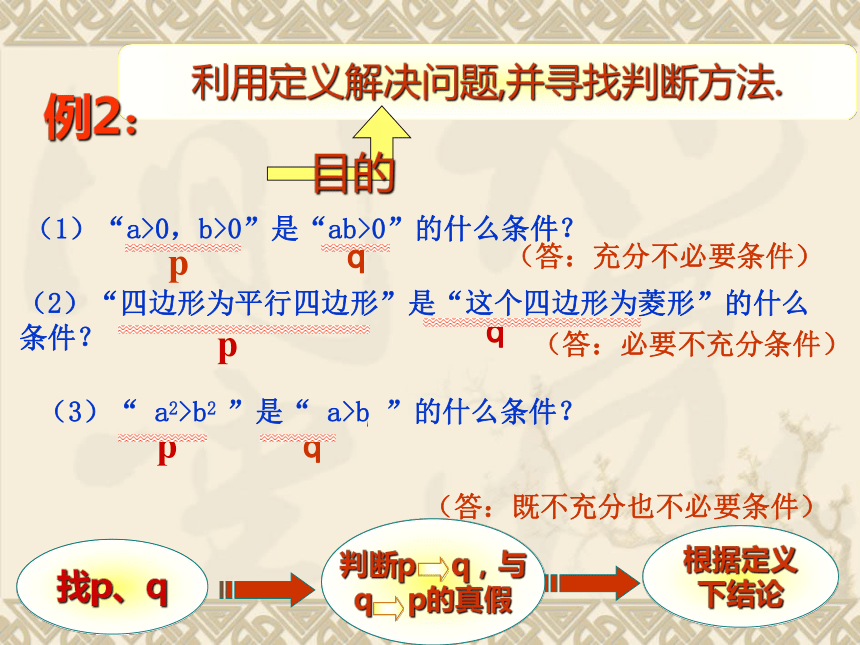
(3)“ a2>b2 ”是“ a>b ”的什么条件?
(2)“四边形为平行四边形”是“这个四边形为菱形”的什么条件?
利用定义解决问题,并寻找判断方法.
目的
p
q
p
p
q
q
找p、q
判断p q,与
q p的真假
根据定义
下结论
(1)“a>0,b>0”是“ab>0”的什么条件?
(答:充分不必要条件)
(答:必要不充分条件)
(答:既不充分也不必要条件)
例2:
例3 下列各题中,那些p是q的充要条件
(1)p: b=0, q: 函数f(x)=ax2+bx+c是偶函数;
(2)P: a>b, q: a+c>b+c.
(1) 是充要条件
(2) 是充要条件
例4 请用“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”填空:
(1)“同位角相等”是“两直线平行”的_________条件.
(2)“x=3”是“x2=9”的______条件.
(3)“四边形的对角线相等”是“四边形为平行四边形”的__________条件.
充分不必要
充要
既不充分也不必要
思考
能否从集合的角度来理解充分条件、必要条件和充要条件?
命题p:“x>3”是命题q:“︱x-2︱>2”的 _____条件
2.命题p:“x=1”是命题q:“x2-3x+2=0”的
_____条件
例5
1.a>b是a>|b|的( )
A.充分而不必要条件
B.必要而不充分条件
C.充要条件
D.既不充分也不必要条件
解析: 由a>b不一定可推出a>|b|,但由a>|b|一定可以推出a>b.
答案: B
2.(2009年天津卷)设x∈R,则“x=1”是“x3=x”的( )
A.充分而不必要条件
B.必要而不充分条件
C.充要条件
D.既不充分也不必要条件
解析: 当x=1时,x3=x成立.
若x3=x,x(x2-1)=0,得x=-1,0,1;不一定得到x=1.
答案: A
3.在“x2+(y-2)2=0是x(y-2)=0的充分不必要条件”这句话中,已知条件是________,结论是________.
答案: x2+(y-2)2=0 x(y-2)=0
[解题过程]
3.试证:一元二次方程ax2+bx+c=0有一正根和一负根的充要条件是ac<0.
所以方程ax2+bx+c=0有两个相异实根,且两根异号.
即方程ax2+bx+c=0有一正根和一负根.
知识小结
1、定义:
(1)若p q,则p是q的充分条件。(p可能会多余浪费)
(2)若q p,则p是q的必要条件(p可能还不足以使q成立)
(3)若p q,则p是q的充要条件。(p不多不少,恰到好处)
2、判别步骤:
(1)找出p、q;
3、判别技巧:
(1)简化命题。 (2)否定命题时举反例。
(3)利用等价的逆否命题来判断。
(3)根据定义下结论。
(2)判断p q与q p的真假。
1.定义法:判断B是A的什么条件,实际上就是判断B A或A B是否成立,只要把题目中所给条件按逻辑关系画出箭头示意图,再利用定义即可判断.
2.转换法:当所给命题的充要条件不易判定时,可对命题进行等价转换,例如改用其逆否命题进行判断.
3.集合法:对命题的条件和结论间的关系进行判断有困难时,有时可以从集合的角度来考虑,记p、q对应的集合分别为A、B,则:
课后作业
二、新课讲授
1、一般地:若p则q为真,记作: 或
若p则q为假,记作:
(1)如果两个三角形全等,那么两三角形面积相等。
(2)“若 则 ”为假命题
例如
两个三角形全等 两三角形面积相等
二、新课讲授
2、充分条件与必要条件
一般地,如果已知 那么我们就说
p是q的充分条件, q是p的必要条件。
两个三形全等 两三角形面积相等。
“两个三形全等”是“两三角形面积相等”的充分条件
“两三角形面积相等”是“两个三形全等 ”的必要条件
例如
3. 充要条件:
(1)若 且 ,则称p是q的充分必要条件,简称充要条件。
说明:①充要条件是互为的;
②“p是q的充要条件”也说成“p与q等价” 、 “p当且仅当q”等.
(2)若 且 ,则称p是q的充分不必要条件。
(3)若 且 ,则称p是q的必要不充分条件。
(4)若 且 ,则称p是q的既不充分也不必要条件。
例题1:说出下列各组命题中,p是q的什么条件?q是p的什么条件?
(1)p: x=y , q: x =y
2
2
2
2
2
2
解:因为: x=y x =y , 且x =y x=y
所以:p是q的充分不必要条件,q是p的必要不充分条件.
即: p q , 而q p
(2) p: (a-2)(a-3)=0, q: a=3
因为:p q , 而q p
所以:p是q的必要不充分条件,q是p的充分不必要条件.
因为: A > B BC > AC . 即:p q
所以:p与q互为充要条件
(3) ABC中,P: A > B . q: BC > AC .
(4)P: a < b . q: <1
a
b
因为: p q 且q p
所以:p是q的既不充分也不必要的条件
q是p的既不充分也不必要的条件
(3)“ a2>b2 ”是“ a>b ”的什么条件?
(2)“四边形为平行四边形”是“这个四边形为菱形”的什么条件?
利用定义解决问题,并寻找判断方法.
目的
p
q
p
p
q
q
找p、q
判断p q,与
q p的真假
根据定义
下结论
(1)“a>0,b>0”是“ab>0”的什么条件?
(答:充分不必要条件)
(答:必要不充分条件)
(答:既不充分也不必要条件)
例2:
例3 下列各题中,那些p是q的充要条件
(1)p: b=0, q: 函数f(x)=ax2+bx+c是偶函数;
(2)P: a>b, q: a+c>b+c.
(1) 是充要条件
(2) 是充要条件
例4 请用“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”填空:
(1)“同位角相等”是“两直线平行”的_________条件.
(2)“x=3”是“x2=9”的______条件.
(3)“四边形的对角线相等”是“四边形为平行四边形”的__________条件.
充分不必要
充要
既不充分也不必要
思考
能否从集合的角度来理解充分条件、必要条件和充要条件?
命题p:“x>3”是命题q:“︱x-2︱>2”的 _____条件
2.命题p:“x=1”是命题q:“x2-3x+2=0”的
_____条件
例5
1.a>b是a>|b|的( )
A.充分而不必要条件
B.必要而不充分条件
C.充要条件
D.既不充分也不必要条件
解析: 由a>b不一定可推出a>|b|,但由a>|b|一定可以推出a>b.
答案: B
2.(2009年天津卷)设x∈R,则“x=1”是“x3=x”的( )
A.充分而不必要条件
B.必要而不充分条件
C.充要条件
D.既不充分也不必要条件
解析: 当x=1时,x3=x成立.
若x3=x,x(x2-1)=0,得x=-1,0,1;不一定得到x=1.
答案: A
3.在“x2+(y-2)2=0是x(y-2)=0的充分不必要条件”这句话中,已知条件是________,结论是________.
答案: x2+(y-2)2=0 x(y-2)=0
[解题过程]
3.试证:一元二次方程ax2+bx+c=0有一正根和一负根的充要条件是ac<0.
所以方程ax2+bx+c=0有两个相异实根,且两根异号.
即方程ax2+bx+c=0有一正根和一负根.
知识小结
1、定义:
(1)若p q,则p是q的充分条件。(p可能会多余浪费)
(2)若q p,则p是q的必要条件(p可能还不足以使q成立)
(3)若p q,则p是q的充要条件。(p不多不少,恰到好处)
2、判别步骤:
(1)找出p、q;
3、判别技巧:
(1)简化命题。 (2)否定命题时举反例。
(3)利用等价的逆否命题来判断。
(3)根据定义下结论。
(2)判断p q与q p的真假。
1.定义法:判断B是A的什么条件,实际上就是判断B A或A B是否成立,只要把题目中所给条件按逻辑关系画出箭头示意图,再利用定义即可判断.
2.转换法:当所给命题的充要条件不易判定时,可对命题进行等价转换,例如改用其逆否命题进行判断.
3.集合法:对命题的条件和结论间的关系进行判断有困难时,有时可以从集合的角度来考虑,记p、q对应的集合分别为A、B,则:
课后作业
