2021-2022学年八年级数学湘教版上册2.5《全等三角形》课时练习(word版含答案)
文档属性
| 名称 | 2021-2022学年八年级数学湘教版上册2.5《全等三角形》课时练习(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 129.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-04 00:00:00 | ||
图片预览

文档简介
湘教版数学八年级上册
2.5《全等三角形》课时练习
一、选择题
1.下列各组中的两个图形属于全等图形的是( )
A.
B.
C.
D.
2.下列说法:
①用一张像底冲洗出来的2张1寸相片是全等形;
②所有的正三角形是全等形;
③全等形的周长相等;
④面积相等的图形一定是全等形.
其中正确的是( )
A.①②③
B.①③④
C.①③
D.③
3.观察如下图所示的各个图形,其中全等图形正确的是( ).
A.②≌④
B.⑤≌⑧
C.①≌⑥
D.③≌⑦
4.如图,在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,那么在下列各条件中,不能判定Rt△ABC≌Rt△A′B′C′的是(
)
A.AB=A′B′=5,BC=B′C′=3
B.AB=B′C′=5,∠A=∠B′=40°
C.AC=A′C′=5,BC=B′C′=3
D.AC=A′C′=5,∠A=∠A′=40°
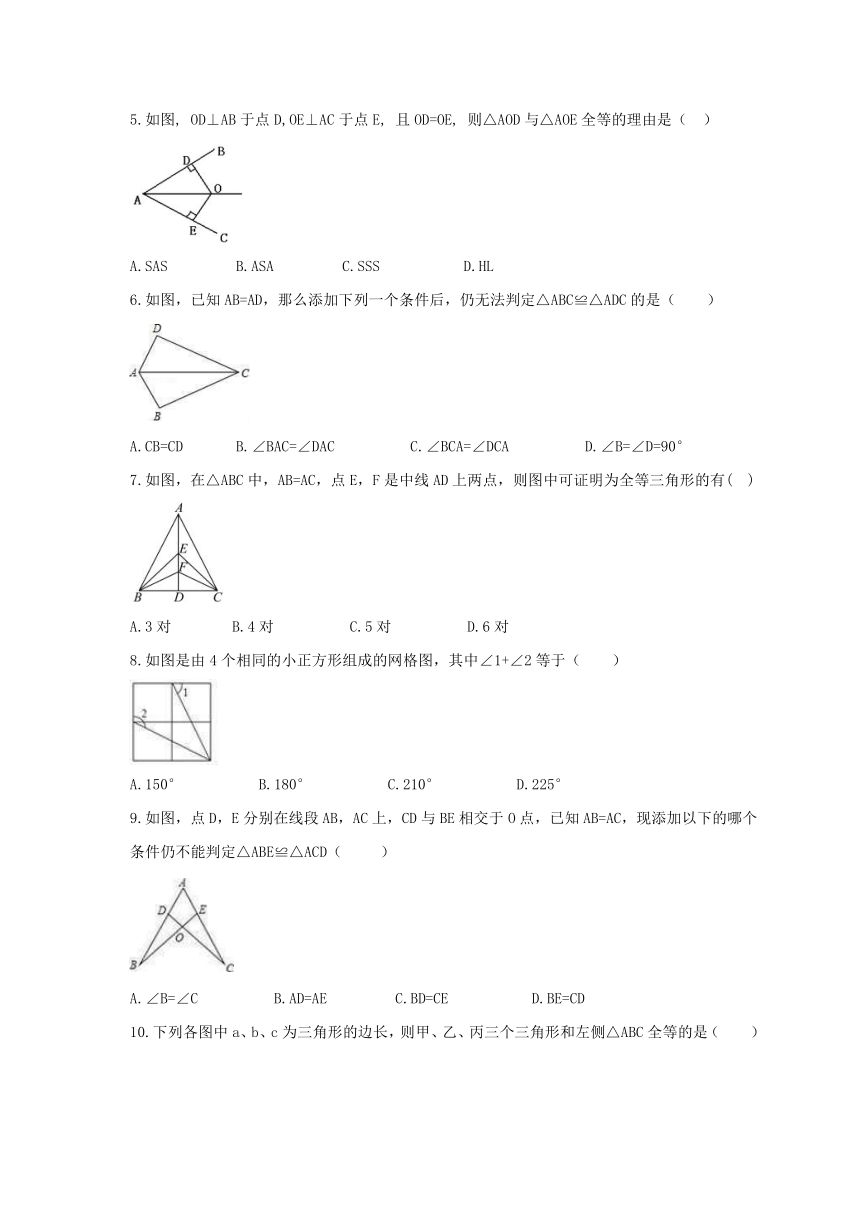
5.如图,
OD⊥AB于点D,OE⊥AC于点E,
且OD=OE,
则△AOD与△AOE全等的理由是(
)
A.SAS
B.ASA
C.SSS
D.HL
6.如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A.CB=CD???
B.∠BAC=∠DAC???
?
C.∠BCA=∠DCA??
??
D.∠B=∠D=90°
7.如图,在△ABC中,AB=AC,点E,F是中线AD上两点,则图中可证明为全等三角形的有(
)
A.3对
B.4对
C.5对
D.6对
8.如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于( )
A.150°?
???
B.180°?
???
C.210°??
??
D.225°
9.如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD(
)
A.∠B=∠C?
???
B.AD=AE????
C.BD=CE?????
D.BE=CD
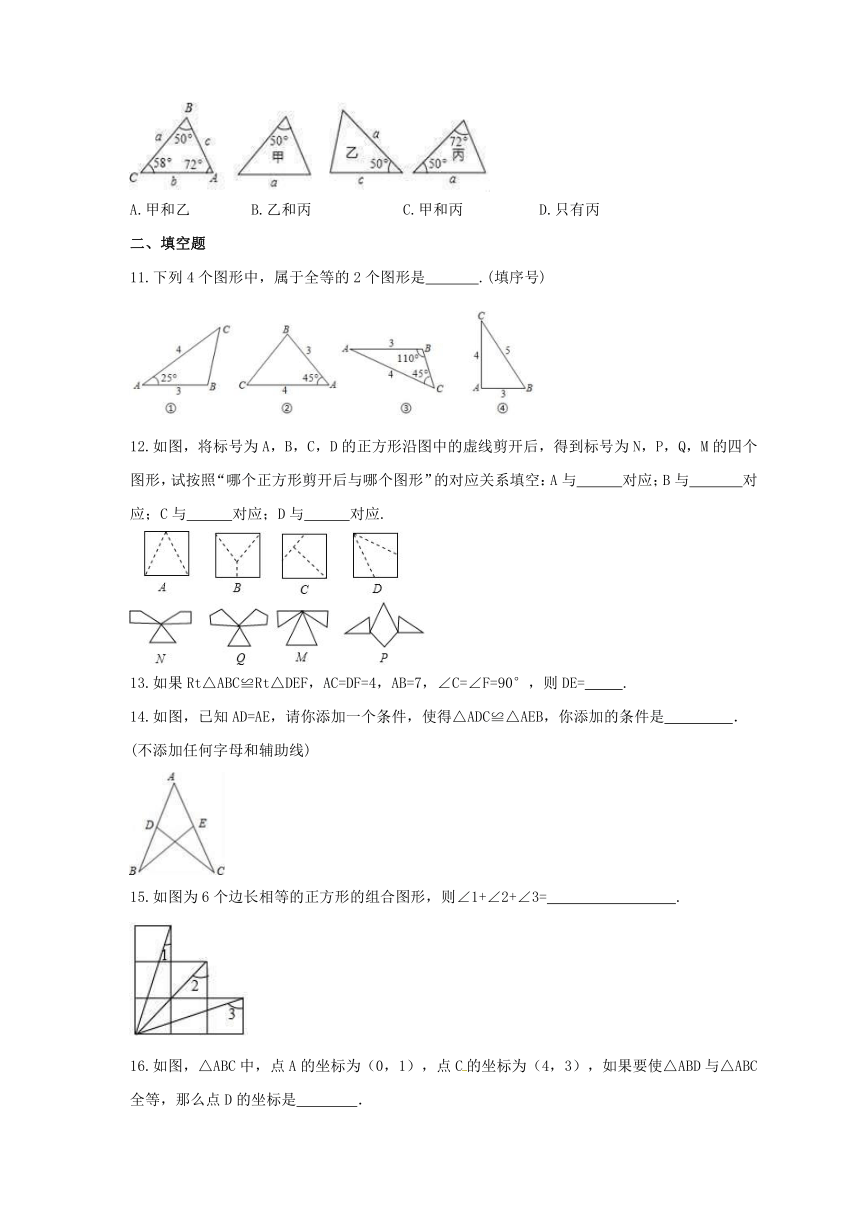
10.下列各图中a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是( )
A.甲和乙??
?
B.乙和丙???
??
C.甲和丙?
???
D.只有丙
二、填空题
11.下列4个图形中,属于全等的2个图形是
.(填序号)
12.如图,将标号为A,B,C,D的正方形沿图中的虚线剪开后,得到标号为N,P,Q,M的四个图形,试按照“哪个正方形剪开后与哪个图形”的对应关系填空:A与
对应;B与
对应;C与
对应;D与
对应.
13.如果Rt△ABC≌Rt△DEF,AC=DF=4,AB=7,∠C=∠F=90°,则DE=
.
14.如图,已知AD=AE,请你添加一个条件,使得△ADC≌△AEB,你添加的条件是 ??
.
(不添加任何字母和辅助线)
15.如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3=????????
.
16.如图,△ABC中,点A的坐标为(0,1),点C的坐标为(4,3),如果要使△ABD与△ABC全等,那么点D的坐标是
.
三、解答题
17.如图,△ABC≌△ADE,BC延长线分别交AD,DE于点F,G,且∠DAC=10°,∠B=∠D=25°,∠EAB=120°.求∠DFB和∠DGB的度数.
18.如图,点O是线段AB的中点,OD∥BC且OD=BC.
(1)求证:△AOD≌△OBC;
(2)若∠ADO=35°,求∠DOC的度数.
19.如图所示,△ADF≌△CBE,且点E,B,D,F在一条直线上.判断AD与BC的位置关系,并加以说明.
20.如图,在△ADF和△BCE中,AF=BE,AC=BD,∠A=∠B,∠B=32°,∠F=28°,BC=5cm,CD=1cm.
求:(1)∠1的度数;(2)AC的长.
参考答案
1.答案为:D.
2.答案为:C.
3.答案为:C
4.答案为:B.
5.答案为:D.
6.答案为:C.
7.答案为:D;
8.答案为:B
9.答案为:D
10.答案为:B
11.答案为:①③.
12.答案为:M,N,Q,P.
13.答案为:7.
14.答案为:AB=AC或∠ADC=∠AEB或∠ABE=∠ACD.
15.答案为:135°.
16.答案为:(4,﹣1)或(﹣1,3)或(﹣1,﹣1)
17.解:∵△ABC≌△ADE,
∴∠BAC=∠DAE.
∵∠EAB=∠BAC+∠DAC+∠DAE,∠DAC=10°,∠EAB=120°,
∴∠BAC=∠DAE=55°,
∴∠BAD=∠CAD+∠BAC=65°.
∵∠DFB是△ABF的一个外角,
∴∠DFB=∠BAF+∠B=65°+25°=90°.
∵∠DFB是△DFG的一个外角,
∴∠DFB=∠D+∠DGB,
∴∠DGB=∠DFB-∠D=90°-25°=65°.
18.
(1)证明:
∵点O是线段AB的中点,∴AO=BO,
∵OD∥BC,∴∠AOD=∠OBC,
在△AOD与△OBC中,,
∴△AOD≌△OBC(SAS);
(2)解:∵△AOD≌△OBC,∴∠ADO=∠OCB=35°,
∵OD∥BC,
∴∠DOC=∠OCB=35°.
9.解:AD与BC的位置关系是:AD∥BC.
理由如下:如图,因为△ADF≌△CBE,
所以∠1=∠2,∠F=∠E.
又点E,B,D,F在一条直线上,
所以∠3=∠1+∠F,∠4=∠2+∠E,
即∠3=∠4.所以AD∥BC.
20.解:(1)∵AC=BD
∴AD=BC且AF=BE,∠A=∠B
∴△ADF≌△BCE(SAS)
∴∠E=∠F=28°,
∴∠1=∠B+∠E=32°+28°=60°;
(2)∵△ADF≌△BCE
∴AD=BC=5cm,且CD=1cm,
∴AC=AD+CD=6cm.
2.5《全等三角形》课时练习
一、选择题
1.下列各组中的两个图形属于全等图形的是( )
A.
B.
C.
D.
2.下列说法:
①用一张像底冲洗出来的2张1寸相片是全等形;
②所有的正三角形是全等形;
③全等形的周长相等;
④面积相等的图形一定是全等形.
其中正确的是( )
A.①②③
B.①③④
C.①③
D.③
3.观察如下图所示的各个图形,其中全等图形正确的是( ).
A.②≌④
B.⑤≌⑧
C.①≌⑥
D.③≌⑦
4.如图,在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,那么在下列各条件中,不能判定Rt△ABC≌Rt△A′B′C′的是(
)
A.AB=A′B′=5,BC=B′C′=3
B.AB=B′C′=5,∠A=∠B′=40°
C.AC=A′C′=5,BC=B′C′=3
D.AC=A′C′=5,∠A=∠A′=40°
5.如图,
OD⊥AB于点D,OE⊥AC于点E,
且OD=OE,
则△AOD与△AOE全等的理由是(
)
A.SAS
B.ASA
C.SSS
D.HL
6.如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A.CB=CD???
B.∠BAC=∠DAC???
?
C.∠BCA=∠DCA??
??
D.∠B=∠D=90°
7.如图,在△ABC中,AB=AC,点E,F是中线AD上两点,则图中可证明为全等三角形的有(
)
A.3对
B.4对
C.5对
D.6对
8.如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于( )
A.150°?
???
B.180°?
???
C.210°??
??
D.225°
9.如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD(
)
A.∠B=∠C?
???
B.AD=AE????
C.BD=CE?????
D.BE=CD
10.下列各图中a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是( )
A.甲和乙??
?
B.乙和丙???
??
C.甲和丙?
???
D.只有丙
二、填空题
11.下列4个图形中,属于全等的2个图形是
.(填序号)
12.如图,将标号为A,B,C,D的正方形沿图中的虚线剪开后,得到标号为N,P,Q,M的四个图形,试按照“哪个正方形剪开后与哪个图形”的对应关系填空:A与
对应;B与
对应;C与
对应;D与
对应.
13.如果Rt△ABC≌Rt△DEF,AC=DF=4,AB=7,∠C=∠F=90°,则DE=
.
14.如图,已知AD=AE,请你添加一个条件,使得△ADC≌△AEB,你添加的条件是 ??
.
(不添加任何字母和辅助线)
15.如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3=????????
.
16.如图,△ABC中,点A的坐标为(0,1),点C的坐标为(4,3),如果要使△ABD与△ABC全等,那么点D的坐标是
.
三、解答题
17.如图,△ABC≌△ADE,BC延长线分别交AD,DE于点F,G,且∠DAC=10°,∠B=∠D=25°,∠EAB=120°.求∠DFB和∠DGB的度数.
18.如图,点O是线段AB的中点,OD∥BC且OD=BC.
(1)求证:△AOD≌△OBC;
(2)若∠ADO=35°,求∠DOC的度数.
19.如图所示,△ADF≌△CBE,且点E,B,D,F在一条直线上.判断AD与BC的位置关系,并加以说明.
20.如图,在△ADF和△BCE中,AF=BE,AC=BD,∠A=∠B,∠B=32°,∠F=28°,BC=5cm,CD=1cm.
求:(1)∠1的度数;(2)AC的长.
参考答案
1.答案为:D.
2.答案为:C.
3.答案为:C
4.答案为:B.
5.答案为:D.
6.答案为:C.
7.答案为:D;
8.答案为:B
9.答案为:D
10.答案为:B
11.答案为:①③.
12.答案为:M,N,Q,P.
13.答案为:7.
14.答案为:AB=AC或∠ADC=∠AEB或∠ABE=∠ACD.
15.答案为:135°.
16.答案为:(4,﹣1)或(﹣1,3)或(﹣1,﹣1)
17.解:∵△ABC≌△ADE,
∴∠BAC=∠DAE.
∵∠EAB=∠BAC+∠DAC+∠DAE,∠DAC=10°,∠EAB=120°,
∴∠BAC=∠DAE=55°,
∴∠BAD=∠CAD+∠BAC=65°.
∵∠DFB是△ABF的一个外角,
∴∠DFB=∠BAF+∠B=65°+25°=90°.
∵∠DFB是△DFG的一个外角,
∴∠DFB=∠D+∠DGB,
∴∠DGB=∠DFB-∠D=90°-25°=65°.
18.
(1)证明:
∵点O是线段AB的中点,∴AO=BO,
∵OD∥BC,∴∠AOD=∠OBC,
在△AOD与△OBC中,,
∴△AOD≌△OBC(SAS);
(2)解:∵△AOD≌△OBC,∴∠ADO=∠OCB=35°,
∵OD∥BC,
∴∠DOC=∠OCB=35°.
9.解:AD与BC的位置关系是:AD∥BC.
理由如下:如图,因为△ADF≌△CBE,
所以∠1=∠2,∠F=∠E.
又点E,B,D,F在一条直线上,
所以∠3=∠1+∠F,∠4=∠2+∠E,
即∠3=∠4.所以AD∥BC.
20.解:(1)∵AC=BD
∴AD=BC且AF=BE,∠A=∠B
∴△ADF≌△BCE(SAS)
∴∠E=∠F=28°,
∴∠1=∠B+∠E=32°+28°=60°;
(2)∵△ADF≌△BCE
∴AD=BC=5cm,且CD=1cm,
∴AC=AD+CD=6cm.
同课章节目录
