2021-2022学年湘教版七年级数学上册第2章 代数式 同步能力达标测评(word解析版)
文档属性
| 名称 | 2021-2022学年湘教版七年级数学上册第2章 代数式 同步能力达标测评(word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 159.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-04 21:39:28 | ||
图片预览




文档简介
2021-2022学年湘教版七年级数学上册《第2章代数式》同步能力达标测评(附答案)
一.选择题(共10小题,每小题3分,共计30分)
1.下列说法正确的是( )
A.2不是单项式
B.是单项式
C.单项式x的系数是0
D.4x2﹣3是多项式
2.若3x2ym与2xm+n﹣1y的和仍为一个单项式,则m2﹣n的值为( )
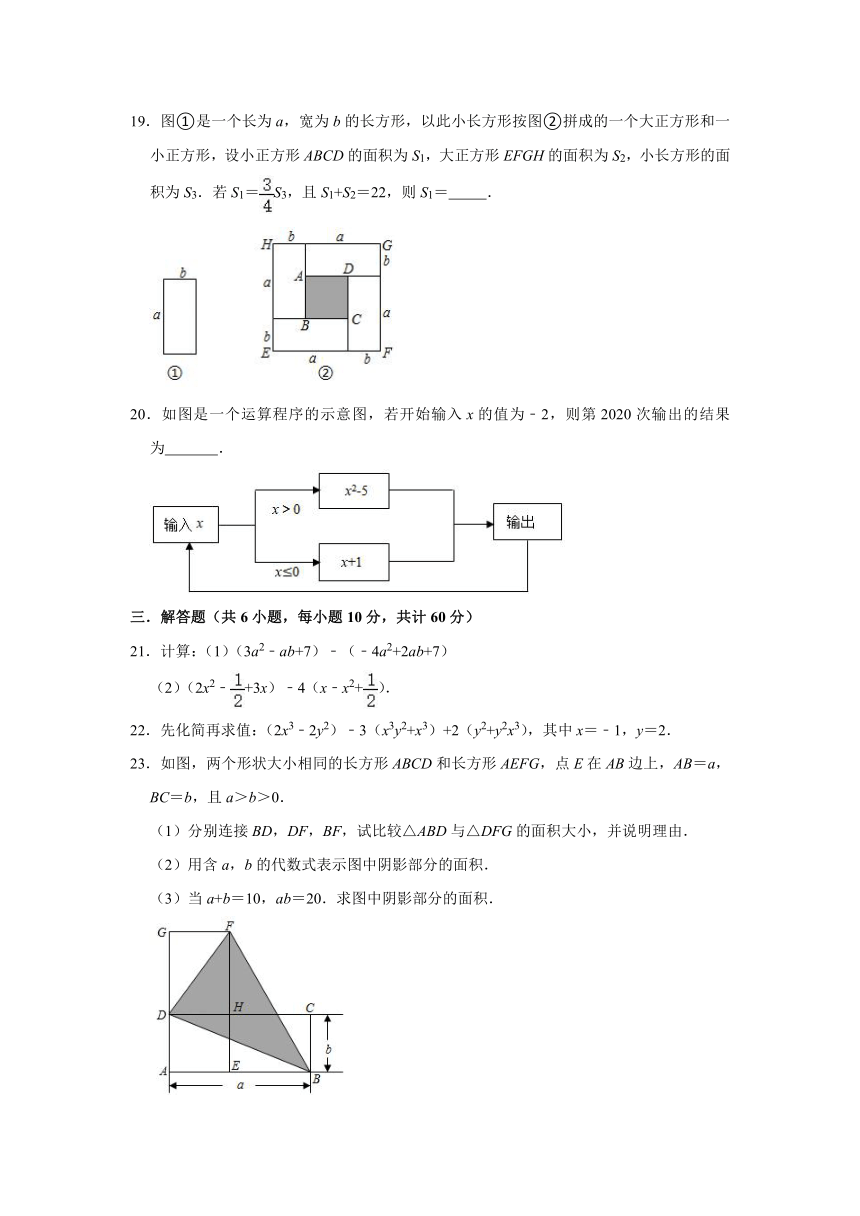
A.1
B.﹣1
C.﹣3
D.3
3.下列计算正确的是( )
A.5x+2y=7xy
B.3x2y﹣4yx2=﹣x2y
C.x2+x5=x7
D.3x﹣2x=1
4.长方形的一边为2a﹣3b,另一边比它小a﹣b,则此长方形的另一边为( )
A.3a﹣4b
B.3a﹣2b
C.a﹣2b
D.a﹣4b
5.已知﹣2xm﹣1y3与xnym+n是同类项,那么(n﹣m)2021的值是( )
A.1
B.﹣1
C.22021
D.0
6.根据图中数字的规律,若第n个图中的q=143,则p的值为( )
A.100
B.121
C.144
D.169
7.将从1开始的连续奇数按如图所示的规律排列,例如,位于第4行第3列的数为27,则位于第32行第13列的数是( )
A.2025
B.2023
C.2021
D.2019
8.某地居民生活用水收费标准:每月用水量不超过17立方米,每立方米a元;超过部分每立方米(a+1.2)元.该地区某用户上月用水量为20立方米,则应缴水费为( )
A.20a元
B.(20a+24)元
C.(17a+3.6)元
D.(20a+3.6)元
9.某超市出售一商品,有如下四种在原标价基础上调价的方案,其中调价后售价最低的是( )
A.先打九五折,再打九五折
B.先提价50%,再打六折
C.先提价30%,再降价30%
D.先提价25%,再降价25%
10.求1+2+22+23+…+22021的值,可令S=1+2+22+23+…+22021,则2S=2+22+23+24+…+22022,因此2S﹣S=22022﹣1.仿照以上推理,计算出1+5+52+53+…+52021的值为( )
A.52021﹣1
B.52022﹣1
C.
D.
二.填空题(共10小题,每小题3分,共计30分)
11.若单项式3xm﹣1y2与单项式x3yn+1是同类项,则m﹣n=
.
12.已知a2+a=0,则2a2+2a+2021=
.
13.如图(图中长度单位:米),用含x的式子表示阴影部分的面积是
平方米.
14.当x=2时,代数式ax3﹣bx+1的值等于﹣17,那么当x=﹣1时,代数式﹣3bx3+12ax﹣5的值
.
15.如图,用火柴棒按如图所示的方式搭一行三角形,搭1个三角形需3枝火柴棒,搭2个三角形需5枝火柴棒,搭3个三角形需7枝火柴棒,照这样的规律搭下去,搭2020个三角形需要火柴棒
枝.
16.已知(x+1)2021=a0+a1x1+a2x2+a3x3+…+a2021x2021,则a2021﹣a2020+a2019﹣a2018+…+a1的值为
.
17.观察下列等式:1=12﹣02,3=22﹣12,5=32﹣22,…按此规律,则第n个等式为2n﹣1=
.
18.已知整数a1,a2,…,an(n为正整数)满足a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,…,以此类推,则a2021=
.
19.图①是一个长为a,宽为b的长方形,以此小长方形按图②拼成的一个大正方形和一小正方形,设小正方形ABCD的面积为S1,大正方形EFGH的面积为S2,小长方形的面积为S3.若S1=S3,且S1+S2=22,则S1=
.
20.如图是一个运算程序的示意图,若开始输入x的值为﹣2,则第2020次输出的结果为
.
三.解答题(共6小题,每小题10分,共计60分)
21.计算:(1)(3a2﹣ab+7)﹣(﹣4a2+2ab+7)
(2)(2x2﹣+3x)﹣4(x﹣x2+).
22.先化简再求值:(2x3﹣2y2)﹣3(x3y2+x3)+2(y2+y2x3),其中x=﹣1,y=2.
23.如图,两个形状大小相同的长方形ABCD和长方形AEFG,点E在AB边上,AB=a,BC=b,且a>b>0.
(1)分别连接BD,DF,BF,试比较△ABD与△DFG的面积大小,并说明理由.
(2)用含a,b的代数式表示图中阴影部分的面积.
(3)当a+b=10,ab=20.求图中阴影部分的面积.
24.(1)先化简再求值(ab+3a2)﹣2(a2﹣2ab),其中|a﹣1|+(b+2)2=0.
(2)已知:A=x3+2x+3,B=2x3﹣xy+2.
①求2A﹣B;
②若2A﹣B的值与x无关,求y的值.
25.将正整数按一定的规律排成下图所示的10列,规定从上到下依次为1行、2行、3行…,从左到右依次为第1列至第10列.
(1)数2019在第几行,第几列?
(2)把图中带阴影的3个方格当作一个整体平移,设被框住的3个数中,最大的一个数为x.则被框住的三个数的和能否等于2020?若能,求出x的值;若不能,请说明理由.
26.我省教育厅发布文件,规定从2021年开始,体育成绩将按一定的原始分计入中考总分.某校为适应新的中考要求,决定为体育组添置一批体育器材.学校准备订购一批篮球和跳绳,经过市场调查后发现篮球每个定价120元,跳绳每条定价20元.某体育用品商店提供A、B两种优惠方案:
A方案:买一个篮球送一条跳绳;
B方案:篮球和跳绳都按定价的90%付款.
已知要购买篮球50个,跳绳x条(x>50).
(1)若按A方案购买,一共需付款
元;(用含x的代数式表示)若按B方案购买,一共需付款
元.(用含x的代数式表示)
(2)当x=100时,请通过计算说明此时用哪种方案购买较为合算?
(3)当x=100时,你能给出一种更为省钱的购买方案吗?请写出你的购买方案,并计算需付款多少元?
参考答案
一.选择题(共10小题,每小题3分,共计30分)
1.解:A.2是单项式,故此选项不合题意;
B.不是单项式,故此选项不合题意;
C.单项式x的系数是1,故此选项不合题意;
D.4x2﹣3是多项式,故此选项符合题意.
故选:D.
2.解:由题意知3x2ym与2xm+n﹣1y是同类项,
所以有m+n﹣1=2,m=1,
即n=2,m=1,
m2﹣n=12﹣2=﹣1,
故选:B.
3.解:A选项,5x和2y不是同类项,不能合并,故该选项计算错误;
B选项,原式=3x2y﹣4x2y=﹣x2y,故该选项计算正确;
C选项,x2和x5不是同类项,不能合并,故该选项计算错误;
D选项,3x﹣2x=x,故该选项计算错误;
故选:B.
4.解:∵长方形的一边为2a﹣3b,另一边比它小a﹣b,
∴此长方形的另一边为:2a﹣3b﹣(a﹣b)=2a﹣3b﹣a+b=a﹣2b.
故选:C.
5.解:由题意得:,
解得:,
则(n﹣m)2021=(1﹣2)2021=﹣1,
故选:B.
6.解:通过观察可得规律:p=n2,q=(n+1)2﹣1,
∵q=143,
∴(n+1)2﹣1=143,
解得:n=11,
∴p=n2=112=121,
故选:B.
7.解:由题意可知:
行数为1的方阵内包含“1”,共1个数;
行数为2的方阵内包含“1、3、5、7”,共22个数;
行数为3的方阵内包含“1、3、5、7、9、11、13、15、17”,共32个数;
∴行数为32的方阵内包含“1、3、5、7、......”共322个数,即共1024个数,
∴位于第32行第13列的数是连续奇数的第(1024﹣12)═1012个数,
∴位于第32行第13列的数是:2×1012﹣1═2023.
故选:B.
8.解:根据题意知:17a+(20﹣17)(a+1.2)=(20a+3.6)(元)。
故选:D.
9.解:设商品原标价为a元,
A.先打九五折,再打九五折的售价为:0.95×0.95a=0.9025a(元);
B.先提价50%,再打六折的售价为:(1+50%)×0.6a=0.9a(元);
C.先提价30%,再降价30%的售价为:(1+30%)(1﹣30%)a=0.91a(元);
D.先提价25%,再降价25%的售价为:(1+25%)(1﹣25%)a=0.9375a(元);
∵0.9a<0.9025a<0.91a<0.9375a,
∴B选项的调价方案调价后售价最低,
故选:B.
10.解:根据题目给出的方法,
令T=1+5+52+53+…+52021,
则5T=5+52+53+…+52022,
∴5T﹣T=52022﹣1,
∴T=,
故选:C.
二.填空题(共10小题,每小题3分,共计30分)
11.解:∵单项式3xm﹣1y2与单项式x3yn+1是同类项,
∴m﹣1=3,n+1=2,
解得m=4,n=1,
∴m﹣n=4﹣1=3.
故答案为:3.
12.解:∵a2+a=0,
∴2a2+2a+2021
=2(a2+a)+2021
=2×0+2021
=0+2021
=2021.
故答案为:2021.
13.解:阴影部分的面积=x2+3x+2×3=(x2+3x+6)平方米.
故答案是:(x2+3x+6).
14.解:x=2时,ax3﹣bx+1=a?23﹣b?2+1=8a﹣2b+1,
∴8a﹣2b+1=﹣17,
∴8a﹣2b=﹣18,
∴4a﹣b=﹣9.
当x=﹣1时,﹣3bx31+2ax﹣5=12a×(﹣1)﹣3b×(﹣1)3﹣5,
=﹣12a+3b﹣5
=﹣3(4a﹣b)﹣5
=﹣3×(﹣9)﹣5
=27﹣5
=22.
故答案为:22.
15.解:第一个三角形需要3枝火柴棒;
第二个三角形需要(3+2)枝火柴棒;
第3个三角形需要(3+2×2)枝火柴棒.
…
第n个三角形需要[3+(n﹣1)×2]=2n+1枝火柴棒.
所以,第2020个三角形需要火柴棒=2×2020+1=4041(枝).
故答案为:4041.
16.解:令x=0,则(x+1)2021=a0=1,
令x=﹣1,则(x+1)2021=a0﹣a1+a2﹣a3+...+a2020﹣a2021=0,
即(a0﹣a1)+(a2﹣a3)+...+(a2020﹣a2021)=0,
等式两边同乘﹣1,得(a1﹣a0)+(a3﹣a2)+...+(a2021﹣a2020)=0,
运用加法交换律,得(a2021﹣a2020)+(a2019﹣a2018)+...+(a1﹣a0)=0,
即
a2021﹣a2020+a2019﹣a2018+...+a1﹣a0=0,
∴a2021﹣a2020+a2019﹣a2018+...+a1=a0=1,
故答案为1.
17.解:∵1=12﹣02,3=22﹣12,5=32﹣22,…,
∴第n个等式为2n﹣1=n2﹣(n﹣1)2,
故答案为:n2﹣(n﹣1)2.
18.解:由题知a1=0,
a2=﹣|a1+1|=﹣1,
a3=﹣|a2+2|=﹣1,
a4=﹣|a3+3|=﹣2,
a5=﹣|a4+4|=﹣2,
a6=﹣|a5+5|=﹣3,
…,
所以n是奇数时,an=﹣,
n是偶数时,an=﹣,
∴a2021=﹣1010,
故答案为:﹣1010.
19.解:由图可得:大正方形EFGH的面积=小正方形ABCD的面积+4×小长方形的面积,即S2=S1+4S3,
∵S1=S3,
∴S3=S1,
∵S1+S2=22,
∴S2=22﹣S1,
∴22﹣S1=S1+4×S1,
解得S1=3.
故答案为:3.
20.解:第一次输入:∵x=﹣2<0,
∴x+1=﹣2+1=﹣1,
第二次输入:∵﹣1<0,
∴x+1=﹣1+1=0;
第三次输入:∴x+1=0+1=1,
第四次输入:∵1>0,
∴x2﹣5=12﹣5=﹣4,
第五次输入:∵﹣4≤0,
∴x+1=﹣4+1=﹣3,
第六次输入:∵﹣3<0,
∴x+1=﹣3+1=﹣2,
第七次输入:∵﹣2<0,
∴x+1=﹣2+1=﹣1,
……
依此类推,
2020÷6=336…4,
所以输出的结果是﹣4,
故答案为:﹣4.
三.解答题(共6小题,每小题10分,共计60分)
21.解:(1)(3a2﹣ab+7)﹣(﹣4a2+2ab+7)
=3a2﹣ab+7+4a2﹣2ab﹣7
=7a2﹣3ab;
(2)(2x2﹣+3x)﹣4(x﹣x2+)
=2x2﹣+3x﹣4x+4x2﹣2
=6x2﹣x﹣2.5.
22.解:(2x3﹣2y2)﹣3(x3y2+x3)+2(y2+y2x3)
=2x3﹣2y2﹣3x3y2﹣3x3+2y2+2x3y2
=﹣x3﹣x3y2.
当x=﹣1,y=2时,
原式=﹣(﹣1)3﹣(﹣1)3×22
=1+4
=5.
23.解:(1)S△ABD>S△DFG,理由如下:
∵S△ABD=AB?AD=ab,
S△DFG=DG?FG=(a﹣b)?b=ab﹣b2<ab,
∵a>b>0,
∴S△ABD>S△DFG.
(2)如图,延长BC,GF交于I,
S阴影=S?ABIG﹣S△ABD﹣S△DFG﹣S△BIF,
∴S阴影=a2﹣ab﹣?b?(a﹣b)﹣?a?(a﹣b)=a2+b2﹣ab;
∴阴影部分的面积用代数式表示为:a2+b2﹣ab;
(3)当a+b=10,ab=20时,a2+b2﹣ab=(a+b)2﹣ab=×102﹣×20=20.
24.解:(1)(ab+3a2)﹣2(a2﹣2ab)
=ab+3a2﹣2a2+4ab
=a2+5ab,
∵|a﹣1|+(b+2)2=0.
∴a=1,b=﹣2,
∴原式=12+5×1×(﹣2)
=1﹣10
=﹣9;
(2)①2A﹣B
=2(x3+2x+3)﹣(2x3﹣xy+2)
=2x3+4x+6﹣2x3+xy﹣2
=xy+4x+4;
②若2A﹣B的值与x无关,则y+4=0,
∴y=﹣4.
25.解:(1)表格每行有10个数字,
2019÷10=201???9,201+1=202,
∴2019在第202行,第9列.
(2)∵被框住的3个数中,最大的一个数为x,
∴另外两个数为x﹣11和x﹣9,
∴x﹣11+x﹣9+x=2020,
解得x=680,680﹣11=669,680﹣9=671,
∵680在第68行第10列,671在67行第1列,
∴被框住的三个数的和不能等于2020.
26.解:(1)A方案购买可列式:50×120+(x﹣50)×20=5000+20x(元);
按B方案购买可列式:(50×120+20x)×0.9=5400+18x(元);
故答案为:(5000+20x),(5400+18x);
(2)当x=100时,
A方案购买需付款:5000+20x=5000+20×100=7000(元);
按B方案购买需付款:5400+18x=5400+18×100=7200(元);
∵7000<7200,
∴当x=100时,应选择A方案购买合算;
(3)由(2)可知,当x=100时,A方案付款7000元,B方案付款7200元,
按A方案购买50个篮球配送50个跳绳,按B方案购买50个跳绳合计需付款:
120×50+20×50×90%=6900,
∵6900<7000<7200,
∴省钱的购买方案是:
按A方案买50个篮球,剩下的50条跳绳按B方案购买,付款6900元.
一.选择题(共10小题,每小题3分,共计30分)
1.下列说法正确的是( )
A.2不是单项式
B.是单项式
C.单项式x的系数是0
D.4x2﹣3是多项式
2.若3x2ym与2xm+n﹣1y的和仍为一个单项式,则m2﹣n的值为( )
A.1
B.﹣1
C.﹣3
D.3
3.下列计算正确的是( )
A.5x+2y=7xy
B.3x2y﹣4yx2=﹣x2y
C.x2+x5=x7
D.3x﹣2x=1
4.长方形的一边为2a﹣3b,另一边比它小a﹣b,则此长方形的另一边为( )
A.3a﹣4b
B.3a﹣2b
C.a﹣2b
D.a﹣4b
5.已知﹣2xm﹣1y3与xnym+n是同类项,那么(n﹣m)2021的值是( )
A.1
B.﹣1
C.22021
D.0
6.根据图中数字的规律,若第n个图中的q=143,则p的值为( )
A.100
B.121
C.144
D.169
7.将从1开始的连续奇数按如图所示的规律排列,例如,位于第4行第3列的数为27,则位于第32行第13列的数是( )
A.2025
B.2023
C.2021
D.2019
8.某地居民生活用水收费标准:每月用水量不超过17立方米,每立方米a元;超过部分每立方米(a+1.2)元.该地区某用户上月用水量为20立方米,则应缴水费为( )
A.20a元
B.(20a+24)元
C.(17a+3.6)元
D.(20a+3.6)元
9.某超市出售一商品,有如下四种在原标价基础上调价的方案,其中调价后售价最低的是( )
A.先打九五折,再打九五折
B.先提价50%,再打六折
C.先提价30%,再降价30%
D.先提价25%,再降价25%
10.求1+2+22+23+…+22021的值,可令S=1+2+22+23+…+22021,则2S=2+22+23+24+…+22022,因此2S﹣S=22022﹣1.仿照以上推理,计算出1+5+52+53+…+52021的值为( )
A.52021﹣1
B.52022﹣1
C.
D.
二.填空题(共10小题,每小题3分,共计30分)
11.若单项式3xm﹣1y2与单项式x3yn+1是同类项,则m﹣n=
.
12.已知a2+a=0,则2a2+2a+2021=
.
13.如图(图中长度单位:米),用含x的式子表示阴影部分的面积是
平方米.
14.当x=2时,代数式ax3﹣bx+1的值等于﹣17,那么当x=﹣1时,代数式﹣3bx3+12ax﹣5的值
.
15.如图,用火柴棒按如图所示的方式搭一行三角形,搭1个三角形需3枝火柴棒,搭2个三角形需5枝火柴棒,搭3个三角形需7枝火柴棒,照这样的规律搭下去,搭2020个三角形需要火柴棒
枝.
16.已知(x+1)2021=a0+a1x1+a2x2+a3x3+…+a2021x2021,则a2021﹣a2020+a2019﹣a2018+…+a1的值为
.
17.观察下列等式:1=12﹣02,3=22﹣12,5=32﹣22,…按此规律,则第n个等式为2n﹣1=
.
18.已知整数a1,a2,…,an(n为正整数)满足a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,…,以此类推,则a2021=
.
19.图①是一个长为a,宽为b的长方形,以此小长方形按图②拼成的一个大正方形和一小正方形,设小正方形ABCD的面积为S1,大正方形EFGH的面积为S2,小长方形的面积为S3.若S1=S3,且S1+S2=22,则S1=
.
20.如图是一个运算程序的示意图,若开始输入x的值为﹣2,则第2020次输出的结果为
.
三.解答题(共6小题,每小题10分,共计60分)
21.计算:(1)(3a2﹣ab+7)﹣(﹣4a2+2ab+7)
(2)(2x2﹣+3x)﹣4(x﹣x2+).
22.先化简再求值:(2x3﹣2y2)﹣3(x3y2+x3)+2(y2+y2x3),其中x=﹣1,y=2.
23.如图,两个形状大小相同的长方形ABCD和长方形AEFG,点E在AB边上,AB=a,BC=b,且a>b>0.
(1)分别连接BD,DF,BF,试比较△ABD与△DFG的面积大小,并说明理由.
(2)用含a,b的代数式表示图中阴影部分的面积.
(3)当a+b=10,ab=20.求图中阴影部分的面积.
24.(1)先化简再求值(ab+3a2)﹣2(a2﹣2ab),其中|a﹣1|+(b+2)2=0.
(2)已知:A=x3+2x+3,B=2x3﹣xy+2.
①求2A﹣B;
②若2A﹣B的值与x无关,求y的值.
25.将正整数按一定的规律排成下图所示的10列,规定从上到下依次为1行、2行、3行…,从左到右依次为第1列至第10列.
(1)数2019在第几行,第几列?
(2)把图中带阴影的3个方格当作一个整体平移,设被框住的3个数中,最大的一个数为x.则被框住的三个数的和能否等于2020?若能,求出x的值;若不能,请说明理由.
26.我省教育厅发布文件,规定从2021年开始,体育成绩将按一定的原始分计入中考总分.某校为适应新的中考要求,决定为体育组添置一批体育器材.学校准备订购一批篮球和跳绳,经过市场调查后发现篮球每个定价120元,跳绳每条定价20元.某体育用品商店提供A、B两种优惠方案:
A方案:买一个篮球送一条跳绳;
B方案:篮球和跳绳都按定价的90%付款.
已知要购买篮球50个,跳绳x条(x>50).
(1)若按A方案购买,一共需付款
元;(用含x的代数式表示)若按B方案购买,一共需付款
元.(用含x的代数式表示)
(2)当x=100时,请通过计算说明此时用哪种方案购买较为合算?
(3)当x=100时,你能给出一种更为省钱的购买方案吗?请写出你的购买方案,并计算需付款多少元?
参考答案
一.选择题(共10小题,每小题3分,共计30分)
1.解:A.2是单项式,故此选项不合题意;
B.不是单项式,故此选项不合题意;
C.单项式x的系数是1,故此选项不合题意;
D.4x2﹣3是多项式,故此选项符合题意.
故选:D.
2.解:由题意知3x2ym与2xm+n﹣1y是同类项,
所以有m+n﹣1=2,m=1,
即n=2,m=1,
m2﹣n=12﹣2=﹣1,
故选:B.
3.解:A选项,5x和2y不是同类项,不能合并,故该选项计算错误;
B选项,原式=3x2y﹣4x2y=﹣x2y,故该选项计算正确;
C选项,x2和x5不是同类项,不能合并,故该选项计算错误;
D选项,3x﹣2x=x,故该选项计算错误;
故选:B.
4.解:∵长方形的一边为2a﹣3b,另一边比它小a﹣b,
∴此长方形的另一边为:2a﹣3b﹣(a﹣b)=2a﹣3b﹣a+b=a﹣2b.
故选:C.
5.解:由题意得:,
解得:,
则(n﹣m)2021=(1﹣2)2021=﹣1,
故选:B.
6.解:通过观察可得规律:p=n2,q=(n+1)2﹣1,
∵q=143,
∴(n+1)2﹣1=143,
解得:n=11,
∴p=n2=112=121,
故选:B.
7.解:由题意可知:
行数为1的方阵内包含“1”,共1个数;
行数为2的方阵内包含“1、3、5、7”,共22个数;
行数为3的方阵内包含“1、3、5、7、9、11、13、15、17”,共32个数;
∴行数为32的方阵内包含“1、3、5、7、......”共322个数,即共1024个数,
∴位于第32行第13列的数是连续奇数的第(1024﹣12)═1012个数,
∴位于第32行第13列的数是:2×1012﹣1═2023.
故选:B.
8.解:根据题意知:17a+(20﹣17)(a+1.2)=(20a+3.6)(元)。
故选:D.
9.解:设商品原标价为a元,
A.先打九五折,再打九五折的售价为:0.95×0.95a=0.9025a(元);
B.先提价50%,再打六折的售价为:(1+50%)×0.6a=0.9a(元);
C.先提价30%,再降价30%的售价为:(1+30%)(1﹣30%)a=0.91a(元);
D.先提价25%,再降价25%的售价为:(1+25%)(1﹣25%)a=0.9375a(元);
∵0.9a<0.9025a<0.91a<0.9375a,
∴B选项的调价方案调价后售价最低,
故选:B.
10.解:根据题目给出的方法,
令T=1+5+52+53+…+52021,
则5T=5+52+53+…+52022,
∴5T﹣T=52022﹣1,
∴T=,
故选:C.
二.填空题(共10小题,每小题3分,共计30分)
11.解:∵单项式3xm﹣1y2与单项式x3yn+1是同类项,
∴m﹣1=3,n+1=2,
解得m=4,n=1,
∴m﹣n=4﹣1=3.
故答案为:3.
12.解:∵a2+a=0,
∴2a2+2a+2021
=2(a2+a)+2021
=2×0+2021
=0+2021
=2021.
故答案为:2021.
13.解:阴影部分的面积=x2+3x+2×3=(x2+3x+6)平方米.
故答案是:(x2+3x+6).
14.解:x=2时,ax3﹣bx+1=a?23﹣b?2+1=8a﹣2b+1,
∴8a﹣2b+1=﹣17,
∴8a﹣2b=﹣18,
∴4a﹣b=﹣9.
当x=﹣1时,﹣3bx31+2ax﹣5=12a×(﹣1)﹣3b×(﹣1)3﹣5,
=﹣12a+3b﹣5
=﹣3(4a﹣b)﹣5
=﹣3×(﹣9)﹣5
=27﹣5
=22.
故答案为:22.
15.解:第一个三角形需要3枝火柴棒;
第二个三角形需要(3+2)枝火柴棒;
第3个三角形需要(3+2×2)枝火柴棒.
…
第n个三角形需要[3+(n﹣1)×2]=2n+1枝火柴棒.
所以,第2020个三角形需要火柴棒=2×2020+1=4041(枝).
故答案为:4041.
16.解:令x=0,则(x+1)2021=a0=1,
令x=﹣1,则(x+1)2021=a0﹣a1+a2﹣a3+...+a2020﹣a2021=0,
即(a0﹣a1)+(a2﹣a3)+...+(a2020﹣a2021)=0,
等式两边同乘﹣1,得(a1﹣a0)+(a3﹣a2)+...+(a2021﹣a2020)=0,
运用加法交换律,得(a2021﹣a2020)+(a2019﹣a2018)+...+(a1﹣a0)=0,
即
a2021﹣a2020+a2019﹣a2018+...+a1﹣a0=0,
∴a2021﹣a2020+a2019﹣a2018+...+a1=a0=1,
故答案为1.
17.解:∵1=12﹣02,3=22﹣12,5=32﹣22,…,
∴第n个等式为2n﹣1=n2﹣(n﹣1)2,
故答案为:n2﹣(n﹣1)2.
18.解:由题知a1=0,
a2=﹣|a1+1|=﹣1,
a3=﹣|a2+2|=﹣1,
a4=﹣|a3+3|=﹣2,
a5=﹣|a4+4|=﹣2,
a6=﹣|a5+5|=﹣3,
…,
所以n是奇数时,an=﹣,
n是偶数时,an=﹣,
∴a2021=﹣1010,
故答案为:﹣1010.
19.解:由图可得:大正方形EFGH的面积=小正方形ABCD的面积+4×小长方形的面积,即S2=S1+4S3,
∵S1=S3,
∴S3=S1,
∵S1+S2=22,
∴S2=22﹣S1,
∴22﹣S1=S1+4×S1,
解得S1=3.
故答案为:3.
20.解:第一次输入:∵x=﹣2<0,
∴x+1=﹣2+1=﹣1,
第二次输入:∵﹣1<0,
∴x+1=﹣1+1=0;
第三次输入:∴x+1=0+1=1,
第四次输入:∵1>0,
∴x2﹣5=12﹣5=﹣4,
第五次输入:∵﹣4≤0,
∴x+1=﹣4+1=﹣3,
第六次输入:∵﹣3<0,
∴x+1=﹣3+1=﹣2,
第七次输入:∵﹣2<0,
∴x+1=﹣2+1=﹣1,
……
依此类推,
2020÷6=336…4,
所以输出的结果是﹣4,
故答案为:﹣4.
三.解答题(共6小题,每小题10分,共计60分)
21.解:(1)(3a2﹣ab+7)﹣(﹣4a2+2ab+7)
=3a2﹣ab+7+4a2﹣2ab﹣7
=7a2﹣3ab;
(2)(2x2﹣+3x)﹣4(x﹣x2+)
=2x2﹣+3x﹣4x+4x2﹣2
=6x2﹣x﹣2.5.
22.解:(2x3﹣2y2)﹣3(x3y2+x3)+2(y2+y2x3)
=2x3﹣2y2﹣3x3y2﹣3x3+2y2+2x3y2
=﹣x3﹣x3y2.
当x=﹣1,y=2时,
原式=﹣(﹣1)3﹣(﹣1)3×22
=1+4
=5.
23.解:(1)S△ABD>S△DFG,理由如下:
∵S△ABD=AB?AD=ab,
S△DFG=DG?FG=(a﹣b)?b=ab﹣b2<ab,
∵a>b>0,
∴S△ABD>S△DFG.
(2)如图,延长BC,GF交于I,
S阴影=S?ABIG﹣S△ABD﹣S△DFG﹣S△BIF,
∴S阴影=a2﹣ab﹣?b?(a﹣b)﹣?a?(a﹣b)=a2+b2﹣ab;
∴阴影部分的面积用代数式表示为:a2+b2﹣ab;
(3)当a+b=10,ab=20时,a2+b2﹣ab=(a+b)2﹣ab=×102﹣×20=20.
24.解:(1)(ab+3a2)﹣2(a2﹣2ab)
=ab+3a2﹣2a2+4ab
=a2+5ab,
∵|a﹣1|+(b+2)2=0.
∴a=1,b=﹣2,
∴原式=12+5×1×(﹣2)
=1﹣10
=﹣9;
(2)①2A﹣B
=2(x3+2x+3)﹣(2x3﹣xy+2)
=2x3+4x+6﹣2x3+xy﹣2
=xy+4x+4;
②若2A﹣B的值与x无关,则y+4=0,
∴y=﹣4.
25.解:(1)表格每行有10个数字,
2019÷10=201???9,201+1=202,
∴2019在第202行,第9列.
(2)∵被框住的3个数中,最大的一个数为x,
∴另外两个数为x﹣11和x﹣9,
∴x﹣11+x﹣9+x=2020,
解得x=680,680﹣11=669,680﹣9=671,
∵680在第68行第10列,671在67行第1列,
∴被框住的三个数的和不能等于2020.
26.解:(1)A方案购买可列式:50×120+(x﹣50)×20=5000+20x(元);
按B方案购买可列式:(50×120+20x)×0.9=5400+18x(元);
故答案为:(5000+20x),(5400+18x);
(2)当x=100时,
A方案购买需付款:5000+20x=5000+20×100=7000(元);
按B方案购买需付款:5400+18x=5400+18×100=7200(元);
∵7000<7200,
∴当x=100时,应选择A方案购买合算;
(3)由(2)可知,当x=100时,A方案付款7000元,B方案付款7200元,
按A方案购买50个篮球配送50个跳绳,按B方案购买50个跳绳合计需付款:
120×50+20×50×90%=6900,
∵6900<7000<7200,
∴省钱的购买方案是:
按A方案买50个篮球,剩下的50条跳绳按B方案购买,付款6900元.
同课章节目录
