2021-2022学年湘教版数学九年级上册3.4.2相似三角形的性质 同步练习(word解析版)
文档属性
| 名称 | 2021-2022学年湘教版数学九年级上册3.4.2相似三角形的性质 同步练习(word解析版) |  | |
| 格式 | docx | ||
| 文件大小 | 571.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-04 21:41:28 | ||
图片预览



文档简介
相似三角形的性质
一、单选题
1.如图,在中,,,,是上一点,,,垂足为,则(
)
A.2
B.3
C.4
D.5
2.如图,在中,点D,E分别是边和的中点,则与的面积之比为(
)
A.1∶4
B.1∶3
C.1∶2
D.1∶1
3.如图,,若与相似,则等于(
)
A.
B.
C.或
D.或
4.如图,D是的边延长线上一点,且,直线分别交于E,F.若,则(
)
A.
B.
C.
D.
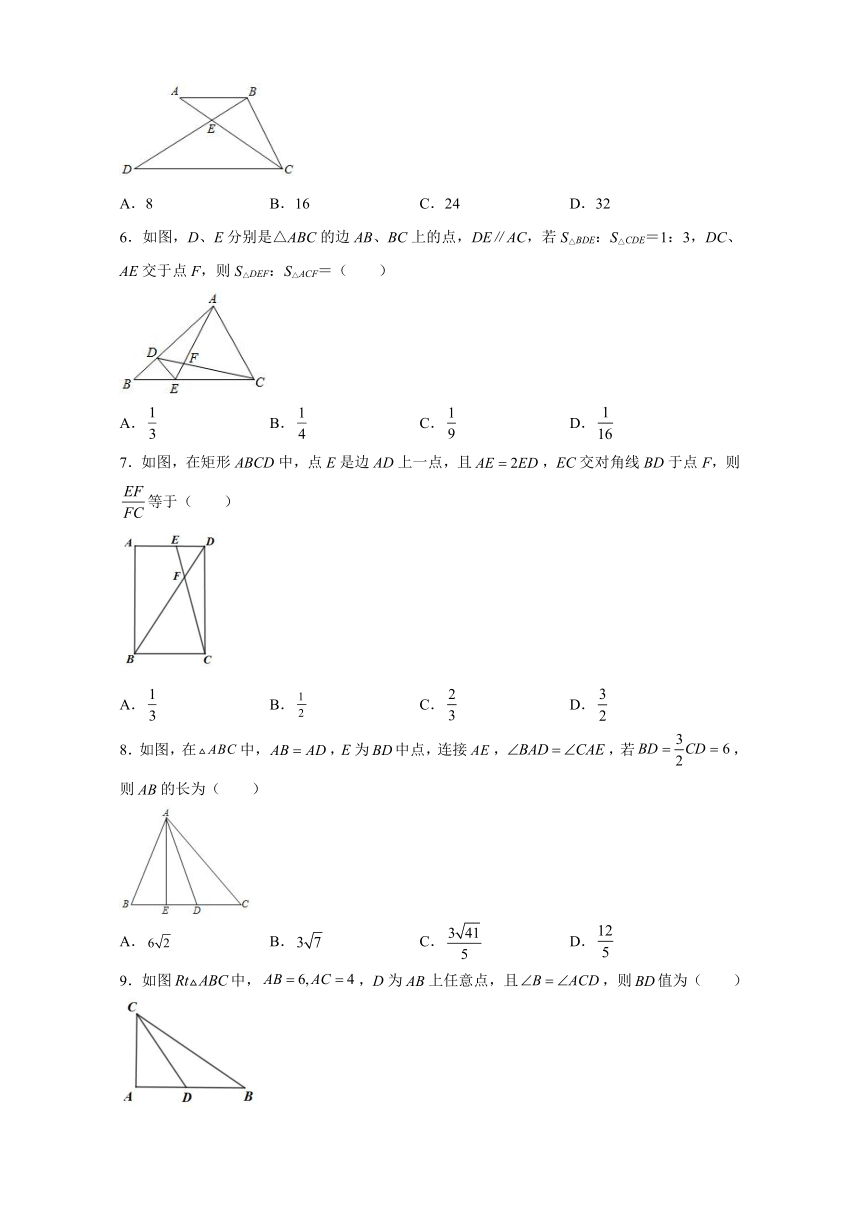
5.如图,在△ABC中,E是线段AC上一点,且AE:CE=1:2,过点C作CD∥AB,交BE的延长线于点D.若△BCE的面积等于4,则△CDE的面积等于( )
A.8
B.16
C.24
D.32
6.如图,D、E分别是△ABC的边AB、BC上的点,DE∥AC,若S△BDE:S△CDE=1:3,DC、AE交于点F,则S△DEF:S△ACF=( )
A.
B.
C.
D.
7.如图,在矩形ABCD中,点E是边AD上一点,且,EC交对角线BD于点F,则等于(
)
A.
B.
C.
D.
8.如图,在中,,E为中点,连接,,若,则的长为(
)
A.
B.
C.
D.
9.如图中,,D为上任意点,且,则值为(
)
A.
B.
C.3
D.
10.如图,在?ABCD中,E为AC的三等分点,AE=AD,连接BE交AC于点F,若△AEF的面积是8,则△BCF的面积为(
)
A.16
B.18
C.24
D.36
11.如图,△ABC∽△DCA,∠B=33°,∠D=117°,则∠BAD的度数是( )
A.150°
B.147°
C.135°
D.120°
12.如图,在平行四边形ABCD中,E是AB的中点,F是AD的中点,FE交AC于O点,交CB的延长线于G点,那么S△AOF:S△COG=( )
A.1:4
B.1:9
C.1:16
D.1:25
13.如图,在正方形ABCD中,点E为AB边的中点,点F在DE上,CF=CD,过点F作FG⊥FC交AD于点G.下列结论:①GF=GD;②AG>AE;③AF⊥DE;④DF=3EF;⑤∠ADF=30°正确的是( )
A.①③
B.①②③
C.①③④
D.①③④⑤
14.两个相似三角形的面积比为1:16,则它们对应边的比是(
)
A.1:16
B.1:8
C.1:4
D.4:1
15.在,且面积比为4:9,则其对应边上的高的比为(
)
A.
B.
C.
D.
二、填空题
16.如图,是的中线,是的中点,连接.若的面积为1,则四边形的面积为_________.
17.如图,在中,CD,BE是的两条中线,则的值为____________.
18.如图,点E是?ABCD边AD的中点,连接AC、BE交于点P,过点P作PQAD交CD于点Q,若AB=3,则DQ=___.
19.如图,在中,,若,,的面积分别为,,,则的面积为________.
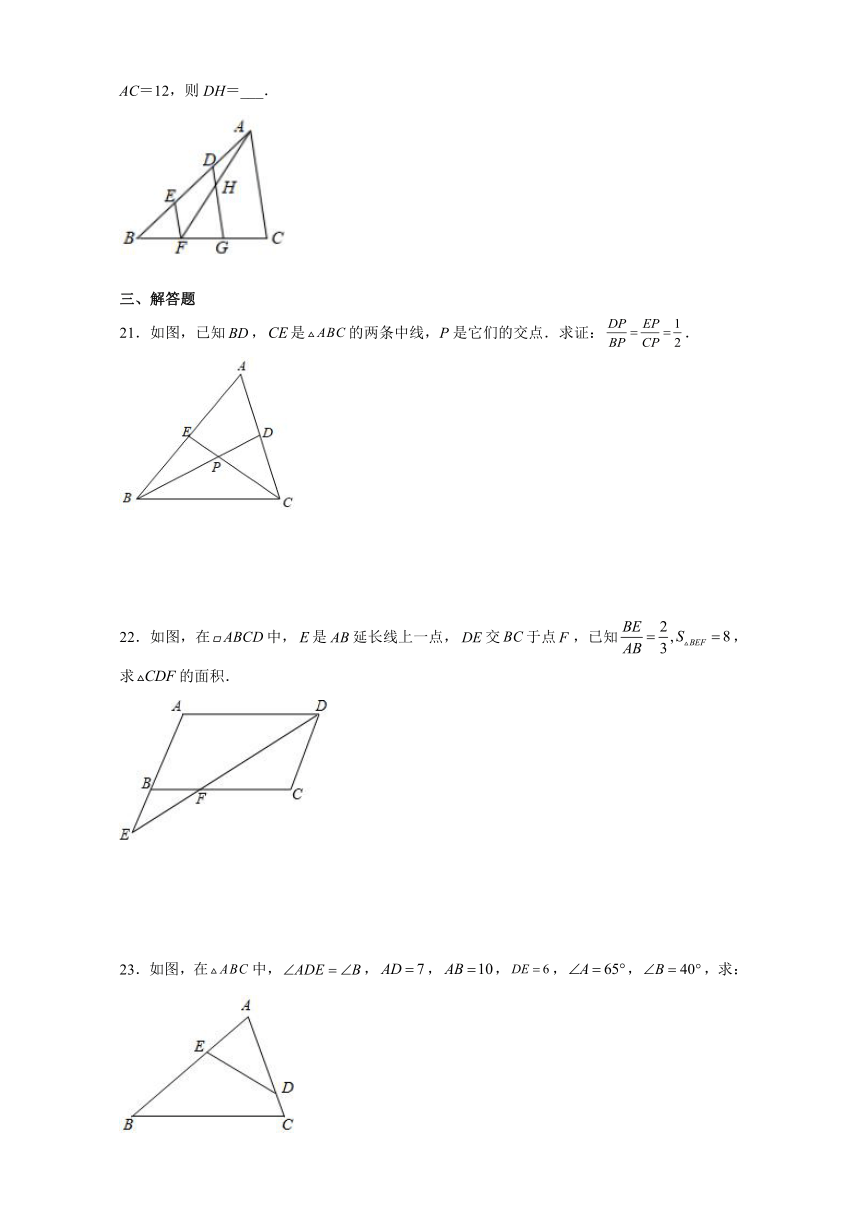
20.如图,在△ABC中,D、E为边AB的三等分点,EF∥DG∥AC,H为AF与DG的交点.若AC=12,则DH=___.
三、解答题
21.如图,已知,是的两条中线,P是它们的交点.求证:.
22.如图,在中,是延长线上一点,交于点,已知,求的面积.
23.如图,在中,,,,,,,求:
(1)与的度数;
(2)的长.
24.如图,在中,点、分别在边,上,,线段分别交线段,于点,,且.
(1)求证:;
(2)若,求的值.
25.如图,CD是直角△ABC斜边AB上的中线,点E位于边AC上,且.
(1)求证:△CDE∽△ACB;
(2)当DA∶EA=时,求△CDE与△ABC的面积比.
26.已知:如图,在?ABCD中,点E、F分别在边BC、边BC的延长线上,四边形AEFD是菱形,菱形的对角线AF分别交DE、DC于点P、Q,.
求证:(1)四边形ABCD为矩形;
(2)BE?DQ=FQ?PE.
参考答案
1.C
解:∵ED⊥AB,
∴∠AED=90°=∠C,
∵∠A=∠A,
∴△ADE∽△ABC,
∴,即,
解得:AE=4.
故选:C.
2.A
解:∵D,E分别是边AB,AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,且DE=BC,
∴△ADE∽△ABC,
∴;
故选:A;
3.D
解:①当时,
则,
即:,
所以要使,只要等于,
当②时,
则,
即:,
解得:,
所以要使,只要等于,
综上可知:或,
故选:D.
4.B
解:如图,作交于.
∴△AEP∽△ABC,△EPF∽△DCF,
,
,
,
,
5.A
解:∵△BCE中CE边上的高和△ABE中AE边上的高相等,且AE:CE=1:2,
∴S△BCE=2S△ABE,
∵S△BCE=4,
∴S△ABE=×4=2,
∵CD∥AB,
∴△ABE∽△CDE,
∴=,
∴==.
∴S△CDE=8,
故答案选:A.
6.D
解:∵,
∴,
∵,
∴,,
∴,
∴,
故选:D.
7.A
解:∵四边形ABCD是矩形,
∴,,
∴,
∵,
∴,
∴;
故选A.
8.A
解:过点D作DFAC于F,如图,
在中,,E为中点,
.
9.D
解:∵,∠CAD=∠BAC=90°,
∴△CAD∽△BAC,
∴,
设,则,解得,
故选:D.
10.B
解:∵四边形ABCD是平行四边形,
,
.
,
,
.
∵△AEF的面积是8,
∴△BCF的面积为,
故选:B.
11.B
解:∵△ABC∽△DCA,
∴∠BAC=∠D=117°,∠DCA=∠B=33°,
∴∠DAC=180°﹣117°﹣33°=30°,
∴∠BAD=∠BAC+∠DAC=147°,
故选:B.
12.B
解:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵E为AB的中点,F为AD的中点,
∴AE=BE,AF=AD=BC,
∵AD∥BC,
∴△AFE∽△BGE,
∴,
∵AE=BE,
∴AF=BG=BC,
∴
∵AD∥BC,
∴△AFO∽△CGO,
∴,
即S△AOF:S△COG=1:9,
故选:B
13.C
解:(1)连接CG,?如图所示:
∵四边形ABCD是正方形,
∴∠ADC=90°,
∵FG⊥FC,
∴∠GFC=90°,
在Rt△CFG与Rt△CDG中,CG=CG,CF=CD
∴RtΔCFG≌RtΔCDG(HL),
∴GF=GD,
故①正确.
(2)由(1),CG垂直平分DF,
∴∠EDC+∠2=90°,
∵∠1+∠EDC=90°,
∴∠1=∠2,
∵四边形ABCD是正方形,
∴AD=DC=AB,∠DAE=∠CDG=90°,
∴ΔADE≌ΔDCG(ASA),
∴AE=DG,
∵E为AB边的中点,
∴G为AD边的中点,
∴AG=AE,
故②错误.
(3)由(2),得GF=GD=GA,
?∴∠AFD=,
故③正确.
(4)由(3),可得ΔAEF∽ΔDAF∽ΔDEA,
?∴,?
∴DF=2AF=4EF,
故④正确.
(5)由(4)知DF=2AF,可得AD=AF,
∴,
故⑤错误.
故选:C.
14.C
解:∵两个相似三角形的面积比为1:16,
∴它们的对应边的比=1:4.
故选:C.
15.C
解:∵,且面积比为4:9,
∴和的相似为2:3,
故对应边上的高的比为2:3,
故选:C.
16.
解:
故答案为:
17.
解:
CD,BE是的两条中线,
是的中位线,
故答案为:
18.1
解:四边形为平行四边形,
,,,
点是的中点,
,
,
,
,
,
,
.
故答案为1.
19.405
解:∵DE∥FG∥BC,GI∥EF∥AB,
∴△ADE∽△EFG∽△GIC,
∴S△ADE:S△EFG=AE2:EG2=20:45,
∴AE:EG=2:3,
∴S△EFG:S△GIC=EG2:GC2=45:80,
∴EG:GC=3:4,
∴AE:AC=2:9,
而△ADE∽△ABC,
∴S△ADE:S△ABC=AE2:AC2=4:81,
∴S△ABC=×20=405cm2.
故答案为:405.
20.2
解:∵D、E为边AB的三等分点,
∴,
∵EF∥DG∥AC,
∴,,
∴,,
∵AC=12,
∴,
∴;
故答案为2.
21.见解析
解:证明:连接,如图:
,是的两条中线.
、是AB、AC的中点.
且.
.
.
.
22.18
解:∵四边形ABCD为平行四边形,
∴CD=AB,且CD∥AB,
∴△CDF∽△BEF,
∵,
∴,
∴,即,
解得S△CDF=18.
23.(1)∠AED=∠C=75°;(2)
解:(1)∵∠A=65°,∠B=40°,
∴∠C=180°-∠A-∠B=75°,
∵∠ADE=∠B,∠A=∠A,
∴△AED∽△ACB,
∴∠AED=∠C=75°,
(2)由(1)知,△AED∽△ACB,
∴,
∴,
∴BC=.
24.(1)见解析;(2)
(1)解:,.
,
,
又,
;
(2)解:,
,
,
,
.
25.(1)见解析;(2)
解:(1)∵CD是直角△ABC斜边上的中线,
∴DC=DA=DB,
∴∠DCA=∠A.
在△ADE中,∠DEC=∠A+∠ADE.
又∠ADE=∠B-∠A,即∠B=∠A+∠ADE,
∴∠DEC=∠B.
∴△CDE∽△ACB.
(2)令EA=k,DA=,CE=x.
由△CDE∽△ACB,
得,即,
解得,(舍).
所以.
26.(1)见解析;(2)见解析
解:(1)∵四边形ADFE是菱形,
∴AF⊥DE,
∴∠EPF=90°,
∵,∠PFE=∠AFB,
∴△ABF∽△EPF,
∴∠ABE=∠EPF=90°,
∴平行四边形ABCD是矩形;
(2)∵四边形ABCD是矩形,
∴AD=BC=EF,
∴EC+CF=BE+CE,
∴BE=CF,
∵∠DPF=∠QCF=90°,∠CQF=∠PQD,
∴△DPQ∽△FCQ,
∴,
∴,
∴BE?DQ=FQ?PE.
一、单选题
1.如图,在中,,,,是上一点,,,垂足为,则(
)
A.2
B.3
C.4
D.5
2.如图,在中,点D,E分别是边和的中点,则与的面积之比为(
)
A.1∶4
B.1∶3
C.1∶2
D.1∶1
3.如图,,若与相似,则等于(
)
A.
B.
C.或
D.或
4.如图,D是的边延长线上一点,且,直线分别交于E,F.若,则(
)
A.
B.
C.
D.
5.如图,在△ABC中,E是线段AC上一点,且AE:CE=1:2,过点C作CD∥AB,交BE的延长线于点D.若△BCE的面积等于4,则△CDE的面积等于( )
A.8
B.16
C.24
D.32
6.如图,D、E分别是△ABC的边AB、BC上的点,DE∥AC,若S△BDE:S△CDE=1:3,DC、AE交于点F,则S△DEF:S△ACF=( )
A.
B.
C.
D.
7.如图,在矩形ABCD中,点E是边AD上一点,且,EC交对角线BD于点F,则等于(
)
A.
B.
C.
D.
8.如图,在中,,E为中点,连接,,若,则的长为(
)
A.
B.
C.
D.
9.如图中,,D为上任意点,且,则值为(
)
A.
B.
C.3
D.
10.如图,在?ABCD中,E为AC的三等分点,AE=AD,连接BE交AC于点F,若△AEF的面积是8,则△BCF的面积为(
)
A.16
B.18
C.24
D.36
11.如图,△ABC∽△DCA,∠B=33°,∠D=117°,则∠BAD的度数是( )
A.150°
B.147°
C.135°
D.120°
12.如图,在平行四边形ABCD中,E是AB的中点,F是AD的中点,FE交AC于O点,交CB的延长线于G点,那么S△AOF:S△COG=( )
A.1:4
B.1:9
C.1:16
D.1:25
13.如图,在正方形ABCD中,点E为AB边的中点,点F在DE上,CF=CD,过点F作FG⊥FC交AD于点G.下列结论:①GF=GD;②AG>AE;③AF⊥DE;④DF=3EF;⑤∠ADF=30°正确的是( )
A.①③
B.①②③
C.①③④
D.①③④⑤
14.两个相似三角形的面积比为1:16,则它们对应边的比是(
)
A.1:16
B.1:8
C.1:4
D.4:1
15.在,且面积比为4:9,则其对应边上的高的比为(
)
A.
B.
C.
D.
二、填空题
16.如图,是的中线,是的中点,连接.若的面积为1,则四边形的面积为_________.
17.如图,在中,CD,BE是的两条中线,则的值为____________.
18.如图,点E是?ABCD边AD的中点,连接AC、BE交于点P,过点P作PQAD交CD于点Q,若AB=3,则DQ=___.
19.如图,在中,,若,,的面积分别为,,,则的面积为________.
20.如图,在△ABC中,D、E为边AB的三等分点,EF∥DG∥AC,H为AF与DG的交点.若AC=12,则DH=___.
三、解答题
21.如图,已知,是的两条中线,P是它们的交点.求证:.
22.如图,在中,是延长线上一点,交于点,已知,求的面积.
23.如图,在中,,,,,,,求:
(1)与的度数;
(2)的长.
24.如图,在中,点、分别在边,上,,线段分别交线段,于点,,且.
(1)求证:;
(2)若,求的值.
25.如图,CD是直角△ABC斜边AB上的中线,点E位于边AC上,且.
(1)求证:△CDE∽△ACB;
(2)当DA∶EA=时,求△CDE与△ABC的面积比.
26.已知:如图,在?ABCD中,点E、F分别在边BC、边BC的延长线上,四边形AEFD是菱形,菱形的对角线AF分别交DE、DC于点P、Q,.
求证:(1)四边形ABCD为矩形;
(2)BE?DQ=FQ?PE.
参考答案
1.C
解:∵ED⊥AB,
∴∠AED=90°=∠C,
∵∠A=∠A,
∴△ADE∽△ABC,
∴,即,
解得:AE=4.
故选:C.
2.A
解:∵D,E分别是边AB,AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,且DE=BC,
∴△ADE∽△ABC,
∴;
故选:A;
3.D
解:①当时,
则,
即:,
所以要使,只要等于,
当②时,
则,
即:,
解得:,
所以要使,只要等于,
综上可知:或,
故选:D.
4.B
解:如图,作交于.
∴△AEP∽△ABC,△EPF∽△DCF,
,
,
,
,
5.A
解:∵△BCE中CE边上的高和△ABE中AE边上的高相等,且AE:CE=1:2,
∴S△BCE=2S△ABE,
∵S△BCE=4,
∴S△ABE=×4=2,
∵CD∥AB,
∴△ABE∽△CDE,
∴=,
∴==.
∴S△CDE=8,
故答案选:A.
6.D
解:∵,
∴,
∵,
∴,,
∴,
∴,
故选:D.
7.A
解:∵四边形ABCD是矩形,
∴,,
∴,
∵,
∴,
∴;
故选A.
8.A
解:过点D作DFAC于F,如图,
在中,,E为中点,
.
9.D
解:∵,∠CAD=∠BAC=90°,
∴△CAD∽△BAC,
∴,
设,则,解得,
故选:D.
10.B
解:∵四边形ABCD是平行四边形,
,
.
,
,
.
∵△AEF的面积是8,
∴△BCF的面积为,
故选:B.
11.B
解:∵△ABC∽△DCA,
∴∠BAC=∠D=117°,∠DCA=∠B=33°,
∴∠DAC=180°﹣117°﹣33°=30°,
∴∠BAD=∠BAC+∠DAC=147°,
故选:B.
12.B
解:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵E为AB的中点,F为AD的中点,
∴AE=BE,AF=AD=BC,
∵AD∥BC,
∴△AFE∽△BGE,
∴,
∵AE=BE,
∴AF=BG=BC,
∴
∵AD∥BC,
∴△AFO∽△CGO,
∴,
即S△AOF:S△COG=1:9,
故选:B
13.C
解:(1)连接CG,?如图所示:
∵四边形ABCD是正方形,
∴∠ADC=90°,
∵FG⊥FC,
∴∠GFC=90°,
在Rt△CFG与Rt△CDG中,CG=CG,CF=CD
∴RtΔCFG≌RtΔCDG(HL),
∴GF=GD,
故①正确.
(2)由(1),CG垂直平分DF,
∴∠EDC+∠2=90°,
∵∠1+∠EDC=90°,
∴∠1=∠2,
∵四边形ABCD是正方形,
∴AD=DC=AB,∠DAE=∠CDG=90°,
∴ΔADE≌ΔDCG(ASA),
∴AE=DG,
∵E为AB边的中点,
∴G为AD边的中点,
∴AG=AE,
故②错误.
(3)由(2),得GF=GD=GA,
?∴∠AFD=,
故③正确.
(4)由(3),可得ΔAEF∽ΔDAF∽ΔDEA,
?∴,?
∴DF=2AF=4EF,
故④正确.
(5)由(4)知DF=2AF,可得AD=AF,
∴,
故⑤错误.
故选:C.
14.C
解:∵两个相似三角形的面积比为1:16,
∴它们的对应边的比=1:4.
故选:C.
15.C
解:∵,且面积比为4:9,
∴和的相似为2:3,
故对应边上的高的比为2:3,
故选:C.
16.
解:
故答案为:
17.
解:
CD,BE是的两条中线,
是的中位线,
故答案为:
18.1
解:四边形为平行四边形,
,,,
点是的中点,
,
,
,
,
,
,
.
故答案为1.
19.405
解:∵DE∥FG∥BC,GI∥EF∥AB,
∴△ADE∽△EFG∽△GIC,
∴S△ADE:S△EFG=AE2:EG2=20:45,
∴AE:EG=2:3,
∴S△EFG:S△GIC=EG2:GC2=45:80,
∴EG:GC=3:4,
∴AE:AC=2:9,
而△ADE∽△ABC,
∴S△ADE:S△ABC=AE2:AC2=4:81,
∴S△ABC=×20=405cm2.
故答案为:405.
20.2
解:∵D、E为边AB的三等分点,
∴,
∵EF∥DG∥AC,
∴,,
∴,,
∵AC=12,
∴,
∴;
故答案为2.
21.见解析
解:证明:连接,如图:
,是的两条中线.
、是AB、AC的中点.
且.
.
.
.
22.18
解:∵四边形ABCD为平行四边形,
∴CD=AB,且CD∥AB,
∴△CDF∽△BEF,
∵,
∴,
∴,即,
解得S△CDF=18.
23.(1)∠AED=∠C=75°;(2)
解:(1)∵∠A=65°,∠B=40°,
∴∠C=180°-∠A-∠B=75°,
∵∠ADE=∠B,∠A=∠A,
∴△AED∽△ACB,
∴∠AED=∠C=75°,
(2)由(1)知,△AED∽△ACB,
∴,
∴,
∴BC=.
24.(1)见解析;(2)
(1)解:,.
,
,
又,
;
(2)解:,
,
,
,
.
25.(1)见解析;(2)
解:(1)∵CD是直角△ABC斜边上的中线,
∴DC=DA=DB,
∴∠DCA=∠A.
在△ADE中,∠DEC=∠A+∠ADE.
又∠ADE=∠B-∠A,即∠B=∠A+∠ADE,
∴∠DEC=∠B.
∴△CDE∽△ACB.
(2)令EA=k,DA=,CE=x.
由△CDE∽△ACB,
得,即,
解得,(舍).
所以.
26.(1)见解析;(2)见解析
解:(1)∵四边形ADFE是菱形,
∴AF⊥DE,
∴∠EPF=90°,
∵,∠PFE=∠AFB,
∴△ABF∽△EPF,
∴∠ABE=∠EPF=90°,
∴平行四边形ABCD是矩形;
(2)∵四边形ABCD是矩形,
∴AD=BC=EF,
∴EC+CF=BE+CE,
∴BE=CF,
∵∠DPF=∠QCF=90°,∠CQF=∠PQD,
∴△DPQ∽△FCQ,
∴,
∴,
∴BE?DQ=FQ?PE.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
