2021-2022学年湘教版数学九年级上册3.4.1相似三角形的判定 同步练习(word版含答案)
文档属性
| 名称 | 2021-2022学年湘教版数学九年级上册3.4.1相似三角形的判定 同步练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 480.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-05 08:04:45 | ||
图片预览



文档简介
相似三角形的判定
一、单选题
1.下列命题中,假命题为(
)
A.锐角三角形和钝角三角形一定不相似
B.直角三角形都相似
C.两条直角边成比例的两个直角三角形相似
D.如果一个三角形的3条高与另一个三角形的3条高对应成比例,那么这两个三角形相似
2.如图,四个三角形的顶点都在方格子的格点上,下列两个三角形中相似的是(
)
A.①④
B.①③
C.②③
D.②④
3.如图,已知,那么添加一个条件后,依然无法判定∽(
)
A.
B.
C.
D.
4.如图,要使∽,需补充的条件不能是(
)
A.
B.
C.
D.
5.平面直角坐标系中,直线和x、y轴交于A、B两点,在第二象限内找一点P,使△PAO和△AOB相似的三角形个数为(
)
A.2
B.3
C.4
D.5
6.如图所示,给出下列哪个条件单独能够判定的是(
)
A.
B.
C.
D.
7.若是斜边上异于,的一点,过点作直线截,截得的三角形与原相似,满足这样条件的直线有(
)条.
A.1
B.2
C.3
D.4
8.已知在△ABC中,AB=6,AC=4,点P
是AC的中点,过P的直线交AB于Q,若想得到以A、P、Q为顶点的三角形与△ABC相似,则AQ的长为(
)
A.3
B.或
C.3或
D.10
9.下列说法中,错误的是(
)
A.所有的等边三角形都相似
B.所有的矩形都相似
C.所有的等腰直角三角形都相似
D.所有的正方形都相似
10.如图,四边形,四边形,四边形都是正方形,图中与相似的三角形为(
)
A.
B.
C.
D.
11.如图,在中,点D、E分别在边、上,则在下列五个条件中:①;②;③;④,能满足的条件有( )
A.1个
B.2个
C.3个
D.4个
12.如图,、是锐角两边、上的高,它们交于点,图中共有几对相似三角形(
)
A.3对
B.4对
C.5对
D.6对
13.如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的( )
A.
B.
C.
D.
14.如图所示,是上的点,,则下列结论正确的是(
)
A.
B.
C.
D.以上都不对
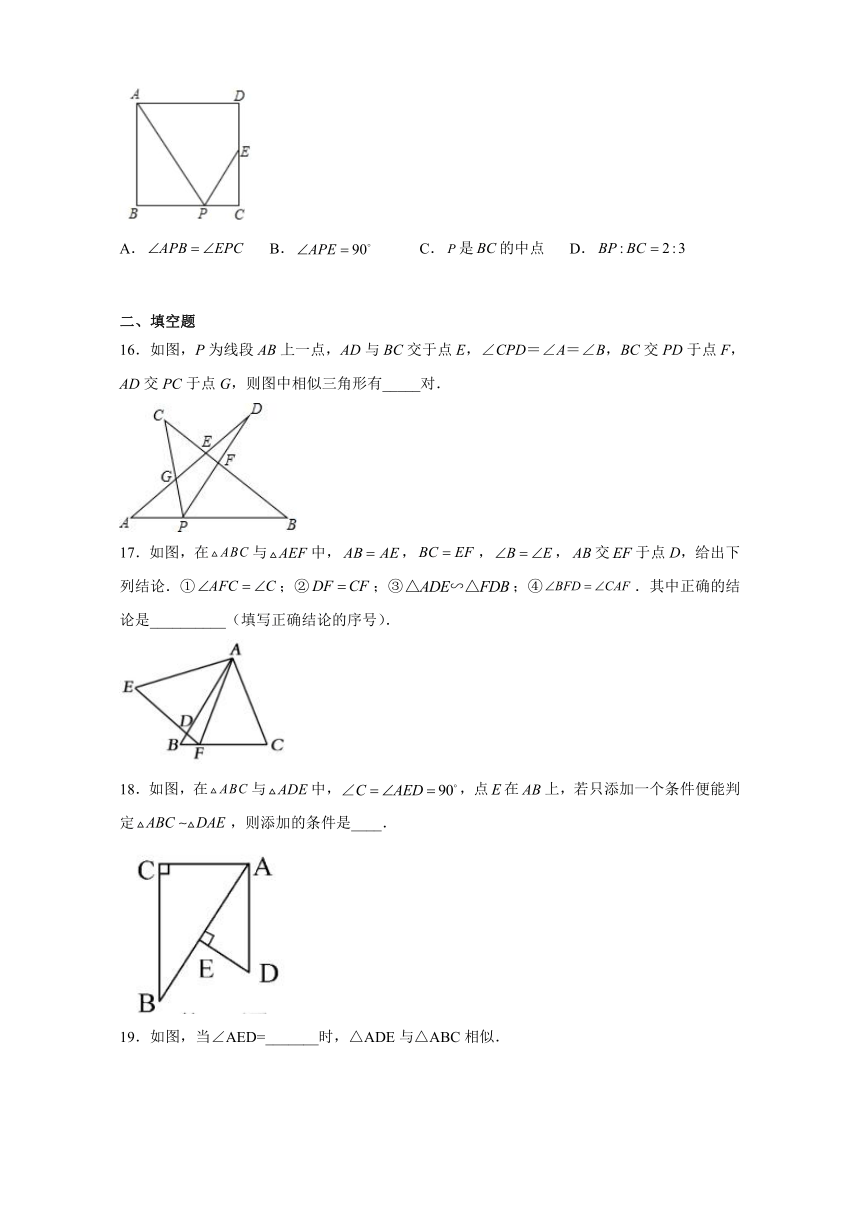
15.如图,正方形中,是的中点,是边上的一点,下列条件中,不能推出与相似的是(
)
A.
B.
C.是的中点
D.
二、填空题
16.如图,P为线段AB上一点,AD与BC交于点E,∠CPD=∠A=∠B,BC交PD于点F,AD交PC于点G,则图中相似三角形有_____对.
17.如图,在与中,,,,交于点D,给出下列结论.①;②;③;④.其中正确的结论是__________(填写正确结论的序号).
18.如图,在与中,,点在上,若只添加一个条件便能判定,则添加的条件是____.
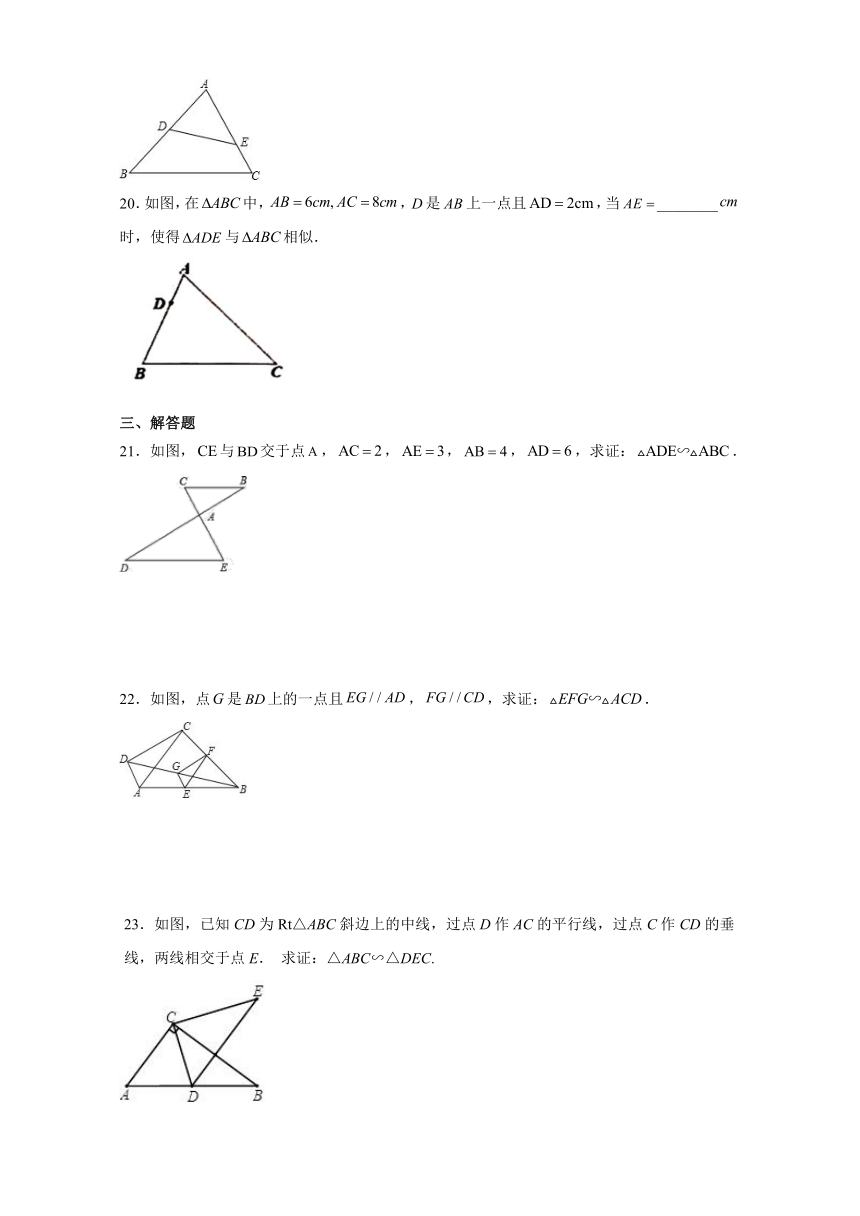
19.如图,当∠AED=_______时,△ADE与△ABC相似.
20.如图,在中,,是上一点且,当________时,使得与相似.
三、解答题
21.如图,与交于点,,,,,求证:.
22.如图,点是上的一点且,,求证:.
23.如图,已知CD为Rt△ABC斜边上的中线,过点D作AC的平行线,过点C作CD的垂线,两线相交于点E.
求证:△ABC∽△DEC.
24.如图,点E是四边形ABCD的对角线BD上一点,且∠BAC=∠BDC=∠DAE.求证:△ABE∽△ACD.
25.如图,点D、E分别在AB、AC边上,且AD=5,BD=3,AE=4,CE=6.
试说明:(1)△ADE∽△ACB;(2)若BC=9,求DE的长.
26.已知:如图,在△ABC中,点D、E分别在边AB、AC上,且∠ABE
=∠ACD,BE、CD交于点G.
(1)求证:△AED∽△ABC;
(2)如果BE平分∠ABC,求证:DE=CE.
参考答案
1.B
解:A、锐角三角形和钝角三角形一定不相似,是真命题,不符合题意;
B、直角三角形不一定相似,故原命题是假命题,符合题意;
C、两条直角边成比例的两个直角三角形相似,是真命题,不符合题意;
D、如果一个三角形的3条高与另一个三角形的3条高对应成比例,那么这两个三角形相似,是真命题,不符合题意,
故选:B.
2.B
解:三角形①的三边分别为;三角形②的三边分别为:;三角形③的三边分别为;三角形④的三边分别为:.显然三角形①③的三边成比例,即,即三角形①③相似.
故选:B.
3.D
解:,
,
、若,且,可判定,故选项不符合题意;
、若,且,可判定,故选项不符合题意;
、若,且,可判定,故选项不符合题意;
、若,且,无法判定,故选项符合题意;
故选:.
4.D
解:∵
∴当或或时,∽,
故选:D.
5.C
解:如图,
①分别过点O、点A作AB、OB的平行线交于点P1,则△OAP1与△AOB相似(全等),
②作AP2⊥OP1,垂足为P2则△AOP2与△AOB相似.
③作∠AOP3=∠ABO交AP1于P3,则△AOP3与△AOB相似.
④作AP4⊥OP3垂足为P4,则△AOP4与△AOB相似.
故选C.
6.C
解:A.,不能判定的两个三角形相似,不符合题意;
B.竖向确定三角形△ACD与△ABC,夹角与∠B不一定相等,横向确定三角形△ABC与△CBD,夹角∠A与∠DCB不一定相等,不能判定的两个三角形相似,不符合题意,
C.由变形得,,由∠BAC=∠CAD,则,
可以根据两组对应边成比例且夹角相等的两个三角形相似来判定,符合题意;
D.竖向确定三角形△ADC与△BCD,夹角与∠DCB不一定相等,横向确定三角形△ADC与△ACB,夹角∠ADC与∠ACB不一定相等,不能判定的两个三角形相似,不符合题意;
故选择:.
7.C
解:由于是直角三角形,
过点作直线截,则截得的三角形与有一公共角,
所以只要再作一个直角即可使截得的三角形与相似,
过点可作的垂线、的垂线、的垂线,共3条直线.
故选:.
8.B
解:分两种情况讨论
第一种情况,如下图
当,即,得AQ=3时,得△APQ∽△ACB;
第二种情况,如下图
当,即,得AQ=时,得△APQ∽△ABC;
∴AQ的长为或.
故选:B.
9.B
解:A.所有的等边三角形都相似,故本选项选项为真命题;
B.所有的矩形不一定相似,如一个矩形的长宽之比为,另一个矩形的长宽之比为,故本选项选项为假命题;
C.所有的等腰直角三角形都相似,故本选项选项为真命题;
D.所有的正方形都相似,故本选项选项为真命题.
故选:B
10.A
解:设正方形ABGH的边长为1,
∴DF=,DG=,
∴GF:DF:DG=1::,
A、DF=,DH=,HF=2,DF:HF:DH=GF:DF:DG,
则△DFG∽△HFD,符合题意;
B、HG=1,DG=,DH=,HG:DG:DH≠GF:DF:DG,
则△DFG和△DGH不相似,不符合题意;
C、△DEG是直角三角形,△DFG是钝角三角形,故不相似,不符合题意;
D、△DEH是直角三角形,△DFG是钝角三角形,故不相似,不符合题意;
故选A.
11.B
解:①在和中,,
,则条件①能满足;
②,
,则条件②不能满足;
③在和中,,
,则条件③能满足;
④由得:,
对应的夹角与不一定相等,
此时和不一定相似,则条件④不能满足;
综上,能满足的条件有2个,
故选:B.
12.D
解:先找出相似的三角形由△ABF,△ACE,△DBE,△DCF,
△ABF与△ACE,△DBE,△DCF都相似,有3对,
△ACE与△DBE,△DCF都相似,有2对,
△DBE与△DCF都相似,有1对,
相似的三角形共有3+2+1=6对.
故选择:D.
13.C
解:∵∠BAC=∠D,
∴△ABC∽△ADE.
故选C.
14.B
解:∵∠ADC=∠BAC,∠ABC=∠DAC,
∴△ABC∽△DAC.
故选:B.
15.C
解:A.
,根据正方形性质得到∠B=∠C,可以得到∽,不合题意;
B.
,根据正方形性质得到∠B=∠C,根据同角的余角相等,得到,可以得到∽,不合题意;
C.
是的中点,无法判断与相似,符合题意;
D.
,根据正方形性质得到,又∵∠B=∠C,可以得到∽,不合题意.
故选:C
16.3
解:∵∠CPD=∠B,∠C=∠C,
∴△PCF∽△BCP.
∵∠CPD=∠A,∠D=∠D,
∴△APD∽△PGD.
∵∠CPD=∠A=∠B,∠APG=∠B+∠C,∠BFP=∠CPD+∠C
∴∠APG=∠BFP,
∴△APG∽△BFP.
则图中相似三角形有3对,
故答案为:3.
17.①③④
解:在△AEF和△ABC中
∵,
∴△AEF≌△ABC(SAS),
∴AF=AC,
∴∠AFC=∠C,
∴①正确;
不正确,理由是:假设,
∵△AEF≌△ABC
∴∠AFD=∠C,AF=AC,
∴△ACF≌△AFD,
∴∠DAF=∠FAC,
原题中无AF为∠BAC平分线这一条件,
∴②错误;
∵∠E=∠B,∠EDA=∠BDF,
∴△ADE∽△FDB,
∴③正确;
∵△AEF≌△ABC,
∴∠EAF=∠BAC,
∴∠EAF﹣∠DAF=∠BAC﹣∠DAF,
∴∠EAD=∠CAF,
∵△ADE∽△FBD,
∴∠BFD=∠EAD=∠CAF,
∴④正确;
故答案为:①③④
18.(答案不唯一).
解:依据两角相等,两三角形相似,可添加条件
故答案为:(答案不唯一).
19.∠ACB或∠ABC
解:∵∠BAC=∠EAD(公共角),
再由∠AED=∠ACB或∠AED=∠ABC,
即可证明,△ADE与△ABC相似,
故答案为:∠ACB或∠ABC.
20.或1.5
解:分两种情况:
第一种情况:如图,过D作DE||AC于点E,
则;
第二种情况:如图,ΔADEΔACB
则
故答案为.
21.见解析.
解:∵,,
∴,
∵∠DAE=∠BAC,
∴△ADE∽△ABC.
22.见解析.
解::∵,
∴,,
∴,
∵,
∴,,
∴,
∵,,
∴.
23.见解析
解:∵CD为Rt△ABC斜边上的中线,
∴.
∴.
∵DE∥AC.
∴.
∴.
∵,CE⊥CD,
∴
.
∴△ABC∽△DEC.
24.见解析.
解:∵∠BAC=∠BDC,∠AOB=∠DOC,
∴∠ABE=∠ACD
又∵∠BAC=∠DAE
∴∠BAC+∠EAC=∠DAE+∠EAC
∴∠DAC=∠EAB
∴△ABE∽△ACD.
25.(1)证明见解析;(2)DE=4.5
解:⑴
∵AD=5,BD=3,AE=4,CE=6,
∴AB=8,AC=10,
∴,
∵∠A=∠A,
∴△ADE∽△ACB;
⑵
∵△ADE∽△ACB,
∴,
∵BC=9,
∴DE=4.5.
26.(1)证明见解析;(2)证明见解析.
解:(1)∵∠ABE
=∠ACD,且∠A是公共角,
∴△ABE∽△ACD.
∴,即,
又∵∠A是公共角,
∴△AED∽△ABC.
(2)在BC上截取BF=BD,连接EF,
在△BDE与△BFE中,BD=BF,∠DBE=∠FBE,BE=BE,
∴△BDE≌△BFE,
∴DE=FE,∠BDE=∠BFE,∴∠ADE=∠EFC,
∵△AED∽△ABC,∴∠ADE=∠ACB,
∴∠EFC=∠ACB,
∴EF=EC,
∴DE=CE.
一、单选题
1.下列命题中,假命题为(
)
A.锐角三角形和钝角三角形一定不相似
B.直角三角形都相似
C.两条直角边成比例的两个直角三角形相似
D.如果一个三角形的3条高与另一个三角形的3条高对应成比例,那么这两个三角形相似
2.如图,四个三角形的顶点都在方格子的格点上,下列两个三角形中相似的是(
)
A.①④
B.①③
C.②③
D.②④
3.如图,已知,那么添加一个条件后,依然无法判定∽(
)
A.
B.
C.
D.
4.如图,要使∽,需补充的条件不能是(
)
A.
B.
C.
D.
5.平面直角坐标系中,直线和x、y轴交于A、B两点,在第二象限内找一点P,使△PAO和△AOB相似的三角形个数为(
)
A.2
B.3
C.4
D.5
6.如图所示,给出下列哪个条件单独能够判定的是(
)
A.
B.
C.
D.
7.若是斜边上异于,的一点,过点作直线截,截得的三角形与原相似,满足这样条件的直线有(
)条.
A.1
B.2
C.3
D.4
8.已知在△ABC中,AB=6,AC=4,点P
是AC的中点,过P的直线交AB于Q,若想得到以A、P、Q为顶点的三角形与△ABC相似,则AQ的长为(
)
A.3
B.或
C.3或
D.10
9.下列说法中,错误的是(
)
A.所有的等边三角形都相似
B.所有的矩形都相似
C.所有的等腰直角三角形都相似
D.所有的正方形都相似
10.如图,四边形,四边形,四边形都是正方形,图中与相似的三角形为(
)
A.
B.
C.
D.
11.如图,在中,点D、E分别在边、上,则在下列五个条件中:①;②;③;④,能满足的条件有( )
A.1个
B.2个
C.3个
D.4个
12.如图,、是锐角两边、上的高,它们交于点,图中共有几对相似三角形(
)
A.3对
B.4对
C.5对
D.6对
13.如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的( )
A.
B.
C.
D.
14.如图所示,是上的点,,则下列结论正确的是(
)
A.
B.
C.
D.以上都不对
15.如图,正方形中,是的中点,是边上的一点,下列条件中,不能推出与相似的是(
)
A.
B.
C.是的中点
D.
二、填空题
16.如图,P为线段AB上一点,AD与BC交于点E,∠CPD=∠A=∠B,BC交PD于点F,AD交PC于点G,则图中相似三角形有_____对.
17.如图,在与中,,,,交于点D,给出下列结论.①;②;③;④.其中正确的结论是__________(填写正确结论的序号).
18.如图,在与中,,点在上,若只添加一个条件便能判定,则添加的条件是____.
19.如图,当∠AED=_______时,△ADE与△ABC相似.
20.如图,在中,,是上一点且,当________时,使得与相似.
三、解答题
21.如图,与交于点,,,,,求证:.
22.如图,点是上的一点且,,求证:.
23.如图,已知CD为Rt△ABC斜边上的中线,过点D作AC的平行线,过点C作CD的垂线,两线相交于点E.
求证:△ABC∽△DEC.
24.如图,点E是四边形ABCD的对角线BD上一点,且∠BAC=∠BDC=∠DAE.求证:△ABE∽△ACD.
25.如图,点D、E分别在AB、AC边上,且AD=5,BD=3,AE=4,CE=6.
试说明:(1)△ADE∽△ACB;(2)若BC=9,求DE的长.
26.已知:如图,在△ABC中,点D、E分别在边AB、AC上,且∠ABE
=∠ACD,BE、CD交于点G.
(1)求证:△AED∽△ABC;
(2)如果BE平分∠ABC,求证:DE=CE.
参考答案
1.B
解:A、锐角三角形和钝角三角形一定不相似,是真命题,不符合题意;
B、直角三角形不一定相似,故原命题是假命题,符合题意;
C、两条直角边成比例的两个直角三角形相似,是真命题,不符合题意;
D、如果一个三角形的3条高与另一个三角形的3条高对应成比例,那么这两个三角形相似,是真命题,不符合题意,
故选:B.
2.B
解:三角形①的三边分别为;三角形②的三边分别为:;三角形③的三边分别为;三角形④的三边分别为:.显然三角形①③的三边成比例,即,即三角形①③相似.
故选:B.
3.D
解:,
,
、若,且,可判定,故选项不符合题意;
、若,且,可判定,故选项不符合题意;
、若,且,可判定,故选项不符合题意;
、若,且,无法判定,故选项符合题意;
故选:.
4.D
解:∵
∴当或或时,∽,
故选:D.
5.C
解:如图,
①分别过点O、点A作AB、OB的平行线交于点P1,则△OAP1与△AOB相似(全等),
②作AP2⊥OP1,垂足为P2则△AOP2与△AOB相似.
③作∠AOP3=∠ABO交AP1于P3,则△AOP3与△AOB相似.
④作AP4⊥OP3垂足为P4,则△AOP4与△AOB相似.
故选C.
6.C
解:A.,不能判定的两个三角形相似,不符合题意;
B.竖向确定三角形△ACD与△ABC,夹角与∠B不一定相等,横向确定三角形△ABC与△CBD,夹角∠A与∠DCB不一定相等,不能判定的两个三角形相似,不符合题意,
C.由变形得,,由∠BAC=∠CAD,则,
可以根据两组对应边成比例且夹角相等的两个三角形相似来判定,符合题意;
D.竖向确定三角形△ADC与△BCD,夹角与∠DCB不一定相等,横向确定三角形△ADC与△ACB,夹角∠ADC与∠ACB不一定相等,不能判定的两个三角形相似,不符合题意;
故选择:.
7.C
解:由于是直角三角形,
过点作直线截,则截得的三角形与有一公共角,
所以只要再作一个直角即可使截得的三角形与相似,
过点可作的垂线、的垂线、的垂线,共3条直线.
故选:.
8.B
解:分两种情况讨论
第一种情况,如下图
当,即,得AQ=3时,得△APQ∽△ACB;
第二种情况,如下图
当,即,得AQ=时,得△APQ∽△ABC;
∴AQ的长为或.
故选:B.
9.B
解:A.所有的等边三角形都相似,故本选项选项为真命题;
B.所有的矩形不一定相似,如一个矩形的长宽之比为,另一个矩形的长宽之比为,故本选项选项为假命题;
C.所有的等腰直角三角形都相似,故本选项选项为真命题;
D.所有的正方形都相似,故本选项选项为真命题.
故选:B
10.A
解:设正方形ABGH的边长为1,
∴DF=,DG=,
∴GF:DF:DG=1::,
A、DF=,DH=,HF=2,DF:HF:DH=GF:DF:DG,
则△DFG∽△HFD,符合题意;
B、HG=1,DG=,DH=,HG:DG:DH≠GF:DF:DG,
则△DFG和△DGH不相似,不符合题意;
C、△DEG是直角三角形,△DFG是钝角三角形,故不相似,不符合题意;
D、△DEH是直角三角形,△DFG是钝角三角形,故不相似,不符合题意;
故选A.
11.B
解:①在和中,,
,则条件①能满足;
②,
,则条件②不能满足;
③在和中,,
,则条件③能满足;
④由得:,
对应的夹角与不一定相等,
此时和不一定相似,则条件④不能满足;
综上,能满足的条件有2个,
故选:B.
12.D
解:先找出相似的三角形由△ABF,△ACE,△DBE,△DCF,
△ABF与△ACE,△DBE,△DCF都相似,有3对,
△ACE与△DBE,△DCF都相似,有2对,
△DBE与△DCF都相似,有1对,
相似的三角形共有3+2+1=6对.
故选择:D.
13.C
解:∵∠BAC=∠D,
∴△ABC∽△ADE.
故选C.
14.B
解:∵∠ADC=∠BAC,∠ABC=∠DAC,
∴△ABC∽△DAC.
故选:B.
15.C
解:A.
,根据正方形性质得到∠B=∠C,可以得到∽,不合题意;
B.
,根据正方形性质得到∠B=∠C,根据同角的余角相等,得到,可以得到∽,不合题意;
C.
是的中点,无法判断与相似,符合题意;
D.
,根据正方形性质得到,又∵∠B=∠C,可以得到∽,不合题意.
故选:C
16.3
解:∵∠CPD=∠B,∠C=∠C,
∴△PCF∽△BCP.
∵∠CPD=∠A,∠D=∠D,
∴△APD∽△PGD.
∵∠CPD=∠A=∠B,∠APG=∠B+∠C,∠BFP=∠CPD+∠C
∴∠APG=∠BFP,
∴△APG∽△BFP.
则图中相似三角形有3对,
故答案为:3.
17.①③④
解:在△AEF和△ABC中
∵,
∴△AEF≌△ABC(SAS),
∴AF=AC,
∴∠AFC=∠C,
∴①正确;
不正确,理由是:假设,
∵△AEF≌△ABC
∴∠AFD=∠C,AF=AC,
∴△ACF≌△AFD,
∴∠DAF=∠FAC,
原题中无AF为∠BAC平分线这一条件,
∴②错误;
∵∠E=∠B,∠EDA=∠BDF,
∴△ADE∽△FDB,
∴③正确;
∵△AEF≌△ABC,
∴∠EAF=∠BAC,
∴∠EAF﹣∠DAF=∠BAC﹣∠DAF,
∴∠EAD=∠CAF,
∵△ADE∽△FBD,
∴∠BFD=∠EAD=∠CAF,
∴④正确;
故答案为:①③④
18.(答案不唯一).
解:依据两角相等,两三角形相似,可添加条件
故答案为:(答案不唯一).
19.∠ACB或∠ABC
解:∵∠BAC=∠EAD(公共角),
再由∠AED=∠ACB或∠AED=∠ABC,
即可证明,△ADE与△ABC相似,
故答案为:∠ACB或∠ABC.
20.或1.5
解:分两种情况:
第一种情况:如图,过D作DE||AC于点E,
则;
第二种情况:如图,ΔADEΔACB
则
故答案为.
21.见解析.
解:∵,,
∴,
∵∠DAE=∠BAC,
∴△ADE∽△ABC.
22.见解析.
解::∵,
∴,,
∴,
∵,
∴,,
∴,
∵,,
∴.
23.见解析
解:∵CD为Rt△ABC斜边上的中线,
∴.
∴.
∵DE∥AC.
∴.
∴.
∵,CE⊥CD,
∴
.
∴△ABC∽△DEC.
24.见解析.
解:∵∠BAC=∠BDC,∠AOB=∠DOC,
∴∠ABE=∠ACD
又∵∠BAC=∠DAE
∴∠BAC+∠EAC=∠DAE+∠EAC
∴∠DAC=∠EAB
∴△ABE∽△ACD.
25.(1)证明见解析;(2)DE=4.5
解:⑴
∵AD=5,BD=3,AE=4,CE=6,
∴AB=8,AC=10,
∴,
∵∠A=∠A,
∴△ADE∽△ACB;
⑵
∵△ADE∽△ACB,
∴,
∵BC=9,
∴DE=4.5.
26.(1)证明见解析;(2)证明见解析.
解:(1)∵∠ABE
=∠ACD,且∠A是公共角,
∴△ABE∽△ACD.
∴,即,
又∵∠A是公共角,
∴△AED∽△ABC.
(2)在BC上截取BF=BD,连接EF,
在△BDE与△BFE中,BD=BF,∠DBE=∠FBE,BE=BE,
∴△BDE≌△BFE,
∴DE=FE,∠BDE=∠BFE,∴∠ADE=∠EFC,
∵△AED∽△ABC,∴∠ADE=∠ACB,
∴∠EFC=∠ACB,
∴EF=EC,
∴DE=CE.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
