小学数学人教版四年级上4.1 三位数乘两位数课件(共51张PPT)
文档属性
| 名称 | 小学数学人教版四年级上4.1 三位数乘两位数课件(共51张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-03 15:19:12 | ||
图片预览










文档简介
(共51张PPT)
4
三位数乘两位数
4.1
因数的中间或末尾没有0的笔算乘法
学习目标
掌握三位数乘两位数的笔算乘法,并能正确地进行计算。
学习重难点
重点
理解并掌握三位数乘两位数的笔算方法。
难点
理解并掌握三位数乘两位数的笔算方法。
回顾复习
23×30=
47×20=
42×19≈
58×41≈
690
940
800
2400
1.
口算。
2.
计算。
1118
408
×
4
3
8
6
2
5
8
1
1
1
8
2
6
1
2
×
3
6
4
8
4
0
8
3
4
我是这样算的:先用第二个因数每一位上的数与第一个因数相乘,用哪一位上的数去乘,乘得的积的末位就和那一位对齐,再把两次乘得的积相加。
这是我们学过的两位数
乘两位数的乘法,该怎
样列竖式计算呢?
43×26=
12×34=
例题解读
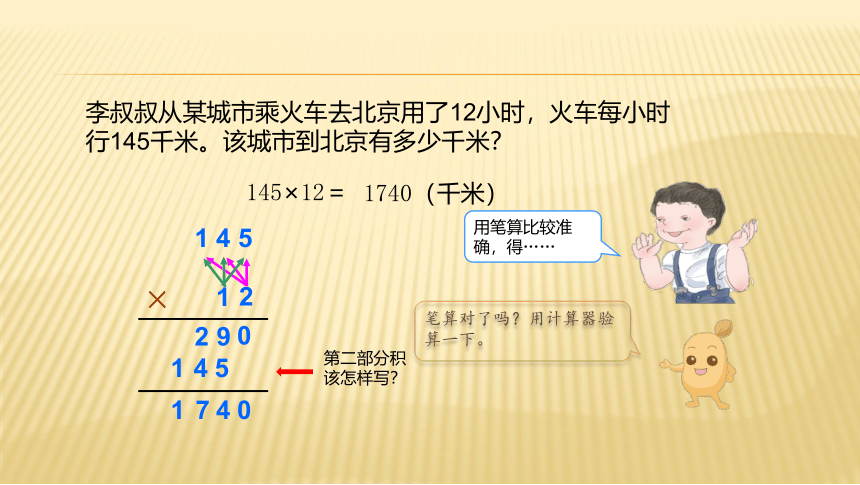
李叔叔从某城市乘火车去北京用了12小时,火车每小时行145千米。该城市到北京有多少千米?
同学们,题目中已知条件是
什么?要求的是什么?
已知火车1小时行145千米,行了
12小时,要求12小时行了多少千米?
例题解读
李叔叔从某城市乘火车去北京用了12小时,火车每小时行145千米。该城市到北京有多少千米?
怎么列式?
145×12=
那如何计算呢?
我是这样想的:
估计约有1450千米。
145×12≈1500
150
10
这样算准确吗?
1740(千米)
李叔叔从某城市乘火车去北京用了12小时,火车每小时行145千米。该城市到北京有多少千米?
145×12=
1
4
5
1
2
×
0
5
1
4
2
9
0
1
7
4
第二部分积
该怎样写?
用笔算比较准
确,得……
笔算对了吗?用计算器验算一下。
小结
三位数乘两位数的笔算方法
三位数乘两位数的计算方法:首先用两位数个位上的数去乘另一个因数,得数的末位和两位数的个位对齐;然后再用两位数十位上的数去乘另一个因数,得数的末位和两位数的十位对齐;最后把两次乘得的积加起来。
1.竖式计算。
134×12=
176×47=
×
2
4
7
1
7
6
4
2
1608
8272
3
1
2
0
7
7
2
8
×
8
1
2
1
3
4
4
8
6
2
3
1
0
6
1
随堂小测
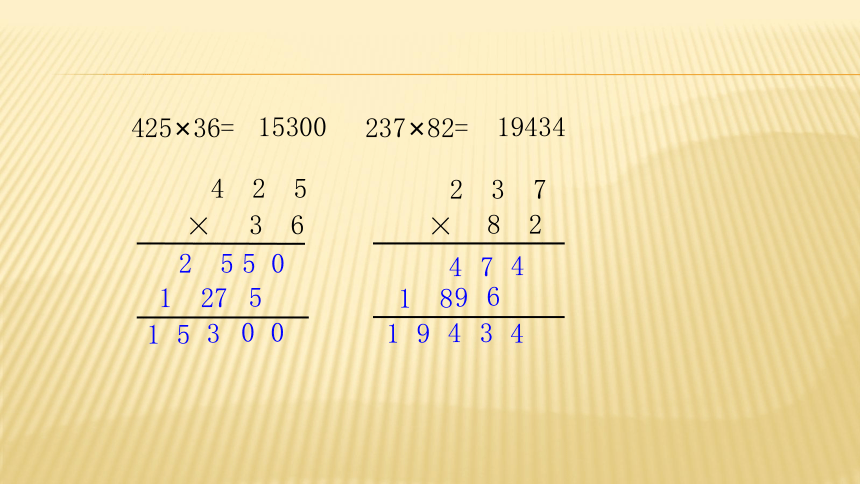
237×82=
425×36=
15300
19434
×
0
3
6
4
2
5
5
0
5
2
5
7
1
2
0
3
5
1
×
4
8
2
2
3
7
6
4
7
4
9
1
8
3
4
9
1
2.
学校要为各班新购买一套百科全书。
129元∕套
129×36=
4644(元)
答:购买这些新书一共要花4644元。
×
3
6
1
2
9
7
7
4
3
8
7
4
6
4
4
全校共36个班,购买这些
新书一共要花多少钱?
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
4
三位数乘两位数
4.2
因数的中间或末尾有0的笔算乘法
学习目标
掌握中间或末尾有0的三位数乘两位数的笔算方法。
学习重难点
重点
掌握中间或末尾有0的三位数乘两位数的笔算方法。
难点
因数末尾有0的竖式的简便计算方法、积末尾0的个数的确定。
回顾复习
1.
口算。
40×50=
12×30=
130×4=
80×70=
700×8=
2000
360
520
5600
5600
2.用竖式计算。
102×5= 140×7=
×
0
5
1
0
2
510
980
1
5
×
0
7
1
4
0
8
9
例题解读
(1)160×30=
______
两个因数的末尾都有零,
此题如何口算呢?
4800
先口算出16×3=48,再
在积的末尾添两个0。
可以这样想:
16×3=48,10×10=100
48×100=4800
所以160×30=4800
(1)160×30=
______
4800
8
1
6
0
×
3
0
先算16×3
4
再在积的末尾
添2个0
0
0
可以这样计算。
(1)160×30=
______
先口算出16×3=48,再
在积的末尾添两个0。
(2)106×30=
______
1
0
6
8
3
0
×
1
3
0
3
1
8
0
自己试一试!
小结
因数中间或末尾有0的乘法的笔算方法
(1)当三位数中间有0时,用第二个因数的个位、十位上的数依次去乘第一个因数的每一位数,包括0都要乘,0乘任何数都得0,有进位数时要加上进位的数。
(2)因数末尾有0的乘法,可以先把0前面的数相乘,然后看因数的末尾共有几个0,就在乘得的积的末尾添几个0。注意书写格式,末尾的0在一边,0前面的数要对齐。
随堂小测
2
2
0
×
4
0
0
0
8
8
1
6
0
×
6
0
0
0
9
6
3
6
0
×
2
5
0
0
2
0
1
8
7
9
0
5
8
0
×
1
2
6
0
8
6
1
1
5
6
9
240×22=
5280
2
4
0
×
2
2
4
8
4
8
5
2
8
0
305×50=
15250
3
0
5
5
0
×
1
5
2
5
0
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
4
三位数乘两位数
4.3
积的变化规律
学习目标
探索发现积的变化规律,能将这一规律灵活地运用于计算和解决问题中。
学习重难点
重点
掌握积的变化规律。
难点
能灵活地根据积的变化规律解决实际问题。
教材引入
学生完成下列两组计算:
6×2= 6×20= 6×200=
20×4=
10×4=
5×4=
12
120
1200
80
40
20
例题解读
6×2=
6×20=
6×200=
120
1200
(1)
12
10×4=
5×4=
80
40
20
20×4=
(2)
第(1)组题中,第2题同第1题比,因数是怎样变化的?积是怎样变化的?
一个因数不变,另一个
因数乘10,积也乘10。
观察下面两组题,说一说你发现了什么?
6×2=
6×20=
6×200=
120
1200
(1)
12
10×4=
5×4=
80
40
20
20×4=
(2)
第(1)组题中,第3题同第1题比,因数是怎样变化的?积是怎样变化的?
一个因数不变,另一个因数
乘100,积也乘100。
6×2=
6×20=
6×200=
120
1200
(1)
12
10×4=
5×4=
80
40
20
20×4=
(2)
第(2)组题中,第2题同第1题比,因数是怎样变化的?积是怎样变化的?
一个因数不变,另一个
因数除以2,积也除以2。
6×2=
6×20=
6×200=
120
1200
(1)
12
10×4=
5×4=
80
40
20
20×4=
(2)
第(2)组题中,第3题同第1题比,因数是怎样变化的?积是怎样变化的?
一个因数不变,另一个因数
除以4,积也除以4。
一个因数不变,另一个因数乘(或除以)几
(0除外),积也乘(或除以)几。
能举例说明你发现的
规律吗?
25×4=100
100×4=400
如果从下往上观察,第二
个因数没变,第一个因数
除以4,积也除以4。
我是这么举例的:
25×4=100
100×4=400
从上往下观察,第二个因数没变,第一个因数乘4,积也乘4。
小结
积的变化规律
一个因数不变,另一个因数乘几或除以几(0除外),积也乘(或除以)几。
1.先算出每组题中第1题的积,再写出下面两题的得数。
12×3=
120×3=
120×30=
48×5=
48×50=
48×500=
8×50=
8×25=
4×50=
36
360
3600
240
2400
24000
400
200
200
随堂小测
2.
扩大后的绿地面积是多少?
200平方米
8米
200平方米
8米
200平方米
8米
24米
24÷8=3
200×3=600(平方米)
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
4
三位数乘两位数
4.4
常见的两种数量关系
学习目标
1.掌握单价、数量和总价之间的关系。
2.会用复合单位表示速度,掌握速度、时间和路程之间的关系。
学习重难点
重点
运用两种常见的数量关系解决简单的实际问题。
难点
运用两种常见的数量关系解决简单的实际问题。
教材引入
为什么用乘法计算?
80×3=240(元)
解答下面的问题。
求3个80是多少。
(1)
篮球每个80元,买
3个要多少钱?
10×4=40(元)
(2)
鱼每千克10元,买
4千克要多少钱?
80×3=240(元)
1.解答下面的问题。
(1)
篮球每个80元,买
3个要多少钱?
在前面的学习中,我们经常会见到一些数量关系,下面我们就来总结两种常见的数量关系。
例题解读
这两个问题有什么共同点?
都是已知每件商品
的价钱。
还知道买了多少件
商品,最后算……
(2)
鱼每千克10元,买
4千克要多少钱?
80×3=240(元)
1.解答下面的问题。
(1)
篮球每个80元,买
3个要多少钱?
10×4=40(元)
例题解读
80×3=240(元)
10×4=40(元)
每件商品的价钱,叫做单价;
买了多少,叫做数量;
一共用的钱数,叫做总价。
单价
单价
…
…
数量
数量
…
…
总价
总价
…
…
你知道单价、数量与
总价之间的关系吗?
(2)
鱼每千克10元,买
4千克要多少钱?
1.解答下面的问题。
(1)
篮球每个80元,买
3个要多少钱?
单价×数量=总价
例题解读
(1)一辆汽车每小时行70千米,4小时行多少千米?
(2)一人骑自行车每分钟行225米,10分钟行多少千米?
70×4=280(千米)
225×10=2250(米)=2.25(千米)
2.解答下面的问题。
这两个问题有什么共同点?
都是知道每小时或
每分钟行的路程。
还知道行了几小时或几分钟,求一共行……
2.解答下面的问题。
(1)一辆汽车每小时行70千米,4小时行多少千米?
(2)一人骑自行车每分钟行225米,10分钟行多少千米?
70×4=280(千米)
225×10=2250(米)=2.25(千米)
一共行了多长的路,叫做路程;
每小时(或每分钟等)行的
路程,叫做速度;
行了几小时(或几分钟等),叫做时间。
上面汽车每小时行的路程叫做速度,可以写成70千米∕时,
读作70千米每时。
速度
…
时间
…
路程
…
2.解答下面的问题。
(1)一辆汽车每小时行70千米,4小时行多少千米?
(2)一人骑自行车每分钟行225米,10分钟行多少千米?
70×4=280(千米)
225×10=2250(米)=2.25(千米)
速度×时间=路程
你知道速度、时间与
路程之间的关系吗?
小结
单价、数量和总价的数量关系
速度、时间和路程的数量关系
单价×数量=总价
总价÷单价=数量
总价÷数量=单价
速度×时间=路程
路程÷速度=时间
路程÷时间=速度
随堂小测
1.不解答,只说出下面各题已知的是什么,要求的是什么。
(2)学校买了3台同样的复读机,花了420元,每台复读机多少元?
已知单价和数量,求总价。
已知数量和总价,求单价。
(1)每套校服120元,买5套要用多少钱?
2.不解答,只说出下面各题已知的是什么,要求的是什么。
(1)小林每分钟走60米,他15分钟走多少米?
(2)声音每秒传播340米,声音传播1700米要用多长时间?
已知速度和时间,求路程。
已知速度和路程,
求时间。
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
4
三位数乘两位数
4.1
因数的中间或末尾没有0的笔算乘法
学习目标
掌握三位数乘两位数的笔算乘法,并能正确地进行计算。
学习重难点
重点
理解并掌握三位数乘两位数的笔算方法。
难点
理解并掌握三位数乘两位数的笔算方法。
回顾复习
23×30=
47×20=
42×19≈
58×41≈
690
940
800
2400
1.
口算。
2.
计算。
1118
408
×
4
3
8
6
2
5
8
1
1
1
8
2
6
1
2
×
3
6
4
8
4
0
8
3
4
我是这样算的:先用第二个因数每一位上的数与第一个因数相乘,用哪一位上的数去乘,乘得的积的末位就和那一位对齐,再把两次乘得的积相加。
这是我们学过的两位数
乘两位数的乘法,该怎
样列竖式计算呢?
43×26=
12×34=
例题解读
李叔叔从某城市乘火车去北京用了12小时,火车每小时行145千米。该城市到北京有多少千米?
同学们,题目中已知条件是
什么?要求的是什么?
已知火车1小时行145千米,行了
12小时,要求12小时行了多少千米?
例题解读
李叔叔从某城市乘火车去北京用了12小时,火车每小时行145千米。该城市到北京有多少千米?
怎么列式?
145×12=
那如何计算呢?
我是这样想的:
估计约有1450千米。
145×12≈1500
150
10
这样算准确吗?
1740(千米)
李叔叔从某城市乘火车去北京用了12小时,火车每小时行145千米。该城市到北京有多少千米?
145×12=
1
4
5
1
2
×
0
5
1
4
2
9
0
1
7
4
第二部分积
该怎样写?
用笔算比较准
确,得……
笔算对了吗?用计算器验算一下。
小结
三位数乘两位数的笔算方法
三位数乘两位数的计算方法:首先用两位数个位上的数去乘另一个因数,得数的末位和两位数的个位对齐;然后再用两位数十位上的数去乘另一个因数,得数的末位和两位数的十位对齐;最后把两次乘得的积加起来。
1.竖式计算。
134×12=
176×47=
×
2
4
7
1
7
6
4
2
1608
8272
3
1
2
0
7
7
2
8
×
8
1
2
1
3
4
4
8
6
2
3
1
0
6
1
随堂小测
237×82=
425×36=
15300
19434
×
0
3
6
4
2
5
5
0
5
2
5
7
1
2
0
3
5
1
×
4
8
2
2
3
7
6
4
7
4
9
1
8
3
4
9
1
2.
学校要为各班新购买一套百科全书。
129元∕套
129×36=
4644(元)
答:购买这些新书一共要花4644元。
×
3
6
1
2
9
7
7
4
3
8
7
4
6
4
4
全校共36个班,购买这些
新书一共要花多少钱?
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
4
三位数乘两位数
4.2
因数的中间或末尾有0的笔算乘法
学习目标
掌握中间或末尾有0的三位数乘两位数的笔算方法。
学习重难点
重点
掌握中间或末尾有0的三位数乘两位数的笔算方法。
难点
因数末尾有0的竖式的简便计算方法、积末尾0的个数的确定。
回顾复习
1.
口算。
40×50=
12×30=
130×4=
80×70=
700×8=
2000
360
520
5600
5600
2.用竖式计算。
102×5= 140×7=
×
0
5
1
0
2
510
980
1
5
×
0
7
1
4
0
8
9
例题解读
(1)160×30=
______
两个因数的末尾都有零,
此题如何口算呢?
4800
先口算出16×3=48,再
在积的末尾添两个0。
可以这样想:
16×3=48,10×10=100
48×100=4800
所以160×30=4800
(1)160×30=
______
4800
8
1
6
0
×
3
0
先算16×3
4
再在积的末尾
添2个0
0
0
可以这样计算。
(1)160×30=
______
先口算出16×3=48,再
在积的末尾添两个0。
(2)106×30=
______
1
0
6
8
3
0
×
1
3
0
3
1
8
0
自己试一试!
小结
因数中间或末尾有0的乘法的笔算方法
(1)当三位数中间有0时,用第二个因数的个位、十位上的数依次去乘第一个因数的每一位数,包括0都要乘,0乘任何数都得0,有进位数时要加上进位的数。
(2)因数末尾有0的乘法,可以先把0前面的数相乘,然后看因数的末尾共有几个0,就在乘得的积的末尾添几个0。注意书写格式,末尾的0在一边,0前面的数要对齐。
随堂小测
2
2
0
×
4
0
0
0
8
8
1
6
0
×
6
0
0
0
9
6
3
6
0
×
2
5
0
0
2
0
1
8
7
9
0
5
8
0
×
1
2
6
0
8
6
1
1
5
6
9
240×22=
5280
2
4
0
×
2
2
4
8
4
8
5
2
8
0
305×50=
15250
3
0
5
5
0
×
1
5
2
5
0
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
4
三位数乘两位数
4.3
积的变化规律
学习目标
探索发现积的变化规律,能将这一规律灵活地运用于计算和解决问题中。
学习重难点
重点
掌握积的变化规律。
难点
能灵活地根据积的变化规律解决实际问题。
教材引入
学生完成下列两组计算:
6×2= 6×20= 6×200=
20×4=
10×4=
5×4=
12
120
1200
80
40
20
例题解读
6×2=
6×20=
6×200=
120
1200
(1)
12
10×4=
5×4=
80
40
20
20×4=
(2)
第(1)组题中,第2题同第1题比,因数是怎样变化的?积是怎样变化的?
一个因数不变,另一个
因数乘10,积也乘10。
观察下面两组题,说一说你发现了什么?
6×2=
6×20=
6×200=
120
1200
(1)
12
10×4=
5×4=
80
40
20
20×4=
(2)
第(1)组题中,第3题同第1题比,因数是怎样变化的?积是怎样变化的?
一个因数不变,另一个因数
乘100,积也乘100。
6×2=
6×20=
6×200=
120
1200
(1)
12
10×4=
5×4=
80
40
20
20×4=
(2)
第(2)组题中,第2题同第1题比,因数是怎样变化的?积是怎样变化的?
一个因数不变,另一个
因数除以2,积也除以2。
6×2=
6×20=
6×200=
120
1200
(1)
12
10×4=
5×4=
80
40
20
20×4=
(2)
第(2)组题中,第3题同第1题比,因数是怎样变化的?积是怎样变化的?
一个因数不变,另一个因数
除以4,积也除以4。
一个因数不变,另一个因数乘(或除以)几
(0除外),积也乘(或除以)几。
能举例说明你发现的
规律吗?
25×4=100
100×4=400
如果从下往上观察,第二
个因数没变,第一个因数
除以4,积也除以4。
我是这么举例的:
25×4=100
100×4=400
从上往下观察,第二个因数没变,第一个因数乘4,积也乘4。
小结
积的变化规律
一个因数不变,另一个因数乘几或除以几(0除外),积也乘(或除以)几。
1.先算出每组题中第1题的积,再写出下面两题的得数。
12×3=
120×3=
120×30=
48×5=
48×50=
48×500=
8×50=
8×25=
4×50=
36
360
3600
240
2400
24000
400
200
200
随堂小测
2.
扩大后的绿地面积是多少?
200平方米
8米
200平方米
8米
200平方米
8米
24米
24÷8=3
200×3=600(平方米)
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
4
三位数乘两位数
4.4
常见的两种数量关系
学习目标
1.掌握单价、数量和总价之间的关系。
2.会用复合单位表示速度,掌握速度、时间和路程之间的关系。
学习重难点
重点
运用两种常见的数量关系解决简单的实际问题。
难点
运用两种常见的数量关系解决简单的实际问题。
教材引入
为什么用乘法计算?
80×3=240(元)
解答下面的问题。
求3个80是多少。
(1)
篮球每个80元,买
3个要多少钱?
10×4=40(元)
(2)
鱼每千克10元,买
4千克要多少钱?
80×3=240(元)
1.解答下面的问题。
(1)
篮球每个80元,买
3个要多少钱?
在前面的学习中,我们经常会见到一些数量关系,下面我们就来总结两种常见的数量关系。
例题解读
这两个问题有什么共同点?
都是已知每件商品
的价钱。
还知道买了多少件
商品,最后算……
(2)
鱼每千克10元,买
4千克要多少钱?
80×3=240(元)
1.解答下面的问题。
(1)
篮球每个80元,买
3个要多少钱?
10×4=40(元)
例题解读
80×3=240(元)
10×4=40(元)
每件商品的价钱,叫做单价;
买了多少,叫做数量;
一共用的钱数,叫做总价。
单价
单价
…
…
数量
数量
…
…
总价
总价
…
…
你知道单价、数量与
总价之间的关系吗?
(2)
鱼每千克10元,买
4千克要多少钱?
1.解答下面的问题。
(1)
篮球每个80元,买
3个要多少钱?
单价×数量=总价
例题解读
(1)一辆汽车每小时行70千米,4小时行多少千米?
(2)一人骑自行车每分钟行225米,10分钟行多少千米?
70×4=280(千米)
225×10=2250(米)=2.25(千米)
2.解答下面的问题。
这两个问题有什么共同点?
都是知道每小时或
每分钟行的路程。
还知道行了几小时或几分钟,求一共行……
2.解答下面的问题。
(1)一辆汽车每小时行70千米,4小时行多少千米?
(2)一人骑自行车每分钟行225米,10分钟行多少千米?
70×4=280(千米)
225×10=2250(米)=2.25(千米)
一共行了多长的路,叫做路程;
每小时(或每分钟等)行的
路程,叫做速度;
行了几小时(或几分钟等),叫做时间。
上面汽车每小时行的路程叫做速度,可以写成70千米∕时,
读作70千米每时。
速度
…
时间
…
路程
…
2.解答下面的问题。
(1)一辆汽车每小时行70千米,4小时行多少千米?
(2)一人骑自行车每分钟行225米,10分钟行多少千米?
70×4=280(千米)
225×10=2250(米)=2.25(千米)
速度×时间=路程
你知道速度、时间与
路程之间的关系吗?
小结
单价、数量和总价的数量关系
速度、时间和路程的数量关系
单价×数量=总价
总价÷单价=数量
总价÷数量=单价
速度×时间=路程
路程÷速度=时间
路程÷时间=速度
随堂小测
1.不解答,只说出下面各题已知的是什么,要求的是什么。
(2)学校买了3台同样的复读机,花了420元,每台复读机多少元?
已知单价和数量,求总价。
已知数量和总价,求单价。
(1)每套校服120元,买5套要用多少钱?
2.不解答,只说出下面各题已知的是什么,要求的是什么。
(1)小林每分钟走60米,他15分钟走多少米?
(2)声音每秒传播340米,声音传播1700米要用多长时间?
已知速度和时间,求路程。
已知速度和路程,
求时间。
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
