11.1 与三角形有关的线段同步练习(含解析)
文档属性
| 名称 | 11.1 与三角形有关的线段同步练习(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 943.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-03 21:25:17 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版八年级上
11.1与三角形有关的线段同步练习
一.选择题
1.(2021春?沐川县期末)下列长度的各组线段不能组成一个三角形的是( )
A.2cm,2cm,1cm
B.2cm,2cm,2cm
C.2cm,2cm,3cm
D.2cm,2cm,4cm
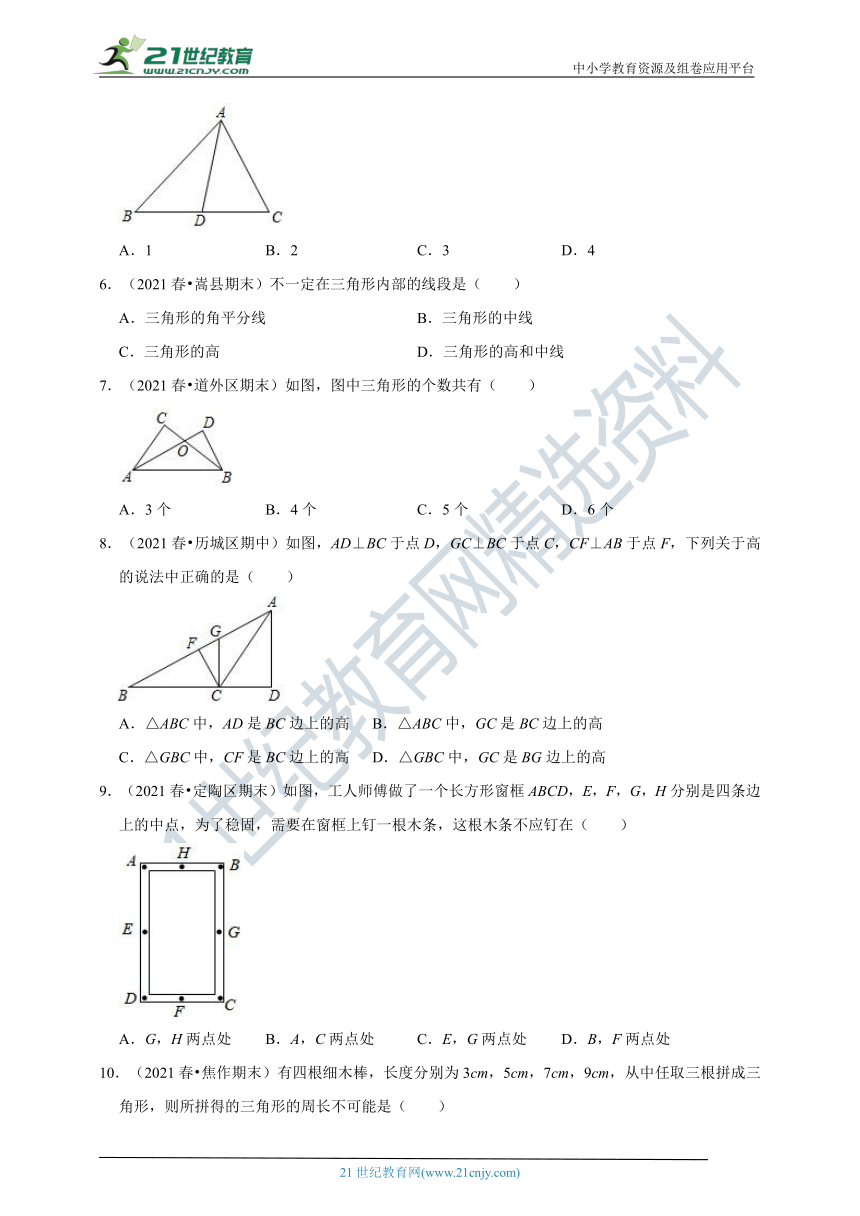
2.(2021春?长春期末)下列四个图中,正确画出△ABC中BC边上的高是( )
A.
B.
C.
D.
3.(2020秋?厦门期末)若AD是△ABC的中线,则下列结论正确的是( )
A.AD⊥BC
B.BD=CD
C.∠BAD=∠CAD
D.AD=BC
4.(2021春?宛城区期末)下列关于三角形的分类,正确的是( )
A.
B.
C.
D.
5.(2021春?青龙县期末)如图,在△ABC中,AB=10,AC=8,AD为中线,则△ABD与△ACD的周长之差为( )
A.1
B.2
C.3
D.4
6.(2021春?嵩县期末)不一定在三角形内部的线段是( )
A.三角形的角平分线
B.三角形的中线
C.三角形的高
D.三角形的高和中线
7.(2021春?道外区期末)如图,图中三角形的个数共有( )
A.3个
B.4个
C.5个
D.6个
8.(2021春?历城区期中)如图,AD⊥BC于点D,GC⊥BC于点C,CF⊥AB于点F,下列关于高的说法中正确的是( )
A.△ABC中,AD是BC边上的高
B.△ABC中,GC是BC边上的高
C.△GBC中,CF是BC边上的高
D.△GBC中,GC是BG边上的高
9.(2021春?定陶区期末)如图,工人师傅做了一个长方形窗框ABCD,E,F,G,H分别是四条边上的中点,为了稳固,需要在窗框上钉一根木条,这根木条不应钉在( )
A.G,H两点处
B.A,C两点处
C.E,G两点处
D.B,F两点处
10.(2021春?焦作期末)有四根细木棒,长度分别为3cm,5cm,7cm,9cm,从中任取三根拼成三角形,则所拼得的三角形的周长不可能是( )
A.21cm
B.17cm
C.19cm
D.15cm
二.填空题
11.(2021春?项城市期末)射击队员在瞄准目标时,手、肘、肩构成托枪三角形,说明三角形具有
.
12.(2021春?朝阳区校级期末)已知三角形的两边长分别为2和4,第三边长为整数,则该三角形的周长最大值为
.
13.(2021春?九江期末)小明现有两根4cm、9cm的木棒,他想以这两根木棒为边钉一个三角形木框,现从5cm,7cm,9cm,11cm,13cm,17cm的木棒中选择第三根(木棒不能折断),则小明有
种选择方案.
14.(2019秋?潮南区期中)若△ABC中,∠ACB是钝角,AD是BC边上的高,若AD=2,BD=3.CD=1,则△ABC的面积等于
.
15.(2021春?夏津县期末)已知a,b,c是三角形的三边长,化简:|a﹣b﹣c|+|b﹣c+a|﹣|c﹣a﹣b|=
.
16.(2021春?庐山市
期末)在一个三角形中,如果有一条边的长是另一条边长的2倍,且有两条边的和是另一条边的2倍,那么我们就把这样的三角形叫2倍边三角形.如果一个2倍边三角形中有一条边长为6,则这个三角形的另外两条边的和可以是
.
三.解答题
17.(2021春?靖江市月考)如图,在三角形ABC中,AB=10cm,AC=6cm,D是BC的中点,E点在边AB上.
(1)若三角形BDE的周长与四边形ACDE的周长相等,求线段AE的长.
(2)若三角形ABC的周长被DE分成的两部分的差是2cm,求线段AE的长.
18.(2020秋?恩施市月考)已知a、b、c是△ABC的三边长,化简|a+b﹣c|+|b﹣a﹣c|﹣|c﹣a+b|.
19.(2020秋?安庆期中)已知:如图,点D是△ABC内一点.
求证:
(1)BD+CD<AB+AC;
(2)AD+BD+CD<AB+BC+AC.
20.(2020秋?开州区校级月考)小刚准备用一段长50米的篱笆围成一个三角形形状的场地,用于饲养鸡,已知第一条边长为m米,由于条件限制第二条边长只能比第一条边长的3倍少2米.
①用含m的式子表示第三条边长;
②第一条边长能否为10米?为什么?
③若第一条边长最短,求m的取值范围.
答案与解析
一.选择题
1.(2021春?沐川县期末)下列长度的各组线段不能组成一个三角形的是( )
A.2cm,2cm,1cm
B.2cm,2cm,2cm
C.2cm,2cm,3cm
D.2cm,2cm,4cm
【解析】解:A、∵2+1>2,∴能组成三角形;
B、∵2+2>2,∴能组成三角形;
C、∵2+2>3,∴能组成三角形;
D、∵2+2=4,∴不能组成三角形.
故选:D.
2.(2021春?长春期末)下列四个图中,正确画出△ABC中BC边上的高是( )
A.
B.
C.
D.
【解析】解:根据三角形高线的定义,BC边上的高是过点A向BC作垂线垂足为D,
纵观各图形,选项ABD都不符合题意,选项C符合题意.
故选:C.
3.(2020秋?厦门期末)若AD是△ABC的中线,则下列结论正确的是( )
A.AD⊥BC
B.BD=CD
C.∠BAD=∠CAD
D.AD=BC
【解析】解:∵AD是△ABC的中线,
∴BD=DC,
故选:B.
4.(2021春?宛城区期末)下列关于三角形的分类,正确的是( )
A.
B.
C.
D.
【解析】解:A、等腰直角三角形应该是直角三角形,不符合题意;
B、该选项中的三角形的分类正确,符合题意;
C、等腰三角形包括等边三角形,不符合题意;
D、等腰三角形包括等边三角形,不符合题意;
故选:B.
5.(2021春?青龙县期末)如图,在△ABC中,AB=10,AC=8,AD为中线,则△ABD与△ACD的周长之差为( )
A.1
B.2
C.3
D.4
【解析】解:∵AD是△ABC中BC边上的中线,
∴BD=DC=BC,
∴△ABD与△ACD的周长之差
=(AB+BD+AD)﹣(AC+DC+AD)
=AB﹣AC
=10﹣8
=2.
则△ABD与△ACD的周长之差=2.
故选:B.
6.(2021春?嵩县期末)不一定在三角形内部的线段是( )
A.三角形的角平分线
B.三角形的中线
C.三角形的高
D.三角形的高和中线
【解析】解:因为在三角形中,
它的中线、角平分线一定在三角形的内部,
而钝角三角形的两条高在三角形的外部.
故选:C.
7.(2021春?道外区期末)如图,图中三角形的个数共有( )
A.3个
B.4个
C.5个
D.6个
【解析】解:图中是三角形的有:△AOC、△BOD、△AOB、△ABC、△ABD.
故选:C.
8.(2021春?历城区期中)如图,AD⊥BC于点D,GC⊥BC于点C,CF⊥AB于点F,下列关于高的说法中正确的是( )
A.△ABC中,AD是BC边上的高
B.△ABC中,GC是BC边上的高
C.△GBC中,CF是BC边上的高
D.△GBC中,GC是BG边上的高
【解析】解:∵AD⊥BC于点D,
∴△ABC中,AD是BC边上的高,故A选项正确,B选项错误;
∵CF⊥AB于点F,
∴△GBC中,CF是BG边上的高,故C选项错误,D选项错误.
故选:A.
9.(2021春?定陶区期末)如图,工人师傅做了一个长方形窗框ABCD,E,F,G,H分别是四条边上的中点,为了稳固,需要在窗框上钉一根木条,这根木条不应钉在( )
A.G,H两点处
B.A,C两点处
C.E,G两点处
D.B,F两点处
【解析】解:工人师傅做了一个长方形窗框ABCD,工人师傅为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在E、G两点之间(没有构成三角形),这种做法根据的是三角形的稳定性.
故选:C.
10.(2021春?焦作期末)有四根细木棒,长度分别为3cm,5cm,7cm,9cm,从中任取三根拼成三角形,则所拼得的三角形的周长不可能是( )
A.21cm
B.17cm
C.19cm
D.15cm
【解析】解:从四根细木棒中随机抽出三根木棒,所有结果为3、5、7;3、5、9;3、7、9;5、7、9,
∵3+5>7;3+5<9;3+7>9;5+7>9;
故①3、5、7;②3、7、9;③5、7、9,可以围成的三角形共有3种,
周长分别为15cm,19cm,21cm,只有17cm不适合,
故选:B.
二.填空题
11.(2021春?项城市期末)射击队员在瞄准目标时,手、肘、肩构成托枪三角形,说明三角形具有
稳定性 .
【解析】解:射击队员在瞄准目标时,手、肘、肩构成托枪三角形,说明三角形具有稳定性,
故答案为:稳定性.
12.(2021春?朝阳区校级期末)已知三角形的两边长分别为2和4,第三边长为整数,则该三角形的周长最大值为
11 .
【解析】解:设第三边为a,
根据三角形的三边关系,得:4﹣2<a<2+4,
即2<a<6,
∵a为整数,
∴a的最大整数值为5,
则三角形的最大周长为2+4+5=11.
故答案为:11.
13.(2021春?九江期末)小明现有两根4cm、9cm的木棒,他想以这两根木棒为边钉一个三角形木框,现从5cm,7cm,9cm,11cm,13cm,17cm的木棒中选择第三根(木棒不能折断),则小明有
三 种选择方案.
【解析】解:根据三角形的三边关系,得:第三根木棒应>5cm,而<13cm.故7cm,9cm,11cm能满足,有三种选择方案.
故答案是:三.
14.(2019秋?潮南区期中)若△ABC中,∠ACB是钝角,AD是BC边上的高,若AD=2,BD=3.CD=1,则△ABC的面积等于 2 .
【解析】解:如图.
∵BD=3,CD=1,
∴BC=BD﹣CD=2,
又∵AD是BC边上的高,AD=2,
∴△ABC的面积=BC?AD=×2×2=2.
故答案为2.
15.(2021春?夏津县期末)已知a,b,c是三角形的三边长,化简:|a﹣b﹣c|+|b﹣c+a|﹣|c﹣a﹣b|= ﹣a+b+c .
【解析】解:∵a、b、c是三角形的三边长,
∴a+b>c,b+c>a,a+b>c,
∴a﹣b﹣c<0,b﹣c+a>0,c﹣a﹣b<0,
∴|a﹣b﹣c|+|b﹣c+a|﹣|c﹣a﹣b|=﹣a+b+c+b﹣c+a+c﹣a﹣b=﹣a+b+c.
故答案为:﹣a+b+c.
16.(2021春?庐山市
期末)在一个三角形中,如果有一条边的长是另一条边长的2倍,且有两条边的和是另一条边的2倍,那么我们就把这样的三角形叫2倍边三角形.如果一个2倍边三角形中有一条边长为6,则这个三角形的另外两条边的和可以是
12,9或3,4.5或4,8 .
【解析】解:设最短边为x,其他两边分别为2x,1.5x,
当x=6时,其他两边为12,9,因为6+9>12,符合题意;
当2x=6时,其他两边为3,4.5,因为3+4.5>6,符合题意;
当1.5x=6时,其他两边为4,8,因为4+6>8,符合题意;
故答案为:12,9或3,4.5或4,8.
三.解答题
17.(2021春?靖江市月考)如图,在三角形ABC中,AB=10cm,AC=6cm,D是BC的中点,E点在边AB上.
(1)若三角形BDE的周长与四边形ACDE的周长相等,求线段AE的长.
(2)若三角形ABC的周长被DE分成的两部分的差是2cm,求线段AE的长.
【解析】解:(1)由图可知三角形BDE的周长=BE+BD+DE,四边形ACDE的周长=AE+AC+DC+DE,
又三角形BDE的周长与四边形ACDE的周长相等,D为BC中点,
∴BD=DC,BE+BD+DE=AE+AC+DC+DE,
即BE=AE+AC,
∵AB=10cm,AC=6cm,
∴10﹣AE=AE+6,
∴AE=2cm.
(2)由三角形ABC的周长被DE分成的两部分的差是2,可得方程
①BE=AE+AC+2或②BE=AE+AC﹣2.
解①得AE=1cm,解②得AE=3cm.
故AE长为1cm或3cm.
18.(2020秋?恩施市月考)已知a、b、c是△ABC的三边长,化简|a+b﹣c|+|b﹣a﹣c|﹣|c﹣a+b|.
【解析】解:由三角形三边关系可得:a+b>c,b<a+c,c+b>a,
∴a+b﹣c>0,b﹣a﹣c<0,c﹣a+b>0,
∴原式=a+b﹣c﹣b+a+c﹣c+a﹣b
=3a﹣b﹣c.
19.(2020秋?安庆期中)已知:如图,点D是△ABC内一点.
求证:
(1)BD+CD<AB+AC;
(2)AD+BD+CD<AB+BC+AC.
【解析】证明:(1)延长BD交AC于E,
在△ABE中,有AB+AE>BE,
在△EDC中,有ED+EC>CD,
∴AB+AE+ED+EC>BE+CD,
∵AE+EC=AC,BE=BD+DE,
∴AB+AC+ED>BD+DE+CD,
∴AB+AC>BD+CD;
(2)由(1)同理可得:
AB+BC>AD+CD,
BC+AC>BD+AD,
AB+AC>BD+CD,
∴2(AB+BC+AC)>2(AD+BD+CD),
∴AB+BC+AC>AD+BD+CD.
20.(2020秋?开州区校级月考)小刚准备用一段长50米的篱笆围成一个三角形形状的场地,用于饲养鸡,已知第一条边长为m米,由于条件限制第二条边长只能比第一条边长的3倍少2米.
①用含m的式子表示第三条边长;
②第一条边长能否为10米?为什么?
③若第一条边长最短,求m的取值范围.
【解析】解:(1)∵第二条边长为(3m﹣2)米,
∴第三条边长为50﹣m﹣(3m﹣2)=(52﹣4m)米;
(2)当m=10时,三边长分别为10,28,12,
由于10+12<28,所以不能构成三角形,即第一条边长不能为10米;
(3)由题意,得,
解得<m<9.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
人教版八年级上
11.1与三角形有关的线段同步练习
一.选择题
1.(2021春?沐川县期末)下列长度的各组线段不能组成一个三角形的是( )
A.2cm,2cm,1cm
B.2cm,2cm,2cm
C.2cm,2cm,3cm
D.2cm,2cm,4cm
2.(2021春?长春期末)下列四个图中,正确画出△ABC中BC边上的高是( )
A.
B.
C.
D.
3.(2020秋?厦门期末)若AD是△ABC的中线,则下列结论正确的是( )
A.AD⊥BC
B.BD=CD
C.∠BAD=∠CAD
D.AD=BC
4.(2021春?宛城区期末)下列关于三角形的分类,正确的是( )
A.
B.
C.
D.
5.(2021春?青龙县期末)如图,在△ABC中,AB=10,AC=8,AD为中线,则△ABD与△ACD的周长之差为( )
A.1
B.2
C.3
D.4
6.(2021春?嵩县期末)不一定在三角形内部的线段是( )
A.三角形的角平分线
B.三角形的中线
C.三角形的高
D.三角形的高和中线
7.(2021春?道外区期末)如图,图中三角形的个数共有( )
A.3个
B.4个
C.5个
D.6个
8.(2021春?历城区期中)如图,AD⊥BC于点D,GC⊥BC于点C,CF⊥AB于点F,下列关于高的说法中正确的是( )
A.△ABC中,AD是BC边上的高
B.△ABC中,GC是BC边上的高
C.△GBC中,CF是BC边上的高
D.△GBC中,GC是BG边上的高
9.(2021春?定陶区期末)如图,工人师傅做了一个长方形窗框ABCD,E,F,G,H分别是四条边上的中点,为了稳固,需要在窗框上钉一根木条,这根木条不应钉在( )
A.G,H两点处
B.A,C两点处
C.E,G两点处
D.B,F两点处
10.(2021春?焦作期末)有四根细木棒,长度分别为3cm,5cm,7cm,9cm,从中任取三根拼成三角形,则所拼得的三角形的周长不可能是( )
A.21cm
B.17cm
C.19cm
D.15cm
二.填空题
11.(2021春?项城市期末)射击队员在瞄准目标时,手、肘、肩构成托枪三角形,说明三角形具有
.
12.(2021春?朝阳区校级期末)已知三角形的两边长分别为2和4,第三边长为整数,则该三角形的周长最大值为
.
13.(2021春?九江期末)小明现有两根4cm、9cm的木棒,他想以这两根木棒为边钉一个三角形木框,现从5cm,7cm,9cm,11cm,13cm,17cm的木棒中选择第三根(木棒不能折断),则小明有
种选择方案.
14.(2019秋?潮南区期中)若△ABC中,∠ACB是钝角,AD是BC边上的高,若AD=2,BD=3.CD=1,则△ABC的面积等于
.
15.(2021春?夏津县期末)已知a,b,c是三角形的三边长,化简:|a﹣b﹣c|+|b﹣c+a|﹣|c﹣a﹣b|=
.
16.(2021春?庐山市
期末)在一个三角形中,如果有一条边的长是另一条边长的2倍,且有两条边的和是另一条边的2倍,那么我们就把这样的三角形叫2倍边三角形.如果一个2倍边三角形中有一条边长为6,则这个三角形的另外两条边的和可以是
.
三.解答题
17.(2021春?靖江市月考)如图,在三角形ABC中,AB=10cm,AC=6cm,D是BC的中点,E点在边AB上.
(1)若三角形BDE的周长与四边形ACDE的周长相等,求线段AE的长.
(2)若三角形ABC的周长被DE分成的两部分的差是2cm,求线段AE的长.
18.(2020秋?恩施市月考)已知a、b、c是△ABC的三边长,化简|a+b﹣c|+|b﹣a﹣c|﹣|c﹣a+b|.
19.(2020秋?安庆期中)已知:如图,点D是△ABC内一点.
求证:
(1)BD+CD<AB+AC;
(2)AD+BD+CD<AB+BC+AC.
20.(2020秋?开州区校级月考)小刚准备用一段长50米的篱笆围成一个三角形形状的场地,用于饲养鸡,已知第一条边长为m米,由于条件限制第二条边长只能比第一条边长的3倍少2米.
①用含m的式子表示第三条边长;
②第一条边长能否为10米?为什么?
③若第一条边长最短,求m的取值范围.
答案与解析
一.选择题
1.(2021春?沐川县期末)下列长度的各组线段不能组成一个三角形的是( )
A.2cm,2cm,1cm
B.2cm,2cm,2cm
C.2cm,2cm,3cm
D.2cm,2cm,4cm
【解析】解:A、∵2+1>2,∴能组成三角形;
B、∵2+2>2,∴能组成三角形;
C、∵2+2>3,∴能组成三角形;
D、∵2+2=4,∴不能组成三角形.
故选:D.
2.(2021春?长春期末)下列四个图中,正确画出△ABC中BC边上的高是( )
A.
B.
C.
D.
【解析】解:根据三角形高线的定义,BC边上的高是过点A向BC作垂线垂足为D,
纵观各图形,选项ABD都不符合题意,选项C符合题意.
故选:C.
3.(2020秋?厦门期末)若AD是△ABC的中线,则下列结论正确的是( )
A.AD⊥BC
B.BD=CD
C.∠BAD=∠CAD
D.AD=BC
【解析】解:∵AD是△ABC的中线,
∴BD=DC,
故选:B.
4.(2021春?宛城区期末)下列关于三角形的分类,正确的是( )
A.
B.
C.
D.
【解析】解:A、等腰直角三角形应该是直角三角形,不符合题意;
B、该选项中的三角形的分类正确,符合题意;
C、等腰三角形包括等边三角形,不符合题意;
D、等腰三角形包括等边三角形,不符合题意;
故选:B.
5.(2021春?青龙县期末)如图,在△ABC中,AB=10,AC=8,AD为中线,则△ABD与△ACD的周长之差为( )
A.1
B.2
C.3
D.4
【解析】解:∵AD是△ABC中BC边上的中线,
∴BD=DC=BC,
∴△ABD与△ACD的周长之差
=(AB+BD+AD)﹣(AC+DC+AD)
=AB﹣AC
=10﹣8
=2.
则△ABD与△ACD的周长之差=2.
故选:B.
6.(2021春?嵩县期末)不一定在三角形内部的线段是( )
A.三角形的角平分线
B.三角形的中线
C.三角形的高
D.三角形的高和中线
【解析】解:因为在三角形中,
它的中线、角平分线一定在三角形的内部,
而钝角三角形的两条高在三角形的外部.
故选:C.
7.(2021春?道外区期末)如图,图中三角形的个数共有( )
A.3个
B.4个
C.5个
D.6个
【解析】解:图中是三角形的有:△AOC、△BOD、△AOB、△ABC、△ABD.
故选:C.
8.(2021春?历城区期中)如图,AD⊥BC于点D,GC⊥BC于点C,CF⊥AB于点F,下列关于高的说法中正确的是( )
A.△ABC中,AD是BC边上的高
B.△ABC中,GC是BC边上的高
C.△GBC中,CF是BC边上的高
D.△GBC中,GC是BG边上的高
【解析】解:∵AD⊥BC于点D,
∴△ABC中,AD是BC边上的高,故A选项正确,B选项错误;
∵CF⊥AB于点F,
∴△GBC中,CF是BG边上的高,故C选项错误,D选项错误.
故选:A.
9.(2021春?定陶区期末)如图,工人师傅做了一个长方形窗框ABCD,E,F,G,H分别是四条边上的中点,为了稳固,需要在窗框上钉一根木条,这根木条不应钉在( )
A.G,H两点处
B.A,C两点处
C.E,G两点处
D.B,F两点处
【解析】解:工人师傅做了一个长方形窗框ABCD,工人师傅为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在E、G两点之间(没有构成三角形),这种做法根据的是三角形的稳定性.
故选:C.
10.(2021春?焦作期末)有四根细木棒,长度分别为3cm,5cm,7cm,9cm,从中任取三根拼成三角形,则所拼得的三角形的周长不可能是( )
A.21cm
B.17cm
C.19cm
D.15cm
【解析】解:从四根细木棒中随机抽出三根木棒,所有结果为3、5、7;3、5、9;3、7、9;5、7、9,
∵3+5>7;3+5<9;3+7>9;5+7>9;
故①3、5、7;②3、7、9;③5、7、9,可以围成的三角形共有3种,
周长分别为15cm,19cm,21cm,只有17cm不适合,
故选:B.
二.填空题
11.(2021春?项城市期末)射击队员在瞄准目标时,手、肘、肩构成托枪三角形,说明三角形具有
稳定性 .
【解析】解:射击队员在瞄准目标时,手、肘、肩构成托枪三角形,说明三角形具有稳定性,
故答案为:稳定性.
12.(2021春?朝阳区校级期末)已知三角形的两边长分别为2和4,第三边长为整数,则该三角形的周长最大值为
11 .
【解析】解:设第三边为a,
根据三角形的三边关系,得:4﹣2<a<2+4,
即2<a<6,
∵a为整数,
∴a的最大整数值为5,
则三角形的最大周长为2+4+5=11.
故答案为:11.
13.(2021春?九江期末)小明现有两根4cm、9cm的木棒,他想以这两根木棒为边钉一个三角形木框,现从5cm,7cm,9cm,11cm,13cm,17cm的木棒中选择第三根(木棒不能折断),则小明有
三 种选择方案.
【解析】解:根据三角形的三边关系,得:第三根木棒应>5cm,而<13cm.故7cm,9cm,11cm能满足,有三种选择方案.
故答案是:三.
14.(2019秋?潮南区期中)若△ABC中,∠ACB是钝角,AD是BC边上的高,若AD=2,BD=3.CD=1,则△ABC的面积等于 2 .
【解析】解:如图.
∵BD=3,CD=1,
∴BC=BD﹣CD=2,
又∵AD是BC边上的高,AD=2,
∴△ABC的面积=BC?AD=×2×2=2.
故答案为2.
15.(2021春?夏津县期末)已知a,b,c是三角形的三边长,化简:|a﹣b﹣c|+|b﹣c+a|﹣|c﹣a﹣b|= ﹣a+b+c .
【解析】解:∵a、b、c是三角形的三边长,
∴a+b>c,b+c>a,a+b>c,
∴a﹣b﹣c<0,b﹣c+a>0,c﹣a﹣b<0,
∴|a﹣b﹣c|+|b﹣c+a|﹣|c﹣a﹣b|=﹣a+b+c+b﹣c+a+c﹣a﹣b=﹣a+b+c.
故答案为:﹣a+b+c.
16.(2021春?庐山市
期末)在一个三角形中,如果有一条边的长是另一条边长的2倍,且有两条边的和是另一条边的2倍,那么我们就把这样的三角形叫2倍边三角形.如果一个2倍边三角形中有一条边长为6,则这个三角形的另外两条边的和可以是
12,9或3,4.5或4,8 .
【解析】解:设最短边为x,其他两边分别为2x,1.5x,
当x=6时,其他两边为12,9,因为6+9>12,符合题意;
当2x=6时,其他两边为3,4.5,因为3+4.5>6,符合题意;
当1.5x=6时,其他两边为4,8,因为4+6>8,符合题意;
故答案为:12,9或3,4.5或4,8.
三.解答题
17.(2021春?靖江市月考)如图,在三角形ABC中,AB=10cm,AC=6cm,D是BC的中点,E点在边AB上.
(1)若三角形BDE的周长与四边形ACDE的周长相等,求线段AE的长.
(2)若三角形ABC的周长被DE分成的两部分的差是2cm,求线段AE的长.
【解析】解:(1)由图可知三角形BDE的周长=BE+BD+DE,四边形ACDE的周长=AE+AC+DC+DE,
又三角形BDE的周长与四边形ACDE的周长相等,D为BC中点,
∴BD=DC,BE+BD+DE=AE+AC+DC+DE,
即BE=AE+AC,
∵AB=10cm,AC=6cm,
∴10﹣AE=AE+6,
∴AE=2cm.
(2)由三角形ABC的周长被DE分成的两部分的差是2,可得方程
①BE=AE+AC+2或②BE=AE+AC﹣2.
解①得AE=1cm,解②得AE=3cm.
故AE长为1cm或3cm.
18.(2020秋?恩施市月考)已知a、b、c是△ABC的三边长,化简|a+b﹣c|+|b﹣a﹣c|﹣|c﹣a+b|.
【解析】解:由三角形三边关系可得:a+b>c,b<a+c,c+b>a,
∴a+b﹣c>0,b﹣a﹣c<0,c﹣a+b>0,
∴原式=a+b﹣c﹣b+a+c﹣c+a﹣b
=3a﹣b﹣c.
19.(2020秋?安庆期中)已知:如图,点D是△ABC内一点.
求证:
(1)BD+CD<AB+AC;
(2)AD+BD+CD<AB+BC+AC.
【解析】证明:(1)延长BD交AC于E,
在△ABE中,有AB+AE>BE,
在△EDC中,有ED+EC>CD,
∴AB+AE+ED+EC>BE+CD,
∵AE+EC=AC,BE=BD+DE,
∴AB+AC+ED>BD+DE+CD,
∴AB+AC>BD+CD;
(2)由(1)同理可得:
AB+BC>AD+CD,
BC+AC>BD+AD,
AB+AC>BD+CD,
∴2(AB+BC+AC)>2(AD+BD+CD),
∴AB+BC+AC>AD+BD+CD.
20.(2020秋?开州区校级月考)小刚准备用一段长50米的篱笆围成一个三角形形状的场地,用于饲养鸡,已知第一条边长为m米,由于条件限制第二条边长只能比第一条边长的3倍少2米.
①用含m的式子表示第三条边长;
②第一条边长能否为10米?为什么?
③若第一条边长最短,求m的取值范围.
【解析】解:(1)∵第二条边长为(3m﹣2)米,
∴第三条边长为50﹣m﹣(3m﹣2)=(52﹣4m)米;
(2)当m=10时,三边长分别为10,28,12,
由于10+12<28,所以不能构成三角形,即第一条边长不能为10米;
(3)由题意,得,
解得<m<9.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
