11.2 与三角形有关的角同步练习(含解析)
文档属性
| 名称 | 11.2 与三角形有关的角同步练习(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-03 21:27:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版八年级上
11.2与三角形有关的角同步练习
一.选择题
1.(2021春?历下区期中)在下列条件:①∠A+∠B=∠C,②∠A:∠B:∠C=5:3:2,③∠A=90°﹣∠B,④∠A=2∠B=3∠C中,能确定△ABC是直角三角形的条件有( )
A.1个
B.2个
C.3个
D.4个
2.(2021春?娄星区校级期中)已知在Rt△ABC中,∠B=90°,∠C=35°,则∠A等于( )
A.35°
B.45°
C.55°
D.65°
3.(2021?河池)如图,∠A=40°,∠CBD是△ABC的外角,∠CBD=120°,则∠C的大小是( )
A.90°
B.80°
C.60°
D.40°
4.(2021?平谷区一模)如图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D,则下列结论不一定成立的是( )
A.∠1+∠2=90°
B.∠2=∠3
C.∠1=∠4
D.∠1=30°
5.(2020秋?芜湖期中)如图,△ABC中,∠A=20°,沿BE将此三角形对折,又沿BA′再一次对折,点C落在BE上的C′处,此时∠C′DB=74°,则原三角形的∠C的度数为( )
A.27°
B.59°
C.69°
D.79°
6.(2020春?石狮市期末)在直角三角形ABC中,∠A:∠B:∠C=2:m:4,则m的值是( )
A.3
B.4
C.2或6
D.2或4
7.(2021春?永年区期末)如图,BF是∠ABD的平分线,CE是∠ACD的平分线,BF与CE交于点G,若∠BDC=140°,∠BGC=110°,则∠A的度数为( )
A.50°
B.55°
C.70°
D.80°
8.(2021春?建平县期末)定义:当三角形中一个内角α是另一个内角的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的一个内角为48°,那么这个“特征角”α的度数为( )
A.48°
B.96°
C.88°或48°
D.48°或96°或88°
9.(2021春?闵行区校级月考)下列说法中错误的是( )
A.三角形的三个内角中,最多有一个钝角
B.三角形三个内角中,至少有两个锐角
C.直角三角形中有两个锐角互余
D.三角形中两个内角和必大于90°
10.(2021春?周村区月考)如图,在△CEF中,∠E=80°,∠F=55°,AB∥CF,AD∥CE,连接BC,CD,则∠A的度数是( )
A.45°
B.50°
C.55°
D.80°
二.填空题
11.(2021春?铁西区期中)在△ABC中,∠A:∠B:∠C=4:4:7,则∠C的度数为
°.
12.(2021春?乐清市期末)如图,直线a,b所成的角跑到画板外面了,某同学发现只要量出一条直线分别与直线a,b相交所形成的角的度数就可求得该角,已知∠1=71°,∠2=78°,则直线a,b所形成的角的度数为
°.
13.(2020秋?前郭县期末)如图,C岛在A岛的北偏东45°方向,在B岛的北偏西25°方向,则∠ACB=
°.
14.(2021春?沙坪坝区校级期中)如图,在Rt△ABC中,∠B=90°,∠A=60°.将三角形沿EF翻折,使点C与边AB上的D点重合.若∠EFD=2∠AED,则∠AED的度数为
.
15.(2021春?泌阳县期末)在三角形的所有外角(每个顶点处只取一个外角)中,锐角最多有
个.
16.(2021春?江汉区期末)在△ABC中,∠BAC=50°,BE、CF是△ABC的高,直线BE、CF交于点H,则∠BHC的度数是
.
三.解答题
17.(2021春?望城区期末)如图,在△ABC
中,∠B=40°,∠C=110°.
(1)画出下列图形:
①BC边上的高AD;
②∠A的角平分线AE.
(2)试求∠DAE的度数.
18.(2021春?淮阳区校级期末)如图,已知CD是△ABC中∠ACB的外角平分线.
(1)若∠ACE=150°,∠BAC=100°,求∠B的大小;
(2)请说明∠BAC>∠B.
19.(2021春?长春期末)[规律探索]探索三角形的内(外)角平分线形成的角的规律:
在三角形中,由三角形的内角平分线外角平分线所形成的角存在一定的规律.
规律1:三角形的两个内角的平分线形成的钝角等于90°加上第三个内角度数的一半;
规律2:三角形的两个外角的平分线形成的锐角等于90°减去与这两个外角不相邻的内角度数的一半.
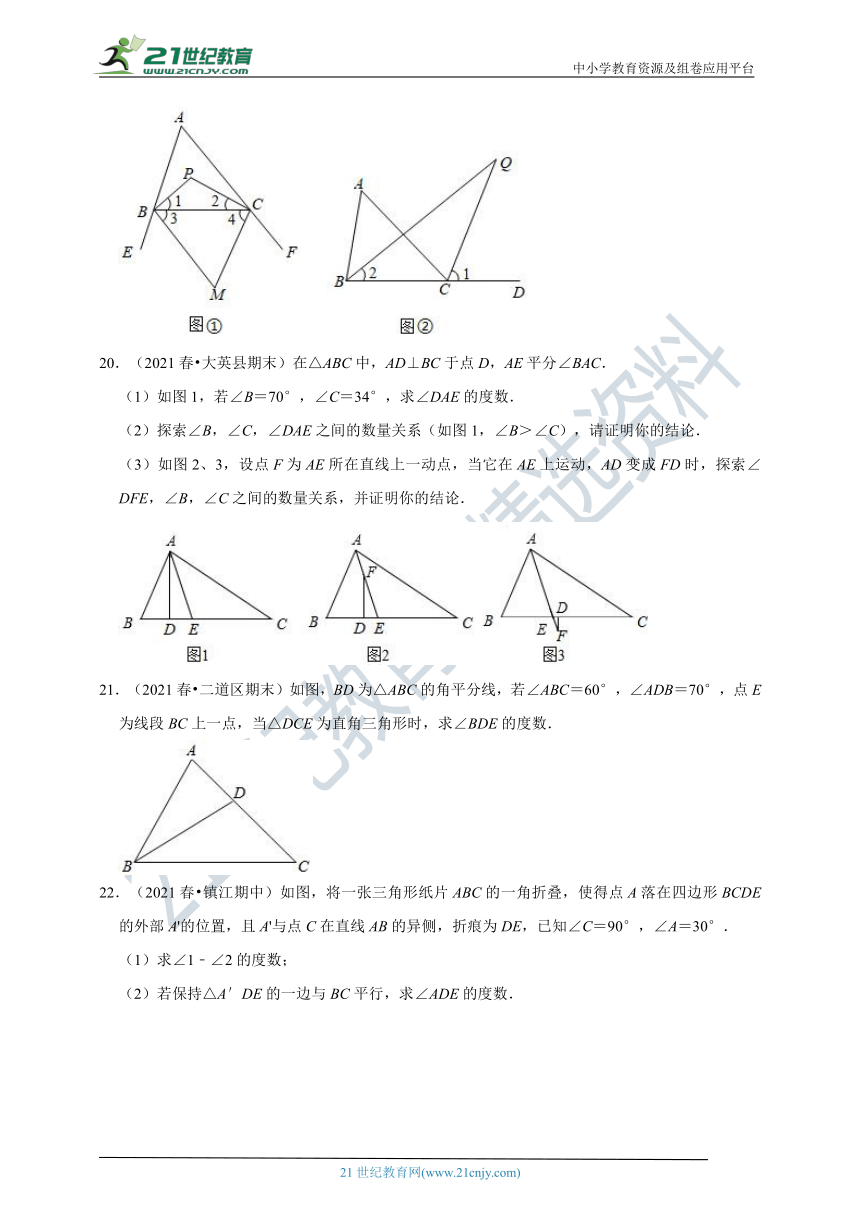
[问题呈现]如图①,点P是△ABC的内角平分线BP与CP的交点,点M是△ABC的外角平分线BM与CM的交点,则∠P=90°+∠A,∠M=90°﹣∠A.
说明∠P=90°+∠A如下:
∵BP、CP是△ABC的角平分线,
∴∠1=∠ABC,∠2=∠ABC.
∴∠A+2(∠1+∠2)=180°.…………①
∴∠1+∠2=90°﹣∠A.
∴∠P=180°﹣(∠1+∠2)=90°+∠A.
请你仔细阅读理解上面的说理过程,完成下列问题:
(1)上述说理过程中步骤①的依据是
.
(2)结合图①,写出说明∠M=90°﹣∠A的说理过程.
[拓展延伸]如图②,点Q是△ABC的内角平分线BQ与△ABC的外角(∠ACD)平分线CQ的交点.若∠A=50°,则∠Q的大小为
度.
20.(2021春?大英县期末)在△ABC中,AD⊥BC于点D,AE平分∠BAC.
(1)如图1,若∠B=70°,∠C=34°,求∠DAE的度数.
(2)探索∠B,∠C,∠DAE之间的数量关系(如图1,∠B>∠C),请证明你的结论.
(3)如图2、3,设点F为AE所在直线上一动点,当它在AE上运动,AD变成FD时,探索∠DFE,∠B,∠C之间的数量关系,并证明你的结论.
21.(2021春?二道区期末)如图,BD为△ABC的角平分线,若∠ABC=60°,∠ADB=70°,点E为线段BC上一点,当△DCE为直角三角形时,求∠BDE的度数.
22.(2021春?镇江期中)如图,将一张三角形纸片ABC的一角折叠,使得点A落在四边形BCDE的外部A'的位置,且A'与点C在直线AB的异侧,折痕为DE,已知∠C=90°,∠A=30°.
(1)求∠1﹣∠2的度数;
(2)若保持△A′DE的一边与BC平行,求∠ADE的度数.
答案与解析
一.选择题
1.(2021春?历下区期中)在下列条件:①∠A+∠B=∠C,②∠A:∠B:∠C=5:3:2,③∠A=90°﹣∠B,④∠A=2∠B=3∠C中,能确定△ABC是直角三角形的条件有( )
A.1个
B.2个
C.3个
D.4个
【解析】解:①∵∠A+∠B=∠C,
∴2∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形;
②∵∠A:∠B:∠C=5:3:2,
设∠A=5x,则∠B=3x,∠C=2x,
∴5x+2x+3x=180,
解得:x=18°,
∴∠5=18°×5=90°,
∴△ABC是直角三角形;
③∵∠A=90°﹣∠B,
∴∠A+∠B=90°,
∴∠C=180°﹣90°=90°,
∴△ABC是直角三角形;
④∵3∠C=2∠B=∠A,
∴∠A+∠B+∠C=∠A+∠A+∠A=180°,
∴∠A=()°,
∴△ABC为钝角三角形.
∴能确定△ABC是直角三角形的有①②③共3个,
故选:C.
2.(2021春?娄星区校级期中)已知在Rt△ABC中,∠B=90°,∠C=35°,则∠A等于( )
A.35°
B.45°
C.55°
D.65°
【解析】解:在Rt△ABC中,∠B=90°,∠C=35°,
则∠A=90°﹣35°=55°,
故选:C.
3.(2021?河池)如图,∠A=40°,∠CBD是△ABC的外角,∠CBD=120°,则∠C的大小是( )
A.90°
B.80°
C.60°
D.40°
【解析】解:由三角形的外角性质得,∠C=∠CBD﹣∠A=120°﹣40°=80°.
故选:B.
4.(2021?平谷区一模)如图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D,则下列结论不一定成立的是( )
A.∠1+∠2=90°
B.∠2=∠3
C.∠1=∠4
D.∠1=30°
【解析】解:A.∵∠ACB=90°,
∴∠1+∠2=90°,故本选项不符合题意;
B.∵CD⊥AB,
∴∠ADC=90°,
∴∠1+∠3=90°,
∵∠1+∠2=90°,
∴∠2=∠3,故本选项不符合题意;
C.∵CD⊥AB,
∴∠BDC=90°,
∴∠2+∠4=90°,
∵∠1+∠2=90°,
∴∠1=∠4,故本选项不符合题意;
D.根据已知条件不能推出∠1=30°,故本选项符合题意;
故选:D.
5.(2020秋?芜湖期中)如图,△ABC中,∠A=20°,沿BE将此三角形对折,又沿BA′再一次对折,点C落在BE上的C′处,此时∠C′DB=74°,则原三角形的∠C的度数为( )
A.27°
B.59°
C.69°
D.79°
【解析】解如图,∵△ABC沿BE将此三角形对折,又沿BA′再一次对折,点C落在BE上的C′处,
∴∠1=∠2,∠2=∠3,∠CDB=∠C′DB=74°,
∴∠1=∠2=∠3,
∴∠ABC=3∠3,
在△BCD中,∠3+∠C+∠CDB=180°,
∴∠3+∠C=180°﹣74°=106°,
在△ABC中,
∵∠A+∠ABC+∠C=180°,
∴20°+2∠3+(∠3+∠C)=180°,
即20°+2∠3+106°=180°,
∴∠3=27°,
∴∠ABC=3∠3=81°,
∠C=106°﹣27°=79°,
故选:D.
6.(2020春?石狮市期末)在直角三角形ABC中,∠A:∠B:∠C=2:m:4,则m的值是( )
A.3
B.4
C.2或6
D.2或4
【解析】解:设∠A、∠B、∠C的度数分别为2x、mx、4x,
当∠C为直角时,2x+mx=4x,
解得,m=2,
当∠B为直角时,2x+4x=mx,
解得,m=6,
故选:C.
7.(2021春?永年区期末)如图,BF是∠ABD的平分线,CE是∠ACD的平分线,BF与CE交于点G,若∠BDC=140°,∠BGC=110°,则∠A的度数为( )
A.50°
B.55°
C.70°
D.80°
【解析】解:连接BC.
∵∠BDC=140°,
∴∠DBC+∠DCB=180°﹣140°=40°,
∵∠BGC=110°,
∴∠GBC+∠GCB=180°﹣110°=70°,
∵BF是∠ABD的平分线,CE是∠ACD的平分线,
∴∠GBD+∠GCD=∠ABD+∠ACD=30°,
∴∠ABC+∠ACB=100°,
∴∠A=180°﹣100°=80°.
故选:D.
8.(2021春?建平县期末)定义:当三角形中一个内角α是另一个内角的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的一个内角为48°,那么这个“特征角”α的度数为( )
A.48°
B.96°
C.88°或48°
D.48°或96°或88°
【解析】解:设三角形的三个内角分别是∠1、∠2、α且α=2∠1.
当α=48°,则∠1=24°.
当∠1=48°,则α=2∠1=96°.
当∠2=48°,则∠1+α=180°﹣∠2=132°.
∴3∠1=132°.
∴∠1=44°.
∴α=2∠1=88°.
综上:“特征角”α可能为48°或96°或88°.
故选:D.
9.(2021春?闵行区校级月考)下列说法中错误的是( )
A.三角形的三个内角中,最多有一个钝角
B.三角形三个内角中,至少有两个锐角
C.直角三角形中有两个锐角互余
D.三角形中两个内角和必大于90°
【解析】解:A、三角形的三个内角中,最多有一个钝角,正确.
B、三角形三个内角中,至少有两个锐角,正确.
C、直角三角形中有两个锐角互余,正确,
D、三角形中两个内角和必大于90°,错误,比如钝角三角形的两个锐角的和小于90°.
故选:D.
10.(2021春?周村区月考)如图,在△CEF中,∠E=80°,∠F=55°,AB∥CF,AD∥CE,连接BC,CD,则∠A的度数是( )
A.45°
B.50°
C.55°
D.80°
【解析】解:连接AC并延长交EF于点G.
∵AB∥CF,
∴∠BAC=∠FCG,
∵AD∥CE,
∴∠DAC=∠ECG,
∴∠BAD=∠BAC+∠DAC=∠FCG+∠ECG=∠ECF,
在△CEF中,∠E=80°,∠F=55°,
∴∠ECF=180°﹣∠E﹣∠F=180°﹣80°﹣55°=45°,
∴∠BAD=∠ECF=45°.
故选:A.
二.填空题
11.(2021春?铁西区期中)在△ABC中,∠A:∠B:∠C=4:4:7,则∠C的度数为 84 °.
【解析】解:在△ABC中,∠A:∠B:∠C=4:4:7,
∴设∠A=4x,∠B=4x,∠C=7x,
∵∠A+∠B+∠C=180°,
∴4x+4x+7x=180°,
解得:x=12°,
∴∠C=7×12°=84°.
故答案为:84.
12.(2021春?乐清市期末)如图,直线a,b所成的角跑到画板外面了,某同学发现只要量出一条直线分别与直线a,b相交所形成的角的度数就可求得该角,已知∠1=71°,∠2=78°,则直线a,b所形成的角的度数为
31 °.
【解析】解:直线a,b∠交于点A,与边框的交点分别为B,C,如图,
∵∠1=71°,∠2=78°,
∴∠ABC=∠1=71°,∠ACB=∠2=78°,
∵∠A+∠ABC+∠ACB=180°,
∴∠A=180°﹣71°﹣78°=31°,
故答案为31.
13.(2020秋?前郭县期末)如图,C岛在A岛的北偏东45°方向,在B岛的北偏西25°方向,则∠ACB= 70 °.
【解析】解:连接AB.
∵C岛在A岛的北偏东45°方向,在B岛的北偏25°方向,
∴∠CAB+∠ABC=180°﹣(45°+25°)=110°,
∵三角形内角和是180°,
∴∠ACB=180°﹣(∠CAB+∠ABC)=180°﹣110°=70°.
故答案为:70.
14.(2021春?沙坪坝区校级期中)如图,在Rt△ABC中,∠B=90°,∠A=60°.将三角形沿EF翻折,使点C与边AB上的D点重合.若∠EFD=2∠AED,则∠AED的度数为 40° .
【解析】解:设∠EFD=2∠AED=2x.
由折叠性质可知,∠EDF=∠C=90°﹣∠A=90°﹣60°=30°,
∠DEF=∠CEF,
∴∠DEF=180°﹣∠EDF﹣∠EFD=180°﹣30°﹣2x=150°﹣2x,
∴∠CEF=150°﹣2x,
∵∠DEF+∠CEF+∠AED=180°,
∴150°﹣2x+150°﹣2x+x=180°,
解得x=40°,
即∠AED=40°.
故答案为:40°.
15.(2021春?泌阳县期末)在三角形的所有外角(每个顶点处只取一个外角)中,锐角最多有
1 个.
【解析】解:∵三角形的内角最多有1个钝角,
∴三角形的三个外角中,锐角最多有1个.
故答案为:1.
16.(2021春?江汉区期末)在△ABC中,∠BAC=50°,BE、CF是△ABC的高,直线BE、CF交于点H,则∠BHC的度数是
50°或130° .
【解析】解:
如图1点H在△ABC的内部,
∵BE,CF是△ABC的高,
∴∠BEA=∠CFA=90°,
∴∠EHF=180°﹣∠A=180°﹣50°=130°,
∴∠BHC=130°;
如图2,点H在△ABC的外部,
同理得到∠BEA=∠CFA=90°,
∵∠HCE=∠ACF,
∴∠BHC=∠A=50°,
综上所述,∠BHC的度数为50°或130°.
故答案为:50°或130°.
三.解答题
17.(2021春?望城区期末)如图,在△ABC
中,∠B=40°,∠C=110°.
(1)画出下列图形:
①BC边上的高AD;
②∠A的角平分线AE.
(2)试求∠DAE的度数.
【解析】(1)如图所示;
(2)在△ABC中,∠BAC=180°﹣∠B﹣∠ACB=180°﹣40°﹣110°=30°,
∵AE平分∠BAC,
∴∠BAE=∠BAC=15°,
在Rt△ADB中,∠BAD=90°﹣∠B=50°,
∴∠DAE=∠DAB﹣∠BAE=35°.
18.(2021春?淮阳区校级期末)如图,已知CD是△ABC中∠ACB的外角平分线.
(1)若∠ACE=150°,∠BAC=100°,求∠B的大小;
(2)请说明∠BAC>∠B.
【解析】解:(1)∵∠ACE=150°,∠BAC=100°,
∴∠B=∠ACE﹣∠BAC=150°﹣100°=50°;
(2)∵CD是△ABC中∠ACB的外角平分线,
∴∠ACD=∠ECD,
∵∠BAC是△ACD的外角,
∴∠BAC>∠ACD,
∴∠BAC>∠ECD,
∵∠ECD是△BCD的外角,
∴∠ECD>∠B,
∴∠BAC>∠B.
19.(2021春?长春期末)[规律探索]探索三角形的内(外)角平分线形成的角的规律:
在三角形中,由三角形的内角平分线外角平分线所形成的角存在一定的规律.
规律1:三角形的两个内角的平分线形成的钝角等于90°加上第三个内角度数的一半;
规律2:三角形的两个外角的平分线形成的锐角等于90°减去与这两个外角不相邻的内角度数的一半.
[问题呈现]如图①,点P是△ABC的内角平分线BP与CP的交点,点M是△ABC的外角平分线BM与CM的交点,则∠P=90°+∠A,∠M=90°﹣∠A.
说明∠P=90°+∠A如下:
∵BP、CP是△ABC的角平分线,
∴∠1=∠ABC,∠2=∠ABC.
∴∠A+2(∠1+∠2)=180°.…………①
∴∠1+∠2=90°﹣∠A.
∴∠P=180°﹣(∠1+∠2)=90°+∠A.
请你仔细阅读理解上面的说理过程,完成下列问题:
(1)上述说理过程中步骤①的依据是
三角形内角和等于180° .
(2)结合图①,写出说明∠M=90°﹣∠A的说理过程.
[拓展延伸]如图②,点Q是△ABC的内角平分线BQ与△ABC的外角(∠ACD)平分线CQ的交点.若∠A=50°,则∠Q的大小为
25 度.
【解析】解:【问题呈现】
(1)证明过程中步骤(2)的依据是三角形内角和等于180°,
故答案为:三角形内角和等于180°;
(2)∵BM、CM是△ABC的外角平分线,
∴∠3=∠EBC,∠4=∠FCB,
∴∠ABC=180°﹣2∠3,∠ACB=180°﹣2∠4,
∴∠A+(180°﹣2∠3)+(180°﹣2∠4)=180°,
∴∠3+∠4=90°+∠A,
∵∠3+∠4+∠M=180°,
∴∠M=180°﹣(90°+∠A)=90°﹣∠A;
【拓展延伸】
∵CQ平分∠ACD,
∴∠1=∠ACD,
∵BQ平分∠ABC,
∴∠2=∠ABC,
∵∠ACD=∠A+∠ABC,
∴∠A=∠ACD﹣∠ABC=2(∠1﹣∠2),
∵∠1=∠2+∠Q,
∴∠Q=∠1=∠2,
∴∠A=2∠Q,
即∠Q=∠A=25,
故答案为:25.
20.(2021春?大英县期末)在△ABC中,AD⊥BC于点D,AE平分∠BAC.
(1)如图1,若∠B=70°,∠C=34°,求∠DAE的度数.
(2)探索∠B,∠C,∠DAE之间的数量关系(如图1,∠B>∠C),请证明你的结论.
(3)如图2、3,设点F为AE所在直线上一动点,当它在AE上运动,AD变成FD时,探索∠DFE,∠B,∠C之间的数量关系,并证明你的结论.
【解析】解:(1)在△ABC中,∠B=70°,∠C=34°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣70°﹣34°=76°,
∵AE平分∠BAC,
∴∠EAC=∠BAC=×76°=38°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠DAC=90°﹣∠C=90°﹣34°=56°,
∴∠DAE=∠DAC﹣∠EAC=56°﹣38°=18°;
(2)如图1,∠B,∠C,∠DAE的关系为:∠DAE=(∠B﹣∠C),
证明∵∠BAC=180°﹣∠B﹣∠C,AE平分∠BAC,
∴∠CAE=∠BAC=(180°﹣∠B﹣∠C)=90°﹣∠B﹣∠C,
∵AD⊥BC,
∴∠ADC=90°,
∴∠CAD=90°﹣∠C,
∴∠DAE=∠DAC﹣∠EAC=90°﹣∠C﹣(90°﹣∠B﹣∠C)=(∠B﹣∠C);
(3)∠DFE,∠B,∠C之间的数量关系为:∠DFE=(∠B﹣∠C),
证明:分两种情况:①如图2,当点F在AE上时,作AH⊥BC于H,
由(2)得:∠HAE=(∠B﹣∠C),
∵AH⊥BC,FD⊥BC,
∵AH∥FD,
∴∠DFE=∠HAE,
∴∠DFE=(∠B﹣∠C),
②如图3,当点F在AE上时,作AH⊥BC于H,
由(2)得:∠HAE=(∠B﹣∠C),
∵AH⊥BC,FD⊥BC,
∵AH∥FD,
∴∠DFE=∠HAE,
∴∠DFE=(∠B﹣∠C),
综上所述,∠DFE,∠B,∠C之间的数量关系为:∠DFE=(∠B﹣∠C).
21.(2021春?二道区期末)如图,BD为△ABC的角平分线,若∠ABC=60°,∠ADB=70°,点E为线段BC上一点,当△DCE为直角三角形时,求∠BDE的度数.
【解析】解:(1)∵BD为△ABC的角平分线,∠ABC=60°
∴∠DBC=30°,
又∵∠ADB是△BDC的外角,∠ADB=70°,
∴∠ADB=∠DBC+∠C,
∴∠C=∠ADB﹣∠DBC=40°,∠BDC=180°﹣70°=110°,
当∠EDC=90°时,如图1,
则∠CDE=90°,
∠BDE=110°﹣90°=20°;
情况二:如图2,当∠CED=90°时,
∠EDC=90°﹣∠C=90°﹣40°=50°,
∠BDE=110°=50°=60°,
综上所述,∠BDE的度数为20°或60°.
22.(2021春?镇江期中)如图,将一张三角形纸片ABC的一角折叠,使得点A落在四边形BCDE的外部A'的位置,且A'与点C在直线AB的异侧,折痕为DE,已知∠C=90°,∠A=30°.
(1)求∠1﹣∠2的度数;
(2)若保持△A′DE的一边与BC平行,求∠ADE的度数.
【解析】解:(1)由折叠可知,∠A′=∠A=30°,
在△A′EF中,∠A′+∠2+∠A′FE=180°,
∴∠2=180°﹣∠A′﹣∠A′FE=150°﹣∠A′FE,
在△ABC中,∠B=180°﹣∠C﹣∠A=60°,
在四边形BCDF中,∠1+∠C+∠B+∠BFD=360°,
∴∠1=360°﹣∠C﹣∠B﹣∠BFD=210°﹣∠BFD,
∵∠BFD=∠A′FE,
∴∠1﹣∠2=210°﹣150°=60°;
(2)当DA'∥BC时,如图,∠A′DA=∠ACB=90°,
∵△ADE沿DE折叠到△A′DE,
∴∠ADE=∠A′DE=∠ADA′=45°,
当EA'∥BC时,如图,∠2=∠ABC=60°.
由(1)知,∠1﹣∠2=60°,
∴∠1=∠2+60°=120°,
∵△ADE沿DE折叠到△A′DE,
∴∠ADE=∠A′DE=∠ADA′=(180°﹣∠1)=30°.
综上所述∠ADE的度数为:45°或30°.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
人教版八年级上
11.2与三角形有关的角同步练习
一.选择题
1.(2021春?历下区期中)在下列条件:①∠A+∠B=∠C,②∠A:∠B:∠C=5:3:2,③∠A=90°﹣∠B,④∠A=2∠B=3∠C中,能确定△ABC是直角三角形的条件有( )
A.1个
B.2个
C.3个
D.4个
2.(2021春?娄星区校级期中)已知在Rt△ABC中,∠B=90°,∠C=35°,则∠A等于( )
A.35°
B.45°
C.55°
D.65°
3.(2021?河池)如图,∠A=40°,∠CBD是△ABC的外角,∠CBD=120°,则∠C的大小是( )
A.90°
B.80°
C.60°
D.40°
4.(2021?平谷区一模)如图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D,则下列结论不一定成立的是( )
A.∠1+∠2=90°
B.∠2=∠3
C.∠1=∠4
D.∠1=30°
5.(2020秋?芜湖期中)如图,△ABC中,∠A=20°,沿BE将此三角形对折,又沿BA′再一次对折,点C落在BE上的C′处,此时∠C′DB=74°,则原三角形的∠C的度数为( )
A.27°
B.59°
C.69°
D.79°
6.(2020春?石狮市期末)在直角三角形ABC中,∠A:∠B:∠C=2:m:4,则m的值是( )
A.3
B.4
C.2或6
D.2或4
7.(2021春?永年区期末)如图,BF是∠ABD的平分线,CE是∠ACD的平分线,BF与CE交于点G,若∠BDC=140°,∠BGC=110°,则∠A的度数为( )
A.50°
B.55°
C.70°
D.80°
8.(2021春?建平县期末)定义:当三角形中一个内角α是另一个内角的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的一个内角为48°,那么这个“特征角”α的度数为( )
A.48°
B.96°
C.88°或48°
D.48°或96°或88°
9.(2021春?闵行区校级月考)下列说法中错误的是( )
A.三角形的三个内角中,最多有一个钝角
B.三角形三个内角中,至少有两个锐角
C.直角三角形中有两个锐角互余
D.三角形中两个内角和必大于90°
10.(2021春?周村区月考)如图,在△CEF中,∠E=80°,∠F=55°,AB∥CF,AD∥CE,连接BC,CD,则∠A的度数是( )
A.45°
B.50°
C.55°
D.80°
二.填空题
11.(2021春?铁西区期中)在△ABC中,∠A:∠B:∠C=4:4:7,则∠C的度数为
°.
12.(2021春?乐清市期末)如图,直线a,b所成的角跑到画板外面了,某同学发现只要量出一条直线分别与直线a,b相交所形成的角的度数就可求得该角,已知∠1=71°,∠2=78°,则直线a,b所形成的角的度数为
°.
13.(2020秋?前郭县期末)如图,C岛在A岛的北偏东45°方向,在B岛的北偏西25°方向,则∠ACB=
°.
14.(2021春?沙坪坝区校级期中)如图,在Rt△ABC中,∠B=90°,∠A=60°.将三角形沿EF翻折,使点C与边AB上的D点重合.若∠EFD=2∠AED,则∠AED的度数为
.
15.(2021春?泌阳县期末)在三角形的所有外角(每个顶点处只取一个外角)中,锐角最多有
个.
16.(2021春?江汉区期末)在△ABC中,∠BAC=50°,BE、CF是△ABC的高,直线BE、CF交于点H,则∠BHC的度数是
.
三.解答题
17.(2021春?望城区期末)如图,在△ABC
中,∠B=40°,∠C=110°.
(1)画出下列图形:
①BC边上的高AD;
②∠A的角平分线AE.
(2)试求∠DAE的度数.
18.(2021春?淮阳区校级期末)如图,已知CD是△ABC中∠ACB的外角平分线.
(1)若∠ACE=150°,∠BAC=100°,求∠B的大小;
(2)请说明∠BAC>∠B.
19.(2021春?长春期末)[规律探索]探索三角形的内(外)角平分线形成的角的规律:
在三角形中,由三角形的内角平分线外角平分线所形成的角存在一定的规律.
规律1:三角形的两个内角的平分线形成的钝角等于90°加上第三个内角度数的一半;
规律2:三角形的两个外角的平分线形成的锐角等于90°减去与这两个外角不相邻的内角度数的一半.
[问题呈现]如图①,点P是△ABC的内角平分线BP与CP的交点,点M是△ABC的外角平分线BM与CM的交点,则∠P=90°+∠A,∠M=90°﹣∠A.
说明∠P=90°+∠A如下:
∵BP、CP是△ABC的角平分线,
∴∠1=∠ABC,∠2=∠ABC.
∴∠A+2(∠1+∠2)=180°.…………①
∴∠1+∠2=90°﹣∠A.
∴∠P=180°﹣(∠1+∠2)=90°+∠A.
请你仔细阅读理解上面的说理过程,完成下列问题:
(1)上述说理过程中步骤①的依据是
.
(2)结合图①,写出说明∠M=90°﹣∠A的说理过程.
[拓展延伸]如图②,点Q是△ABC的内角平分线BQ与△ABC的外角(∠ACD)平分线CQ的交点.若∠A=50°,则∠Q的大小为
度.
20.(2021春?大英县期末)在△ABC中,AD⊥BC于点D,AE平分∠BAC.
(1)如图1,若∠B=70°,∠C=34°,求∠DAE的度数.
(2)探索∠B,∠C,∠DAE之间的数量关系(如图1,∠B>∠C),请证明你的结论.
(3)如图2、3,设点F为AE所在直线上一动点,当它在AE上运动,AD变成FD时,探索∠DFE,∠B,∠C之间的数量关系,并证明你的结论.
21.(2021春?二道区期末)如图,BD为△ABC的角平分线,若∠ABC=60°,∠ADB=70°,点E为线段BC上一点,当△DCE为直角三角形时,求∠BDE的度数.
22.(2021春?镇江期中)如图,将一张三角形纸片ABC的一角折叠,使得点A落在四边形BCDE的外部A'的位置,且A'与点C在直线AB的异侧,折痕为DE,已知∠C=90°,∠A=30°.
(1)求∠1﹣∠2的度数;
(2)若保持△A′DE的一边与BC平行,求∠ADE的度数.
答案与解析
一.选择题
1.(2021春?历下区期中)在下列条件:①∠A+∠B=∠C,②∠A:∠B:∠C=5:3:2,③∠A=90°﹣∠B,④∠A=2∠B=3∠C中,能确定△ABC是直角三角形的条件有( )
A.1个
B.2个
C.3个
D.4个
【解析】解:①∵∠A+∠B=∠C,
∴2∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形;
②∵∠A:∠B:∠C=5:3:2,
设∠A=5x,则∠B=3x,∠C=2x,
∴5x+2x+3x=180,
解得:x=18°,
∴∠5=18°×5=90°,
∴△ABC是直角三角形;
③∵∠A=90°﹣∠B,
∴∠A+∠B=90°,
∴∠C=180°﹣90°=90°,
∴△ABC是直角三角形;
④∵3∠C=2∠B=∠A,
∴∠A+∠B+∠C=∠A+∠A+∠A=180°,
∴∠A=()°,
∴△ABC为钝角三角形.
∴能确定△ABC是直角三角形的有①②③共3个,
故选:C.
2.(2021春?娄星区校级期中)已知在Rt△ABC中,∠B=90°,∠C=35°,则∠A等于( )
A.35°
B.45°
C.55°
D.65°
【解析】解:在Rt△ABC中,∠B=90°,∠C=35°,
则∠A=90°﹣35°=55°,
故选:C.
3.(2021?河池)如图,∠A=40°,∠CBD是△ABC的外角,∠CBD=120°,则∠C的大小是( )
A.90°
B.80°
C.60°
D.40°
【解析】解:由三角形的外角性质得,∠C=∠CBD﹣∠A=120°﹣40°=80°.
故选:B.
4.(2021?平谷区一模)如图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D,则下列结论不一定成立的是( )
A.∠1+∠2=90°
B.∠2=∠3
C.∠1=∠4
D.∠1=30°
【解析】解:A.∵∠ACB=90°,
∴∠1+∠2=90°,故本选项不符合题意;
B.∵CD⊥AB,
∴∠ADC=90°,
∴∠1+∠3=90°,
∵∠1+∠2=90°,
∴∠2=∠3,故本选项不符合题意;
C.∵CD⊥AB,
∴∠BDC=90°,
∴∠2+∠4=90°,
∵∠1+∠2=90°,
∴∠1=∠4,故本选项不符合题意;
D.根据已知条件不能推出∠1=30°,故本选项符合题意;
故选:D.
5.(2020秋?芜湖期中)如图,△ABC中,∠A=20°,沿BE将此三角形对折,又沿BA′再一次对折,点C落在BE上的C′处,此时∠C′DB=74°,则原三角形的∠C的度数为( )
A.27°
B.59°
C.69°
D.79°
【解析】解如图,∵△ABC沿BE将此三角形对折,又沿BA′再一次对折,点C落在BE上的C′处,
∴∠1=∠2,∠2=∠3,∠CDB=∠C′DB=74°,
∴∠1=∠2=∠3,
∴∠ABC=3∠3,
在△BCD中,∠3+∠C+∠CDB=180°,
∴∠3+∠C=180°﹣74°=106°,
在△ABC中,
∵∠A+∠ABC+∠C=180°,
∴20°+2∠3+(∠3+∠C)=180°,
即20°+2∠3+106°=180°,
∴∠3=27°,
∴∠ABC=3∠3=81°,
∠C=106°﹣27°=79°,
故选:D.
6.(2020春?石狮市期末)在直角三角形ABC中,∠A:∠B:∠C=2:m:4,则m的值是( )
A.3
B.4
C.2或6
D.2或4
【解析】解:设∠A、∠B、∠C的度数分别为2x、mx、4x,
当∠C为直角时,2x+mx=4x,
解得,m=2,
当∠B为直角时,2x+4x=mx,
解得,m=6,
故选:C.
7.(2021春?永年区期末)如图,BF是∠ABD的平分线,CE是∠ACD的平分线,BF与CE交于点G,若∠BDC=140°,∠BGC=110°,则∠A的度数为( )
A.50°
B.55°
C.70°
D.80°
【解析】解:连接BC.
∵∠BDC=140°,
∴∠DBC+∠DCB=180°﹣140°=40°,
∵∠BGC=110°,
∴∠GBC+∠GCB=180°﹣110°=70°,
∵BF是∠ABD的平分线,CE是∠ACD的平分线,
∴∠GBD+∠GCD=∠ABD+∠ACD=30°,
∴∠ABC+∠ACB=100°,
∴∠A=180°﹣100°=80°.
故选:D.
8.(2021春?建平县期末)定义:当三角形中一个内角α是另一个内角的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的一个内角为48°,那么这个“特征角”α的度数为( )
A.48°
B.96°
C.88°或48°
D.48°或96°或88°
【解析】解:设三角形的三个内角分别是∠1、∠2、α且α=2∠1.
当α=48°,则∠1=24°.
当∠1=48°,则α=2∠1=96°.
当∠2=48°,则∠1+α=180°﹣∠2=132°.
∴3∠1=132°.
∴∠1=44°.
∴α=2∠1=88°.
综上:“特征角”α可能为48°或96°或88°.
故选:D.
9.(2021春?闵行区校级月考)下列说法中错误的是( )
A.三角形的三个内角中,最多有一个钝角
B.三角形三个内角中,至少有两个锐角
C.直角三角形中有两个锐角互余
D.三角形中两个内角和必大于90°
【解析】解:A、三角形的三个内角中,最多有一个钝角,正确.
B、三角形三个内角中,至少有两个锐角,正确.
C、直角三角形中有两个锐角互余,正确,
D、三角形中两个内角和必大于90°,错误,比如钝角三角形的两个锐角的和小于90°.
故选:D.
10.(2021春?周村区月考)如图,在△CEF中,∠E=80°,∠F=55°,AB∥CF,AD∥CE,连接BC,CD,则∠A的度数是( )
A.45°
B.50°
C.55°
D.80°
【解析】解:连接AC并延长交EF于点G.
∵AB∥CF,
∴∠BAC=∠FCG,
∵AD∥CE,
∴∠DAC=∠ECG,
∴∠BAD=∠BAC+∠DAC=∠FCG+∠ECG=∠ECF,
在△CEF中,∠E=80°,∠F=55°,
∴∠ECF=180°﹣∠E﹣∠F=180°﹣80°﹣55°=45°,
∴∠BAD=∠ECF=45°.
故选:A.
二.填空题
11.(2021春?铁西区期中)在△ABC中,∠A:∠B:∠C=4:4:7,则∠C的度数为 84 °.
【解析】解:在△ABC中,∠A:∠B:∠C=4:4:7,
∴设∠A=4x,∠B=4x,∠C=7x,
∵∠A+∠B+∠C=180°,
∴4x+4x+7x=180°,
解得:x=12°,
∴∠C=7×12°=84°.
故答案为:84.
12.(2021春?乐清市期末)如图,直线a,b所成的角跑到画板外面了,某同学发现只要量出一条直线分别与直线a,b相交所形成的角的度数就可求得该角,已知∠1=71°,∠2=78°,则直线a,b所形成的角的度数为
31 °.
【解析】解:直线a,b∠交于点A,与边框的交点分别为B,C,如图,
∵∠1=71°,∠2=78°,
∴∠ABC=∠1=71°,∠ACB=∠2=78°,
∵∠A+∠ABC+∠ACB=180°,
∴∠A=180°﹣71°﹣78°=31°,
故答案为31.
13.(2020秋?前郭县期末)如图,C岛在A岛的北偏东45°方向,在B岛的北偏西25°方向,则∠ACB= 70 °.
【解析】解:连接AB.
∵C岛在A岛的北偏东45°方向,在B岛的北偏25°方向,
∴∠CAB+∠ABC=180°﹣(45°+25°)=110°,
∵三角形内角和是180°,
∴∠ACB=180°﹣(∠CAB+∠ABC)=180°﹣110°=70°.
故答案为:70.
14.(2021春?沙坪坝区校级期中)如图,在Rt△ABC中,∠B=90°,∠A=60°.将三角形沿EF翻折,使点C与边AB上的D点重合.若∠EFD=2∠AED,则∠AED的度数为 40° .
【解析】解:设∠EFD=2∠AED=2x.
由折叠性质可知,∠EDF=∠C=90°﹣∠A=90°﹣60°=30°,
∠DEF=∠CEF,
∴∠DEF=180°﹣∠EDF﹣∠EFD=180°﹣30°﹣2x=150°﹣2x,
∴∠CEF=150°﹣2x,
∵∠DEF+∠CEF+∠AED=180°,
∴150°﹣2x+150°﹣2x+x=180°,
解得x=40°,
即∠AED=40°.
故答案为:40°.
15.(2021春?泌阳县期末)在三角形的所有外角(每个顶点处只取一个外角)中,锐角最多有
1 个.
【解析】解:∵三角形的内角最多有1个钝角,
∴三角形的三个外角中,锐角最多有1个.
故答案为:1.
16.(2021春?江汉区期末)在△ABC中,∠BAC=50°,BE、CF是△ABC的高,直线BE、CF交于点H,则∠BHC的度数是
50°或130° .
【解析】解:
如图1点H在△ABC的内部,
∵BE,CF是△ABC的高,
∴∠BEA=∠CFA=90°,
∴∠EHF=180°﹣∠A=180°﹣50°=130°,
∴∠BHC=130°;
如图2,点H在△ABC的外部,
同理得到∠BEA=∠CFA=90°,
∵∠HCE=∠ACF,
∴∠BHC=∠A=50°,
综上所述,∠BHC的度数为50°或130°.
故答案为:50°或130°.
三.解答题
17.(2021春?望城区期末)如图,在△ABC
中,∠B=40°,∠C=110°.
(1)画出下列图形:
①BC边上的高AD;
②∠A的角平分线AE.
(2)试求∠DAE的度数.
【解析】(1)如图所示;
(2)在△ABC中,∠BAC=180°﹣∠B﹣∠ACB=180°﹣40°﹣110°=30°,
∵AE平分∠BAC,
∴∠BAE=∠BAC=15°,
在Rt△ADB中,∠BAD=90°﹣∠B=50°,
∴∠DAE=∠DAB﹣∠BAE=35°.
18.(2021春?淮阳区校级期末)如图,已知CD是△ABC中∠ACB的外角平分线.
(1)若∠ACE=150°,∠BAC=100°,求∠B的大小;
(2)请说明∠BAC>∠B.
【解析】解:(1)∵∠ACE=150°,∠BAC=100°,
∴∠B=∠ACE﹣∠BAC=150°﹣100°=50°;
(2)∵CD是△ABC中∠ACB的外角平分线,
∴∠ACD=∠ECD,
∵∠BAC是△ACD的外角,
∴∠BAC>∠ACD,
∴∠BAC>∠ECD,
∵∠ECD是△BCD的外角,
∴∠ECD>∠B,
∴∠BAC>∠B.
19.(2021春?长春期末)[规律探索]探索三角形的内(外)角平分线形成的角的规律:
在三角形中,由三角形的内角平分线外角平分线所形成的角存在一定的规律.
规律1:三角形的两个内角的平分线形成的钝角等于90°加上第三个内角度数的一半;
规律2:三角形的两个外角的平分线形成的锐角等于90°减去与这两个外角不相邻的内角度数的一半.
[问题呈现]如图①,点P是△ABC的内角平分线BP与CP的交点,点M是△ABC的外角平分线BM与CM的交点,则∠P=90°+∠A,∠M=90°﹣∠A.
说明∠P=90°+∠A如下:
∵BP、CP是△ABC的角平分线,
∴∠1=∠ABC,∠2=∠ABC.
∴∠A+2(∠1+∠2)=180°.…………①
∴∠1+∠2=90°﹣∠A.
∴∠P=180°﹣(∠1+∠2)=90°+∠A.
请你仔细阅读理解上面的说理过程,完成下列问题:
(1)上述说理过程中步骤①的依据是
三角形内角和等于180° .
(2)结合图①,写出说明∠M=90°﹣∠A的说理过程.
[拓展延伸]如图②,点Q是△ABC的内角平分线BQ与△ABC的外角(∠ACD)平分线CQ的交点.若∠A=50°,则∠Q的大小为
25 度.
【解析】解:【问题呈现】
(1)证明过程中步骤(2)的依据是三角形内角和等于180°,
故答案为:三角形内角和等于180°;
(2)∵BM、CM是△ABC的外角平分线,
∴∠3=∠EBC,∠4=∠FCB,
∴∠ABC=180°﹣2∠3,∠ACB=180°﹣2∠4,
∴∠A+(180°﹣2∠3)+(180°﹣2∠4)=180°,
∴∠3+∠4=90°+∠A,
∵∠3+∠4+∠M=180°,
∴∠M=180°﹣(90°+∠A)=90°﹣∠A;
【拓展延伸】
∵CQ平分∠ACD,
∴∠1=∠ACD,
∵BQ平分∠ABC,
∴∠2=∠ABC,
∵∠ACD=∠A+∠ABC,
∴∠A=∠ACD﹣∠ABC=2(∠1﹣∠2),
∵∠1=∠2+∠Q,
∴∠Q=∠1=∠2,
∴∠A=2∠Q,
即∠Q=∠A=25,
故答案为:25.
20.(2021春?大英县期末)在△ABC中,AD⊥BC于点D,AE平分∠BAC.
(1)如图1,若∠B=70°,∠C=34°,求∠DAE的度数.
(2)探索∠B,∠C,∠DAE之间的数量关系(如图1,∠B>∠C),请证明你的结论.
(3)如图2、3,设点F为AE所在直线上一动点,当它在AE上运动,AD变成FD时,探索∠DFE,∠B,∠C之间的数量关系,并证明你的结论.
【解析】解:(1)在△ABC中,∠B=70°,∠C=34°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣70°﹣34°=76°,
∵AE平分∠BAC,
∴∠EAC=∠BAC=×76°=38°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠DAC=90°﹣∠C=90°﹣34°=56°,
∴∠DAE=∠DAC﹣∠EAC=56°﹣38°=18°;
(2)如图1,∠B,∠C,∠DAE的关系为:∠DAE=(∠B﹣∠C),
证明∵∠BAC=180°﹣∠B﹣∠C,AE平分∠BAC,
∴∠CAE=∠BAC=(180°﹣∠B﹣∠C)=90°﹣∠B﹣∠C,
∵AD⊥BC,
∴∠ADC=90°,
∴∠CAD=90°﹣∠C,
∴∠DAE=∠DAC﹣∠EAC=90°﹣∠C﹣(90°﹣∠B﹣∠C)=(∠B﹣∠C);
(3)∠DFE,∠B,∠C之间的数量关系为:∠DFE=(∠B﹣∠C),
证明:分两种情况:①如图2,当点F在AE上时,作AH⊥BC于H,
由(2)得:∠HAE=(∠B﹣∠C),
∵AH⊥BC,FD⊥BC,
∵AH∥FD,
∴∠DFE=∠HAE,
∴∠DFE=(∠B﹣∠C),
②如图3,当点F在AE上时,作AH⊥BC于H,
由(2)得:∠HAE=(∠B﹣∠C),
∵AH⊥BC,FD⊥BC,
∵AH∥FD,
∴∠DFE=∠HAE,
∴∠DFE=(∠B﹣∠C),
综上所述,∠DFE,∠B,∠C之间的数量关系为:∠DFE=(∠B﹣∠C).
21.(2021春?二道区期末)如图,BD为△ABC的角平分线,若∠ABC=60°,∠ADB=70°,点E为线段BC上一点,当△DCE为直角三角形时,求∠BDE的度数.
【解析】解:(1)∵BD为△ABC的角平分线,∠ABC=60°
∴∠DBC=30°,
又∵∠ADB是△BDC的外角,∠ADB=70°,
∴∠ADB=∠DBC+∠C,
∴∠C=∠ADB﹣∠DBC=40°,∠BDC=180°﹣70°=110°,
当∠EDC=90°时,如图1,
则∠CDE=90°,
∠BDE=110°﹣90°=20°;
情况二:如图2,当∠CED=90°时,
∠EDC=90°﹣∠C=90°﹣40°=50°,
∠BDE=110°=50°=60°,
综上所述,∠BDE的度数为20°或60°.
22.(2021春?镇江期中)如图,将一张三角形纸片ABC的一角折叠,使得点A落在四边形BCDE的外部A'的位置,且A'与点C在直线AB的异侧,折痕为DE,已知∠C=90°,∠A=30°.
(1)求∠1﹣∠2的度数;
(2)若保持△A′DE的一边与BC平行,求∠ADE的度数.
【解析】解:(1)由折叠可知,∠A′=∠A=30°,
在△A′EF中,∠A′+∠2+∠A′FE=180°,
∴∠2=180°﹣∠A′﹣∠A′FE=150°﹣∠A′FE,
在△ABC中,∠B=180°﹣∠C﹣∠A=60°,
在四边形BCDF中,∠1+∠C+∠B+∠BFD=360°,
∴∠1=360°﹣∠C﹣∠B﹣∠BFD=210°﹣∠BFD,
∵∠BFD=∠A′FE,
∴∠1﹣∠2=210°﹣150°=60°;
(2)当DA'∥BC时,如图,∠A′DA=∠ACB=90°,
∵△ADE沿DE折叠到△A′DE,
∴∠ADE=∠A′DE=∠ADA′=45°,
当EA'∥BC时,如图,∠2=∠ABC=60°.
由(1)知,∠1﹣∠2=60°,
∴∠1=∠2+60°=120°,
∵△ADE沿DE折叠到△A′DE,
∴∠ADE=∠A′DE=∠ADA′=(180°﹣∠1)=30°.
综上所述∠ADE的度数为:45°或30°.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
