11.3 多边形及其内角和同步练习(含解析)
文档属性
| 名称 | 11.3 多边形及其内角和同步练习(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 977.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-03 21:28:17 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版八年级上
11.3多边形及其内角和同步练习
一.选择题
1.(2021春?夏津县期末)如果一个多边形的每一个外角都是30°,那么这个多边形的边数是( )
A.12
B.13
C.14
D.15
2.(2021春?凤翔县期末)正多边形的一个内角是120°,则这个正多边形的边数为( )
A.4
B.8
C.6
D.12
3.(2021春?长春期末)如图,将四边形ABCD去掉一个80°的角得到一个五边形BCDEF,则∠1与∠2的和为( )
A.240°
B.260°
C.280°
D.300°
4.(2021春?洪洞县期末)如果一个正多边形的内角和是外角和的4倍,那么这个正多边形的边数为( )
A.7
B.8
C.9
D.10
5.(2021春?偃师市期末)多边形的边数由3增加到2021时,其外角和的度数( )
A.不能确定
B.减少
C.增加
D.不变
6.(2021春?宛城区期末)小聪为某机器人编制一段程序,如果机器人以0.5m/s的速度在平地上按照图中的步骤行走,那么该机器人从开始到停止所需的时间为( )
A.12s
B.24s
C.48s
D.60s
7.(2021春?渠县校级期末)已知在一个凸多边形中,和一个内角相邻的外角与其余内角度数总和为600°,则这个多边形的边数是( )
A.5
B.6
C.7
D.5或6
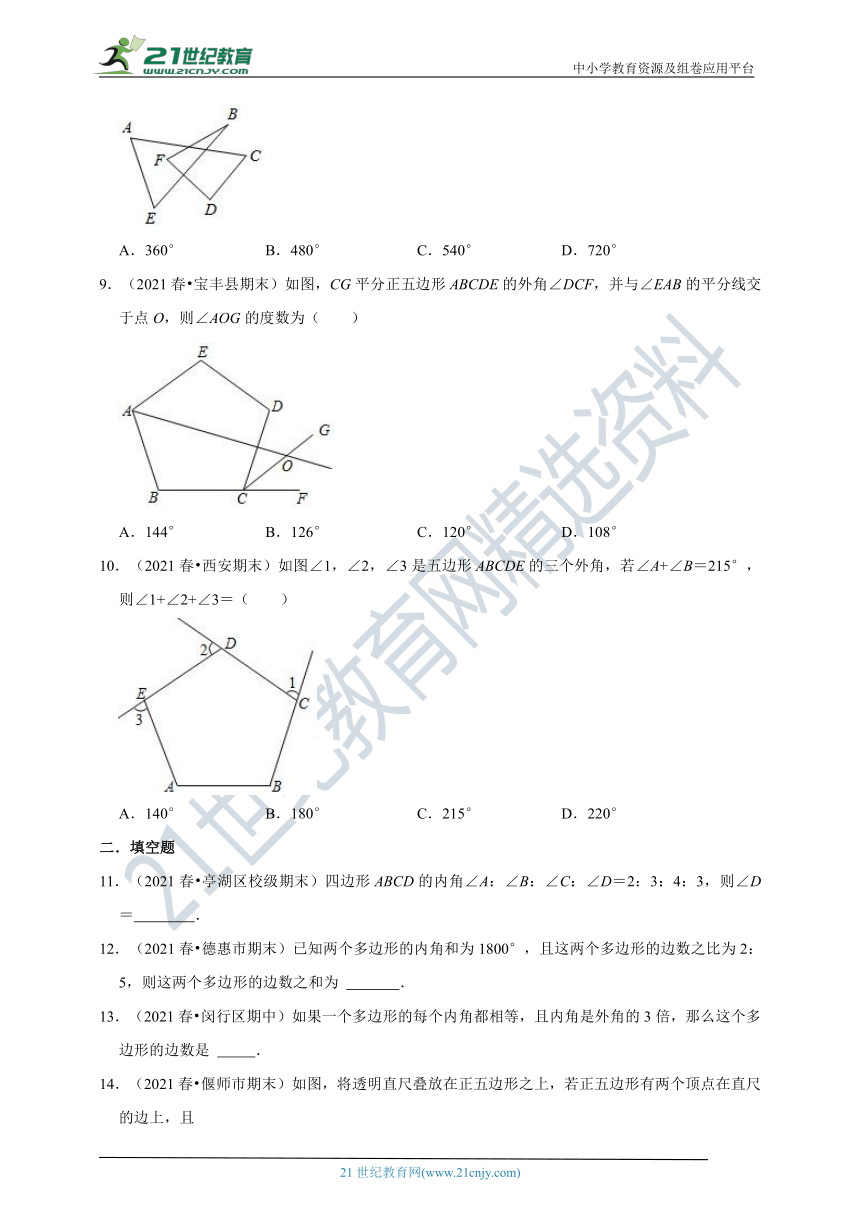
8.(2021?福州模拟)如图,∠A+∠B+∠C+∠D+∠E+∠F的值是( )
A.360°
B.480°
C.540°
D.720°
9.(2021春?宝丰县期末)如图,CG平分正五边形ABCDE的外角∠DCF,并与∠EAB的平分线交于点O,则∠AOG的度数为( )
A.144°
B.126°
C.120°
D.108°
10.(2021春?西安期末)如图∠1,∠2,∠3是五边形ABCDE的三个外角,若∠A+∠B=215°,则∠1+∠2+∠3=( )
A.140°
B.180°
C.215°
D.220°
二.填空题
11.(2021春?亭湖区校级期末)四边形ABCD的内角∠A:∠B:∠C:∠D=2:3:4:3,则∠D=
.
12.(2021春?德惠市期末)已知两个多边形的内角和为1800°,且这两个多边形的边数之比为2:5,则这两个多边形的边数之和为
.
13.(2021春?闵行区期中)如果一个多边形的每个内角都相等,且内角是外角的3倍,那么这个多边形的边数是
.
14.(2021春?偃师市期末)如图,将透明直尺叠放在正五边形之上,若正五边形有两个顶点在直尺的边上,且
有一边与直尺的边垂直.则∠α=
.
15.(2021春?卧龙区期末)如图,五边形ABCDE中,∠A=125°,则∠1+∠2+∠3+∠4的度数是
.
16.(2021春?卢龙县期末)如图,小明从点A出发,前进5m后向右转20°,再前进5m后又向右转20°,这样一直走下去,直到他第一次回到出发点A为止,他所走的路径构成了一个多边形,则这个多边形的内角和是
度.
三.解答题
17.(2021春?长春期末)探究多边形内角和时,我们常把多边形转化成三角形,再根据三角形内角和为180°得出多边形内角和.如图是探究多边形内角和一种方法,请根据图示,完成填空
(1)四边形内角和:4×180°﹣360°=4×180°﹣2×180°=2×180°;
(2)五边形内角和:5×180°﹣360°=5×180°﹣2×180°=
;
(3)六边形内角和:6×180°﹣360°=6×180°﹣2×180°=
;
…
(4)n边形内角和:
=
=
.
18.(2021春?西岗区期末)四边形ABCD中.
(1)如图1,∠A=130°,∠D=80°,∠B比∠C大10°,求∠C的度数;
(2)如图2,若∠A=α,∠D=β,∠ABC的平分线BE交DC于点E,且BE∥AD,求∠C的度数.(用含α、β的式子表示)
19.(2021春?泉州期末)如图,在四边形ABCD中,∠D=90°,E是BC边上一点,EF⊥AE,交CD于点F.
(1)若∠EAD=60°,求∠DFE的度数;
(2)若∠AEB=∠CEF,AE平分∠BAD,试说明:∠B=∠C.
20.(2020秋?朝阳期中)已知n边形的内角和θ=(n﹣2)×180°.
(1)甲同学说,θ能取720°;而乙同学说,θ也能取820°,甲、乙的说法对吗?若对,求出边数n,若不对,说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.
21.(2020春?万州区期末)如图,四边形ABCD中,∠BAD=106°,∠BCD=64°,点M,N分别在AB,BC上,将△BMN沿MN翻折得△FMN,若MF∥AD,FN∥DC.
求(1)∠F的度数;
(2)∠D的度数.
22.(2021春?淅川县期末)将纸片△ABC沿DE折叠使点A落在点A'处
【感知】如图①,点A落在四边形BCDE的边BE上,则∠A与∠1之间的数量关系是
;
【探究】如图②,若点A落在四边形BCDE的内部,则∠A与∠1+∠2之间存在怎样的数量关系?并说明理由.
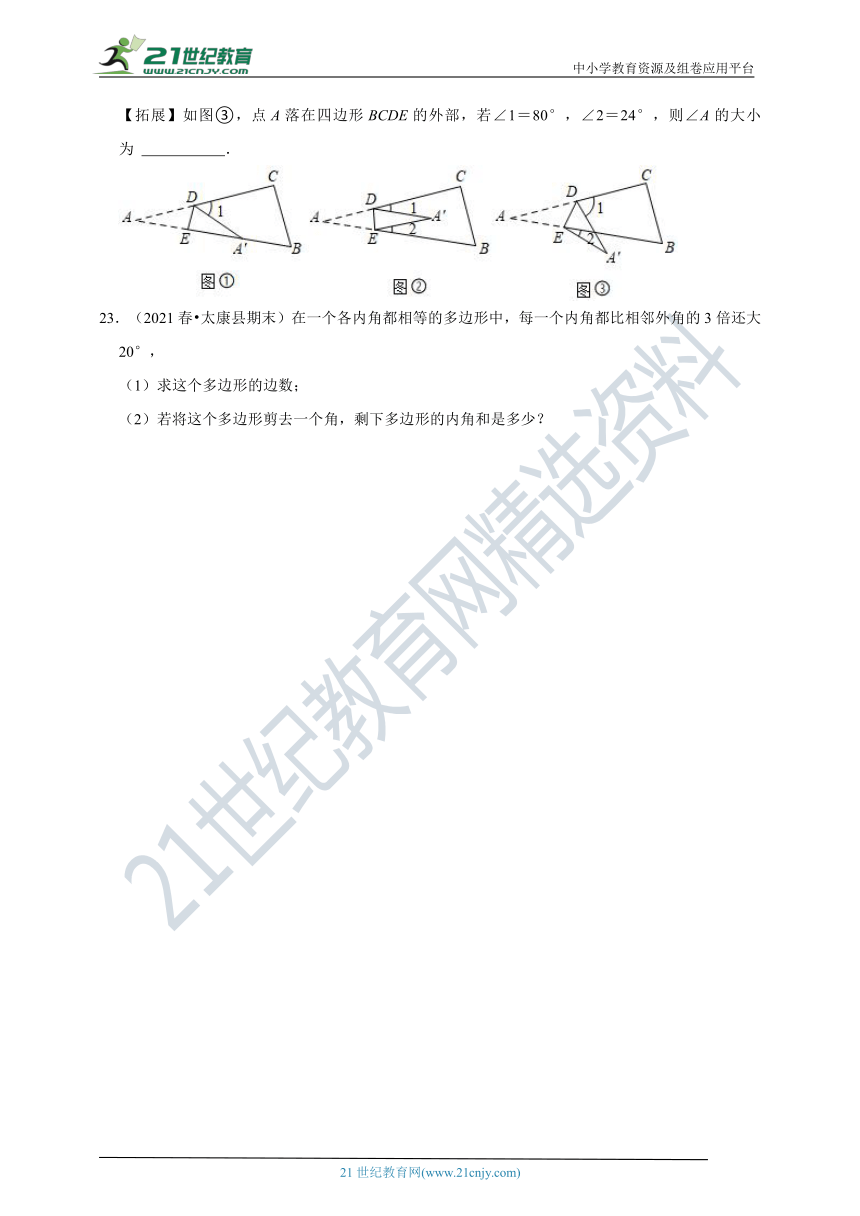
【拓展】如图③,点A落在四边形BCDE的外部,若∠1=80°,∠2=24°,则∠A的大小为
.
23.(2021春?太康县期末)在一个各内角都相等的多边形中,每一个内角都比相邻外角的3倍还大20°,
(1)求这个多边形的边数;
(2)若将这个多边形剪去一个角,剩下多边形的内角和是多少?
答案与解析
一.选择题
1.(2021春?夏津县期末)如果一个多边形的每一个外角都是30°,那么这个多边形的边数是( )
A.12
B.13
C.14
D.15
【解析】解:多边形的边数是:360°÷30°=12.
故选:A.
2.(2021春?凤翔县期末)正多边形的一个内角是120°,则这个正多边形的边数为( )
A.4
B.8
C.6
D.12
【解析】解:设所求正n边形边数为n,
则120°n=(n﹣2)?180°,
解得n=6,
故选:C.
3.(2021春?长春期末)如图,将四边形ABCD去掉一个80°的角得到一个五边形BCDEF,则∠1与∠2的和为( )
A.240°
B.260°
C.280°
D.300°
【解析】解:在△AEF中,∠AEF+∠AFE=180°﹣∠A=100°,
∴∠1+∠2=360°﹣100°=260°,
故选:B.
4.(2021春?洪洞县期末)如果一个正多边形的内角和是外角和的4倍,那么这个正多边形的边数为( )
A.7
B.8
C.9
D.10
【解析】解:设正多边形的边数为n,由题意得:
(n﹣2)?180°=4×360°,
解得:n=10,
故选:D.
5.(2021春?偃师市期末)多边形的边数由3增加到2021时,其外角和的度数( )
A.不能确定
B.减少
C.增加
D.不变
【解析】解:∵任何多边形的外角和都是360°,
∴多边形的边数由3增加到2021时,其外角和的度数不变,
故选:D.
6.(2021春?宛城区期末)小聪为某机器人编制一段程序,如果机器人以0.5m/s的速度在平地上按照图中的步骤行走,那么该机器人从开始到停止所需的时间为( )
A.12s
B.24s
C.48s
D.60s
【解析】解:由题意得,该机器人所经过的路径是一个正多边形,
多边形的边数为:=6,
则所走的路程是:2×6=12(m),
则所用时间是:12÷0.5=24(s).
故选:B.
7.(2021春?渠县校级期末)已知在一个凸多边形中,和一个内角相邻的外角与其余内角度数总和为600°,则这个多边形的边数是( )
A.5
B.6
C.7
D.5或6
【解析】解:设边数为n,这个内角为x度,则0<x<180°根据题意,得
(n﹣2)?180°﹣x+(180°﹣x)=600°,
解得n=4+,
∵n为正整数,
∴60+2x必为180的倍数,
又∵0<x<180°,
∴x=60或150,
∴n=5或6.
故选:D.
8.(2021?福州模拟)如图,∠A+∠B+∠C+∠D+∠E+∠F的值是( )
A.360°
B.480°
C.540°
D.720°
【解析】解:如图,AC、DF与BE分别相交于点M、N,
在四边形NMCD中,∠MND+∠CMN+∠C+∠D=360°,
∵∠CMN=∠A+∠E,∠MND=∠B+∠F,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°,
故选:A.
9.(2021春?宝丰县期末)如图,CG平分正五边形ABCDE的外角∠DCF,并与∠EAB的平分线交于点O,则∠AOG的度数为( )
A.144°
B.126°
C.120°
D.108°
【解析】解:∵任意多边形的外角和等于360°,
∴∠DCF=360°÷5=72°.
∴这个正五边形的每个内角为180°﹣72°=108°.
∴∠B=∠EAB=∠BCD=108°.
又∵AO平分∠EAB,
∴∠OAB=.
又∵CG平分∠DCF,
∴∠DCG=.
∴∠BCO=∠BCD+∠DCG=108°+36°=144°.
∴∠AOC=360°﹣(∠BAO+∠B+∠BCG)=360°﹣(54°+108°+144°)=54°.
∴∠AOG=180°﹣∠AOC=180°﹣54°=126°.
故选:B.
10.(2021春?西安期末)如图∠1,∠2,∠3是五边形ABCDE的三个外角,若∠A+∠B=215°,则∠1+∠2+∠3=( )
A.140°
B.180°
C.215°
D.220°
【解析】解:五边形ABCDE的内角和为(5﹣2)×180°=540°,
∵∠A+∠B=215°,
∴∠AED+∠EDC+∠BCD=540°﹣215°=325°,
又∵∠AED+∠EDC+∠BCD+∠1+∠2+∠3=180°×3=540°,
∴∠1+∠2+∠3=540°﹣325°=215°.
故选:C.
二.填空题
11.(2021春?亭湖区校级期末)四边形ABCD的内角∠A:∠B:∠C:∠D=2:3:4:3,则∠D= 90° .
【解析】解:设∠A=2x°,则∠B=3x°,∠C=4x°,∠D=3x°,
则有2x+2x+4x+3x=360,
所以x=30.
∴∠D=3×30°=90°.
故答案为:90°
12.(2021春?德惠市期末)已知两个多边形的内角和为1800°,且这两个多边形的边数之比为2:5,则这两个多边形的边数之和为
14 .
【解析】解:设两个多边形的边数分别是2x和5x,
则(2x﹣2)?180+(5x﹣2)?180=1800,
解得x=2,
则两个多边形的边数分别为4和10.
边数之和为:4+10=14.
故答案为:14.
13.(2021春?闵行区期中)如果一个多边形的每个内角都相等,且内角是外角的3倍,那么这个多边形的边数是
8 .
【解析】解:设多边形的外角的度数是x,则内角是3x,
则x+3x=180°,
解得:x=45°,
则这个多边形的边数是:360°÷45°=8.
故答案为:8.
14.(2021春?偃师市期末)如图,将透明直尺叠放在正五边形之上,若正五边形有两个顶点在直尺的边上,且
有一边与直尺的边垂直.则∠α= 54° .
【解析】解:如图,
∵正五边形内角和=(5﹣2)×180°=540°,
∴∠A=∠AED=540°÷5=108°,
∵BE∥CD,∠EDC=90°,
∴∠BED=180°﹣90°=90°,
∴∠AEB=∠AED﹣∠BED=108°﹣90°=18°,
在△ABE中∠ABE=180°﹣∠A﹣∠AEB=180°﹣108°﹣18°=54°,
∵BE∥CD,
∴∠α=∠ABE=54°.
故答案为:54°.
15.(2021春?卧龙区期末)如图,五边形ABCDE中,∠A=125°,则∠1+∠2+∠3+∠4的度数是
305° .
【解析】解:如图,
∵∠A=125°,
∴∠5=180°﹣∠A=55°,
∵∠1+∠2+∠3+∠4+∠5=360°,
∴∠1+∠2+∠3+∠4=360°﹣55°=305°.
故答案为:305°.
16.(2021春?卢龙县期末)如图,小明从点A出发,前进5m后向右转20°,再前进5m后又向右转20°,这样一直走下去,直到他第一次回到出发点A为止,他所走的路径构成了一个多边形,则这个多边形的内角和是
2880 度.
【解析】解:由题意知,该多边形为正多边形,
∵多边形的外角和恒为360°,
360÷20=18,
∴该正多边形为正18边形.
这个多边形的内角和为:(18﹣2)×180°=2880°,
故答案为:2880.
三.解答题
17.(2021春?长春期末)探究多边形内角和时,我们常把多边形转化成三角形,再根据三角形内角和为180°得出多边形内角和.如图是探究多边形内角和一种方法,请根据图示,完成填空
(1)四边形内角和:4×180°﹣360°=4×180°﹣2×180°=2×180°;
(2)五边形内角和:5×180°﹣360°=5×180°﹣2×180°= 3×180° ;
(3)六边形内角和:6×180°﹣360°=6×180°﹣2×180°= 4×180° ;
…
(4)n边形内角和: n×180°﹣360° = n×180°﹣2×180° = (n﹣2)×180° .
【解析】解:(2)根据乘法分配律,得5×180°﹣2×180°=(5﹣2)×180°=3×180°.
(3)根据乘法分配律,得6×180°﹣2×180°=(6﹣2)×180°=4×180°.
(4)∵从n边形内部任取一个点,并连接这个点与多边形的各个顶点,可将这个多边形分成n个三角形,
∴多边形内角和:n×180°﹣360°=n×180°﹣2×180°=(n﹣2)×180°.
故答案为:3×180°;4×180°;n×180°﹣360°=n×180°﹣2×180°=(n﹣2)×180°.
18.(2021春?西岗区期末)四边形ABCD中.
(1)如图1,∠A=130°,∠D=80°,∠B比∠C大10°,求∠C的度数;
(2)如图2,若∠A=α,∠D=β,∠ABC的平分线BE交DC于点E,且BE∥AD,求∠C的度数.(用含α、β的式子表示)
【解析】解:(1)∵∠A+∠B+∠C+∠D=360°,∠B比∠C大10°,
∴∠A+∠B+∠B﹣10°+∠D=360°,即130°+∠B+∠B﹣10°+80°=360°,
∴∠B=90°,
∴∠C=∠B﹣10°=80°.
(2)∵BE∥AD,
∴∠BEC=∠D=β,
∠ABE=180°﹣∠A=180°﹣α.
又∵BE平分∠ABC,
∴∠EBC=∠ABE=(180°﹣α),
∴∠C=180°﹣∠EBC﹣∠BEC=180°﹣(180°﹣α)﹣β=90°+α﹣β.
19.(2021春?泉州期末)如图,在四边形ABCD中,∠D=90°,E是BC边上一点,EF⊥AE,交CD于点F.
(1)若∠EAD=60°,求∠DFE的度数;
(2)若∠AEB=∠CEF,AE平分∠BAD,试说明:∠B=∠C.
【解析】(1)解:∵EF⊥AE,
∴∠AEF=90°,
四边形AEFD的内角和是360°,
∵∠D=90°,∠EAD=60°,
∴∠DFE=360°﹣∠D﹣∠EAD﹣∠AEF=120°;
(2)证明:四边形AEFD的内角和是360°,∠AEF=90°,∠D=90°,
∴∠EAD+∠DFE=180°,
∵∠DFE+∠CFE=180°,
∴∠EAD=∠CFE,
∵AE平分∠BAD,
∴∠BAE=∠EAD,
∴∠BAE=∠CFE,
∵∠B+∠BAE+∠AEB=180°,∠C+∠CFE+∠CEF=180°,∠AEB=∠CEF,
∴∠B=∠C.
20.(2020秋?朝阳期中)已知n边形的内角和θ=(n﹣2)×180°.
(1)甲同学说,θ能取720°;而乙同学说,θ也能取820°,甲、乙的说法对吗?若对,求出边数n,若不对,说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.
【解析】解:(1)甲对,乙不对.
理由:∵当θ取720°时,720°=(n﹣2)×180°,
解得θ=6;
当θ取820°时,820°=(n﹣2)×180°,
解得θ=;
∵n为整数,
∴θ不能取820°;
(2)依题意得,
(n﹣2)×180°+360°=(n+x﹣2)×180°,
解得x=2.
21.(2020春?万州区期末)如图,四边形ABCD中,∠BAD=106°,∠BCD=64°,点M,N分别在AB,BC上,将△BMN沿MN翻折得△FMN,若MF∥AD,FN∥DC.
求(1)∠F的度数;
(2)∠D的度数.
【解析】解:(1)∵MF∥AD,FN∥DC,∠BAD=106°,∠BCD=64°,
∴∠BMF=106°,∠FNB=64°,
∵将△BMN沿MN翻折,得△FMN,
∴∠FMN=∠BMN=53°,∠FNM=∠MNB=32°,
∴∠F=∠B=180°﹣53°﹣32°=95°;
(2)∠F=∠B=95°,
∠D=360°﹣106°﹣64°﹣95°=95°.
22.(2021春?淅川县期末)将纸片△ABC沿DE折叠使点A落在点A'处
【感知】如图①,点A落在四边形BCDE的边BE上,则∠A与∠1之间的数量关系是
∠1=2∠A ;
【探究】如图②,若点A落在四边形BCDE的内部,则∠A与∠1+∠2之间存在怎样的数量关系?并说明理由.
【拓展】如图③,点A落在四边形BCDE的外部,若∠1=80°,∠2=24°,则∠A的大小为
28° .
【解析】解:(1)如图①,∠1=2∠A.
理由如下:由折叠知识可得:∠EA′D=∠A;
∵∠1=∠A+∠EA′D,
∴∠1=2∠A.
(2)如图②,2∠A=∠1+∠2.
理由如下:∵∠1+∠A′DA+∠2+∠A′EA=360°,
∠A+∠A′+∠A′DA+∠A′EA=360°,
∴∠A′+∠A=∠1+∠2,
由折叠知识可得:∠A=∠A′,
∴2∠A=∠1+∠2.
(3)如图③,
∵∠1=∠DFA+∠A,∠DFA=∠A′+∠2,
∴∠1=∠A+∠A′+∠2=2∠A+∠2,
∴2∠A=∠1﹣∠2=56°,
解得∠A=28°.
故答案为:∠1=2∠A;28°.
23.(2021春?太康县期末)在一个各内角都相等的多边形中,每一个内角都比相邻外角的3倍还大20°,
(1)求这个多边形的边数;
(2)若将这个多边形剪去一个角,剩下多边形的内角和是多少?
【解析】解:(1)设多边形的一个外角为α,则与其相邻的内角等于3α+20°,
由题意,得(3α+20)+α=180°,解得α=40°.
即多边形的每个外角为40°.
又∵多边形的外角和为360°,
∴多边形的外角个数==9.
∴多边形的边数=9,
答:这个多边形的边数是9;
(2)因为剪掉一个角以后,多边形的边数可能增加了1条,也可能减少了1条,或者不变,
当截线为经过对角2个顶点的直线时,多边形的边数减少了1条边,内角和=(9﹣2﹣1)×180°=1080°;
当截线为经过多边形一组对边的直线时,多边形的边数不变,内角和=(9﹣2)×180°=1260°;
当截线为只经过正方形一组邻边的一条直线时,多边形的边数增加一条边,内角和=(9﹣2+1)×180°=1440°.
答:将这个多边形剪去一个角,剩下多边形的内角和是1080°或1260°或1440°.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
人教版八年级上
11.3多边形及其内角和同步练习
一.选择题
1.(2021春?夏津县期末)如果一个多边形的每一个外角都是30°,那么这个多边形的边数是( )
A.12
B.13
C.14
D.15
2.(2021春?凤翔县期末)正多边形的一个内角是120°,则这个正多边形的边数为( )
A.4
B.8
C.6
D.12
3.(2021春?长春期末)如图,将四边形ABCD去掉一个80°的角得到一个五边形BCDEF,则∠1与∠2的和为( )
A.240°
B.260°
C.280°
D.300°
4.(2021春?洪洞县期末)如果一个正多边形的内角和是外角和的4倍,那么这个正多边形的边数为( )
A.7
B.8
C.9
D.10
5.(2021春?偃师市期末)多边形的边数由3增加到2021时,其外角和的度数( )
A.不能确定
B.减少
C.增加
D.不变
6.(2021春?宛城区期末)小聪为某机器人编制一段程序,如果机器人以0.5m/s的速度在平地上按照图中的步骤行走,那么该机器人从开始到停止所需的时间为( )
A.12s
B.24s
C.48s
D.60s
7.(2021春?渠县校级期末)已知在一个凸多边形中,和一个内角相邻的外角与其余内角度数总和为600°,则这个多边形的边数是( )
A.5
B.6
C.7
D.5或6
8.(2021?福州模拟)如图,∠A+∠B+∠C+∠D+∠E+∠F的值是( )
A.360°
B.480°
C.540°
D.720°
9.(2021春?宝丰县期末)如图,CG平分正五边形ABCDE的外角∠DCF,并与∠EAB的平分线交于点O,则∠AOG的度数为( )
A.144°
B.126°
C.120°
D.108°
10.(2021春?西安期末)如图∠1,∠2,∠3是五边形ABCDE的三个外角,若∠A+∠B=215°,则∠1+∠2+∠3=( )
A.140°
B.180°
C.215°
D.220°
二.填空题
11.(2021春?亭湖区校级期末)四边形ABCD的内角∠A:∠B:∠C:∠D=2:3:4:3,则∠D=
.
12.(2021春?德惠市期末)已知两个多边形的内角和为1800°,且这两个多边形的边数之比为2:5,则这两个多边形的边数之和为
.
13.(2021春?闵行区期中)如果一个多边形的每个内角都相等,且内角是外角的3倍,那么这个多边形的边数是
.
14.(2021春?偃师市期末)如图,将透明直尺叠放在正五边形之上,若正五边形有两个顶点在直尺的边上,且
有一边与直尺的边垂直.则∠α=
.
15.(2021春?卧龙区期末)如图,五边形ABCDE中,∠A=125°,则∠1+∠2+∠3+∠4的度数是
.
16.(2021春?卢龙县期末)如图,小明从点A出发,前进5m后向右转20°,再前进5m后又向右转20°,这样一直走下去,直到他第一次回到出发点A为止,他所走的路径构成了一个多边形,则这个多边形的内角和是
度.
三.解答题
17.(2021春?长春期末)探究多边形内角和时,我们常把多边形转化成三角形,再根据三角形内角和为180°得出多边形内角和.如图是探究多边形内角和一种方法,请根据图示,完成填空
(1)四边形内角和:4×180°﹣360°=4×180°﹣2×180°=2×180°;
(2)五边形内角和:5×180°﹣360°=5×180°﹣2×180°=
;
(3)六边形内角和:6×180°﹣360°=6×180°﹣2×180°=
;
…
(4)n边形内角和:
=
=
.
18.(2021春?西岗区期末)四边形ABCD中.
(1)如图1,∠A=130°,∠D=80°,∠B比∠C大10°,求∠C的度数;
(2)如图2,若∠A=α,∠D=β,∠ABC的平分线BE交DC于点E,且BE∥AD,求∠C的度数.(用含α、β的式子表示)
19.(2021春?泉州期末)如图,在四边形ABCD中,∠D=90°,E是BC边上一点,EF⊥AE,交CD于点F.
(1)若∠EAD=60°,求∠DFE的度数;
(2)若∠AEB=∠CEF,AE平分∠BAD,试说明:∠B=∠C.
20.(2020秋?朝阳期中)已知n边形的内角和θ=(n﹣2)×180°.
(1)甲同学说,θ能取720°;而乙同学说,θ也能取820°,甲、乙的说法对吗?若对,求出边数n,若不对,说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.
21.(2020春?万州区期末)如图,四边形ABCD中,∠BAD=106°,∠BCD=64°,点M,N分别在AB,BC上,将△BMN沿MN翻折得△FMN,若MF∥AD,FN∥DC.
求(1)∠F的度数;
(2)∠D的度数.
22.(2021春?淅川县期末)将纸片△ABC沿DE折叠使点A落在点A'处
【感知】如图①,点A落在四边形BCDE的边BE上,则∠A与∠1之间的数量关系是
;
【探究】如图②,若点A落在四边形BCDE的内部,则∠A与∠1+∠2之间存在怎样的数量关系?并说明理由.
【拓展】如图③,点A落在四边形BCDE的外部,若∠1=80°,∠2=24°,则∠A的大小为
.
23.(2021春?太康县期末)在一个各内角都相等的多边形中,每一个内角都比相邻外角的3倍还大20°,
(1)求这个多边形的边数;
(2)若将这个多边形剪去一个角,剩下多边形的内角和是多少?
答案与解析
一.选择题
1.(2021春?夏津县期末)如果一个多边形的每一个外角都是30°,那么这个多边形的边数是( )
A.12
B.13
C.14
D.15
【解析】解:多边形的边数是:360°÷30°=12.
故选:A.
2.(2021春?凤翔县期末)正多边形的一个内角是120°,则这个正多边形的边数为( )
A.4
B.8
C.6
D.12
【解析】解:设所求正n边形边数为n,
则120°n=(n﹣2)?180°,
解得n=6,
故选:C.
3.(2021春?长春期末)如图,将四边形ABCD去掉一个80°的角得到一个五边形BCDEF,则∠1与∠2的和为( )
A.240°
B.260°
C.280°
D.300°
【解析】解:在△AEF中,∠AEF+∠AFE=180°﹣∠A=100°,
∴∠1+∠2=360°﹣100°=260°,
故选:B.
4.(2021春?洪洞县期末)如果一个正多边形的内角和是外角和的4倍,那么这个正多边形的边数为( )
A.7
B.8
C.9
D.10
【解析】解:设正多边形的边数为n,由题意得:
(n﹣2)?180°=4×360°,
解得:n=10,
故选:D.
5.(2021春?偃师市期末)多边形的边数由3增加到2021时,其外角和的度数( )
A.不能确定
B.减少
C.增加
D.不变
【解析】解:∵任何多边形的外角和都是360°,
∴多边形的边数由3增加到2021时,其外角和的度数不变,
故选:D.
6.(2021春?宛城区期末)小聪为某机器人编制一段程序,如果机器人以0.5m/s的速度在平地上按照图中的步骤行走,那么该机器人从开始到停止所需的时间为( )
A.12s
B.24s
C.48s
D.60s
【解析】解:由题意得,该机器人所经过的路径是一个正多边形,
多边形的边数为:=6,
则所走的路程是:2×6=12(m),
则所用时间是:12÷0.5=24(s).
故选:B.
7.(2021春?渠县校级期末)已知在一个凸多边形中,和一个内角相邻的外角与其余内角度数总和为600°,则这个多边形的边数是( )
A.5
B.6
C.7
D.5或6
【解析】解:设边数为n,这个内角为x度,则0<x<180°根据题意,得
(n﹣2)?180°﹣x+(180°﹣x)=600°,
解得n=4+,
∵n为正整数,
∴60+2x必为180的倍数,
又∵0<x<180°,
∴x=60或150,
∴n=5或6.
故选:D.
8.(2021?福州模拟)如图,∠A+∠B+∠C+∠D+∠E+∠F的值是( )
A.360°
B.480°
C.540°
D.720°
【解析】解:如图,AC、DF与BE分别相交于点M、N,
在四边形NMCD中,∠MND+∠CMN+∠C+∠D=360°,
∵∠CMN=∠A+∠E,∠MND=∠B+∠F,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°,
故选:A.
9.(2021春?宝丰县期末)如图,CG平分正五边形ABCDE的外角∠DCF,并与∠EAB的平分线交于点O,则∠AOG的度数为( )
A.144°
B.126°
C.120°
D.108°
【解析】解:∵任意多边形的外角和等于360°,
∴∠DCF=360°÷5=72°.
∴这个正五边形的每个内角为180°﹣72°=108°.
∴∠B=∠EAB=∠BCD=108°.
又∵AO平分∠EAB,
∴∠OAB=.
又∵CG平分∠DCF,
∴∠DCG=.
∴∠BCO=∠BCD+∠DCG=108°+36°=144°.
∴∠AOC=360°﹣(∠BAO+∠B+∠BCG)=360°﹣(54°+108°+144°)=54°.
∴∠AOG=180°﹣∠AOC=180°﹣54°=126°.
故选:B.
10.(2021春?西安期末)如图∠1,∠2,∠3是五边形ABCDE的三个外角,若∠A+∠B=215°,则∠1+∠2+∠3=( )
A.140°
B.180°
C.215°
D.220°
【解析】解:五边形ABCDE的内角和为(5﹣2)×180°=540°,
∵∠A+∠B=215°,
∴∠AED+∠EDC+∠BCD=540°﹣215°=325°,
又∵∠AED+∠EDC+∠BCD+∠1+∠2+∠3=180°×3=540°,
∴∠1+∠2+∠3=540°﹣325°=215°.
故选:C.
二.填空题
11.(2021春?亭湖区校级期末)四边形ABCD的内角∠A:∠B:∠C:∠D=2:3:4:3,则∠D= 90° .
【解析】解:设∠A=2x°,则∠B=3x°,∠C=4x°,∠D=3x°,
则有2x+2x+4x+3x=360,
所以x=30.
∴∠D=3×30°=90°.
故答案为:90°
12.(2021春?德惠市期末)已知两个多边形的内角和为1800°,且这两个多边形的边数之比为2:5,则这两个多边形的边数之和为
14 .
【解析】解:设两个多边形的边数分别是2x和5x,
则(2x﹣2)?180+(5x﹣2)?180=1800,
解得x=2,
则两个多边形的边数分别为4和10.
边数之和为:4+10=14.
故答案为:14.
13.(2021春?闵行区期中)如果一个多边形的每个内角都相等,且内角是外角的3倍,那么这个多边形的边数是
8 .
【解析】解:设多边形的外角的度数是x,则内角是3x,
则x+3x=180°,
解得:x=45°,
则这个多边形的边数是:360°÷45°=8.
故答案为:8.
14.(2021春?偃师市期末)如图,将透明直尺叠放在正五边形之上,若正五边形有两个顶点在直尺的边上,且
有一边与直尺的边垂直.则∠α= 54° .
【解析】解:如图,
∵正五边形内角和=(5﹣2)×180°=540°,
∴∠A=∠AED=540°÷5=108°,
∵BE∥CD,∠EDC=90°,
∴∠BED=180°﹣90°=90°,
∴∠AEB=∠AED﹣∠BED=108°﹣90°=18°,
在△ABE中∠ABE=180°﹣∠A﹣∠AEB=180°﹣108°﹣18°=54°,
∵BE∥CD,
∴∠α=∠ABE=54°.
故答案为:54°.
15.(2021春?卧龙区期末)如图,五边形ABCDE中,∠A=125°,则∠1+∠2+∠3+∠4的度数是
305° .
【解析】解:如图,
∵∠A=125°,
∴∠5=180°﹣∠A=55°,
∵∠1+∠2+∠3+∠4+∠5=360°,
∴∠1+∠2+∠3+∠4=360°﹣55°=305°.
故答案为:305°.
16.(2021春?卢龙县期末)如图,小明从点A出发,前进5m后向右转20°,再前进5m后又向右转20°,这样一直走下去,直到他第一次回到出发点A为止,他所走的路径构成了一个多边形,则这个多边形的内角和是
2880 度.
【解析】解:由题意知,该多边形为正多边形,
∵多边形的外角和恒为360°,
360÷20=18,
∴该正多边形为正18边形.
这个多边形的内角和为:(18﹣2)×180°=2880°,
故答案为:2880.
三.解答题
17.(2021春?长春期末)探究多边形内角和时,我们常把多边形转化成三角形,再根据三角形内角和为180°得出多边形内角和.如图是探究多边形内角和一种方法,请根据图示,完成填空
(1)四边形内角和:4×180°﹣360°=4×180°﹣2×180°=2×180°;
(2)五边形内角和:5×180°﹣360°=5×180°﹣2×180°= 3×180° ;
(3)六边形内角和:6×180°﹣360°=6×180°﹣2×180°= 4×180° ;
…
(4)n边形内角和: n×180°﹣360° = n×180°﹣2×180° = (n﹣2)×180° .
【解析】解:(2)根据乘法分配律,得5×180°﹣2×180°=(5﹣2)×180°=3×180°.
(3)根据乘法分配律,得6×180°﹣2×180°=(6﹣2)×180°=4×180°.
(4)∵从n边形内部任取一个点,并连接这个点与多边形的各个顶点,可将这个多边形分成n个三角形,
∴多边形内角和:n×180°﹣360°=n×180°﹣2×180°=(n﹣2)×180°.
故答案为:3×180°;4×180°;n×180°﹣360°=n×180°﹣2×180°=(n﹣2)×180°.
18.(2021春?西岗区期末)四边形ABCD中.
(1)如图1,∠A=130°,∠D=80°,∠B比∠C大10°,求∠C的度数;
(2)如图2,若∠A=α,∠D=β,∠ABC的平分线BE交DC于点E,且BE∥AD,求∠C的度数.(用含α、β的式子表示)
【解析】解:(1)∵∠A+∠B+∠C+∠D=360°,∠B比∠C大10°,
∴∠A+∠B+∠B﹣10°+∠D=360°,即130°+∠B+∠B﹣10°+80°=360°,
∴∠B=90°,
∴∠C=∠B﹣10°=80°.
(2)∵BE∥AD,
∴∠BEC=∠D=β,
∠ABE=180°﹣∠A=180°﹣α.
又∵BE平分∠ABC,
∴∠EBC=∠ABE=(180°﹣α),
∴∠C=180°﹣∠EBC﹣∠BEC=180°﹣(180°﹣α)﹣β=90°+α﹣β.
19.(2021春?泉州期末)如图,在四边形ABCD中,∠D=90°,E是BC边上一点,EF⊥AE,交CD于点F.
(1)若∠EAD=60°,求∠DFE的度数;
(2)若∠AEB=∠CEF,AE平分∠BAD,试说明:∠B=∠C.
【解析】(1)解:∵EF⊥AE,
∴∠AEF=90°,
四边形AEFD的内角和是360°,
∵∠D=90°,∠EAD=60°,
∴∠DFE=360°﹣∠D﹣∠EAD﹣∠AEF=120°;
(2)证明:四边形AEFD的内角和是360°,∠AEF=90°,∠D=90°,
∴∠EAD+∠DFE=180°,
∵∠DFE+∠CFE=180°,
∴∠EAD=∠CFE,
∵AE平分∠BAD,
∴∠BAE=∠EAD,
∴∠BAE=∠CFE,
∵∠B+∠BAE+∠AEB=180°,∠C+∠CFE+∠CEF=180°,∠AEB=∠CEF,
∴∠B=∠C.
20.(2020秋?朝阳期中)已知n边形的内角和θ=(n﹣2)×180°.
(1)甲同学说,θ能取720°;而乙同学说,θ也能取820°,甲、乙的说法对吗?若对,求出边数n,若不对,说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.
【解析】解:(1)甲对,乙不对.
理由:∵当θ取720°时,720°=(n﹣2)×180°,
解得θ=6;
当θ取820°时,820°=(n﹣2)×180°,
解得θ=;
∵n为整数,
∴θ不能取820°;
(2)依题意得,
(n﹣2)×180°+360°=(n+x﹣2)×180°,
解得x=2.
21.(2020春?万州区期末)如图,四边形ABCD中,∠BAD=106°,∠BCD=64°,点M,N分别在AB,BC上,将△BMN沿MN翻折得△FMN,若MF∥AD,FN∥DC.
求(1)∠F的度数;
(2)∠D的度数.
【解析】解:(1)∵MF∥AD,FN∥DC,∠BAD=106°,∠BCD=64°,
∴∠BMF=106°,∠FNB=64°,
∵将△BMN沿MN翻折,得△FMN,
∴∠FMN=∠BMN=53°,∠FNM=∠MNB=32°,
∴∠F=∠B=180°﹣53°﹣32°=95°;
(2)∠F=∠B=95°,
∠D=360°﹣106°﹣64°﹣95°=95°.
22.(2021春?淅川县期末)将纸片△ABC沿DE折叠使点A落在点A'处
【感知】如图①,点A落在四边形BCDE的边BE上,则∠A与∠1之间的数量关系是
∠1=2∠A ;
【探究】如图②,若点A落在四边形BCDE的内部,则∠A与∠1+∠2之间存在怎样的数量关系?并说明理由.
【拓展】如图③,点A落在四边形BCDE的外部,若∠1=80°,∠2=24°,则∠A的大小为
28° .
【解析】解:(1)如图①,∠1=2∠A.
理由如下:由折叠知识可得:∠EA′D=∠A;
∵∠1=∠A+∠EA′D,
∴∠1=2∠A.
(2)如图②,2∠A=∠1+∠2.
理由如下:∵∠1+∠A′DA+∠2+∠A′EA=360°,
∠A+∠A′+∠A′DA+∠A′EA=360°,
∴∠A′+∠A=∠1+∠2,
由折叠知识可得:∠A=∠A′,
∴2∠A=∠1+∠2.
(3)如图③,
∵∠1=∠DFA+∠A,∠DFA=∠A′+∠2,
∴∠1=∠A+∠A′+∠2=2∠A+∠2,
∴2∠A=∠1﹣∠2=56°,
解得∠A=28°.
故答案为:∠1=2∠A;28°.
23.(2021春?太康县期末)在一个各内角都相等的多边形中,每一个内角都比相邻外角的3倍还大20°,
(1)求这个多边形的边数;
(2)若将这个多边形剪去一个角,剩下多边形的内角和是多少?
【解析】解:(1)设多边形的一个外角为α,则与其相邻的内角等于3α+20°,
由题意,得(3α+20)+α=180°,解得α=40°.
即多边形的每个外角为40°.
又∵多边形的外角和为360°,
∴多边形的外角个数==9.
∴多边形的边数=9,
答:这个多边形的边数是9;
(2)因为剪掉一个角以后,多边形的边数可能增加了1条,也可能减少了1条,或者不变,
当截线为经过对角2个顶点的直线时,多边形的边数减少了1条边,内角和=(9﹣2﹣1)×180°=1080°;
当截线为经过多边形一组对边的直线时,多边形的边数不变,内角和=(9﹣2)×180°=1260°;
当截线为只经过正方形一组邻边的一条直线时,多边形的边数增加一条边,内角和=(9﹣2+1)×180°=1440°.
答:将这个多边形剪去一个角,剩下多边形的内角和是1080°或1260°或1440°.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
